Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».
Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]
- Стоимость занятий
- Видеокурсы подготовки к ЕГЭ-2021
- Группа Вконтакте
- Преимущества
- Педагогический стаж
- Собственная методика
- Гарантированный результат
- Индивидуальная работа
- В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины сторон AB и CD, равна одному метру?
- В выпуклом четырёхугольнике KLMN длина отрезка соединяющего середины диагоналей равна 1м?
- Основания трапеции равны 17 и 4 а боковые стороны 12 и 5 см найдите длину отрезка соединяющего середины оснований?
- В выпуклом четырехугольнике отрезки, соединяющие середины противоположных сторон равны?
- АЙТИ ДЛИНЫ ОТРЕЗКОВ СОЕДИНЯЮЩИХ СЕРЕДИНЫ СТОРОН ТРАПЕЦИИ С РАВНЫМИ ДИАГОНАЛЯМИ ЕСЛИ ЕЁ ОСНОВАНИЯ = 7 СМ И 9 СМ, А ВЫСОТА = 8 СМ?
- Доказать что отрезки соединяющие середины противоположных сторон равнобедренной трапеции взаимно перпендикулярны?
- В выпуклом четырехугольнике ABCT длина отрезка , соединяющего середины сторон AB и СТ равна одному метру?
- Высота равнобедренной трапеции, проведенная из вершины меньшего основания, делит большее основание на части длиной 3 см и 8 см?
- Основание трапеции 15 и 35 см ?
- В четырехугольнике отрезки соединяющие середины противоположных сторон равны?
- Верно ли, что длина стороны треугольника в два раза больше длины отрезка, соединяющего середины двух других сторон?
- Г. И. Ковалева Итоговое повторение курса планиметрии с привлечением метода ключевой задачи
- Главная > Документ
- 📺 Видео
Стоимость занятий
Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.
Видеокурсы подготовки к ЕГЭ-2021
Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.
Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.
Видео:№43. Докажите, что середины сторон пространственного четырехугольника* являютсяСкачать

Группа Вконтакте
В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.
Видео:Длина отрезка | Геометрия 7-9 класс #8 | ИнфоурокСкачать

Преимущества
Педагогический стаж
Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.
Собственная методика
За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.
Гарантированный результат
За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.
Индивидуальная работа
Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.
Видео:Длина отрезкаСкачать

В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины сторон AB и CD, равна одному метру?
Геометрия | 5 — 9 классы
В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины сторон AB и CD, равна одному метру.
Прямые BC и AD перпендикулярны.
Найдите длину отрезка, соединяющего середины диагоналей AC и BD.
Обозначены : M — середина AB ; N — середина BD ; K — середина CD ; P — середина AC ;
В треугольнике ABC MP — средняя линия, то есть MP II BC ; MP = BC / 2 ;
В треугольнике BDC NK — средняя линия, то есть NK II BC ; NK = BC / 2 ;
В треугольнике ABD MN — средняя линия, то есть MN II AD ; MN = AD / 2 ;
В треугольнике ADC KP — средняя линия, то есть KP II AD ; KP = AD / 2 ;
Легко видеть, что MNKP — прямоугольник.
У прямоугольника диагонали равны, то есть PN = MK ;
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

В выпуклом четырёхугольнике KLMN длина отрезка соединяющего середины диагоналей равна 1м?
В выпуклом четырёхугольнике KLMN длина отрезка соединяющего середины диагоналей равна 1м.
Прямые LM и KN перпендикулярны.
Найти длину отрезка соединяющего середины сторон KL и MN.
Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Основания трапеции равны 17 и 4 а боковые стороны 12 и 5 см найдите длину отрезка соединяющего середины оснований?
Основания трапеции равны 17 и 4 а боковые стороны 12 и 5 см найдите длину отрезка соединяющего середины оснований.
Видео:7 класс, 7 урок, Длина отрезкаСкачать

В выпуклом четырехугольнике отрезки, соединяющие середины противоположных сторон равны?
В выпуклом четырехугольнике отрезки, соединяющие середины противоположных сторон равны.
Докажите, что диагонали четырехугольника перпендикулярны.
Видео:ЕГЭ Математика Задание 6#27845Скачать

АЙТИ ДЛИНЫ ОТРЕЗКОВ СОЕДИНЯЮЩИХ СЕРЕДИНЫ СТОРОН ТРАПЕЦИИ С РАВНЫМИ ДИАГОНАЛЯМИ ЕСЛИ ЕЁ ОСНОВАНИЯ = 7 СМ И 9 СМ, А ВЫСОТА = 8 СМ?
АЙТИ ДЛИНЫ ОТРЕЗКОВ СОЕДИНЯЮЩИХ СЕРЕДИНЫ СТОРОН ТРАПЕЦИИ С РАВНЫМИ ДИАГОНАЛЯМИ ЕСЛИ ЕЁ ОСНОВАНИЯ = 7 СМ И 9 СМ, А ВЫСОТА = 8 СМ.
Видео:Планиметрия_03_05Скачать

Доказать что отрезки соединяющие середины противоположных сторон равнобедренной трапеции взаимно перпендикулярны?
Доказать что отрезки соединяющие середины противоположных сторон равнобедренной трапеции взаимно перпендикулярны.
Видео:№569. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллеленСкачать
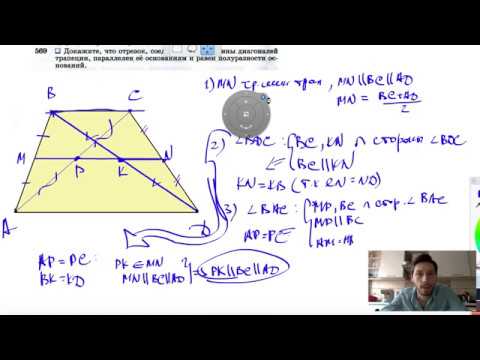
В выпуклом четырехугольнике ABCT длина отрезка , соединяющего середины сторон AB и СТ равна одному метру?
В выпуклом четырехугольнике ABCT длина отрезка , соединяющего середины сторон AB и СТ равна одному метру.
Прямые BC и AT перпендикулярны.
Найдите длину отрезка , соединяющего середины.
Диагоналей АС и ВТ.
С полным оформлением и решением.
Видео:Геометрия 7 класс (Урок№4 - Измерение отрезков.)Скачать

Высота равнобедренной трапеции, проведенная из вершины меньшего основания, делит большее основание на части длиной 3 см и 8 см?
Высота равнобедренной трапеции, проведенная из вершины меньшего основания, делит большее основание на части длиной 3 см и 8 см.
Найдите сумму длины отрезка, соединяющего середины боковых сторон, и отрезка, соединяющего середины диагоналей.
Видео:Задание 16 ЕГЭ 2020 по математике (профиль). Геометрия. Параллелограмм (часть 6).Скачать

Основание трапеции 15 и 35 см ?
Основание трапеции 15 и 35 см .
Найдите длину отрезка соединяющего середины диагоналей трапеции.
Видео:Отрезок. Длина отрезка. Треугольник | Математика 5 класс #2 | ИнфоурокСкачать

В четырехугольнике отрезки соединяющие середины противоположных сторон равны?
В четырехугольнике отрезки соединяющие середины противоположных сторон равны.
Докажите что угол между диагоналями этого четырехугольника равен 90.
Видео:Геометрия Диагонали выпуклого четырехугольника ABCD перпендикулярны. Через середины сторон AB и ADСкачать

Верно ли, что длина стороны треугольника в два раза больше длины отрезка, соединяющего середины двух других сторон?
Верно ли, что длина стороны треугольника в два раза больше длины отрезка, соединяющего середины двух других сторон?
На этой странице находится ответ на вопрос В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины сторон AB и CD, равна одному метру?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.
Угол САВ = 180 — 94 = 86 * Треугольник АВС — равнобедренный следовательно угол А равен углу В следовательно угол В = углу А = 86. Сумма углов треугольника равна 180 * . Следовательно угол АСВ = 180 — А — В = 180 — 86 — 86 = 8. Угол АСВ = 8 * Угол ..
Нехай кут А і С — кути при основі, тоді кут А = С = 180 — 94 = 86градусів Кут В — протилежний до основи, кут В = 180 — 86 * 2 = 8 Зовнішній кут при вершині В = 180 — 8 = 172 градуси В — дь : 172.
Они будут н л , они равны а ост. Смежные их сумма равна 180° = > 180° — 43° =.
Пусть биссектриса х. Стороны треугольника a, b, c a + b + c = 36 (периметр треугольника) a + b + c + 2x = 24 + 30 (периметры двух треугольников, на которые разбивает биссектриса данный треугольник) 36 + 2х = 54 2х = 54 — 36 2х = 18 х = 18 : 2 х = 9 ..
Решение в прикрепленном файле.
Трапеция прямоугольная = > два угла, прилежащие к одной боковой стороне, по 90°, Сумма углов, прилежащих к другой боковой стороне, = 180° 180° — 100° = 80° четвертый угол. Ответ : 90°, 90°, 80° и 100°.
Видео:Теорема Вариньона. Середины сторон четырёхугольника.Скачать
Г. И. Ковалева Итоговое повторение курса планиметрии с привлечением метода ключевой задачи
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Треугольник, образованный основаниями высот
данного остроугольного треугольника
Ключевая задача. АА 1 , ВВ 1 , СС 1 – высоты остроугольного треугольника АВС . Докажите, что а) треугольники АА 1 С и ВВ 1 С подобны; б) треугольники АВС и А 1 В 1 С подобны и 
Д о к а з а т е л ь с т в о. Треугольники АА 1 С и ВВ 1 С подобны по двум углам.
Из этого следует, что 




Задача 1. АА 1 , ВВ 1 , СС 1 – высоты остроугольного треугольника АВС . Докажите, что АА 1 , ВВ 1 , СС 1 – биссектрисы углов треугольника А 1 В 1 С 1 .
Д о к а з а т е л ь с т в о. Треугольники АВС и А 1 В 1 С подобны, следовательно, 
Треугольники АВС и А 1 ВС 1 подобны, следовательно, 


Задача 2. АА 1 , ВВ 1 , СС 1 – высоты остроугольного треугольника АВС . Докажите, что 
Д о к а з а т е л ь с т в о. 



Имеем 



Задача 3. АА 1 , ВВ 1 , СС 1 – высоты остроугольного треугольника АВС . Докажите, что отношение периметров треугольников А 1 В 1 С 1 и АВС равно 
Р е ш е н и е. Так как 





Найдем площади треугольников АОВ , ВОС и АОС .

Анологично, 


Приравнивая площади, получим 
Задача 4. Отрезки, соединяющие основания высот остроугольного треугольника, равны 8, 15 и 17. Найдите стороны треугольника.
Р е ш е н и е. Так как 






Используя формулу понижения степени 



Рассуждая аналогично, можно найти сторону ВС . 


О т в е т: 


Задачи для самостоятельного решения
1. Высота АН и СК остроугольного треугольника АВС пересекаются в точке D , причем 


2. В остроугольном треугольнике АВС проведены высоты АА 1 , ВВ 1 , и СС 1 . Докажите, что 
3. Длина основания равнобедренного треугольника равна 12, а боковой стороны – 18. К боковым сторонам треугольника проведены высоты. Найдите длину отрезка с концами в основаниях высот.
О т в е т: 
4. В остроугольном треугольнике АВС проведены высоты СС 1 и АА 1 . Известно, что 

О т в е т: 
5. В остроугольном треугольнике АВС 
О т в е т: 
Четырехугольник, вершины которого
являются серединами сторон данного четырехугольника
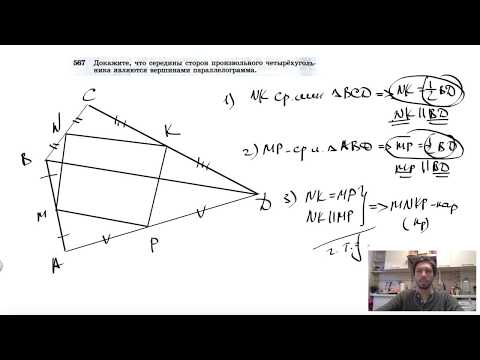
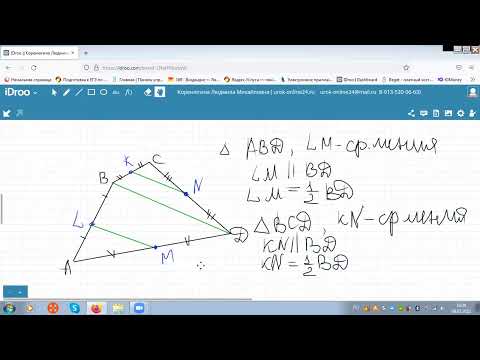
Ключевая задача. Середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Д о к а з а т е л ь с т в о. Пусть ABCD – выпуклый четырехугольник.
M , N , P , K – середины сторон АВ, ВС, CD и А D соответственно.
Отрезок MN параллелен диагонали АС и равен ее половине по свойству средней линии.
Аналогично, отрезок PK параллелен АС и равен ее половине. Следовательно, отрезки MN и PK равны и параллельны. По признаку MNPK – параллелограмм.
Для невыпуклого и пространственного четырехугольников доказательство аналогичное.
1. Если ABCD – выпуклый четырехугольник и M , N , P , K – середины его сторон АВ, ВС, CD и AD соответственно, то 
Д о к а з а т е л ь с т в о. Треугольники MBN и АВС подобны, следовательно, 


Аналогично, 


Имеем, 
2. Середины сторон прямоугольника являются вершинами ромба.
3. Середины сторон равнобедренной трапеции являются вершинами ромба.
4. Середины сторон ромба являются вершинами прямоугольника.
Осмыслению ключевой задачи будут способствовать вопросы: Каким условиям должны удовлетворять диагонали данного четырехугольника, чтобы середины его сторон были вершинами прямоугольника, ромба, квадрата? Докажите, что середины сторон трапеции со взаимно перпендикулярными диагоналями являются вершинами прямоугольника.
Составьте обратную задачу. Верна ли она?
Задача 1. Докажите, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Д о к а з а т е л ь с т в о. Пусть медианы АА 1 и СС 1 пересекаются в точке О . Отметим точки К и Р – середины отрезков АО и СО . Тогда точки К, Р, С 1 и А 1 середины сторон невыпуклого четырехугольника
АВСО . Следовательно, по ключевой задаче КРС 1 А 1 – параллелограмм. Его диагонали точкой пересечения делятся пополам. Тогда 
Рассуждая аналогично, докажем, что медианы АА 1 и ВВ 1 пересекаются в точке Q и 
Задача 2. Докажите, что отрезки, соединяющие середины сторон скрещивающихся ребер тетраэдра пересекаются в одной точке.
Д о к а з а т е л ь с т в о. По ключевой задаче MKPN и MLPR – параллелограммы. Их диагонали пересекаются в одной точке и делятся ею пополам.
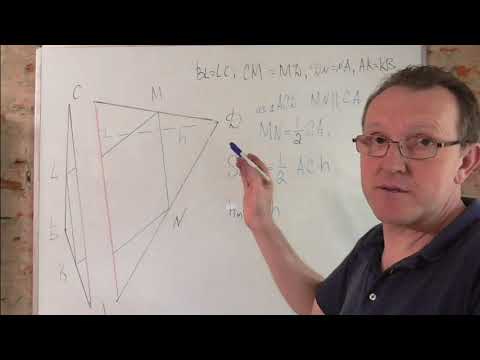
Задача 3. Диагонали трапеции взаимно перпендикулярны, длина одной из них равна 6. Длина отрезка, соединяющего середины оснований, равна 5. Найдите площадь трапеции.
Р е ш е н и е. Пусть M и P – середины боковых сторон трапеции. Тогда по ключевой задаче MNPK – прямоугольник. Так как 




Задача 4. В выпуклом четырехугольнике длины диагоналей 2 и 4. Найдите площадь четырехугольника, зная, что длины отрезков, соединяющих середины противоположных сторон равны.
Р е ш е н и е. По ключевой задаче MNPK – параллелограмм. Так как его диагонали равны, то MNPK – прямоугольник. Диагонали данного выпуклого четырехугольника параллельны сторонам прямоугольника и, следовательно, перпендикулярны. Найдем площадь выпуклого четырехугольника как половину произведения диагоналей на синус угла между ними. 
Задача 5. В выпуклом четырехугольнике ABCD длина отрезка, соединяющего середины сторон AB и CD , равна одному метру. Прямые BC и А D перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей AC и В D .
Р е ш е н и е. Обозначим через M , N , P , K – середины сторон АВ, В D , CD и АС соответственно. Тогда MK ║ NP ║ BC как средние линии треугольников BAC и BDC . Аналогично, MN ║ KP ║ AD . Так как прямые BC и А D перпендикулярны, то параллельные им прямые МК и MN также перпендикулярны. Следовательно, параллелограмм MNPK является прямоугольником и 
Задачи для самостоятельного решения
1. Найдите площадь четырехугольника, если известно, что отрезки, соединяющие середины его смежных сторон, равны 2 и 3, а угол между ними 30 0 .
2. Найдите площадь четырехугольника, если известно, что отрезки, соединяющие середины его противоположных сторон, равны 3 и 4, а длина одной из диагоналей четырехугольника равна 5.
3. Найдите площадь четырехугольника, если известно, что отрезки, соединяющие середины его смежных сторон, равны 3 и 4, а длина одного из отрезков, соединяющих середины противоположных сторон, равна 5.
4. В равнобедренной трапеции длина средней линии равна 5см, а диагонали взаимно перпендикулярны. Найдите площадь трапеции.
5. В выпуклом пятиугольнике ABCDE с единичными сторонами середины P , Q сторон AB , CD и S , T сторон BC , DE соединены отрезками PQ и ST . Пусть M и N – середины отрезков PQ и ST . Найдите длину MN .
📺 Видео
5 класс, 2 урок, Отрезок. Длина отрезка. ТреугольникСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Математика 5 класс. Отрезок. Длина отрезка. Сравнение отрезков. Единицы измеренияСкачать

ЕГЭ Математика 16 Задание Планиметрическая задача Четырехугольники Середины сторонСкачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать