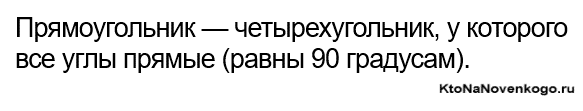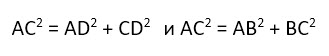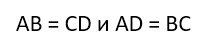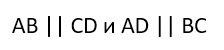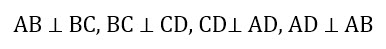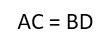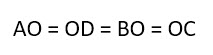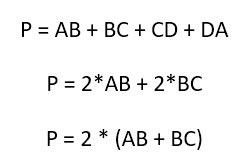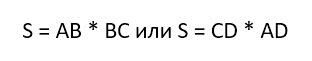Является ли четырехугольник прямоугольником если все его углы равны все его стороны равны (2 видео)

Прямоугольник — это одна из основ геометрии

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.

Название это весьма говорящее, и в нем скрыто официальное определение.

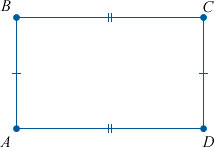
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.

Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.

Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».

Содержание

Прямоугольник — это.
Признаки прямоугольника
Диагонали прямоугольника
Свойства прямоугольника
Периметр и площадь
Комментарии и отзывы (5)
Если в четырехугольнике все углы равны
Прямоугольник
Особое свойство прямоугольника
Доказательство
Теорема
Доказательство
Теорема
Доказательство
🎦 Видео

Видео:№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать

Прямоугольник — это.

Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).

У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.

То есть выглядит это так:

Так вот, прямоугольник в данном случае является частным случаем параллелограмма.

У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.

У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.

Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.

Видео:№410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимноСкачать

Признаки прямоугольника

Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.

В случае с прямоугольником их всего три:

Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.

» alt=»»>

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

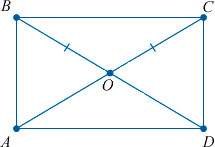
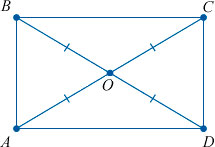
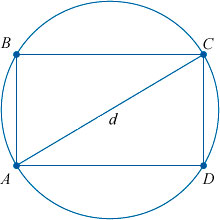
Диагонали прямоугольника

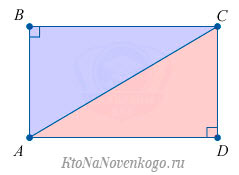
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.

Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».

В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:

Видео:Прямоугольник. 8 класс.Скачать

Свойства прямоугольника

К свойствам прямоугольника относятся следующие утверждения:

является параллелограммом

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Периметр и площадь

Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.

Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:

Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:

К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.

Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (5)

Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.

Прямоугольник отличается от квадрата, этому учат в школе в младших классах. Квадрат — это одинаковая длина соединяющих углов, если я правильно выражаюсь, а прямоугольник формы может быть: телефон, звуковые колонки, паспорт и прочее.

Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.

Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.

Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.

Видео:8 класс, 4 урок, ПараллелограммСкачать

Если в четырехугольнике все углы равны

Если в четырехугольнике все углы равны, то что можно сказать о таком четырехугольнике?

(5-й признак прямоугольника)

Если в четырехугольнике все углы равны, то этот четырехугольник является прямоугольником.

2) Если у четырехугольника три угла прямые, то этот четырехугольник — прямоугольник (по 4-му признаку).

Значит, ABCD — прямоугольник.

Что и требовалось доказать.

Если утверждение о сумме углов выпуклого четырехугольника к началу изучения темы «Прямоугольник» еще не было доказано, это можно сделать непосредственно в доказательстве 5-го признака прямоугольника.

Тогда 1-й пункт принимает такой вид:

1) Проведем в четырехугольнике ABCD диагональ AC.

Она разбивает четырехугольник на треугольники

∠BAC+∠ABC+∠BCA=180º и ∠ACD+∠CDA+∠DAC=180º.

Сумма углов четырехугольника ABCD равна сумме углов этих треугольников:

По условию, в четырехугольнике ABCD все углы равны. Поэтому ∠A=∠B=∠C=∠D=360º:4=90º.

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Прямоугольник

Частным видом параллелограмма является прямоугольник.

Прямоугольником называют параллелограмм, у которого все углы прямые

ABCD — прямоугольник.

Особое свойство прямоугольника

Диагонали прямоугольника равны

Доказательство

Дано: ABCD — прямоугольник

Доказать: AC = DB

Доказательство:

Рассмотрим ABD иACB: ABCD — прямоугольник, А и B — прямые, ABD иACB — прямоугольные. AD = CB (по свойству параллелограмма). AB — общий катет, ABD =ACB (по двум катетам). А в равных треугольниках против соответственно равных углов лежат равные стороны, значит, AC = DB, что и требовалось доказать.

Теорема

Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник

Доказательство

Дано: ABCD — параллелограмм, AC = DB

Доказать: ABCD — прямоугольник

Доказательство:

Рассмотрим ABD иACB:

AC = DB (по условию), AD = BC (по свойству параллелограмма), AB — общая, ABD =ACB (по трем сторонам). А в равных треугольниках против соответственно равных сторон лежат равные углы, A = B. А в параллелограмме противоположные углы равны, значит A = C и В = D, A = В = C = D (1). A + В + C + D = 360 0 (2)(т.к. параллелограмм выпуклый четырёхугольник). Следовательно, из (2), учитывая (1), получаем, что A = В = C = D = 90 0 , ABCD — прямоугольник, что и требовалось доказать.

Теорема

Если один из углов параллелограмма прямой, то этот параллелограмм — прямоугольник

Доказательство

Дано: ABCD — параллелограмм, A = 90 0

Доказать: ABCD — прямоугольник

Доказательство:

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0 , т.е. A + В = 180 0 , В = 180 0 — A = 180 0 — 90 0 = 90 0

Противолежащие углы параллелограмма равны, A = C = 90 0 и В = D = 90 0

Итак: ABCD — параллелограмм (по условию), и все его углы прямые (по доказанному выше), ABCD — прямоугольник (по определению), что и требовалось доказать.

Две теоремы, доказанные выше, называют признаками прямоугольника.

Поделись с друзьями в социальных сетях: