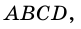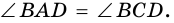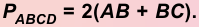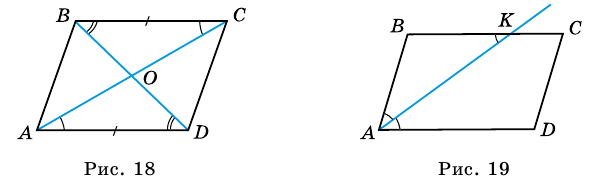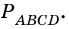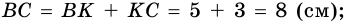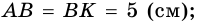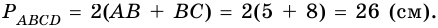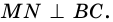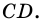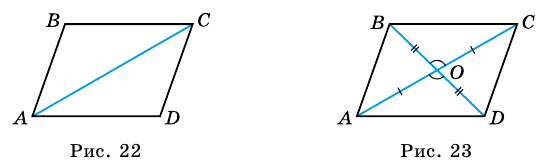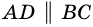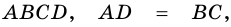Видео:Геометрия Докажите, что если сумма углов, прилежащих к любой из двух соседних сторонСкачать

Ваш ответ
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

решение вопроса
Видео:№429. Докажите, что выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащихСкачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,727
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Геометрия Если в четырехугольнике сумма противолежащих углов равна 180, то около него можно описатьСкачать

Параллелограмм, его свойства и признаки с примерами решения
Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.
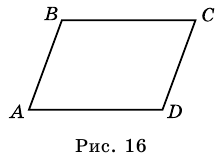
На рисунке 16 изображен параллелограмм
Рассмотрим свойства параллелограмма.
1. Сумма двух любых соседних углов параллелограмма равна 180°.
Действительно, углы 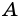
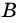
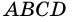
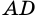
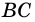
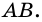
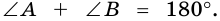
2. Параллелограмм является выпуклым четырехугольником.
Так как 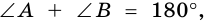
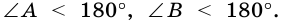
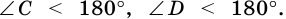
3. В параллелограмме противолежащие стороны равны и противолежащие углы равны.
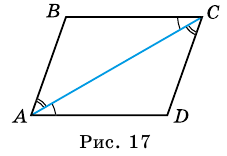
Доказательство:
Диагональ 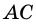
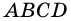
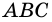
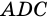
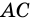
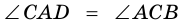
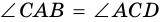
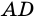
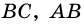
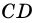
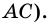
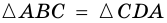
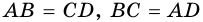
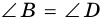
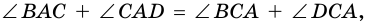
4. Периметр параллелограмма
5. Диагонали параллелограмма точкой пересечения делятся пополам.
Доказательство:
Пусть 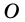
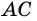
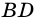
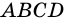
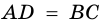
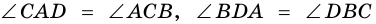
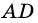
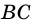
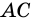
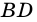
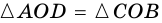
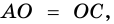
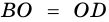
Пример:
Дано: 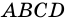
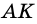
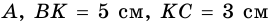
Решение:
1)
2) 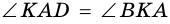
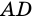
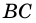
3) 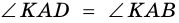
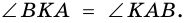
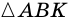
4)
Высотой параллелограмма называют перпендикуляр, проведенный из любой точки стороны параллелограмма к прямой, содержащей противолежащую сторону.
На рисунке 20 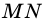
Из каждой вершины параллелограмма можно провести две высоты. Например, на рисунке 21 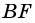
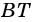
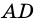
Рассмотрим признаки параллелограмма.
Теорема (признаки параллелограмма). Если в четырехугольнике: 1) две стороны параллельны и равны, или 2) противолежащие стороны попарно равны, или 3) диагонали точкой пересечения делятся пополам, или 4) противолежащие углы попарно равны, — то четырехугольник является параллелограммом.
Доказательство:
1) Пусть в четырехугольнике 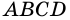
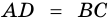

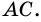
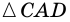
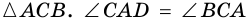
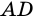
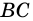
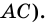
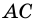
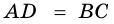
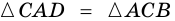
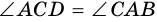
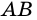
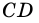
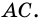
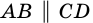
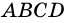
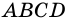
2) Пусть в четырехугольнике 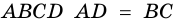
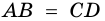
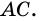
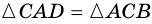
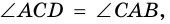
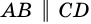
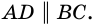
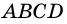
3) Пусть в четырехугольнике 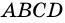
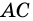
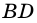
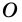
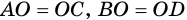
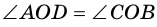
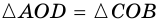
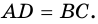
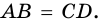
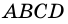
4) Пусть в параллелограмме 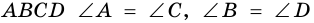
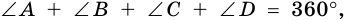
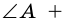
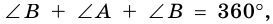
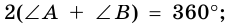
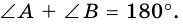
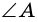
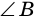
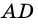
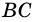
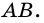
по признаку параллельности прямых). Аналогично доказываем, что 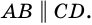
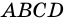
Пример:
В четырехугольнике 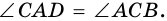
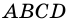
Доказательство:
Пусть 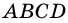

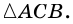
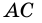
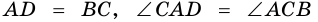
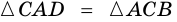
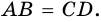
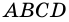
О некоторых видах четырехугольников (квадраты, прямоугольники, равнобокие и прямоугольные трапеции) знали еще древнеегипетские и вавилонские математики.
Термин «параллелограмм» греческого происхождения, считают, что он был введен Евклидом (около 300 г. до н. э.). Также известно, что еще раньше о параллелограмме и некоторых его свойствах уже знали ученики школы Пифагора («пифагорейцы»).
В «Началах» Евклида доказана следующая теорема: в параллелограмме противолежащие стороны равны и противолежащие углы равны, а диагональ делит его пополам, но не упоминается о том, что точка пересечения диагоналей параллелограмма делит каждую из них пополам.
Евклид также не упоминает ни о прямоугольнике, ни о ромбе.
Полная теория параллелограммов была разработана лишь в конце Средневековья, а в учебниках она появилась в XVII в. Все теоремы и свойства параллелограмма в этих учебниках основывались на аксиоме параллельности Евклида.
Термин «диагональ» — греческого происхождения; «диа» означает «через», а «гониос» — «угол», что можно понимать как отрезок, соединяющий вершины углов.
Следует отметить, что Евклид, как и большинство математиков того времени, для названия отрезка, соединяющего противолежащие вершины четырехугольника, в частности прямоугольника, употреблял другой термин — «диаметр». Это можно объяснить тем, что первые геометры свои рассуждения основывали на вписанных в окружность прямоугольниках. В Средние века для названия упомянутого отрезка использовали оба термина. Лишь в XVIII в. термин «диагональ» стал общепринятым.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Площадь параллелограмма
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Четырехугольники и окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:ПАРАЛЛЕЛОГРАММ и его свойства. §2 геометрия 8 классСкачать

Параллелограмм. Свойства и признаки параллелограмма
Видео:8 класс, 4 урок, ПараллелограммСкачать

Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
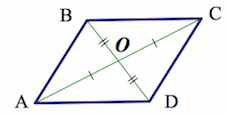
6. Точка пересечения диагоналей является центром симметрии параллелограмма
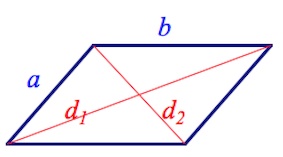
7. Диагонали параллелограмма и стороны
связаны следующим соотношением:
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны:
2. Противоположные углы попарно равны:
3. Диагонали пересекаются и в точке пересечения делятся пополам
4. Противоположные стороны равны и параллельны:
5.
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:

Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.
📸 Видео
Свойство биссектрис углов параллелограмма, прилежащих к одной сторонеСкачать
8 класс, 2 урок, Выпуклый многоугольникСкачать

Вариант 2, № 2. Сумма соседних углов параллелограмма. Пример 2Скачать

8 класс, 3 урок, ЧетырехугольникСкачать

Геометрия 8 класс. Урок 1. Четырехугольник и его элементыСкачать

Геометрия 8 класс. Параллелограмм, свойства параллелограммаСкачать

Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

ЧЕТЫРЕХУГОЛЬНИКИ и их свойства+доказательство теорем/8 класс.Скачать

Четырехугольник | Геометрия 7-9 класс #41 | ИнфоурокСкачать

Чему равна сумма углов выпуклого многоугольникаСкачать

ЧетырехугольникиСкачать