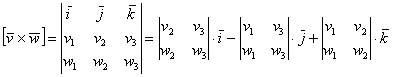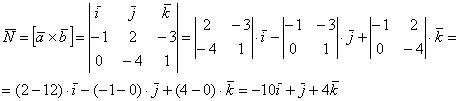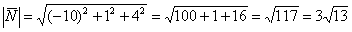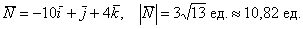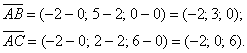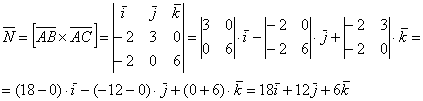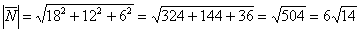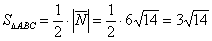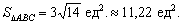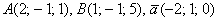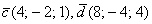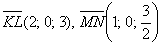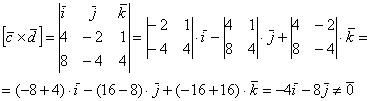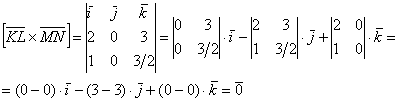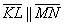В ортонормированном базисе заданы вектора (4 видео)

В ортонормированном базисе заданы вектора

В ортонормированном базисе заданы векторы а=(2; -3;1) b=(-1;2;0). Найти вектор с, перпендикулярный векторам а и b, длина которого равна единице.

Находим вектор d, перпендикулярный двум заданным с помощью векторного произведения.

-1 2 0| -1 2 = 0i – 1j + 4k – 0j – 2i – 3k = -2i – 1j + 1k.

Вектор d = (-2; -1; 1), его модуль равен √((-2)² + (-1)² + 1²) = √6.

Вектор «с» с единичной длиной получим из вектора d, разделив его на его же модуль.

Видео:Как разложить вектор по базису - bezbotvyСкачать

1.9.3. Векторное произведение в координатах

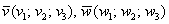
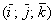
Векторное произведение векторов , заданных в ортонормированном базисе , выражается формулой:

В верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов 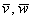, причём укладываем их в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ».

Данный определитель всегда раскрываем по первой строке, что продемонстрировано выше. Что получается в результате раскрытия определителя? В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор:

Задача 51

Найти векторное произведение векторов 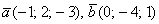и его длину.

Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), а во-вторых – его длину.

1) Найдём векторное произведение:

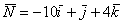
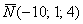
В результате получен вектор или .

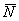
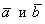
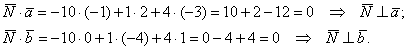
Выполним проверку: по определению, вектор должен быть ортогонален векторам . Ортогональность векторов, как мы помним, проверяется с помощью скалярного произведения:

– если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя.

2) Вычислим длину векторного произведения. Используем простейшую формулу для вычисления длины вектора:

Ответ:

Аналогичный пример для самостоятельного решения:

Задача 52

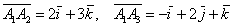
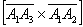
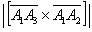
Даны векторы . Найти и вычислить .

Будьте внимательны!

Огонь камина в самом разгаре, и самое время добавить живительный геометрический смысл в наши задачи:

Задача 53

Даны вершины треугольника 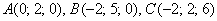. Найти его площадь.

Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:

Затем векторное произведение:

Вычислим его длину:

Формулы площадей параллелограмма и треугольника, само собой, остаются те же:

Ответ:

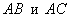
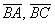
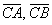
В рассмотренной задаче было не обязательно выбирать стороны , существует ещё два варианта. Решение допустимо провести через векторы либо . Желающие могут проверить, что во всех трёх случаях получится один и тот же ответ. …Почему именно эти стороны? Мысленно представьте или изобразите на черновике этот треугольник.

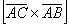
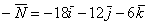
Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения. Действительно, если находить , то получим противоположно направленный вектор , но формула вычисления длины вектора всё равно «съест» эти минусы. Заметьте, что такую перестановку нельзя делать в Задачах 51-52, поскольку там требовалось найти вполне конкретный вектор.

Задача 54

Вычислить площадь параллелограмма, построенного на векторах 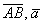, если

Самостоятельно. Решение и ответ в конце книги.

И в заключение параграфа обещанная задача:

Задача 55

Проверить, будут ли коллинеарны следующие векторы пространства:

а)

б)

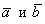
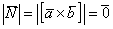
Решение: проверка основана на упомянутом ранее факте: если векторы коллинеарны, то их векторное произведение равно нулевому вектору: .

а) Найдём векторное произведение:

Таким образом, векторы 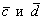не коллинеарны.

б) Найдём векторное произведение:

Значит,

Ответ: а) не коллинеарны, б)

Вот, пожалуй, и все основные сведения о векторном произведении векторов.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

35. Ортонормированные базисы в евклидовом пространстве

Определение 51. Базис Е = (Е1, Е2, . , Еn) пространства Еn называется Ортонормированным, если все его векторы единичные и попарно ортогональные.

Замечание. В примере 1 пункта 7.2 заданный базис является ортонормированным. Во втором примере этого пункта базис не ортонормированный.

Если базисные векторы единичные, но не все попарно ортогональны, то базис называется Нормированным. Если базисные векторы попарно ортогональны, но не все единичные, то базис называется Ортогональным.

Теорема 43. Любой базис евклидова пространства можно ортонормировать.

Доказательство. Пусть Е = (Е1, Е2, . , Еn) – произвольный базис пространства Еn. Доказательство проведём в два этапа. Сначала на основе данного базиса получим ортогональный базис, а затем полученный базис нормируем.

Пусть Е11 = Е1. Если Е2 ^ Е1, То возьмём Е21 = Е2. Если Е2 не ортогонален Е1. то найдём коэффициент A Так, чтобы вектор Е21 = AЕ1 + Е2 Был ортогонален вектору Е11. Так как вектор Е21 ¹ 0, то для этого необходимо и достаточно, чтобы (Е11, е21 ) = 0, т. е. (Е1, AЕ1 + Е2) = 0. Отсюда AЕ12 + (Е1, Е2) = 0. Так как Е1 ¹ 0. то Так как Е11 и Е21 ортогональны, то они линейно независимы. Вектор Е31 Будем искать в виде Е31 = A1 Е11 + A2 Е21 + Е3. Для того, чтобы Е31 был ортогонален Е11 И Е21, необходимо и достаточно, чтобы (Е11, Е31) = (Е21, Е31) = 0. Получаем систему

Так как определитель этой системы отличен от нуля (по формуле 43) то система имеет и только одно решение. Следовательно,

Вектор Е31 найдётся и только один. Так как векторы Е11, е21, е31 попарно ортогональны, то они линейно независимы. Если векторы Е11, е21, … , еn–11 уже получены, то вектор Еn1 будем искать в виде Еn1 = B1×Е11+ B2× е21 + … + Bn–1× еn–11 + Еn . Так как вектор Еn1 должен быть ортогонален ко всем предыдущим, то для нахождения коэффициентов B1, B2, … , Bn–1 получим систему уравнений (Е11, Еn1) = (Е21, Еn1) = … = (Еn–11, Еn1) = 0. Можно показать, что эта система всегда имеет решение и только одно. Итак, базис Е1 = (Е11, Е21, . , Еn1) –ортогональный. Разделив каждый полученный вектор на его длину, получим ортонормированный базис.

Теорема 44. Скалярное произведение в ортонормированном базисе имеет единичную матрицу Грама.

Доказательство Следует из того, что в ортонормированном базисе (Ек, ек) =1, (Ек, еs )= 0, если К ¹ s.

Следствие. Если вектор А В ортонормированном базисе имеет координаты (Х1, х2,…, хn), то ½А½= (47).

Теорема 45. Определитель матрицы Грама и все её главные угловые миноры строго положительны.

Доказательство. Пусть в данном (но произвольном) базисе матрица Грама имеет вид

Г = .

Пусть Е = (Е1, Е2, . , Еn) ортонормированный базис и Т – матрица перехода от данного базиса к базису Е. В базисе Е Матрица Грама – единичная. По формуле (43) Е = ТТ×Г×Т. Отсюда 1 = |Г |×|Т |2. Так как |Т |2 > 0,

Так как – евклидово подпространство пространства Еn с Тем же скалярным произведением, то главный угловой минор матрицы Г будет для него матрицей Грама. Но тогда, по доказанному, этот минор положителен.

Примеры. Могут ли быть матрицами Грама следующие матрицы.

1. А =

Матрица А Не может быть матрицей Грама, так как в матрице Грама все диагональные элементы должны быть положительными.

2. В =

Матрица В Не может быть матрицей Грама, так как матрица Грама должна быть симметрична относительно главной диагонали.

3. С =

Матрица С Не может быть матрицей Грама, так как |С | = –81 0, = 7 > 0. Следовательно, D является матрицей Грама.

Доказательство. В ортонормированном базисе скалярное произведение имеет единичную матрицу, поэтому

(А, В) = ХТ×Е×у = ХТ×у = (Х1, х2, … , хn) × = Х1у1 + Х2у2 + … + Хnуn.

Пример. В пространстве Е4 задан ортонормированный базис и векторы А1= (2, 1, 1, 2) и А2 = (–3, 2, –5, 1). Найти ортогональное дополнение к линейной оболочке L = .

Решение. Если L^, то В Î L^ Û (А1, В) = (А2, В) = 0. Пусть В = (Х1, х2, х3, х4). Так как базис ортонормированный, то (А1, В) = 2Х1 + х2 + х3 + 2Х4 , (А2, В) = –3Х1 + 2Х2 –5Х3 + х4 . Следовательно, В Î L^ Û Решая эту систему, получим, что