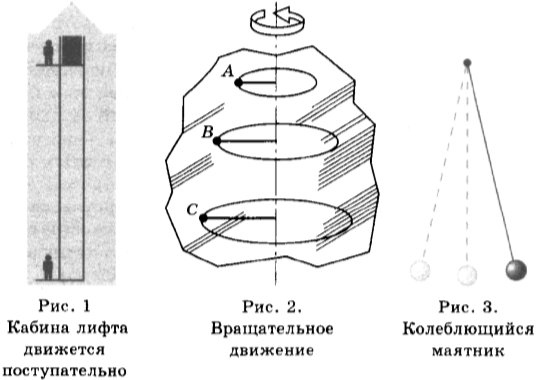
Относительно земли траектория движения колеса велосипеда окружность или (7 видео)

Механическое движение. Траектория. Путь. Перемещение

1. Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. Существуют различные виды механического движения. Если все точки тела движутся одинаково и любая прямая, проведённая в теле, при его движении остаётся параллельной самой себе, то такое движение называется поступательным (рис. 1).

Точки вращающегося колеса описывают окружности относительно оси этого колеса. Колесо как целое и все его точки совершают вращательное движение (рис. 2).

Если тело, например шарик, подвешенный на нити, отклоняется от вертикального положения то в одну, то в другую сторону, то его движение является колебательным (рис. 3).

2. В определение понятия механического движения входят слова «относительно других тел». Они означают, что данное тело может покоиться относительно одних тел и двигаться относительно других тел. Так, пассажир, сидящий в автобусе, движущемся относительно зданий, тоже движется относительно них, но покоится относительно автобуса. Плот, плывущий по течению реки, неподвижен относительно воды, но движется относительно берега (рис. 4). Таким образом, говоря о механическом движении тела, необходимо указывать тело, относительно которого данное тело движется или покоится. Такое тело называют телом отсчёта. В приведённом примере с движущимся автобусом в качестве тела отсчёта может быть выбран какой-либо дом, или дерево, или столб около автобусной остановки.

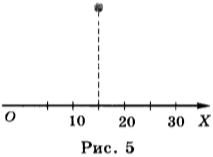
Для определения положения тела в пространстве вводят систему координат, которую связывают с телом отсчёта. При рассмотрении движения тела вдоль прямой линии используют одномерную систему координат, т.е. с телом отсчёта связывают одну координатную ось, например ось ОХ (рис. 5).

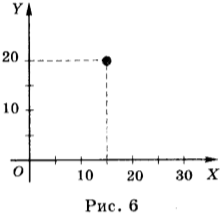
Если тело движется по криволинейной траектории, то система координат будет уже двухмерной, поскольку положение тела характеризуют две координаты X и Y (рис. 6). Таким движением является, например, движение мяча от удара футболиста или стрелы, выпущенной из лука.

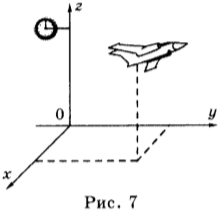
Если рассматривается движение тела в пространстве, например движение летящего самолёта, то система координат, связанная с телом отсчёта, будет состоять из трёх взаимно перпендикулярных координатных осей (OX, OY и OZ) (рис. 7).

Поскольку при движении тела его положение в пространстве, т.е. его координаты, изменяются с течением времени, то необходим прибор (часы), который позволяет измерять время и определить, какому моменту времени соответствует та или иная координата.

Таким образом, для определения положения тела в пространстве и изменения этого положения с течением времени необходимы тело отсчёта, связанная с ним система координат и способ измерения времени, т.е. часы, которые все вместе представляют собой систему отсчёта (рис. 7).

3. Изучить движение тела — это значит определить, как изменяется его положение, т.е. координата, с течением времени.

Если известно, как изменяется координата со временем, можно определить положение (координату) тела в любой момент времени.

Основная задача механики состоит в определении положения (координаты) тела в любой момент времени.

Чтобы указать, как изменяется положение тела с течением времени, нужно установить связь между величинами, характеризующими это движение, т.е. найти математическое описание движения или, иными словами, записать уравнение движения тела.

Раздел механики, изучающий способы описания движения тел, называют кинематикой.

4. Любое движущееся тело имеет определённые размеры, и его различные части занимают разные положения в пространстве. Возникает вопрос, как в таком случае определить положение тела в пространстве. В делом ряде случаев нет необходимости указывать положение каждой точки тела и для каждой точки записывать уравнение движения.

Так, поскольку при поступательном движении все точки тела движутся одинаково, то нет необходимости описывать движение каждой точки тела.

Движение каждой точки тела не нужно описывать и при решении таких задач, когда размерами тела можно пренебречь. Например, если нас интересует, с какой скоростью пловец проплывает свою дистанцию, то рассматривать движение каждой точки пловца нет необходимости. Если же необходимо определить действующую на мяч выталкивающую силу, то пренебречь размерами пловца уже нельзя. Если мы хотим вычислить время движения космического корабля от Земли до космической станции, то корабль можно считать единым целым и представить в виде некоторой точки. Если же рассчитывается режим стыковки корабля со станцией, то, представив корабль в виде точки, решить эту задачу невозможно.

Таким образом, для решения ряда задач, связанных с движением тел, вводят понятие материальной точки.

Материальной точкой называют тело, размерами которого можно пренебречь в условиях данной задачи.

В приведённых выше примерах материальной точкой можно считать пловца при расчёте скорости его движения, космический корабль при определении времени его движения.

Материальная точка — это модель реальных объектов, реальных тел. Считая тело материальной точкой, мы отвлекаемся от несущественных для решения конкретной задачи признаков, в частности, от размеров тела.

5. При перемещении тело последовательно проходит точки пространства, соединив которые, можно получить линию. Эта линия, вдоль которой движется тело, называется траекторией. Траектория может быть видимой или невидимой. Видимую траекторию описывают трамвай при движении по рельсам, лыжник, скользя по лыжне, мел, которым пишут на доске. Траектория летящего самолёта в большинстве случаев невидима, невидимой является траектория ползущего насекомого.

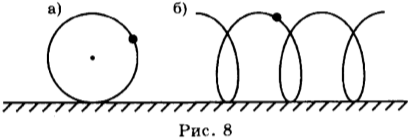
Траектория движения тела относительна: её форма зависит от выбора системы отсчёта. Так, траекторией точек обода колеса велосипеда, движущегося по прямой дороге, относительно оси колеса является окружность, а относительно Земли — винтовая линия (рис. 8 а, б).

6. Одной из характеристик механического движения является путь, пройденный телом. Путём называют физическую величину, равную расстоянию, пройденному телом вдоль траектории.

Если известны траектория тела, его начальное положение и пройденный им путь за время ( t ) , то можно найти положение тела в момент времени ( t ) . (рис. 9)

Путь обозначают буквой ( l ) (иногда ( s ) ), основная единица пути 1 м: ( [,mathrm,] ) = 1 м. Кратная единица пути — километр (1 км = 1000 м); дольные единицы — дециметр (1 дм = 0,1 м), сантиметр (1 см = 0,01 м) и миллиметр (1 мм = 0,001 м).

Путь — величина относительная, значение пути зависит от выбора системы отсчёта. Так, путь пассажира, переходящего из конца движущегося автобуса к его передней двери, равен длине автобуса в системе отсчёта, связанной с автобусом. В системе отсчёта, связанной с Землёй, он равен сумме длины автобуса и пути, который проехал автобус относительно Земли.

7. Если траектория движения тела неизвестна, то значение пути не позволит установить его положение в любой момент времени, поскольку направление движения тела не определено. В этом случае используют другую характеристику механического движения — перемещение.

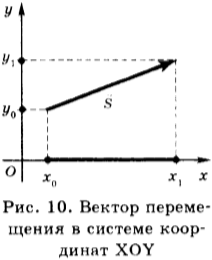
Перемещение — вектор, соединяющий начальное положение тела с его конечным положением (рис. 10)

Перемещение — векторная физическая величина, имеет направление и числовое значение, обозначается ( overrightarrow ~~) . Единица перемещения ( [,mathrm~~,] ) = 1 м.~~~~

Зная начальное положение тела, его перемещение (направление и модуль) за некоторый промежуток времени, можно определить положение тела в конце этого промежутка времени.

Следует иметь в виду, что перемещение в общем случае не совпадает с траекторией, а модуль перемещения — с пройденным путём. Это совпадение имеет место лишь при движении тела по прямолинейной траектории в одну сторону. Например, если пловец проплыл 100-метровую дистанцию в бассейне, длина дорожки которого 50 м, то его путь равен 100 м, а модуль перемещения равен нулю.

~~Перемещение, так же как и путь, величина относительная, зависит от выбора системы отсчёта.~~

При решении задач пользуются проекциями вектора перемещения. На рисунке 10 изображены система координат и вектор перемещения в этой системе координат.

Координаты начала перемещения — ( x_0, y_0 ) ; координаты конца перемещения — ( x_1, y_1 ) . Проекция вектора перемещения на ось ОХ равна: ( s_x=x_1-x_0 ) . Проекция вектора перемещения на ось OY равна: ( s_y=y_1-y_0 ) .

~~Модуль вектора перемещения равен: ( s=sqrt ~~) .~~~~

~~Содержание~~

~~ПРИМЕРЫ ЗАДАНИЙ~~
~~Часть 1~~
~~Часть 2~~
~~Изобретаем велосипед~~
Велосипед движется прямолинейно относительно горизонтальной поверхности земли. Получите экспериментально траекторию движения точки
~~Ваш ответ~~
~~решение вопроса~~
~~Похожие вопросы~~
~~📸 Видео~~

~~Видео:Движение колеса без проскальзывания, качение | Олимпиадная физика, кинематика | 9 – 11 классСкачать~~

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

~~1. В состав системы отсчёта входят~~

1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы

~~2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ~~

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

~~3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно~~

1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора

~~4. Относительно какого тела покоится автомобиль, движущийся по автостраде?~~

1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода

5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?

1) 0
2) 20 м/с
3) 40 м/с
4) -20 м/с

6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?

1) 0
2) 15 м/с
3) 30 м/с
4) -15 м/с

~~7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?~~

1) прямая
2) окружность
3) дуга
4) винтовая линия

8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь ( l ) и модуль перемещения ( s ) мяча за всё время движения?

1) ( l ) = 3,3 м, ( s ) = 3,3 м
2) ( l ) = 3,3 м, ( s ) = 0,7 м
3) ( l ) = 0,7 м, ( s ) = 0,7 м
4) ( l ) = 0,7 м, ( s ) = 3,3 м

9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?

1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй

10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса ( R ) . Чему равны при этом путь ( l ) и модуль перемещения ( s ) точки обода?

1) ( l=2R ) , ( s=2R )
2) ( l=pi R ) , ( s=2R )
3) ( l=2R ) , ( s=pi R )
4) ( l=pi R ) , ( s=pi R ) .

11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.

ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор

ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта

12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.

ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения

ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная

Часть 2

13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.

~~Видео:Мгновенный центр вращенияСкачать~~

Изобретаем велосипед

Нам предстоит познакомиться еще с одним свойством колеса. Вообще-то говоря, это свойство мы давно знаем. Только не все задумывались над его объяснением, а возможно, не связывали наблюдаемые факты именно с колесом.

А факты таковы. Когда вы катите обруч по дороге, он движется, оставаясь в вертикальном положении. Но как только движение прекращается, обруч падает на дорогу плашмя. То же самое происходит и с волчком. Пока волчок вращается, его края не касаются пола. Остановившись, волчок немедленно падает на пол.

Обычно ось волчка остается вертикальной в течение всего времени вращения. Однако самые внимательные читатели наверняка заметили, что в отдельных случаях волчок вращается, покачиваясь, а его ось при этом как бы описывает поверхность конуса.

Если вдруг случилось, что кто-нибудь из вас в детстве не играл с волчком, нужно немедленно восполнить этот пробел. Сделайте себе волчок хотя бы из спички и небольшого картонного кружка и понаблюдайте, что он вытворяет на столе.

А мы пока попробуем установить, чем же объясняется поведение волчка, обруча и вообще вращающихся тел. Для этого придется проделать еще один опыт. Идею опыта мы позаимствовали у Тома Сойера. Том вообще-то недолюбливал дохлых крыс, но считал, что, если накинуть на шею дохлой крысы веревочную петлю и раскручивать крысу вокруг головы, получаешь много удовольствия.

Не будем настаивать, чтобы в опыте использовалась обязательно дохлая крыса. Возьмите любой грузик и привяжите его к концу веревки. Нужно проследить лишь за тем, чтобы груз был привязан крепко, а веревка оказалась достаточно прочной. Иначе, оторвавшись, груз может наделать много бед, например разбить окно.

Теперь раскрутим груз. Не обязательно крутить вокруг головы. Наблюдать за поведением груза будет удобнее, если вращать его перед собой. Все мы не раз смотрели на пропеллер самолета или настольного вентилятора. Когда пропеллер раскручивается, его лопасти как бы сливаются з один круг. Мы видим плоский полупрозрачный диск. Раскрутить грузик на веревке до такой скорости нам не удается. И все же, проявив немного воображения, мы легко представим себе плоскость, в которой вращается грузик.

Представили?

Художник тоже представил себе такую плоскость и показал нам ее на рисунке.

А теперь начинаем наблюдать. Первый важный для нас вывод сделать очень просто. Груз вращается и веревка остается натянутой. Более того, вы ощущаете, что конец тянет за руку, причем в ту сторону, в которой находится груз. Этот факт хорошо известен, и вы наверняка знаете, что сила, с которой веревка тянет за руку, называется центробежной силой. Понятно и название: грузик все время пытается как бы отодвинуться, убежать от центра вращения, а веревка его не пускает.

Теперь давайте сосредоточимся. Попробуем во время вращения груза двигать рукой, держащей веревку. Можно не только двигать рукой, а попытаться самому понемногу отклоняться вправо и влево. Будьте только осторожны, чтобы вращающийся груз не ударил вас.

Проделав опыт несколько раз, вы обязательно придете к выводу, что при различных ваших движениях плоскость, в которой вращается груз, сохраняет свое положение в пространстве.

В центре купола Исаакиевского собора в Ленинграде прикреплен канат. Канат свешивается почти до полу, и на конце его закреплен груз. Все это, вместе взятое, представляет собой маятник, названный маятником Фуко. Когда маятник раскачивается, происходит то же самое, что и в нашем опыте. Ведь в обоих случаях имеется груз, привязанный к концу веревки (каната). Другой конец закреплен, и груз движется по окружности, то есть вращается. Разница лишь в том, что в нашем опыте, вращаясь, груз совершает полные обороты, а маятник в Исаакиевском соборе при каждом колебании совершает лишь часть полного оборота.

Мы можем мысленно представить себе плоскость, в которой качается маятник. Если вы пробудете в Исаакиевском соборе достаточно долго, вы увидите, что плоскость, в которой колеблется маятник, очень медленно поворачивается относительно пола. Чтобы облегчить наблюдения, на полу собора изображен круг с делениями.

Казалось бы, два факта противоречат друг другу. Плоскость, в которой вращается грузик, стремится сохранить свое положение в пространстве, а плоскость, в которой колеблется маятник, изменяет свое положение, во всяком случае, относительно пола. На самом деле никакого противоречия нет. Плоскость, в которой колеблется маятник, именно сохраняет свое положение в пространстве, а перемещается пол собора, который вращается вместе с Землей.

Впервые такой опыт был поставлен знаменитым французским физиком и механиком Леоном Фуко в 1831 году. Свой маятник он привязал к куполу Пантеона в Париже. Опыт был поставлен именно для того, чтобы наглядно показать вращение Земли.

Факты установлены. Теперь попытаемся их объяснить. Вспомним сначала основные законы механики — законы Ньютона. Мы не раз ссылались на них по ходу рассказа, но пришла пора сформулировать их более точно.

Первый закон Ньютона гласит: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

По существу, все, что было написано выше, это рассказ о первом законе Ньютона. Если тело (в нашем случае это был груз, который мы хотели переместить из пункта А в пункт Б) находится в состоянии покоя (в нашем случае неподвижно относительно поверхности Земли), то, чтобы заставить его совершать равномерное прямолинейное движение (из пункта А в пункт Б), необходимо воздействие со стороны других тел. Таким другим телом в случае с поездом будем считать локомотив.

Когда же груз движется прямолинейно и равномерно, он действительно стремится сохранить это состояние, а воздействие других тел, в нашем случае — трение, мешает такому сохранению. Мы изыскивали различные хитроумные способы свести к минимуму воздействие других тел, когда состояние равномерного прямолинейного движения было достигнуто. Правда, в пункте Б груз надо остановить или, иначе говоря, затормозить. Для этой цели мы снова вынуждены были привлекать воздействие других тел, то есть опять же трение.

Второй закон Ньютона гласит: изменение движения пропорционально приложенной силе и происходит в том направлении, в каком действует сила. Подчиняясь второму закону Ньютона, мы прицепляли к поезду локомотив, создавая тем самым силу, изменяющую состояние покоя на состояние движения. Ясно, что поезд движется именно в ту сторону, куда направлена сила тяги локомотива.

Третий закон Ньютона утверждает, что если некоторое тело Б воздействует на тело А с некоторой силой F1, то тело А в свою очередь воздействует на тело Б с силой F2, численно равной силе F1 и направленной в противоположную сторону. И это мы наблюдали неоднократно.

Если тело Б (человек) давит на тело А (телегу) с некоторой силой (для наглядности художник изобразил нам эту ситуацию), то и тело А (телега) действует на руки человека с силой той же величины, но направленной в противоположную сторону. Телега как бы отталкивает человека от себя. Согласно второму закону Ньютона, человек должен был бы начать двигаться й направлении действия силы, то есть в направлении от телеги. Чтобы не делать этого, он упирается ногами в поверхность дороги. И тут снова человек давит на дорогу в направлении от телеги, а дорога «возвращает» ему эту силу, но в противоположном направлении. В результате телегу удается сдвинуть с места.

Вернемся к нашему опыту. Грузик, привязанный к веревке, вращается, то есть движется по окружности. Всякое тело, как мы только что установили, стремится сохранить состояние равномерного и прямолинейного (именно прямолинейного!) движения. Ну, а грузик? Грузик тоже стремится. Убедиться в этом весьма просто. Достаточно в какой-то момент времени разрезать веревку. Грузик сразу станет двигаться по прямой линии. Именно об этой возможности мы и предупреждали вас, прося взять веревку покрепче и привязать грузик по-надежнее. Прямолинейно движущиеся тела легко могут попасть в окно, в голову вашего приятеля или вообще в какое-нибудь неподобающее место.

Значит, в нашем опыте двигаться прямолинейно и равномерно, то есть подчиняться первому закону Ньютона, грузику мешает веревка. Веревка тянет груз, то есть прилагает к нему силу, направленную к центру вращения. Такая сила и называется центростремительной. Под действием этой силы в полном соответствии со вторым законом Ньютона происходит изменение движения.

В данном случае, и это очень важно понять, изменение движения состоит не в изменении величины скорости: величина скорости вращения груза в течение долгого времени остается постоянной, — а в изменении направления движения (то есть направления скорости). Действительно, под действием центростремительной силы грузик все время изменяет направление своего движения: вместо того чтобы двигаться по прямой (посмотрите на рисунок!), поворачивает к центру и так, пока не совершит полный оборот.

Ну, а третий закон Ньютона? Если веревка тянет груз по направлению к центру, то груз тянет веревку с такой же точно силой, но направленной в противоположную сторону, то есть от центра. Именно эту силу, названную центробежной, и испытывает рука, держащая веревку.

Сказанное наверняка вам давно известно. Мы повторили все это, подчиняясь третьему закону Ньютона, для того чтобы начать двигаться дальше, отталкиваясь от известных вещей. А теперь будем продолжать раскручивать грузик на конце веревки и наблюдать.

Грузик вращается в вертикальной плоскости. Пусть в некоторый момент времени он находится в самом нижнем положении. Все это изображено на рисунке (см. стр. 53).

Окружность на рисунке — это линия, или, как говорят, траектория, по которой движется груз. Плоскость, в которой совершается движение, в данном случае совпадает с плоскостью книжной странички. Точка в середине окружности — это центр вращения. Линия, направленная вертикально вниз, — веревка, и к ней привязан груз. Стрелка в середине окружности показывает направление вращения.

Каково направление движения груза? Если бы не было никаких сил, иначе говоря, если бы в рассматриваемый момент времени мы оборвали или разрезали веревку, груз стал бы двигаться в направлении стрелки А на рисунке, то есть в направлении горизонтальной прямой линии, расположенной в плоскости вращения. Равномерное (то есть с постоянной скоростью) движение вдоль этой линии и есть то состояние, которое груз стремится сохранить в соответствии с первым законом Ньютона.

Мы уже установили, что под действием силы натяжения веревки груз изменяет направление своего движения. В частности, если мы посмотрим на нашу систему через некоторое время, то и сам грузик и направление его движения изменятся так, как показано на рисунке пунктиром. Теперь наглядно видно, что изменилось именно направление движения.

Теперь отдайте веревку приятелю и попросите его вращать груз в той же плоскости и с той же скоростью, а сами ложитесь на пол и посмотрите на плоскость вращения грузика снизу. То, что вы увидите, изображено на рисунке.

Окружность, по которой вращается грузик, представляется нам в виде отрезка прямой — для наглядности художник показал ее толстой линией. Направление движения грузика, когда он находится в самом нижнем положении, показано той же тонкой стрелкой А, что и в предыдущем случае.

Предположим теперь, что мы хотим повернуть плоскость, в которой вращается груз, вокруг вертикальной линии, проходящей через центр вращения. Эта линия показана на рисунке штрихпунктиром. Чтобы наглядно представить, что мы хотим сделать, перелистните страницу с предыдущим рисунком — она тоже повернется вокруг своей оси (корешка книги).

Итак, пытаемся повернуть плоскость, в которой вращается грузик. Ясно, что, если бы удалось это сделать, направление движения груза изменилось бы так, как показано пунктирной стрелкой A1. Но согласно второму закону Ньютона, изменить движение, в частном случае изменить направление этого движения, можно, лишь приложив соответствующим образом направленную силу.

Обдумав еще раз все, что мы узнали, легко приходим к следующему выводу: изменить направление движения грузика можно, лишь приложив силу, направленную так, как показано на рисунке, то есть перпендикулярно к плоскости вращения, а заодно и перпендикулярно к направлению веревки. Чтобы вы не запутались, художник изобразил силу толстой сплошной стрелкой.

Сделайте еще один опыт. Положите грузик на землю или на стол и дергайте за веревку вертикально вверх. Только строго вверх. Легко убедиться, что, поступая таким образом, можно заставить груз подниматься и опускаться, но нельзя сдвинуть его ни вправо, ни влево. Действительно, с помощью веревки невозможно создать силу, направленную перпендикулярно к тому направлению, в котором веревка натянута.

Теперь мы можем сделать несколько важных выводов. Во-первых, всякое вращающееся тело стремится сохранить неизменным положение в пространстве плоскости, в которой это тело вращается. И это не есть какой-то новый закон физики, а прямое следствие первого закона Ньютона: лежа на полу, мы сразу установили, что изменение положения в пространстве плоскости вращения сопровождается изменением направления движения груза, а следовательно, вообще изменением движения.

Во-вторых, для того чтобы изменить положение в пространстве плоскости вращения, необходимо приложить силу. Про эту силу мы знаем пока только то, что она должна быть направлена перпендикулярно плоскости вращения. Такая сила получила название кориолисовой, по имени французского математика Гюстава Гаспара Кориолиса. Кориолис прославился многими интересными работами в области математики и физики, причем одним из его наиболее значительных сочинений является математическая теория игры на бильярде.

Наш первый вывод объясняет, почему не падает вращающийся волчок и катящийся обруч. И волчок и обруч стремятся сохранить неизменным положение в пространстве плоскости своего вращения. Причем в случае волчка эта плоскость расположена параллельно земной поверхности (полу), а в случае обруча — перпендикулярно земной поверхности.

Второй вывод подсказывает нам, как поступить для того, чтобы вращающийся волчок не упал. Нужно приложить силу, направленную перпендикулярно его плоскости вращения. Можем проделать такой опыт. На вращающийся волчок бросим сверху, например, маленький бумажный шарик. Если опыт удастся (а если нет, его стоит повторить несколько раз), то волчок не упадет. Просто ось его вращения перестанет быть направленной перпендикулярно полу, а начнет покачиваться, описывая в пространстве конус. Подобное явление пока что необъяснимо на основе сделанных нами выводов.

Попробуем рассуждать дальше. До сих пор мы рассматривали вращение грузика, привязанного к веревке, лишь в тот момент, когда грузик находился в крайнем нижнем положении. Будем наблюдать дальше. Выберем момент, когда груз находится в крайнем правом положении, когда веревка, удерживающая груз, направлена параллельно земле (вправо). Этот случай также показан на рисунке а, причем направление движения груза снова помечено стрелкой А.

Теперь не надо ложиться на пол. Снова попросив подержать веревку приятеля, зайдите с правой стороны и взгляните на грузик так, чтобы плоскость его вращения слилась в одну прямую линию. И снова представьте себе мысленно, что произойдет, если повернуть плоскость вращения грузика вокруг вертикальной линии, проходящей через центр вращения.

Картина, представшая нашему мысленному взору, весьма интересна (на всякий случай посмотрите, как художник представил ее на бумаге). Оказывается, при таком положении грузика поворот плоскости вращения не сопровождается ни изменением направления движения, ни изменением скорости этого движения. Направление движения грузика как бы переносится в пространстве параллельно самому себе. А раз движение не изменяется ни по скорости, ни по направлению, то, согласно второму закону Ньютона, нет необходимости в какой-то дополнительной силе.

Обнаружение столь интересного факта, естественно, побуждает нас продолжить наблюдения. Остановимся теперь на моменте, когда грузик находится в крайнем верхнем положении. Направление движения грузика изображено горизонтальной стрелкой, направленной влево.

Снова передаем приятелю веревку и взлетаем над объектом наблюдения. Тем, кому не удастся взлететь, можем посоветовать залезть на стул. Снова, в третий раз, представляем себе мысленно поворот плоскости вращения вокруг вертикальной линии, проходящей через центр вращения. Нужно договориться еще о том, в какую сторону вращать грузик. Точнее, нужно представить себе, что мы поворачиваем плоскость вращения в ту же сторону, что и при первом наблюдении (смотри рисунок б).

Поглядев теперь на рисунок, соответствующий первому наблюдению, мы увидим, что для наблюдателя, расположенного сверху, плоскость вращения поворачивалась по часовой стрелке. Мысленно повернув ее в ту же сторону, видим, что направление движения грузика снова меняется, а значит, снова возникает необходимость в приложении кориолисовой силы. Эта сила, как и прежде, перпендикулярна плоскости вращения, однако направлена в противоположную сторону. Если при самом первом наблюдении кориолисова сила была направлена к наблюдателю, рассматривающему страницу с рисунком, то теперь она направлена от наблюдателя.

Сделаем, наконец, четвертое наблюдение. Выберем момент, когда веревка, удерживающая грузик, направлена горизонтально и влево. Нашему подготовленному взору сразу бросается в глаза, что направление движения грузика не изменяется — оно лишь перемещается параллельно самому себе. Кориолисова сила снова отсутствует.

Теперь от нас требуется последнее усилие. Представим себе не грузик, привязанный к веревке, а колесо со спицами — обыкновенное велосипедное колесо. Пусть колесо вращается в вертикальной плоскости. Мысленно разделим колесо на небольшие части, например так, чтобы каждая часть примыкала к одной из спиц. Тогда каждую часть колеса мы можем уподобить грузику, привязанному к веревке.

Не надо специально выбирать моменты наблюдения, поскольку в любой момент у нас имеются части, расположенные и сверху, и снизу, и справа, и слева. Пока плоскость, в которой вращается колесо, сохраняет свое положение в пространстве, ничего особенного не происходит. Но если мы попытаемся повернуть плоскость вращения колеса опять-таки относительно вертикальной линии, проходящей через центр вращения (направление поворота плоскости вращения и здесь помечено стрелкой А), произойдет следующее.

Части колеса, расположенные справа и слева, не испытывают действия никаких сил. Части же колеса, расположенные сверху и снизу, испытывают действие сил, направленных так, как показано на рисунке черными стрелками, помеченными буквами F. Очевидно, что эти силы стремятся повернуть плоскость вращения колеса относительно горизонтальной линии, проходящей через центр.

Проделав еще один цикл наблюдений, аналогичный уже описанному, мы легко убедимся, что справедливо и обратное. Всякая попытка повернуть плоскость вращения относительно горизонтальной линии, проходящей через центр, приведет к появлению пары сил (сил Кориолиса), стремящихся повернуть ту же плоскость относительно вертикальной оси.

О том, что все сказанное справедливо, знает всякий, кому хоть раз приходилось ехать на велосипеде. Если вы разогнали велосипед по прямой, то при наличии достаточного опыта можете бросить руль и даже встать на седло или сесть на него задом наперед. Велосипед будет продолжать двигаться строго по прямой и сохранять вертикальное положение. Происходит это потому, что оба колеса стремятся сохранить положение плоскости своего вращения в пространстве. Если вам надо повернуть, например, вправо, тоже необязательно браться за руль. Достаточно движением корпуса слегка отклонить велосипед вправо. Возникающие при этом силы Кориолиса повернут переднее колесо, а точнее, плоскость, в которой оно вращается, в нужном направлении.

А вот начинающему велосипедисту особенно важно знать следующее. Если вы едете на велосипеде и по какой-то причине он начал валиться набок, например влево, нужно срочно повернуть руль в ту же сторону. Если скорость вращения достаточна, возникающие при этом силы Кориолиса удержат вас от падения и помогут восстановить вертикальное положение велосипеда.

Узнав все это, мы легко ответим на вопрос: почему не падает набок описанный выше одноколесный экипаж? А вот если мы заменим в этом экипаже колесо гусеницей, подобной гусенице танка, ничего хорошего не получится. У танка и трактора предпочтительно иметь две гусеницы, расположенные по обеим сторонам корпуса. Дать полное объяснение этому факту мы предоставляем читателю. Намекнем только, что большая часть звеньев гусеницы не вращается, а движется по прямолинейным траекториям.

Многое еще можно было бы рассказать о колесе, но пора и честь знать. Заметим в заключение, что хотя само колесо было изобретено около шести тысяч лет назад, некоторые основные его свойства, такие, скажем, как наличие кориолисовых сил, были открыты лишь в середине прошлого века. Колесо в его современном виде — с резиновой шиной и шарикоподшипниками — появилось еще позже. А некоторые подробности, связанные с силами трения, досконально не изучены специалистами и по сей день. Впереди еще много несделанных открытий, связанных с колесом. Поэтому не надо стесняться — смело изобретайте велосипед.

~~Видео:Физика - движение по окружностиСкачать~~