Калькулятор по треугольнику паскаля (6 видео)

Треугольник Паскаля

Треугольником Паскаля называется бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.

№	Треугольник Паскаля
0	1
1	1 1
2	1 2 1
3	1 3 3 1
4	1 4 6 4 1
5	1 5 10 10 5 1
6	1 6 15 20 15 6 1
…	…

Треугольник Паскаля можно получить из таблицы натуральных степеней бинома x + y

Содержание

Натуральные степени бинома x + y
Свойства треугольника Паскаля
Определения
Написать разложение вида: (x + y) 7
Треугольник Паскаля
All-Calc.com
Архивы
Треугольник Паскаля
📽️ Видео

Натуральные степени бинома x + y

№	Степень	Разложение в сумму одночленов
0	(x + y) 0 =	1
1	(x + y) 1 =	1x + 1y
2	(x + y) 2 =	1x 2 + 2xy + 1y 2
3	(x + y) 3 =	1x 3 + 3x 2 y + 3xy 2 + 1y 3
4	(x + y) 4 =	1x 4 + 4x 3 y + 6x 2 y 2 + 4xy 3 + 1y 4
5	(x + y) 5 =	1x 5 + 5x 4 y + 10x 3 y 2 + 10x 2 y 3 + 5xy 4 + 1y 5
6	(x + y) 6 =	1x 6 + 6x 5 y + 15x 4 y 2 + 20x 3 y 3 + 15x 2 y 4 + 6xy 5 + 1y 6
…	…	…

Свойства треугольника Паскаля

Сумма чисел n-ной строки (отсчет ведется с нуля) треугольника Паскаля равна 2 n . Действительно, при переходе от каждой строки к следующей сумма членов удваивается, а для нулевой строки она равна 2 0 =1 .
Все строки треугольника Паскаля симметричны. Потому что при переходе от каждой строки к следующей свойство симметричности сохраняется, а нулевая строка симметрична.
Каждое число в треугольнике Паскаля равно C_n k , где n — номер строки, k — номер (отсчет ведется с нуля) элемента в строке.
Каждое число треугольника Паскаля, уменьшенное на единицу, равно сумме всех чисел, заполняющих параллелограмм, ограниченный диагоналями, на пересечении которых находится этот элемент.
Вдоль диагоналей, параллельных сторонам треугольника, выстроены треугольные числа, тетраэдрические числа и т.д.
Если посчитать для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел, то получится соответствующее число Фибоначчи.

Определения

Треугольными числами называется количество шаров, которые можно выложить в виде равностороннего треугольника.

Тетраэдрическими числами называется количество шаров, которые можно выложить в виде правильного тетраэдра.

Последовательность f₁ = f₂ = 1 , f_n = f_n−1 + f_n−2 при n>2 называется последовательностью Фибоначчи, а ее члены — числами Фибоначчи.

Написать разложение вида: (x + y) 7

Воспользовавшись строкой треугольника Паскаля с номером 6 и применив основное свойство треугольника Паскаля, получим строку с номером 7:

Видео:Треугольник ПаскаляСкачать

Треугольник Паскаля

Если говорить о треугольнике Паскаля, то его можно охарактеризовать как бесконечную таблицу. В данной таблице используются биномиальные коэффициенты. А сама таблица представлена в виде треугольника. Чтобы произвести расчет, можно использовать калькулятор, где указывается только количество строк. При самостоятельном расчете потребуется время и знание формул.

Как уже говорилось, данный треугольник представляет собой таблицу, начинается которая с нулевой строки. Вершина таблицы и боковые стороны каждой строки имеют единицы. Остальные числа (в середине) равны сумме 2-ух чисел, которые находятся в предыдущей строке (над ними).

В данном случае используются натуральные степени бинома: х+у
Для нулевой строки: (x + y)° =
Для первой: (x + y)¹ =
Для второй: (x + y)² =
И так далее.
Если разложить в сумму одночленов, получим для нулевой: 1
Для первой: 1x + 1y
Для второй: 1x² + 2xy + 1y²
Треугольника Паскаля, для расчетов используется формула:

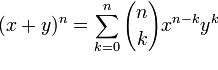
где

Видео:Числа сочетаний. Треугольник Паскаля | Ботай со мной #059 | Борис Трушин |Скачать

All-Calc.com

Архивы

Видео:Как треугольник Паскаля поможет умножать без калькулятораСкачать

Треугольник Паскаля

Данный калькулятор строит треугольник Паскаля заданного размера.

Треугольник Паскаля представляет собой таблицу чисел в виде треугольника. Числа, находящиеся в таблице являются биномиальными коэффициентами, т.е. коэффициентами перед слагаемыми при раскрытии выражения вида (a+b)^n.

Строки треугольника отсчитываются начиная с нулевой (нулевая, первая, вторая и т.д.) с вершины. Чтобы найти коэффициенты при раскрытии выражения (a+b)^n необходимо воспользоваться n-ой строкой. При этом i-ый коэффициент в строке будет стоять перед слагаемым вида a^(n-i)*b^(i), элементы в строке отсчитываются с нулевого.

Рассмотрим это на примере раскрытия квадрата суммы. Известная формула (a+b)^2 = a^2 + 2*a*b + b^2. Теперь посмотрим на коэффициенты второй строки в треугольнике Паскаля: 1 2 1. Попробуем раскрыть выражение при помощи треугольника Паскаля:

(a+b)^2 = 1*a^(2-0) + 2 * a^(2-1) * b^1 + 1 * b^2 = a^2 + 2*a*b + b^2. Формулы совпали.

Чтобы воспользоваться калькулятором, введите количество строк (n) в треугольнике, который хотите получить (обычно в качестве n используется степень раскрываемого выражения). Калькулятор построит треугольник нужного размера и по полученным коэффициентам можно будет раскрыть скобки.