Центральная симметрия четырехугольника относительно точки

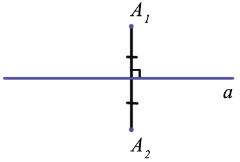
Если прямая проходит через середину отрезка А₁А₂ и перпендикулярна к нему, то точки А₁ и А₂ называются симметричными относительно прямой . Каждая точка прямой симметрична самой себе.

Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. Прямая — ось симметрии фигуры.

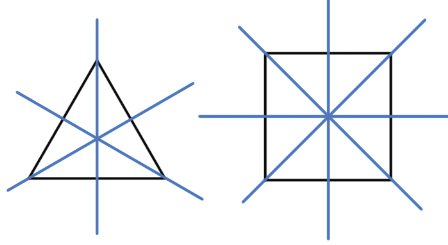
Пример (синим цветом обозначены оси симметрии):

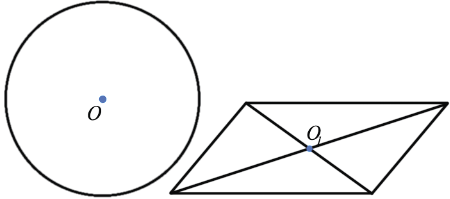
Точки А₁ и А₂ называются симметричными относительно точки О, если О — середина отрезка А₁А₂. Точка О считается симметричной самой себе.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.

Пример (синим цветом обозначены центры симметрии):

Поделись с друзьями в социальных сетях:

Видео:Центральная симметрия. 6 класс.Скачать

Осевая и центральная симметрия

О чем эта статья:

Видео:Симметрия относительно точки (центральная симметрия). Пример 2Скачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Осевая симметрия. 6 класс.Скачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Центральная симметрия. Как построить фигуру, симметричную данной относительно точкиСкачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:Центральная симметрияСкачать

Урок по теме «Построение треугольника, четырехугольника, симметричных относительно оси, центра симметрии»

Видео:Осевая и центральная симметрия, 6 классСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Видео:Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

Урок математики в 8-м специальном (коррекционном) классе VIII вида на тему:

Видео:Построение симметричного четырехугольника. #ShortsСкачать

«Построение треугольника, четырехугольника, симметричных относительно оси, центра симметрии»

Видео:Центральная и осевая симметрии. Геометрия 7 класс.Скачать

Урок математики в 8-м специальном (коррекционном) классе VIII вида на тему: «Построение треугольника, четырехугольника, симметричных относительно оси, центра симметрии»

Цели урока: актуализировать личностный смысл учащихся к изучению темы; помочь учащимся осознать социальную, практическую и личную значимость учебного материала; создать содержательные и организационные условия для развития умений строить симметричные фигуры, находить оси симметрии в различных геометрических фигурах; создать условия для творческой самореализации личности.

Образовательные: продолжить изучение понятия осевой и центральной симметрии, показать явления симметрии в природе, архитектуре и технике, уметь находить симметричные объекты в окружающем мире, приобретение навыков самостоятельной работы.

Развивающие: развитие логического мышления, творческой активности, познавательного интереса. Развивать умение кратко излагать свои мысли.

.Воспитательные: воспитание умения сплоченно и дружно работать в коллективе, внимательно слушать речь других.

Ожидаемые результаты урока:

углубить и расширить знания по теме «Симметрия»;

узнать о видах симметрии и уметь отличать один вид от другого;

получить наглядное представление о проявлении симметрии в природе, различных областях науки и человеческой деятельности;

строить треугольник, четырехугольник, симметричные относительно оси, центра симметрии.

Описание необходимых ресурсов для урока:

На уроке используются следующие ресурсы: специально разработанная POWER POINT-презентация, которая включает основные моменты хода урока, электронные ресурсы, компьютер, раздаточные материалы, рисунки, рефераты, гербарии растений, обладающих свойствами симметрии, изображения архитектурных ансамблей.

Образовательные технологии -личностно — ориентированный подход.

Для осуществления поставленных на урок задач выбраны следующие методы и формы обучения: методы — наглядный, словесный, частично-поисковый, дискуссия.

Формы — общеклассная, индивидуальная.

На доске написана тема урока «Построение треугольника, четырехугольника, симметричных относительно оси, центра симметрии»

Кабинет украшается высказываниями великих людей о симметрии и об ее роли в нашей жизни:

«Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство» (Вейль Г.)

«Математика выявляет порядок, симметрию и определенность, а это — важнейшие виды прекрасного» (Аристотель)

«Математик любит прежде всего симметрию» (Максвелл Д.)

«Красота тесно связана с симметрией» (Вейль Г.)

«Для человеческого разума симметрия обладает, по — видимому, совершенно особой притягательной силой» (Фейнман Р.)

Оформлена выставка рисунков, гербариев, выставка предметов, обладающих тем или иным видом симметрии.

1. Организационный момент: Учитель проверяет готовность класса к уроку.

2. Актуализация опорных знаний.

Учитель : Рассмотрите рисунки на доске и ответьте на вопросы:

1) Как расположены относительно друг друга пары прямых линий на рисунке? (Пересекаются или не пересекаются)

2) Назовите пары прямых линий, которые не пересекаются. Как их ещё можно назвать?

взаимно перпендикулярные линии. Как их ещё можно назвать? (Параллельные)

3) Назовите параллельные линии, которые пересекаются. Какие из них можно выделить? Как их ещё можно назвать? ( Перпендикулярные )

Назовите геометрические фигуры, расположенные на доске.( Прямая линия, отрезок, луч, треугольник, шестиугольник, квадрат прямоугольник, трапеция)

1) Чем отличается фигура 1 от фигур 2 и 3?

2) Как можно назвать фигуры 6,7,8?

3) Как можно назвать вместе фигуры 4,5,6,7,8

Учитель: На предыдущих уроках мы с вами познакомились с понятием «симметрия». Сегодня мы с вами продолжим эту тему. Откройте тетради. Запишите число и тему урока (Слайд 1) Учитель сообщает тему урока, ее цель,

Какие виды симметрии вызнаете? ( Осевая и центральная ). (Слайд 2)

Что является осью в осевой симметрии? ( прямая )

Что является центром в центральной симметрии? ( точка )

Учитель : Мы научились строить точки, симметричные относительно оси, центра симметрии. Вспомним как это делается. Учитель демонстрирует лист бумаги, о котором говорится в слайдах. (Слайды 3,4)

1) Взяли лист белой бумаги, согнули его пополам и провели прямую а по линии сгиба.

2) Проткнули двойной лист иголкой, а затем развернули лист.

3) Мы получили на нем две точки. Обозначили одну буквой А, а другую — В

4) Соединили А и В отрезком.

5) Измерили расстояние от А и от В до линии сгиба. Сделали вывод, что эти расстояния равны. Определили, что линия сгиба, которую мы обозначили как прямую а перпендикулярна отрезку АВ_. (Развиваются умения анализировать, сравнивать, выделять главное в познавательном объекте).

Две точки А и В называются симметричными относительно прямой, если эта прямая проходит через середину отрезка АВ и перпендикулярна к нему.

Учитель : Какие необходимые условия должны выполняться при построении точек, симметричных относительно оси симметрии?

Учитель : Какие необходимые условия должны выполняться при построении точек, симметричных относительно центра симметрии?

Точки A и A 1 называются симметричными относительно точки О, если О – середина отрезка AA 1.(Слайд 5)

Учитель : Вспомним правило построения отрезка, симметричного данному.( Нужно построить точки, симметричные концам отрезка относительно этой оси , а затем соединить их.

Учитель : По этому же принципу выведите правило построения треугольника, четырехугольника, симметричного данному. ( Чтобы построить треугольник, четырехугольник, симметричный данному, нужно построить точки, симметричные вершинам данного треугольника, четырехугольника, а затем соединить их.)

Учитель : Значит, чтобы построить отрезок, симметричный относительно оси, нужно построить точки симметричные концам отрезка относительно этой оси и соединить эти точки. Мы получили отрезок, симметричный данному, относительно оси.

3. Изучение нового материала

Учитель : Если дана ось симметрии и четырехугольник, сколько требуется построить точек, чтобы получить симметричный четырехугольник?

Учитель с помощью компьютера (работает диск Виртуальная математика для основной школы 5-9 классы, учитель помогает детям на местах) показывает как строится четырехугольник, симметричный данному относительно оси , центра симметрии. Учащиеся повторяют в тетрадях. (Один из учащихся выполняет построение на доске. Актуализируется субъектный опыт учащихся, осуществляется коррекция знаний). Учащиеся применяют свои знания и умения для построения).

Учитель : Что происходит с фигурой при центральной симметрии? ( При повороте вокруг точки «О» – центра симметрии на 180 0 фигура переходит сама в себя).

4. Минута релаксации – 1-2 мин.

5. Самостоятельная работа.

Учитель : А теперь каждый из вас попытается самостоятельно построить треугольник относительно оси, центра симметрии. (Раздаются чистые листы бумаги, дети чертят каждый свою фигуру, учитель проходит и каждому чертит ось или обозначает центр симметрии.) (Осуществляется самоконтроль учебной деятельности).

6. Просмотр слайдов по теме «Оси симметрии в различных геометрических фигурах, их количество», их обсуждение и подведение итогов и выводов.

Симметричность фигуры относительно прямой. (Слайд 6)

— Сколько осей симметрии имеет эта фигура? (Учащиеся обсуждают и делают соответствующие выводы).

Учитель : Ребята, укажите ось симметрии следующих геометрических фигур. (Слайд 7) (Происходит самостоятельный поиск ответов на вопросы, т.е. отыскание осей симметрии у геометрических фигур и доказательства этого, опираясь на имеющийся опыт). Все рассмотренные фигуры имеют один и тот же вид симметрии, который называется осевая симметрия.

Данную симметрию можно назвать зеркальной.

Учитель : Посмотрите на все эти рисунки. Их объединяет то, что они симметричны. Если поставить зеркальце вдоль прямой, то отраженная в зеркале половина дополнит фигуру до целой. Прямая, вдоль которой поставлено зеркало, называется осью симметрии. (Слайд 8,9,10)

— Существуют ли фигуры, не обладающие осью симметрии ? (Слайд 11)

7. Просмотр слайдов по теме «Явления симметрии в природе, архитектуре и технике», их обсуждение и подведение итогов и выводов.

Учитель : Для чего же нужна симметрия?

Учитель : По наблюдениям, в любом растении можно найти какую-то его часть, обладающую осевой или центральной симметрией. Это могут быть листья, цветы, стебли, стволы деревьев, плоды, и более мелкие части, такие как сердцевина цветка, пестик, тычинки и другие.

Центральная симметрия наиболее характерна для плодов растений и некоторых цветов. (Слайды 12,13) (Учащиеся получают интересную информацию).

Многие предметы окружающего мира имеют ось симметрии или центр симметрии. (Слайды 14-17) растения и животные (для того, чтобы вести здоровый образ жизни). (Учащиеся получают интересную информацию).

Учитель : Симметричные предметы обладают большей устойчивостью. Симметрия воспринимается человеком как проявление закономерности, а значит внутреннего порядка. Внешне этот внутренний порядок воспринимается как красота. Все это привело человека к мысли, о том, что чтобы сооружение было красивым оно должно быть симметричным.

Издавна человек использует симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.

Так, фасады многих зданий, сооружения, парки обладают осевой симметрией. (Слайды 18-23)

. Учитель : Кроме эстетической ценности симметрии, мы видим и практическую сторону этого свойства, а именно симметричность это важнейшее свойство, которыми должны обладать здания (для того, чтобы быть устойчивыми).

Симметрия в искусстве (Слайды 28-33) (Учащиеся получают интересную информацию).

Оформление зданий обладает осевой симметрией (Слайды 34,35) (Учащиеся получают интересную информацию).

Вид спереди различных видов транспорта обладает осевой симметрией. (для того, чтобы обладать максимальными параметрами качества), (Слайд 36)

Симметрия в поэзии. (Слайд 37) (Учащиеся получают интересную информацию).

Весь материал, подготовленный к этому уроку, должен расширить ваш кругозор, культуру и помочь сформировать собственный взгляд на жизнь.

8. Заключительное слово учителя. Рефлексия. Выставление оценок:

Учитель : Итак, наш урок подошел к концу.

Что нового вы сегодня узнали, чем мы занимались, чему научились? Мы научились строить симметричные фигуры, убедились в том, что симметрия присутствует и в прошлом и в будущем. Симметрия — это не только математическое понятие. (Активизация мыслительной деятельности, каждый может высказать свое мнение, высказываются разные мнения).

Учитель : Ребята! Поднимитесь те, кто сегодня на уроке хотя бы один раз дал правильный ответ. Спасибо, присаживайтесь. (Учащиеся осознают ценность совместной деятельности, повышается мотивация учебной деятельности).

Учитель : Итак, подведем итог: симметрия важна всем. Она широко распространена в быту, в природе, ее можно наблюдать в форме листьев и цветов растений, строении животных, человека, насекомых.
Симметрия широко используется на практике: в строительстве, архитектуре, технике, её мы видим и в искусстве.

9. Домашнее задание

Стр.56 № № 162 (1). Симметрию можно обнаружить почти везде, если знать, как ее искать. Привести примеры симметричных фасадов зданий нашего города и асимметричных тел.

Учитель : Закончить урок хочется словами немецкого математика Германа Вейля, который сформулировал определение симметрии сравнительно недавно — в начале ХХ века, «Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».

Если остается время. Симметрия букв. (Слайд 38) (Учащиеся обсуждают и делают соответствующие выводы). (Учащиеся получают интересную информацию и продолжают осознавать практическую значимость учебного материала).

🎦 Видео

Симметрия относительно точки. 6 классСкачать

ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

Симметрия относительно точки (центральная симметрии). Пример 1Скачать

Симметрия относительно прямой (осевая симметрия). Пример 2Скачать

ВПР 6 класс. Фигура симметричная данной относительно точки О.Скачать

Ось симметрииСкачать

Симметрия относительно точкиСкачать

Осевая и центральная симметрия.Скачать

Геометрия 8 Осевая и центральная симметрияСкачать

Осевая симметрия, как начертить треугольники симметричноСкачать