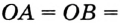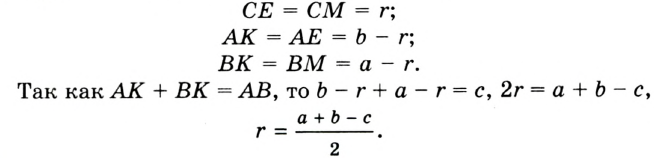Содержание:
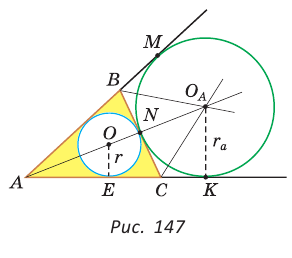
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника. На рисунке 146 изображен треугольник АВС и три его вневписанные окружности с центрами
Вневписанные окружности обладают рядом интересных свойств:
1. Центры вписанной и вневписанной окружностей лежат на биссектрисе соответствующего внутреннего угла треугольника.
2. 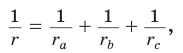
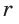
3. 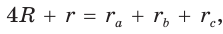
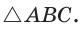
Попробуйте доказать некоторые из этих свойств.
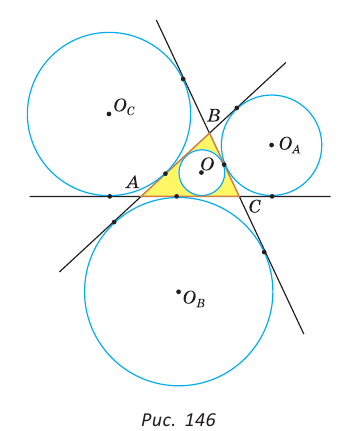
Найдем радиус 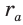
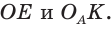
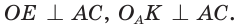
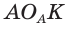
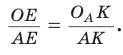
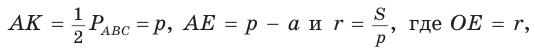
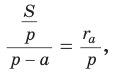
Пример:
Вычислим, используя данную формулу, радиус вневписанной окружности прямоугольного треугольника с катетами 3 и 4, которая касается гипотенузы:
- Описанная и вписанная окружности треугольника
- Прямоугольный треугольник и его описанная и вписанная окружности
- Вписанные и описанные четырехугольники
- Окружность, вписанная в треугольник
- Описанная трапеция
- Дополнительные свойства и признаки вписанного четырехугольника
- Обобщенная теорема Пифагора
- Формула Эйлера для окружностей
- Справочная информация по описанной и вписанной окружности треугольника
- Геометрия
- Понятие правильного многоугольника
- Описанная и вписанная окружности правильного многоугольника
- Формулы для правильного многоугольника
- Построение правильных многоугольников
- Формулы вписанной и описанной окружности для треугольника и квадрата
- 🔍 Видео
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Описанная и вписанная окружности треугольника
Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.
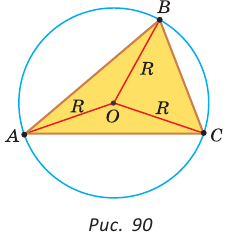
На рисунке 90 изображена окружность с радиусом R и центром 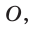
Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника.
Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС».
Теорема (об окружности, описанной около треугольника).
Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.
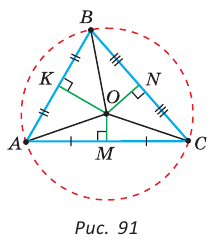
Рассмотрим произвольный треугольник АВС (рис. 91). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно.
Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них.
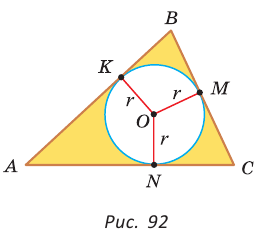
Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.
На рисунке 92 изображена окружность с центром О и радиусом 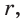
Так как 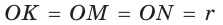
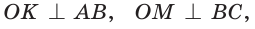
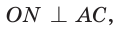
Вместо слов «окружность, вписанная в треугольник АВС», также говорят «вписанная окружность треугольника АВС».
Теорема (об окружности, вписанной в треугольник).
В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.
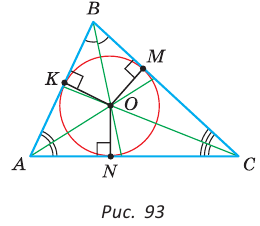
Рассмотрим произвольный треугольник АВС (рис. 93). Пусть О — точка пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОМ и ON соответственно к сторонам АВ, ВС и АС. По свойству биссектрисы угла ОК = ON, ON = ОМ. Окружность с центром в точке О и радиусом ОК будет проходить через точки К, М и N и касаться сторон АВ, ВС и АС в указанных точках по признаку касательной.
Следовательно, эта окружность является вписанной в треугольник АВС. Единственность вписанной окружности докажите самостоятельно.
Замечание. Так как все три биссектрисы треугольника пересекаются в одной точке, то для нахождения центра вписанной окружности достаточно построить точку пересечения любых двух из них.
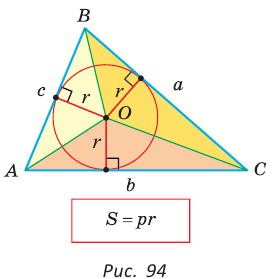
Теорема. Площадь треугольника можно найти по формуле 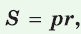
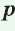
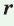
Пусть дан треугольник АВС со сторонами 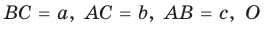
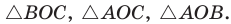
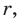
Следствие:
Радиус окружности, вписанной в треугольник, можно найти по формуле
Одной из важнейших задач данной темы является задача нахождения радиуса описанной и радиуса вписанной окружностей данного треугольника.
Пример:
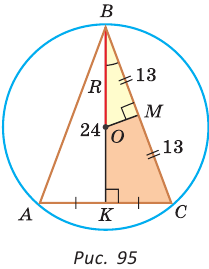
Найти радиус окружности, описанной около равнобедренного треугольника АВС, у которого АВ = ВС = 26 см, высота ВК = 24 см
(рис. 95).
Решение:
Способ 1 (метод подобия). Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Проведем серединные перпендикуляры к сторонам АС и ВС, которые пересекутся в точке О — центре описанной окружности. Так как в равнобедренном треугольнике высота, проведенная к основанию, является медианой, то ВК — серединный перпендикуляр к стороне АС. Пусть МО — серединный перпендикуляр к стороне ВС. Тогда ВМ = 13 см, ВО = R -— искомый радиус. Поскольку 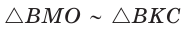
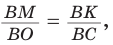
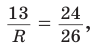
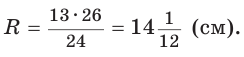
Способ 2 (тригонометрический метод). Из 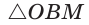
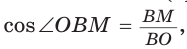
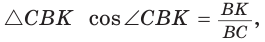
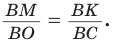
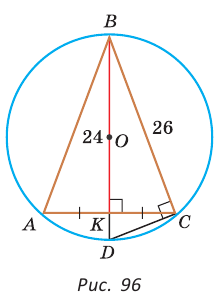
Способ 3* (среднее пропорциональное). Продлим высоту ВК до пересечения с описанной окружностью в точке D (рис. 96). Так как центр описанной окружности равнобедренного треугольника лежит на прямой ВК (см. способ 1), то BD = 2R — диаметр данной окружности. В прямоугольном треугольнике BCD 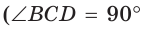
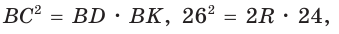
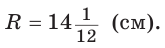
Ответ: 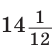
Замечание. Из решения ключевой задачи 1 следует свойство: «Центр окружности, описанной около равнобедренного треугольника, лежит на его высоте, проведенной к основанию, или на ее продолжении».
Верно и обратное утверждение: «Если центр окружности, описанной около треугольника, лежит на высоте треугольника или на ее продолжении, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Полезно запомнить!
Если в ключевой задаче 1 боковую сторону обозначить 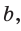
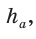
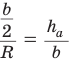
Отсюда следует удобная формула для нахождения радиуса окружности, описанной около равнобедренного треугольника:
Пример:
Найти радиус окружности, вписанной в равнобедренный треугольник АВС, у которого АВ = ВС = 10 см, АС = 12 см.
Решение:
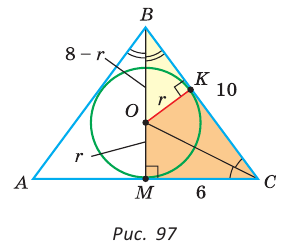
Способ 1 (метод подобия). Центр вписанной окружности находится в точке пересечения биссектрис треугольника. Проведем в треугольнике АВС биссектрисы из вершин В и С, которые пересекутся в точке О — центре вписанной окружности (рис. 97). Биссектриса ВМ, проведенная к основанию равнобедренного треугольника АВС, будет его высотой и медианой, луч СО — биссектриса угла С, 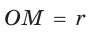
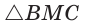
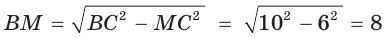
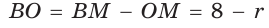
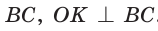
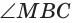
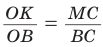
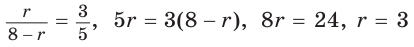
Способ 2 (тригонометрический метод). Из 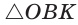
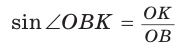
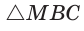
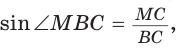
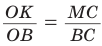
Способ 3 (свойство биссектрисы треугольника). СО — биссектриса 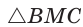
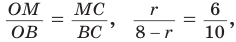
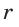
Способ 4 (формула 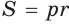
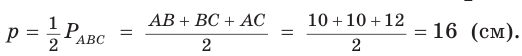
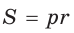
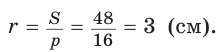
Ответ: 3 см.
Замечание. Из решения ключевой задачи 2 следует свойство: «Центр окружности, вписанной в равнобедренный треугольник, лежит на его высоте, проведенной к основанию».
Верно и обратное утверждение: «Если центр окружности, вписанной в треугольник, лежит на высоте треугольника, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Пример:
Дан равносторонний треугольник со стороной а. Найти радиус R его описанной окружности и радиус 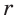
Решение:
Способ 1 (тригонометрический метод).Так как в равностороннем треугольнике биссектрисы являются и высотами, и медианами, то его биссектрисы лежат на серединных перпендикулярах к сторонам треугольника. Поэтому в равностороннем треугольнике центры описанной и вписанной окружностей совпадают.
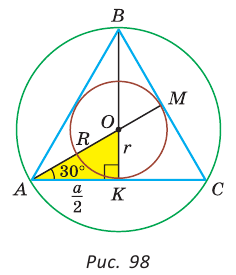
Рассмотрим равносторонний треугольник АВС со стороной а, у которого высоты AM и ВК пересекаются в точке О — центре описанной и вписанной окружностей (рис. 98). Тогда ОА = OB = R — радиусы описанной, 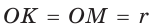
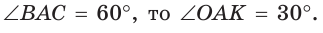
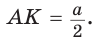
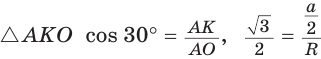
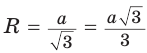
В 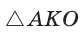
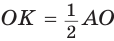
Способ 2 (свойство медиан). Поскольку AM и ВК — медианы треугольника АВС (см. рис. 98), то по свойству медиан 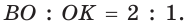
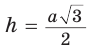
Ответ:
Полезно запомнить!
Поскольку радиус описанной окружности равностороннего треугольника 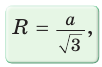
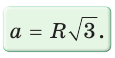
треугольника в 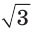
Чтобы найти радиус R описанной окружности равностороннего треугольника, нужно сторону 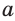
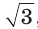
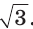
Прямоугольный треугольник и его описанная и вписанная окружности
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а ее радиус равен половине гипотенузы, т. е. 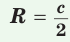
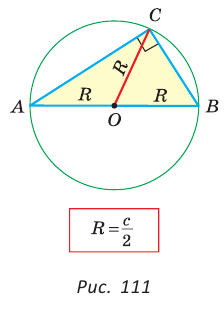
Проведем в прямоугольном треугольнике АВС медиану СО к гипотенузе АВ (рис. 111). Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы, то ОС = ОА = ОВ.
Тогда середина гипотенузы — точка О — равноудалена от точек А, В и С и поэтому является центром описанной окружности треугольника АВС. Радиус этой окружности 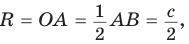
Теорема доказана.
Замечание. Также можно доказать, что серединные перпендикуляры к катетам прямоугольного треугольника пересекаются на середине гипотенузы.
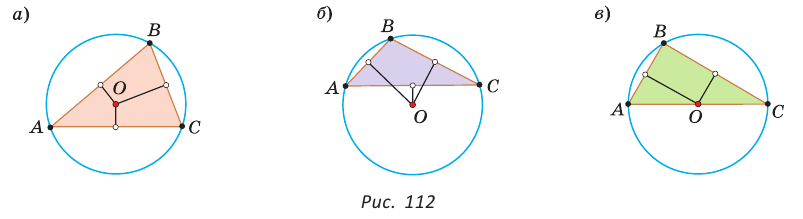
Отметим, что у остроугольного треугольника центр описанной окружности лежит внутри треугольника (рис. 112, а), у тупоугольного — вне треугольника (рис. 112, б), у прямоугольного — на середине гипотенузы (рис. 112, в). Обоснуйте первые два утверждения самостоятельно.
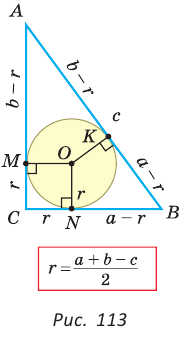
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле 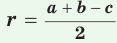
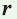
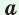
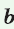
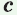
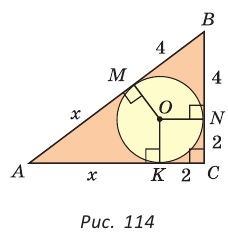
Рассмотрим прямоугольный треугольник АВС с катетами 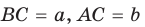
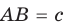
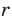
Проведем радиусы в точки касания и получим: 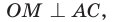
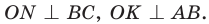
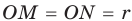
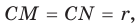
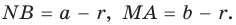
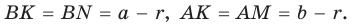
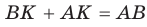
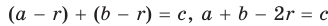
Следствие: 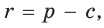
Преобразуем формулу радиуса вписанной окружности:
Формула 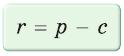
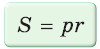
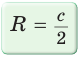
Пример. Дан прямоугольный треугольник, 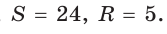
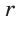
Решение:
Так как 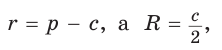
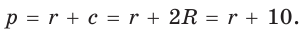
Из формулы 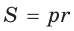
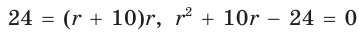
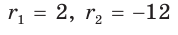
Ответ: 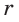
Пример:
Найти радиус окружности, описанной около прямоугольного треугольника, у которого один из катетов равен 6, а радиус вписанной окружности равен 2.
Решение:
Способ 1 (геометрический). Пусть в треугольнике АВС, где 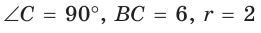
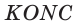
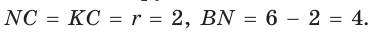
По свойству касательных 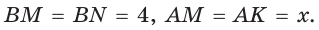
Тогда 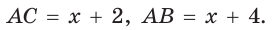
Следовательно, 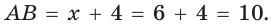
Радиус описанной окружности 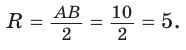
Способ 2 (алгебраический). Подставив в формулу 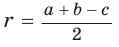
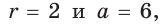
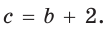
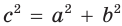
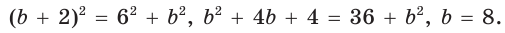
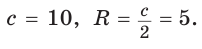
Ответ: 5.
Пример:
Гипотенуза прямоугольного треугольника 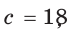
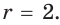
Решение:
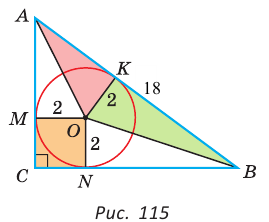
Способ 1 (геометрический). Пусть в 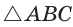
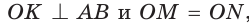
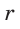
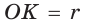
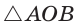
Отсюда 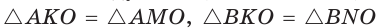
Площадь 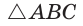
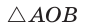
Способ 2 (алгебраический). Из формулы 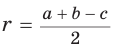
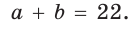
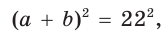
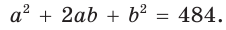
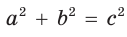
Способ 3 (алгебраический). Из формулы 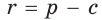
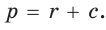
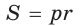
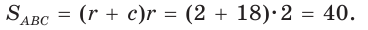
Ответ: 40.
Реальная геометрия:
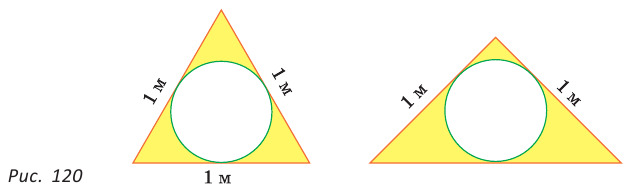
Есть два листа ДСП (древесно-стружечной плиты). Один из них имеет форму равностороннего треугольника со стороной 1 м, другой — форму прямоугольного равнобедренного треугольника с катетами, равными 1 м (рис. 120). Из каждого листа необходимо вырезать по одному кругу наибольшего диаметра. Определите, из какого листа будет вырезан круг большего диаметра и каким в этом случае будет процент отходов, если известно, что площадь круга можно найти по формуле
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанные и описанные четырехугольники
Определение. Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность.
Окружность называется вписанной в многоугольник, если она касается всех его сторон. При этом много угольник называется описанным около окружности.
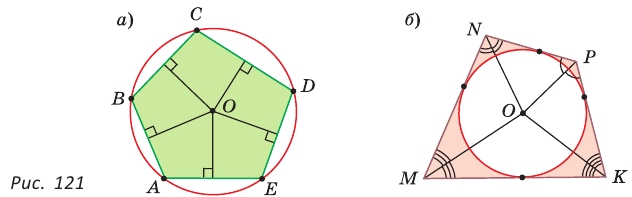
Пятиугольник ABCDE (рис. 121, а) является вписанным в окружность а четырехугольник MNPK (рис. 121, б) — описанным около окружности.
Центр описанной окружности многоугольника находится в точке пересечения серединных перпендикуляров к его сторонам, а центр вписанной — в точке пересечения биссектрис его углов.
Обоснуйте эти утверждения самостоятельно.
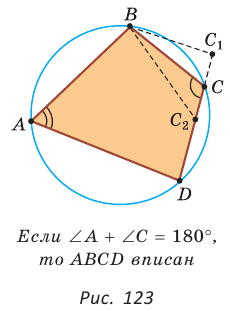
Теорема (свойство вписанного четырехугольника).
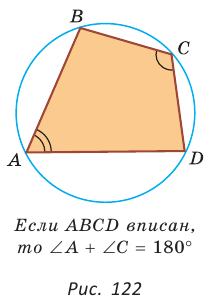
Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°.
Пусть ABCD — четырехугольник, вписанный в окружность (рис. 122). Его углы А, В, С и D являются вписанными в окружность. Так как вписанный угол равен половине дуги, на которую он опирается, то 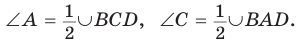
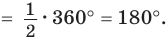
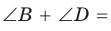
Теорема (признак вписанного четырехугольника).
Если сумма противоположных углов четырехугольника равна 
Рассмотрим четырехугольник ABCD, у которого 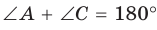
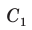
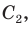
Тогда сумма 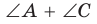
Замечание. Так как сумма углов четырехугольника равна 360°, то для того чтобы около четырехугольника можно было описать окружность, достаточно, чтобы сумма любой пары его противоположных углов была равна 180°.
Следствия.
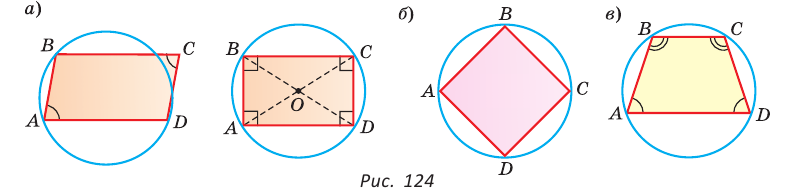
1. Около параллелограмма можно описать окружность, только если этот параллелограмм — прямоугольник (рис. 124, а). Центр этой окружности лежит в точке пересечения диагоналей прямоугольника.
2. Около ромба можно описать окружность, только если этот ромб — квадрат (рис. 124, б).
3. Около трапеции можно описать окружность, только если она равнобедренная (рис. 124, в).
Докажите эти следствия самостоятельно.
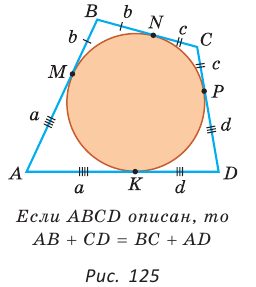
Теорема (свойство описанного четырехугольника ).
Суммы противоположных сторон описанного четырехугольника равны между собой.
Пусть ABCD — описанный четырехугольник, М, N, Р и К — точки касания его сторон с окружностью (рис. 125). Так как отрезки касательных, проведенных к окружности из одной точки, равны между собой, то AM = АК = а, ВМ = BN = b, СР = CN = с, DP = DK = d. Тогда
откуда AD + ВС = AB + CD.
Теорема доказана.
Следствие:
Периметр описанного четырехугольника равен удвоенной сумме длин любой пары его противоположных сторон:
Теорема (признак описанного четырехугольника).
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Пусть для выпуклого четырехугольника ABCD справедливо, что
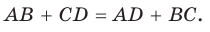
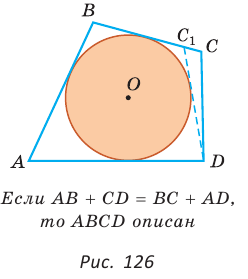
Проведем окружность, которая касается прямых AD, АВ и ВС (рис. 126). Такая окружность существует, ее центр находится в точке пересечения биссектрис углов А и В. Если окружность не касается стороны CD, то либо прямая CD не имеет с окружностью общих точек, либо является секущей. Рассмотрим первый случай. Проведем отрезок 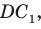
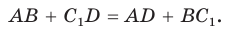
Отняв почленно от равенства (1) равенство (2), получим 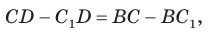
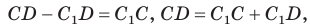
Рассмотрев случай, когда прямая DC — секущая, также придем к противоречию (сделайте это самостоятельно). Следовательно, данная окружность касается стороны CD и в четырехугольник ABCD можно вписать окружность. Теорема доказана.
Следствия.
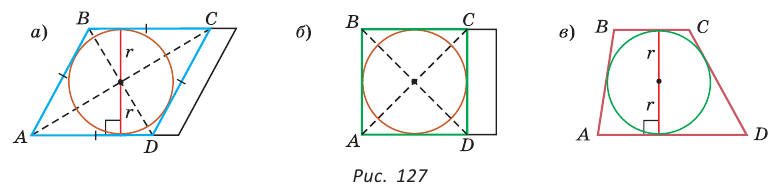
1. В параллелограмм можно вписать окружность, только если этот параллелограмм — ромб. Центр этой окружности лежит в точке пересечения диагоналей ромба, а ее диаметр равен высоте ромба (рис. 127, а).
2. В прямоугольник можно вписать окружность, только если этот прямоугольник — квадрат (рис. 127, б).
3. Диаметр окружности, вписанной в трапецию, равен ее высоте (рис. 127, в).
Докажите эти следствия самостоятельно.
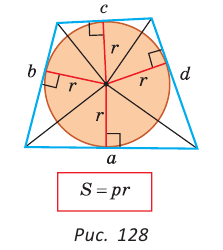
Для описанного многоугольника справедлива формула 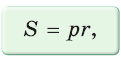
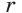
Доказательство аналогично приведенному в § 8 для треугольника. Выполните его самостоятельно, используя рисунок 128.
Пример:
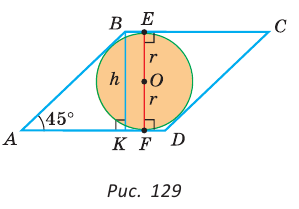
Найти радиус окружности, вписанной в ромб с периметром 24 см и острым углом, равным 45°.
Решение:
Способ 1 (решение прямоугольного треугольника). Пусть ABCD — ромб (рис. 129), О — центр вписанной в ромб окружности. Известно, что высота ВК ромба равна диаметру EF вписанной окружности, т. е. 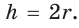
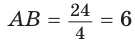
Из прямоугольного треугольника АВК находим. что 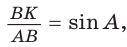
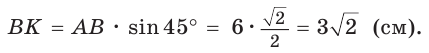
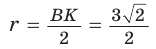
Способ 2 (метод площадей). Ромб — параллелограмм. По формуле площади параллелограмма 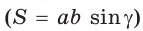
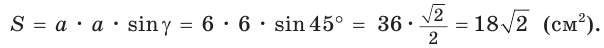
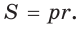
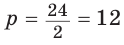
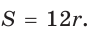
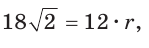
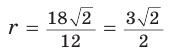
Ответ: 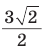
Пример:
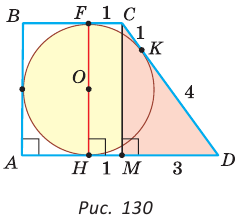
Окружность, вписанная в прямоугольную трапецию ABCD, где 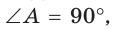
Решение:
Способ 1. Площадь трапеции находится по формуле 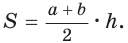
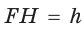
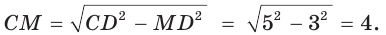
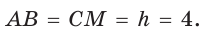
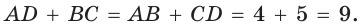
Способ 2*. Центр О вписанной окружности лежит на пересечении биссектрис углов 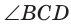
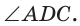
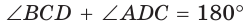
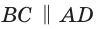
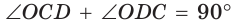
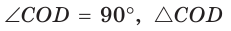
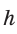
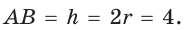
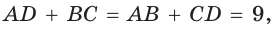
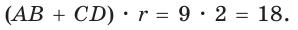
Ответ: 18.
Замечание. Полезно запомнить свойство: «Боковая сторона описанной трапеции видна из центра вписанной окружности под углом 90°».
Пример:
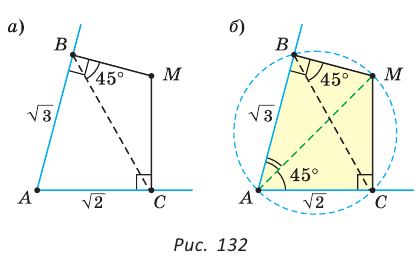
Внутри острого угла А взята точка М, из которой опущены перпендикуляры МВ и МС на стороны угла А, 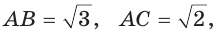
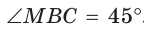
Решение:
Так как в четырехугольнике АВМС сумма углов В и С равна 180°, то около него можно описать окружность. Проведем в ней хорду AM (рис. 132, б). Поскольку 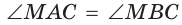
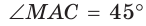
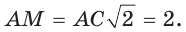
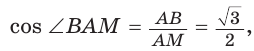
Окружность, вписанная в треугольник
Пример:
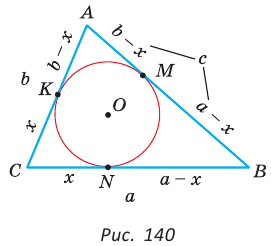
Окружность вписана в треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с. Вывести формулу для нахождения длин отрезков, на которые точки касания окружности со сторонами делят каждую сторону треугольника.
Решение:
Пусть К, М и N — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника АВС (рис. 140). Известно, что отрезки касательных, проведенных из одной точки к окружности, равны между собой.
Тогда, если 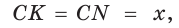
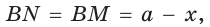
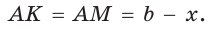
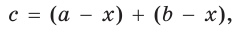
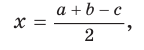
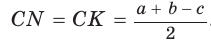
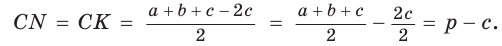
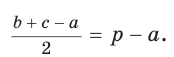
Ответ:
Замечание. Если 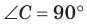
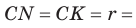
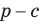
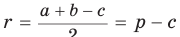
Описанная трапеция
Пример:
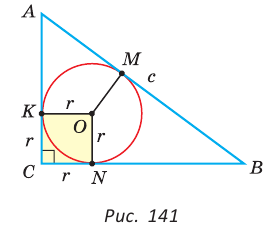
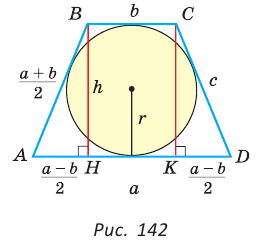
Найти площадь описанной равнобедренной трапеции с основаниями а и Ь.
Решение:
Площадь трапеции можно найти по формуле 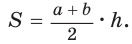
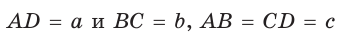
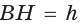
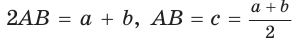
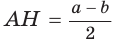
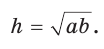
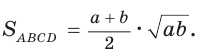
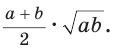
Замечание. Площадь описанной равнобедренной трапеции равна произведению среднего арифметического и среднего геометрического ее оснований.
Полезно запомнить!
Для описанной равнобедренной трапеции с основаниями 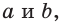
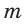
Дополнительные свойства и признаки вписанного четырехугольника
Теорема.
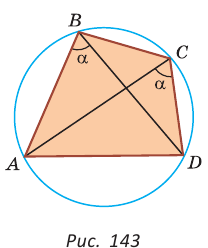
Около четырехугольника можно описать окружность тогда и только тогда, когда угол между его стороной и диагональю равен углу между противоположной стороной и другой диагональю.
Рис. 143
1. Если четырехугольник ABCD вписан в окружность (рис. 143), то 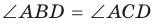
2. Докажем, что если в некотором четырехугольнике ABCD 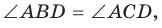
Опишем около треугольника ABD окружность.
В 8-м классе (В. В. Казаков. «Геометрия, 8», с. 186) было доказано свойство:
«Геометрическим местом точек плоскости, из которых данный отрезок AD виден под углом а, является объединение двух дуг окружностей: дуги ABD и ей симметричной относительно прямой AD, исключая точки 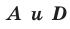
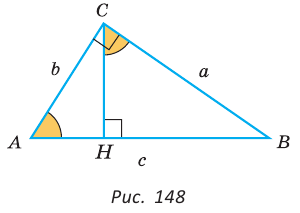
Обобщенная теорема Пифагора
В прямоугольном треугольнике 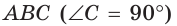
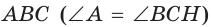
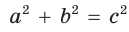
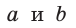
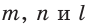
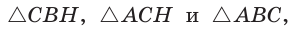
Действительно, из подобия указанных треугольников 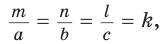
Пример:
Пусть 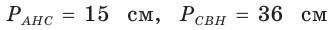
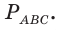
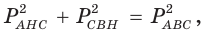
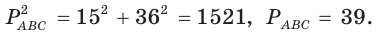
Ответ: 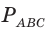
Формула Эйлера для окружностей
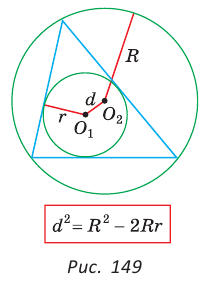
Для вписанной и описанной окружностей треугольника с радиусами 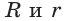
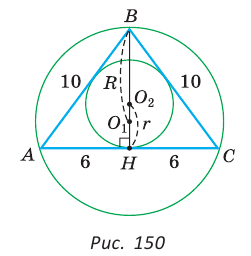
Проверим справедливость этой формулы на примере равнобедренного треугольника АВС, у которого АВ = ВС = 10, АС = 12 (рис. 150).
Вначале найдем расстояние между центрами указанных окружностей традиционным способом.
Проведем высоту ВН, длина которой будет равна 8 (пифагорова тройка 6, 8, 10). Центры описанной и вписанной окружностей — соответственно точки 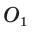
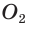
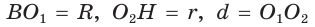
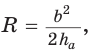
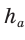
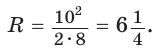
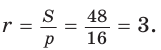
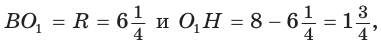
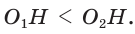
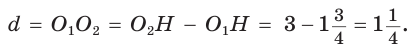
А теперь найдем d по формуле Эйлера:
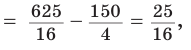
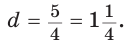
Запомнить:
- Центр описанной окружности треугольника (многоугольника) лежит в точке пересечения серединных перпендикуляров к его сторонам.
- Центр вписанной окружности треугольника (многоугольника) лежит в точке пересечения биссектрис его углов.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, а ее радиус равен половине гипотенузы:
- Радиус вписанной окружности прямоугольного треугольника находится по формуле
- Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°. И обратно.
- Если четырехугольник описан около окружности, то суммы его противоположных сторон равны между собой. И обратно.
- Площадь треугольника и описанного многоугольника можно найти по формуле
где
— полупериметр,
— радиус вписанной окружности.
Справочная информация по описанной и вписанной окружности треугольника
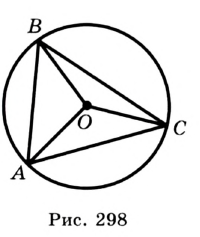
Определение. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.
На рисунке 298 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность. Очевидно, что центр описанной окружности треугольника равноудален от всех его вершин. На рисунке 298 точка 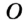
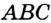
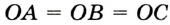
Теорема 21.1. Вокруг любого треугольника можно описать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 
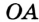
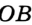
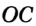
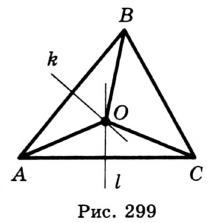
На рисунке 299 изображен произвольный треугольник 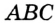
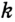
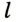
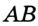
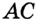
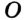

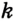
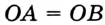
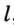
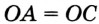
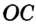

Заметим, что вокруг треугольника можно описать только одну окружность. Это следует из того, что серединные перпендикуляры 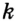
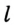
Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Следствие 2. Центр описанной окружности треугольника — это точка пересечения серединных перпендикуляров его сторон.
Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон.
На рисунке 300 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
Точка 
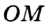
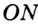
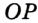
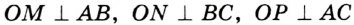
Теорема 21.2. В любой треугольник можно вписать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника 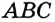
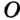
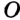
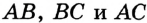
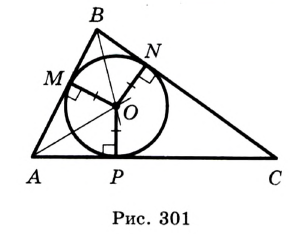
На рисунке 301 изображен произвольный треугольник 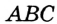


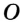


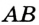
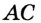


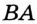
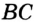

Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов 

Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке.
Следствие 2. Центр вписанной окружности треугольника — это точка пересечения его биссектрис.
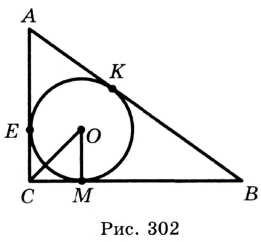
Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле 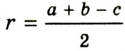
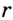
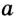
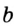
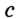
Решение:
В треугольнике 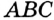
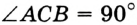
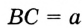
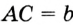
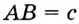
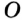
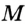
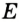
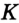
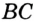
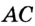
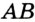
Отрезок 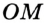
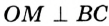
Так как точка 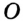
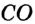
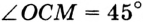
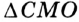
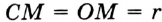
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Первый признак равенства треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Геометрия
План урока:
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Понятие правильного многоугольника
У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.
Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.
Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.
Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:
Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:
Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:
Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?
Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:
Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?
Решение. В формулу
Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?
Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:
Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Описанная и вписанная окружности правильного многоугольника
Докажем важную теорему о правильном многоуг-ке.
Для доказательства обозначим вершины произвольного правильного n-угольника буквами А1, А2, А3…Аn. Далее проведем биссектрисы углов ∠А1 и ∠А2. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА3, ОА4 и т. д.
∠А1 и ∠А2 одинаковы по определению правильного многоуг-ка:
Из этого факта вытекает два равенства:
Получается, что ОА3 – это также биссектриса ∠А3. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):
Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:
Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А1, А2 и А3, можно провести только одну окружность, ч. т. д.
Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА1А2, ∆ОА2А3, ∆ОА3А4, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН1, ОН2, ОН3… на стороны многоуг-ка.
Так как высоты проведены в равных треуг-ках, то и сами они равны:
Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН1. Он должен будет пройти и через точки Н2, Н3, … Нn. Причем отрезки ОН1, ОН2, ОН3 окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:
Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А1, ∠А2, ∠А3, то есть в точке О. Так как расстояние от О до А1А2 – это отрезок ОН1, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.
Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.
Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН1, ОН2, ОН3,… проведены в равнобедренных треуг-ках∆ОА1А2, ∆ОА2А3, ∆ОА3А4,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н1, Н2, Н3,… – это середины сторон многоуг-ка.
Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?
Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.
Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы для правильного многоугольника
Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой an, где n– число сторон у многоуг-ка. Например a4– это сторона квадрата, a6– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.
Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу
для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.
Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:
Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:
С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).
Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.
Решение. Запишем следующую формулу:
Это равенство как раз и надо было доказать в этом задании.
Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.
Решение. Запишем формулу:
Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.
Найдем периметр шестиугольника:
Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?
Решение. Зная периметр треуг-ка, легко найдем и его сторону:
Далее вычисляется радиус описанной около треугольника окружности:
Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?
Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:
Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:
Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:
В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:
Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:
∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:
AH = AC/2 = 17/2 = 8,5 мм
Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:
Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.
Видео:Радиус описанной окружностиСкачать

Построение правильных многоугольников
При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.
Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:
На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а6. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а6. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.
Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.
Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.
Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:
Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.
Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.
В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Формулы вписанной и описанной окружности для треугольника и квадрата
Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность
Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
- Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
- В любой треугольник можно вписать окружность, и только одну.
- Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра: $$r = frac
$$ , где S — площадь треугольника, а $$p =frac$$ — полупериметр треугольника.
Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.
Окружность называется описанной около треугольника, если она проходит через три его вершины.
- Вокруг любого треугольника можно описать окружность, и только одну.
- В любом треугольнике сторона равна произведению диаметра описанной окружности и синуса противолежащего угла.
- Площадь треугольника равна отношению произведения длин всех его сторон к учетверенному радиусу окружности, описанной около этого треугольника: $$R =frac$$, где S — площадь треугольника.
- Центр вневписанной окружности лежит на пересечении биссектрис внешних углов, при вершинах касаемой стороны, и биссектрисы угла при третей вершине.
Окружность, вписанная в прямоугольный треугольник
- Радиус вписанной окружности находят по формулам: $$r = frac$$, и $$r = frac$$, где a и b катеты прямоугольного треугольника, а c гипотенуза прямоугольного треугольника.
Окружность, описанная около прямоугольного треугольника
- Центр описанной окружности совпадает с серединой гипотенузы.
- Радиус равен половине гипотенузы: $$R = frac$$.
- Радиус равен медиане, проведенной к гипотенузе: $$R = m_$$.
Четырехугольник, вписанный в окружность
- Четырехугольник можно вписать в окружность, если сумма противолежащих углов равна $$180^circ: alpha + beta + gamma +delta = 180^circ$$.
- Если четырехугольник вписан в окружность, то суммы противолежащих углов равны $$180^circ$$.
- Сумма произведений противолежащих сторон четырехугольника ABCD равна произведению диагоналей: $$ABcdot DC + AD cdot BC = BD cdot AC$$.
- Площадь: $$S = sqrt$$, где $$p = frac$$ — полупериметр четырехугольника.
Окружность, вписанная в ромб
- В любой ромб можно вписать окружность.
- Радиус r вписанной окружности: $$r = frac$$, где h — высота ромба или $$r = frac <d_cdot d_>$$, где a — сторона ромба, d1 и d2 — диагонали ромба.
🔍 Видео
Геометрия. 9 класс. Формулы для нахождения радиусов вписанной и описанной окружностей треугольникаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Вписанные и описанные окружности (в треугольник)Скачать

Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

R и r для квадрата. Как вывести формулы радиуса вписанной и описанной окружностей для квадрата.Скачать

ОГЭ. Задача на описанную окружность № 16. Как легко решить задачуСкачать

Геометрия. ОГЭ по математике. Задание 16Скачать

8 класс, 38 урок, Вписанная окружностьСкачать

Формулы для радиусов вписанной и описанной окружностей треугольника Геометрия 9классСкачать

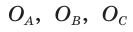
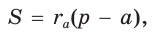
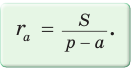
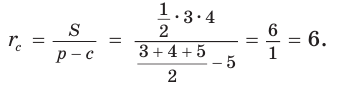
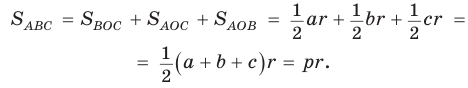
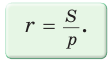
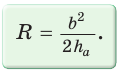
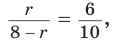
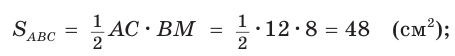
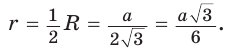
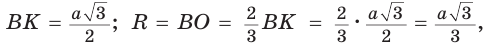
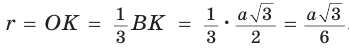
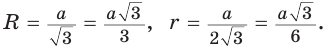
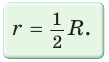
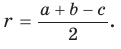
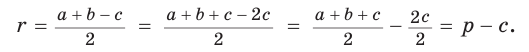
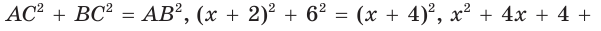
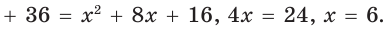
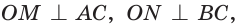
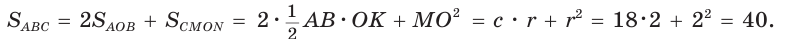
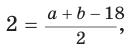
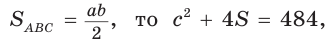
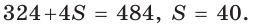
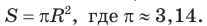

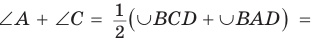
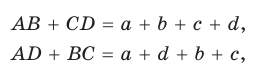
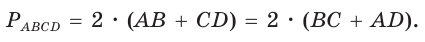
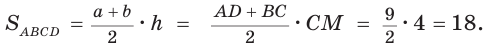
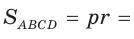
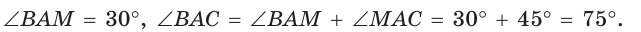
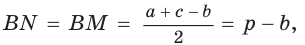
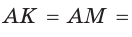
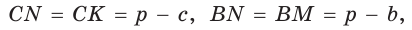
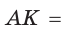
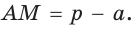
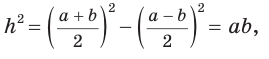
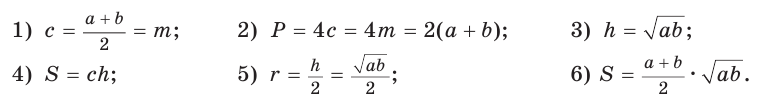
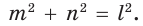
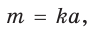
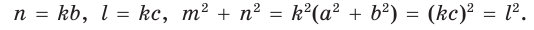
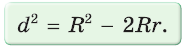
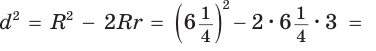
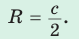
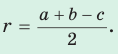
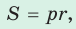 где
где 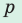 — полупериметр,
— полупериметр, 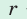 — радиус вписанной окружности.
— радиус вписанной окружности.