Протон и альфа частица окружности

Протон в однородном магнитном поле между полюсами магнита под действием силы Лоренца движется по окружности радиусом r. В этом же поле по окружности с таким же радиусом стала двигаться α-частица. Как изменились период обращения в магнитном поле и модуль импульса α-частицы по сравнению с протоном?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

При движении заряженной частицы в однородном магнитном поле по окружности параметры системы связаны между собой соотношениями

Значит, радиус обращения частицы равен А скорость частицы равна Модуль импульса частицы будет равен

Период обращения равен Заряд альфа-частицы в два раза больше заряда протона, а её масса в четыре раза больше массы протона, следовательно, период обращения альфа-частицы в два раза больше, чем у протона, её импульс также в два раза больше, чем у протона.

Видео:Химия| Элементарные частицы. Протоны. Нейтроны. Электроны.Скачать

Протон и альфа частица окружности

Задание 17. Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью а-частица, центростремительное ускорение а-частицы и период её обращения по сравнению с протоном должны:

3) не измениться

На заряженную частицу (протон) со стороны магнитного поля действует сила Лоренца , где q – заряд частицы; v – скорость частицы; B – напряженность магнитного поля. Так как протон движется по окружности, то магнитное поле направлено перпендикулярно его движению, то есть и сила Лоренца в данном случае запишется в виде

.

В соответствии со вторым законом Ньютона, силу Лоренца также можно записать как

, (1)

где — центростремительное ускорение. Получаем значение для радиуса окружности R:

Теперь вычислим изменение радиуса окружности для альфа-частицы, движущейся с той же скоростью. Альфа-частица имеет в своем составе два протона и два нейтрона, то есть ее масса в 4 раза больше массы протона, а заряд в 2 раза больше заряда протона. В итоге получаем:

,

то есть радиус окружности увеличится в 2 раза.

Период обращения – это время, за которое альфа-частица сделает один полный круг. Так как радиус увеличился в 2 раза, а скорость осталась прежней, то период обращения увеличится.

Для центростремительного ускорения альфа-частицы из (1) имеем формулу:

,

то есть центростремительное ускорение уменьшается в 4 раза по сравнению с центростремительным ускорением протона.

Видео:ЕГЭ Сила Лоренца Задание 6 #7Скачать

Протон и альфа-частица (4He2), ускоренные одинаковой разностью потенциалов, влетают

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Условие задачи:

Протон и альфа-частица ((_2^4<text>)), ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле перпендикулярно линиям индукции. Как связаны между собой радиусы окружностей (R_1) и (R_2), по которым будут двигаться, соответственно, протон и альфа-частица (массы нейтрона и протона считать равными)?

Задача №8.2.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Видео:А - Альфа частицыСкачать

Решение задачи:

Для начала определимся с массами и зарядами. Протон имеет массу (m_p) и модуль заряда (e). Альфа-частица (ядро атома гелия) (_2^4<text>) состоит из двух протонов и двух нейтронов. Поэтому, если считать массы нейтрона и протона считать равными, её масса приближенно (!) равна (4m_p), а модуль заряда равен (2e).

Если заряженная частица была ускорена разностью потенциалов (U), её скорость (upsilon) можно найти по закону сохранения энергии:

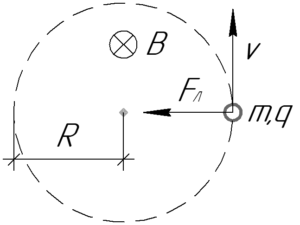
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца (F_Л), которую определяет следующая формула:

Здесь (B) – индукция магнитного поля, (upsilon) – скорость частицы, (q) – модуль заряда частицы, (alpha) – угол между вектором скорости и вектором магнитной индукции.

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. Мы в этой задаче имеем дело с положительно заряженными частицами, тогда в нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца будет направлена влево.

Сила Лоренца (F_Л) сообщает частице центростремительное ускорение (a_ц), поэтому из второго закона Ньютона следует, что:

Центростремительное ускорение (a_ц) можно определить через скорость (upsilon) и радиус кривизны траектории (R) по формуле:

Подставим (4) в (3), тогда:

Приравняем правые части (2) и (5):

Откуда радиус траектории (R) равен:

Учтём ранее полученное выражение (1):

Запишем формулу для определения радиуса траектории протона и альфа-частицы (касаемо их зарядов и масс читайте первый абзац решения):

Разделим нижнее равенство на верхнее, тогда:

Видео:Загадка радиуса протона: в чём она состоит и как мы её разгадали?Скачать

Ответ: (frac<<>><<>> = sqrt 2).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

💡 Видео

Мельчайшие частицы | Кварки, лептоны и бозоныСкачать

Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Как выглядит протон?Скачать

Альфа частица движется по окружности в однородном магнитном полеСкачать

189. Альфа - частица.Скачать

Протон как составная частицаСкачать

Движение заряженной частицы в магнитном поле | 16 задание ЕГЭ | Магнитные поля в ЕГЭ по физикеСкачать

Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по - №24993Скачать

Физика Протон движется в однородном магнитном поле с магнитной индукцией 20 мТл по окружностиСкачать

Урок 223 (осн). Альфа- и бета-распад. Правила Содди.Скачать

Урок 277. Масс-спектрограф. Циклотрон. Магнитный щит ЗемлиСкачать

Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Физика элементарных частиц – курс Дмитрия Казакова / ПостНаукаСкачать

Физика - Магнитное полеСкачать

Урок 470. Открытие нейтрона. Протонно-нейтронная модель ядраСкачать