| Учебный курс | Решаем задачи по геометрии |
В этом уроке приведены определение и свойства правильной треугольной пирамиды и ее частного случая — тетраэдра (см. ниже). Ссылки на примеры решения задач приведены в конце урока. Содержание Видео:оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How to make Paper PyramidСкачать  ОпределениеПравильная треугольная пирамида — это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.
На рисунке обозначены: Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже). Видео:Построение проекции пирамиды. Метод прямого треугольника.Скачать  Свойства правильной треугольной пирамиды:
Формулы для правильной треугольной пирамидыФормула объема правильной треугольной пирамиды:
V — объем правильной пирамиды, имеющей в основании правильный (равносторонний) треугольник Поскольку правильная треугольная пирамида является частным случаем правильной пирамиды, то формулы, которые верны для правильной пирамиды, верны и для правильной треугольной — см. формулы для правильной пирамиды. Примеры решения задач: Видео:Развертка тетраэдра - это легко! Как сделать объёмную правильную треугольную пирамиду из бумаги?Скачать  ТетраэдрЧастным случаем правильной треугольной пирамиды является тетраэдр. Тетраэдр — это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.
Медиана тетраэдра — это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине) Бимедиана тетраэдра — это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра) Высота тетраэдра — это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности). Тетраэдр обладает следующими свойствами:
Видео:Треугольная пирамида. Ортогональные и изометрическая проекции.Урок22.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать  Пирамида. Правильная пирамидаЭтот видеоурок доступен по абонементуУ вас уже есть абонемент? Войти
Данный видеоурок поможет пользователям получить представление о теме Пирамида. Правильная пирамида. На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение. Рассмотрим, что такое правильная пирамида и какими свойствами она обладает. Затем докажем теорему о боковой поверхности правильной пирамиды. Видео:Развертка пирамидыСкачать  ПирамидаПирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д. Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания. Основание — многоугольник, которому не принадлежит вершина пирамиды. Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Видео:Усеченная пирамида. 11 класс.Скачать 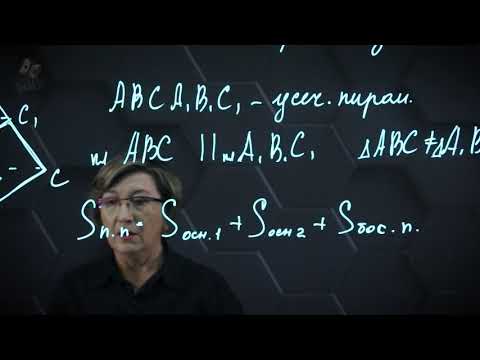 Некоторые свойства пирамиды1) Если все боковые ребра равны, то – около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное. Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны. Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны. 2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное. Видео:Основание пирамиды SABC-равносторонний треугольник АВС. Боковое ребро SA перпендикулярноСкачать  Виды пирамидПирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо: – боковые ребра правильной пирамиды равны; – в правильной пирамиде все боковые грани — равные равнобедренные треугольники; – в любую правильную пирамиду можно вписать сферу; – около любой правильной пирамиды можно описать сферу; – площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. Видео:Делаем модель пирамиды для решения задачи по стереометрииСкачать  |
