Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):
Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
Разделим результат на число Пи и запишем ответ.
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.
Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см 2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см 2 .
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.
Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
Выразим площадь большего круга, так как его радиус равен 6х:
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см 2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см 2 .
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.
Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3 ∙ х, то
Выразим площадь большего круга. Так как его радиус равен 4 ∙ х, то
Разделим площадь большего на площадь меньшего:
То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см 2 .
Вычислим радиус меньшего круга. Его площадь равна 9, значит,
Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:
Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:
Определяем площадь большего круга:
Находим разность: 16 – 9 = 7 см 2
На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.
В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?
По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.
Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
С уважением, автор проекта Александр Крутицких.
- На плоскости нарисовано несколько окружностей
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- ИЗОБРАЖЕНИЕ ОКРУЖНОСТИ В ПЕРСПЕКТИВЕ.
- Перспектива окружности в горизонтальной плоскости.
- Упражнение 1.
- Упражнение 2.
- Перспектива окружности в вертикальной или наклонной плоскости.
- Перспективные зарисовки с натуры.
- Рисунок с натуры коробки или книжки.
- Упражнение 4
- Упражнение 5
- РИСУНОК С НАТУРЫ КРУЖКИ.
- Упражнение 6
- Упражнение 7.
- На листе бумаги нарисованы отрезки двух лучей, образующих угол, вершина которого лежит вне листа. С помощью циркуля и линейки
- Ваш ответ
- Похожие вопросы
Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

На плоскости нарисовано несколько окружностей
Видео:Окружность и круг, 6 классСкачать

Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:1 2 4 сопряжение окружностейСкачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | ||||||||||||||
| Внутренняя касательная к двум окружностям | ||||||||||||||
| Внутреннее касание двух окружностей | ||||||||||||||
| Окружности пересекаются в двух точках | ||||||||||||||
| Внешнее касание двух окружностей | ||||||||||||||
| Каждая из окружностей лежит вне другой | ||||||||||||||
| Фигура | Рисунок | Формула |
| Внешняя касательная к двум окружностям |  |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
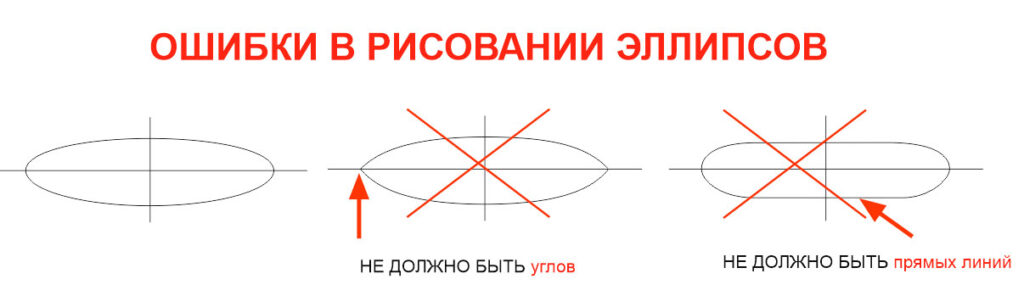
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Длина окружности. Площадь круга - математика 6 классСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать  ИЗОБРАЖЕНИЕ ОКРУЖНОСТИ В ПЕРСПЕКТИВЕ.Видео:Деление окружности на равные части с помощью циркуляСкачать  Перспектива окружности в горизонтальной плоскости.Множество предметов, находящихся вокруг нас, имеют формы, очертанием которых является окружность. Чаще всего эта окружность находится в горизонтальной плоскости: это могут быть края чашки, стоящей на столе или табуретка с круглым сидением. Если такая окружность находится на уровне наших глаз, на линии горизонта, мы видим ее как прямую линию. Если мы смотрим на окружность сверху, то мы видим ее без искажений, как окружность. Во всех остальных случаях, когда окружность располагается в горизонтальной плоскости, мы видим ее как эллипс.* То есть, как лекальную кривую, симметричную относительно двух взаимно перпендикулярных осей. При чем, одна из этих осей ВСЕГДА строго вертикальна, а другая, соответственно, горизонтальна. *Строго говоря, изображение окружности в перспективе не является эллипсом, так как дальняя от нас его часть чуть меньше, чем ближняя. И, соответственно, он не симметричен относительно горизонтальной оси. Соотношение между длинами осей эллипса называют раскрытием. Грубо говоря, чем больше эллипс похож на круг, тем более он раскрытый. В изображении эллипсов в горизонтальной плоскости есть два основных правила:
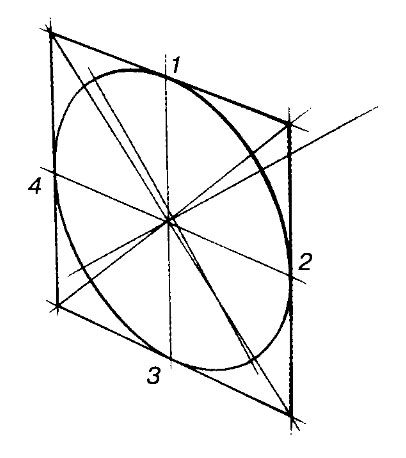
Легко понять, почему это так , построив в перспективе окружность вписанную в квадрат. Видео:Радиус и диаметрСкачать  Упражнение 1.Постройте окружность тем же способом, с той же точкой схода, но выше линии горизонта. Выделите более толстой линией ее передний край. ОБРАТИТЕ ВНИМАНИЕ что в рисунке окружности, лежащие в горизонтальной плоскости мы НЕ строим с помощью описанного квадрата. Так как этот даёт искажения, если точка схода для квадрата не лежит на вертикальной оси эллипса. Мы проводим две оси эллипса и задаем степень раскрытости на глаз, но учитываем положение эллипса относительно линии горизонта и других эллипсов. Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать  Упражнение 2.На рисунках изображена последовательность построения цилиндра и конуса. Нарисуйте цилиндры и конусы выше и ниже линии горизонта . Раскрытие эллипсов задаём на глаз. Окружность в квадрат не вписываем. Видео:МЕРЗЛЯК-6. КРУГ И ОКРУЖНОСТЬ. ПАРАГРАФ-24Скачать  Перспектива окружности в вертикальной или наклонной плоскости.С окружностями в вертикальной плоскости нам приходится иметь дело достаточно часто. Например, рисуя арки в архитектуре. Самый простой случай — когда окружность находится в плоскости параллельной картинной. Тогда мы видим ее без искажений.
Если окружность находится под углом к картине, для построений мы также используем описанный квадрат. Этот способ применяется как в черчение, так и в рисунке, так как на глаз нарисовать окружность в таком ракурсе очень сложно . В этом курсе мы только знакомимся со способом построения окружности в вертикальной плоскости. Но если у вас есть желание, подробно об этом можно прочитать в учебнике Осмоловской (ст. 26) или, в упрощенном виде у Шарова и Барщ. Видео:✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать  Перспективные зарисовки с натуры.Мы закончили блок теории построений. Теперь начинаем работать с натуры. На этом этапе важно осознать, что рисунок — не черчение. В рисунке мы не пользуемся линейкой, редко строим точки схода на дополнительном листе. Наша задача, зная, какие построения применялись бы для перспективного чертежа, сделать минимум из них на глаз так, чтобы в результате получилось убедительное изображение, соответствующее основным правилам перспективы. Рисование с фотографии. Я вас очень прошу, по крайней мере на начальном этапе не срисовывать с фотографии, даже называя это рисованием с референсов. Рисуя с фото вы НЕ развиваете пространственное воображение и умение на плоскости изображать объем. Вы только учитесь копировать с одного листа на другой пятна тона. Это, конечно, тоже полезный навык но для хорошего рисунка его не достаточно. Постановка натуры. Правильная постановка натуры помогает избежать многих ошибок в рисунке и делает работу легче и приятнее. Поэтому я очень прошу вас уделить этому внимание.
Видео:Деление окружности на 3; 6; 12 равных частейСкачать  Рисунок с натуры коробки или книжки.
Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать  Упражнение 4Нарисуйте с натуры предмет с прямыми ребрами ( книжку, коробку и т. п.) Мы НЕ рисуем с фото, мы НЕ копируем рисунок, разобранный выше. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Упражнение 5Нарисуйте два предмета с прямыми ребрами, один из которых стоит на другом. Видео:Задачи из ОГЭ. Задания 1-5. Вебинар | МатематикаСкачать  РИСУНОК С НАТУРЫ КРУЖКИ.Для постановки нужно выбрать кружку простой цилиндрической формы, с ручкой. Саму кружку мы видим без сокращений, поэтому отношение высоты и ширины можно измерить, приложив карандаш непосредственно к натуре.
Видео:Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать  Упражнение 6Нарисуйте кружку с натуры. Видео:Как начертить овал. Эллипс вписанный в ромбСкачать  Упражнение 7.Нарисуйте ту же кружку в другом ракурсе по представлению(не глядя на натуру) Видео:Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать  На листе бумаги нарисованы отрезки двух лучей, образующих угол, вершина которого лежит вне листа. С помощью циркуля и линейкиВидео:Построение пятиугольника циркулемСкачать  Ваш ответВидео:Что такое круг окружность радиусСкачать  Похожие вопросы
Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. |

























































 View of the Tiber with the Castel Sant’Angelo
View of the Tiber with the Castel Sant’Angelo