В выпуклом четырехугольнике диагонали пересекаются под углом 60

Видео:№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать

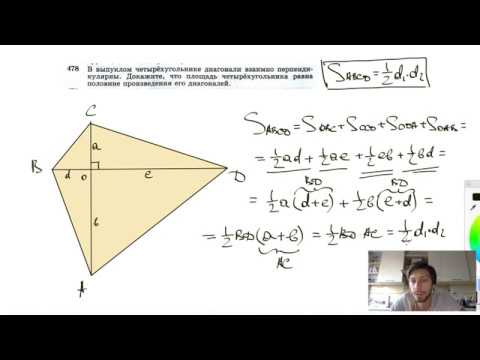
Ваш ответ

Видео:Геометрия Признак параллелограмма: Если в четырехугольнике диагонали точкой пересечения делятсяСкачать

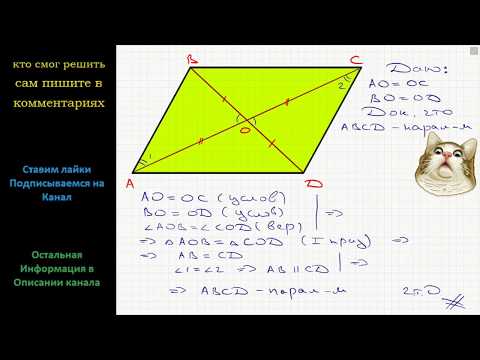
решение вопроса

Видео:Площадь четырёхугольника через диагоналиСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,688
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

В выпуклом четырехугольнике диагонали пересекаются под углом 60

Вопрос по геометрии:

В выпуклом четырехугольнике отрезки, соединяющие середины противоположных сторон, равны соответственно x и y и пересекаются под углом 60. Найдите диагонали четырехугольника

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Смотри вложение:
* Если картинка обрывается, уменьшить экран надо [ctrl -(минус)] или скачать

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Найдите углы четырёхугольникаСкачать

Презентация задач по планиметрии второй части профильного ЕГЭ (С4)

Видео:№403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Решение задач С4

Содержание Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 (теорема) Задача 13 Задача 14 Задача15

1. В прямоугольном треугольнике ABC гипотенуза АВ равна c и ∠ABC=α.Найдите все медианы в этом треугольнике. Р е ш е н и е. Поскольку медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, медиана CM равна . Пусть K– середина BC.Тогда CK= BC= AB*cosα= *c*cos α.По теореме Пифагора из прямоугольного треугольника ACK находим, что AK= = = = = = = Аналогично находим медиану BN.

2. В треугольнике ABC проведена медиана BM. Известно, что . Найдите отношение . Р е ш е н и е. На продолжении медианы BM за точку M отложим отрезок MD, равный BM. Диагонали AC и BD четырёхугольника ABCD делятся точкой пересечения M пополам, значит, ABCD – параллелограмм. Поэтому AB=BC и ∠ADB= ∠CBM. По теореме синусов из треугольника ABD находим, что Следовательно,

3. В выпуклом четырёхугольнике ABCD отрезки, соединяющие середины противоположных сторон, пересекаются под углом 60˚,а их длины относятся как 1:3. Чему равна меньшая диагональ четырёхугольника ABCD, если большая равна . Р е ш е н и е. Середины сторон любого четырёхугольника являются вершинами параллелограмма, стороны которого параллельны диагоналям четырёхугольника и соответственно равны их половинам. Обозначим через x и 3x половины диагоналей параллелограмма. Поскольку угол между ними равен 60˚, то по теореме косинусов квадраты сторон параллелограмма равны x²+9x²-3x²=7x² , x²+9x²+3x²=13x² Поскольку большая диагональ четырёхугольника равна , большая сторона параллелограмма равна , т. е. 13х²= , откуда x= . Тогда меньшая сторона параллелограмма равна . Следовательно, меньшая диагональ данного четырёхугольника равна

4. Найдите площадь трапеции с основаниями 18 и 13 и боковыми сторонами З и 4. Р е ш е н и е. Через вершину С меньшего основания ВС трапеции АВСD (ВC=13, АD=18, АВ=4, СD=3) проведём прямую, параллельную боковой стороне АВ, до пересечения с основанием АD в точке К. Тогда СК=АВ=4, DK=АD — АК=АD — ВС=18 — 13=5, СD=З. Треугольник КСD прямоугольный, так как КD²=СD²+СК². Его высота, опущенная на гипотенузу, равна . Следовательно, SABCD

5. Две стороны треугольника равны З и 6, а угол между ними ра 60°. Найдите биссектрису треугольника, проведённую из верши этого угла. Решение. Пусть АD — биссектриса треугольника АВС, в котором АВ =6, АС =3, ∠ВАС=60°. Первый способ. Обозначим AD=x. Тогда SABC= SABC=SABC+SACD= = Из уравнения находим, что x=2 Второй способ. Заметим, что треугольник АВС прямоугольный. Тогда треугольник ACD также прямоугольный, причём САD =30°. Следовательно, AD=AC:cos∠CAD=3:cos30°=2

6. Отношение отрезков Точки M и N – середины сторон соответственно BC и CD параллелограмма ABCD. Отрезки AM и BN пересекаются в точке O. Найдите отношение .

Решение: 1.Пусть продолжения BN и AD пересекаются в точке E. И пусть BM=MC=a.Тогда BC=AD=2a. 2. DNE= CNB по двум углам и стороне между ними а) CN=ND (по условию) б) CNB= DNE (как вертикальные) в) EDN= BCN (как соответственные) => DE=BC=2a. 3. AE=AD+DE=4a. 4. BOM

EOA (по 3 углам) 5. = = = B a M a C O N A 2a D

7. Отношение площадей. В треугольнике ABC медиана AD и биссектриса BE перпендикулярны и пересекаются в точке F. Известно, что площадь треугольника DEF равна 5. Найдите площадь треугольника ABC.

Решение: 1) ABD равнобедренный, так как биссектриса BF — высота => AF=FD 2) AFE= DFE (по углу и двум сторонам) => = = 5 3) BC = 2BD = 2BA, тогда = = 2 (по св-ву биссектрисы) 4) = 2 = 4 =20 5) = + = 10 + 20 = 30 6) = = 1 => = = 30 7) = 60

8. Касательная к окружности Из точки M, лежащей вне окружности с центром O и радиусом R, проведены касательные MA и MB (A и B – точки касания). Прямые OA и MB пересекаются в точке C. Найдите OC, если известно, что отрезок OM делит окружность пополам.

Решение: 1) Пусть K – точка пересечения окружности с отрезком OM. Тогда OM = 2OK = 2R 2) В OAM ( MAO= ) катет OA меньше гипотенузы в 2 раза OM => AMO = 3) AMC= (т.к. MO – биссектриса AMC) 4) Из MAC ( MAC= ) : ACM = => COM – равнобедренный => OM= MO= 2R ∆ ∆ ∆

9. Касающиеся окружности Окружности с центрами и касаются внешним образом в точке C. Прямая касается этих окружностей в различных точках A и B соответственно. Найдите угол A B, если известно, что tg ABC = .

Решение: 1) Проведём общую касательную из точки C 2) Пусть она пересекает прямую AB в точке M => MA=MC=MB => ABC = 90 3) Опустим перпендикуляр H на её хорду CB, тогда CH=HB 4) т.к. tg ABC = = , тогда AC= BC = BH 5) B H = 90 — BH= ABC => B H = ABC (по катету и острому углу) 6) B =AB => A B= BA= 45

10. Задача. На катетах прямоугольного треугольника, как на диаметрах, построены окружности. Найдите их общую хорду, если катеты равны 3 и 4. Решение. Пусть СD – общая хорда окружностей, построенных на катетах АС = 3 и ВС = 4 прямоугольного треугольника АВС как на диаметрах. (как вписанные углы, опирающиеся на диаметр). Значит, точка D лежит на гипотенузе АВ, а СВ – высота прямоугольного треугольника АВС, проведённая из вершины прямого угла. Тогда по теореме Пифагора: SABC= ½*AC*BC и SABC= ½*AB*CD Получаем ½*AC*BC= ½*AB*CD, откуда выражаем CD. Ответ: 2,4 А B C D

11. Задача. Найдите радиусы вписанной и описанной окружности треугольника со сторонами 13, 13, 24 и расстояние между центрами этих окружностей. Решение. Пусть CD – высота равнобедренного треугольника ABC со сторонами AC=BC=13 и AB=24, О – центр его описанной окружности радиуса R, Q – центр вписанной окружности радиуса r. Из прямоугольного треугольника ACD находим, что По теореме синусов:

Радиус окружности, вписанной в треугольник, равен площади треугольника, делённой на его полупериметр, поэтому Заметим, что поэтому точки O и Q лежат по разные стороны от AB. Следовательно OQ=OC – CQ=OC – (CD – QD)= R – (CD – r)=16,9 – (5 – 2,4)=14,3 Ответ:16,9; 2,4; 14,3.

Пропорциональные отрезки в окружности Теорема. Произведения отрезков пересекающихся хорд окружности равны, т.е. если хорды AB и CD окружности пересекаются в точке M, то AM*MB=CM*MD. Пример 1. Из точки А, лежащей вне окружности, проведены к окружности касательная и секущая. Расстояние от точки А до точки касания равно 16, а до одной из точек пересечения секущей с окружностью равно 32. Найдите радиус окружности, если расстояние от неё до центра секущей равно 5. Решение. Пусть секущая пересекает окружность в точках B и C, а М – точка касания. Тогда АМ=16, АС=32, АВ+ВС=32. По теореме о касательной и секущей AM=AC*AB, или 16²=32(32-ВС). Отсюда находим, что ВС=24. Пусть К – проекция центра О данной окружности на хорду ВС. Радиус окружности находим по теореме Пифагора из прямоугольного треугольника ОКВ: Ответ: 13

Рассмотрим ещё один пример. Пример 2. Докажите, что прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним Доказательство. Пусть А и В – точки пересечения двух окружностей, МN – общая касательная (М и N точки касания), К – точка пересечения прямых АВ и MN (А между К и В). Тогда МК²=КВ*КА и NK²=KB*KA. Следовательно МК=NK, что и требовалось доказать.

12. Задача. На продолжении диаметра АВ окружности отложен отрезок ВС, равный диаметру. Прямая, проходящая через точку С, касается окружности в точке М. Найдите площадь треугольника АСМ, если радиус окружности равен R. Решение. Пусть О – центр окружности. Тогда ОМ⏊СМ. В прямоугольном треугольнике ОМС известно, что ОМ=R и ОС=ОВ+ВС=R+2R=3R. Тогда Следовательно, Ответ:

13. Задача. Окружность S1 проходит через центр окружности S2 и пересекает её в точках A и B. Хорда AC окружности S1 касается окружности S2 в точке А и делит первую окружность на дуги, градусные меры которых относятся как 5:7. Найдите градусные меры дуг, на которые окружность S2 делится окружностью S1. Решение. Пусть О1 и О2 – центры окружностей S1 и S2 соответственно. Тогда Поскольку ∠О₁AC=90ᵒ (радиус, проведённый в точку касания, перпендикулярен касательной), отрезок О₂С – диаметр окружности S₁, поэтому Тогда градусная мера дуги окружности S₂, заключённой между сторонами угла AO₂C, равна 75ᵒ, а градусная мера дуги AB окружности S₂, содержащейся внутри окружности S₁, равна 150ᵒ. Следовательно, дополнительная к ней дуга окружности S₂ равна 360ᵒ-150ᵒ=210ᵒ Ответ: 150ᵒ, 210ᵒ

14. Задача. На стороне АВ треугольника АВС отмечена точка D, причём ∠BCD=∠BAC. Известно, что ВС=a, AC=b, AB=c. Найдите CD. Решение. Треугольники CBD и АВС подобны по двум углам, т.к. ∠BCD=∠BAC по условию, а угол при вершине В – общий. Значит, соответствующее стороны этих треугольников пропорциональны, т.е. Следовательно, Ответ:

15. Задача. Углы при вершинах A и С треугольника АВС равны 45ᵒ и 60ᵒ соответственно; АМ, BN иCK – высоты треугольника. Найдите отношение MN к KN Решение. Из прямоугольных треугольников BNC и АМС находим что CN=BCcos60ᵒ=0,5BC, CM=AC*cos60ᵒ=0,5AC, поэтому Значит, треугольник CMN подобен треугольнику САВ по двум сторонам и углу между ними (угол С – общий), причём коэффициент подобия равен Следовательно, MN=0,5AB. Аналогично получим, что треугольник AKN подобен треугольнику ACB, причём коэффициент подобия равен Значит, По теореме синусов: Следовательно: Ответ:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 966 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 688 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Гильц Светлана ИвановнаНаписать 2999 26.11.2017

Номер материала: ДБ-904031

26.11.2017 275

26.11.2017 3596

26.11.2017 3310

26.11.2017 2130

26.11.2017 1924

26.11.2017 5149

26.11.2017 235

26.11.2017 722

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔍 Видео

Геометрия Диагонали четырехугольника ABCD пересекаются в точке O Известно что угол A = углу D AO=ODСкачать

Геометрия В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8Скачать

78 Углы и диагонали четырёхугольника (146)Скачать

ОГЭ Задание 26 Теорема косинусовСкачать

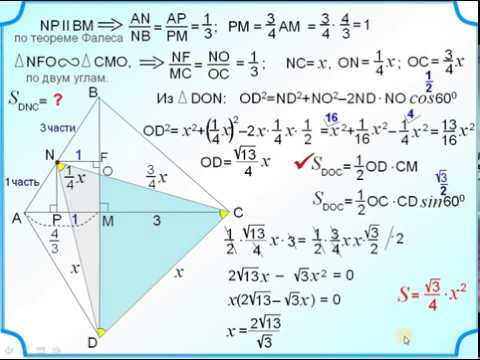
Планиметрия_03_02Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Геометрия Диагонали выпуклого четырехугольника равны 8 см и 12 см а угол между ними 30 НайдитеСкачать

✓ Площадь через диагонали | Ботай со мной #122 | Борис ТрушинСкачать

8 класс, 4 урок, ПараллелограммСкачать

Геометрия Найдите площадь выпуклого четырехугольника диагонали которого равны 3√3 см и 4 см а уголСкачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Площадь четырёхугольника через диагоналиСкачать

ОГЭ без рекламы математика 11 и 12 вариант задача 25Скачать