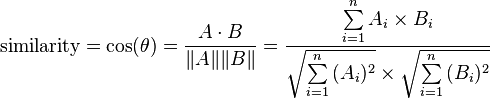Косинусное расстояние между векторами (7 видео)

Важность дистанционных метрик в моделировании машинного обучения

Дата публикации Jan 13, 2019

Ряд алгоритмов машинного обучения — контролируемых или неконтролируемых — используют метрики расстояния, чтобы знать шаблон входных данных для принятия любого решения на основе данных. Хороший показатель расстояния помогает значительно повысить производительность процессов классификации, кластеризации и поиска информации. В этой статье мы обсудим различные метрики расстояния и то, как они помогают в моделировании машинного обучения.

Содержание

Введение
Функция расстояния
Метрики расстояния
Минковский Расстояние:
Расстояние косинуса:
Махаланобис Расстояние:
Моделирование машинного обучения и дистанционные метрики
1. Классификация
2. Кластеризация
3. Обработка естественного языка
Вывод
Коллаборативная фильтрация
Косинусное расстояние как векторная функция расстояния для k-средних
3 ответов
💡 Видео

Видео:Косинусное сходство (расстояние) в Python. Cosine Similarity in Python. #python , #pythoncodeСкачать

Введение

Во многих реальных приложениях мы используем алгоритмы машинного обучения для классификации или распознавания изображений, а также для извлечения информации из содержимого изображения. Например, распознавание лиц, цензурированные изображения в Интернете, розничный каталог, системы рекомендаций и т. Д. Здесь очень важно выбрать хороший показатель расстояния. Метрика расстояния помогает алгоритмам распознавать сходства между содержимым.

Определение базовой математики (Источник Википедия),

Метрика расстояния использует функцию расстояния, которая обеспечивает метрику отношения между каждым элементом в наборе данных.

Некоторые из вас могут подумать, что это за функция расстояния? как это работает? как он решает, что определенный контент или элемент данных имеет какие-либо отношения с другим? Что ж, давайте попробуем выяснить это в следующих нескольких разделах.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Функция расстояния

Вы помните изучение теоремы Пифагора? Если вы это сделаете, то вы можете вспомнить вычисление расстояния между двумя точками данных, используя теорему.

Чтобы вычислить расстояние между точками данных A и B, в теореме Пифагора рассматривается длина осей x и y.

Многим из вас должно быть интересно, используем ли мы эту теорему в алгоритме машинного обучения, чтобы найти расстояние? Чтобы ответить на ваш вопрос, да, мы используем его. Во многих алгоритмах машинного обучения мы используем приведенную выше формулу в качестве функции расстояния. Мы поговорим об алгоритмах, где он используется.

Теперь вы, наверное, поняли, что такое функция расстояния? Вот упрощенное определение.

Основное определение от Math.net,

Функция расстояния обеспечивает расстояние между элементами набора. Если расстояние равно нулю, то элементы эквивалентны, иначе они отличаются друг от друга.

Функция расстояния — это не что иное, как математическая формула, используемая метриками расстояния. Функция расстояния может отличаться в зависимости от метрики расстояния. Давайте поговорим о различных дистанционных метриках и поймем их роль в моделировании машинного обучения.

Видео:Семинар 3 - Косинусное расстояние и близостьСкачать

Метрики расстояния

Существует несколько метрик расстояния, но для краткости этой статьи мы обсудим лишь несколько широко используемых метрик расстояния. Сначала мы попытаемся понять математику, стоящую за этими метриками, а затем определим алгоритмы машинного обучения, в которых мы используем эти метрики расстояния.

Ниже приведены часто используемые метрики расстояния —

Видео:Угол между векторами. 9 класс.Скачать

Минковский Расстояние:

Расстояние Минковского является метрикой в нормированном векторном пространстве. Что такое нормированное векторное пространство? Нормированное векторное пространство — это векторное пространство, в котором определена норма. Предположим, что X — векторное пространство, тогда норма на X — вещественная функция ||Икс|| который удовлетворяет условиям ниже —

Нулевой вектор-Нулевой вектор будет иметь нулевую длину.
Скалярный фактор-Направление вектора не меняется, когда вы умножаете его на положительное число, хотя его длина будет изменена.
Неравенство треугольникаЕсли расстояние является нормой, то рассчитанное расстояние между двумя точками всегда будет прямой линией.

Вам может быть интересно, зачем нам нужен нормированный вектор, не можем ли мы просто перейти к простым метрикам? Поскольку нормированный вектор обладает указанными выше свойствами, это помогает поддерживать индуцированную норму метрико-однородной и трансляционной инвариантом. Более подробную информацию можно найтиВот,

Расстояние можно рассчитать по приведенной ниже формуле —

Расстояние Минковского является обобщенной метрикой расстояния. Здесь обобщенный означает, что мы можем манипулировать приведенной выше формулой, чтобы рассчитать расстояние между двумя точками данных различными способами.

Как уже упоминалось выше, мы можем манипулировать значениемпи рассчитать расстояние тремя разными способами-

р = 2, евклидово расстояние

р = ∞, расстояние чебычева

Мы обсудим эти метрики расстояния ниже подробно.

Манхэттен Расстояние:

Мы используем Манхэттенское расстояние, если нам нужно рассчитать расстояние между двумя точками данных в виде сетки, как путь. Как уже упоминалось выше, мы используемМинковское расстояниеформула, чтобы найти расстояние Манхэттена, установивр-хзначение как1,

Допустим, мы хотим рассчитать расстояние,dмежду двумя точками данныхИкса такжеY

Расстояниеdбудет рассчитываться с использованиемабсолютная сумма разностеймежду его декартовыми координатами, как показано ниже:

где, n- количество переменных,XIа такжеугявляются переменными векторов x и y соответственно в двумерном векторном пространстве. то естьх = (х1, х2, х3, . )а такжеу = (у1, у2, у3,…),

Теперь расстояниеdбудет рассчитываться как

(x1 — y1)+(x2 — y2)+(х3 — у3)+… +(xn — yn),

Если вы попытаетесь визуализировать расчет расстояния, он будет выглядеть примерно так:

Расстояние до Манхэттена также известно как геометрия такси, расстояние до городских кварталов и т.д.

Евклидово расстояние:

Евклидово расстояние — одна из наиболее часто используемых метрик расстояния. Он рассчитывается по формуле Минковского расстояния путем установкир-хзначение для2, Это обновит расстояние«D»формула как ниже:

Давай остановимся ненадолго! Эта формула выглядит знакомо? Ну да, мы только что видели эту формулу выше в этой статье при обсуждении«Теорема Пифагора».

Евклидова формула расстояния может быть использована для расчета расстояния между двумя точками данных на плоскости.

Видео:Угол между векторами | МатематикаСкачать

Расстояние косинуса:

В основном, метрика косинусного расстояния используется для поиска сходства между различными документами. В косинусной метрике мы измеряем степень угла между двумя документами / векторами (термин частоты в разных документах собирается как метрика). Эта конкретная метрика используется, когда величина между векторами не имеет значения, но ориентация.

Формула подобия косинуса может быть получена из уравнения точечных произведений:

Теперь вы должны подумать, какое значение угла косинуса будет полезно для определения сходства.

Теперь, когда у нас есть значения, которые будут рассматриваться для измерения сходства, нам нужно знать, что означают 1, 0 и -1.

Здесь значение косинуса 1 предназначено для векторов, указывающих в одном и том же направлении, то есть между документами / точками данных есть сходства. В нуле для ортогональных векторов, т. Е. Не связанных (найдено некоторое сходство). Значение -1 для векторов, указывающих в противоположных направлениях (без сходства).

Видео:косинусное расстояниеСкачать

Махаланобис Расстояние:

Расстояние Махаланобиса используется для расчета расстояния между двумя точками данных в многомерном пространстве.

Согласно определению Википедии,

Махаланобис расстояниеявляется мерой расстояния между точкой P и распределением D. Идея измерения состоит в том, сколько стандартных отклонений P от среднего значения D.

Преимущество использования расстояния по махаланобису заключается в том, что учитывается ковариация, которая помогает измерять силу / сходство между двумя различными объектами данных. Расстояние между наблюдением и средним может быть рассчитано, как показано ниже:

Здесь S — ковариационные метрики. Мы используем обратную метрику ковариации, чтобы получить нормализованное по дисперсии уравнение расстояния.

Теперь, когда у нас есть базовое представление о различных метриках расстояния, мы можем перейти к следующему шагу, а именно к методам / моделированию машинного обучения, в которых используются эти метрики различий.

Видео:Косинус угла между векторами. Коллинеарность векторовСкачать

Моделирование машинного обучения и дистанционные метрики

В этом разделе мы будем работать над некоторыми базовыми вариантами использования для классификации и кластеризации. Это поможет нам понять использование метрик расстояния в моделировании машинного обучения. Мы начнем с быстрого введения контролируемых и неконтролируемых алгоритмов и постепенно перейдем к примерам.

Видео:Как находить угол между векторамиСкачать

1. Классификация

K-Ближайшие соседи (KNN) —

KNN — это не вероятностный контролируемый алгоритм обучения, т.е. он не дает вероятности принадлежности к какой-либо точке данных, а KNN классифицирует данные при жестком назначении, например, точка данных будет принадлежать 0 или 1. Теперь вы должны подумать как работает KNN, если не используется уравнение вероятности. KNN использует метрики расстояния, чтобы найти сходства или различия.

Давайте возьмем набор данных iris, который имеет три класса, и посмотрим, как KNN будет определять классы для тестовых данных.

На изображении № 2 над черным квадратом находится тестовая точка данных. Теперь нам нужно найти, к какому классу относится эта контрольная точка данных, с помощью алгоритма KNN. Теперь мы подготовим набор данных для создания модели машинного обучения, чтобы предсказать класс для наших тестовых данных.

В алгоритме классификации КНН мы определяем постоянную«K».K — количество ближайших соседей контрольной точки данных. Эти K точек данных затем будут использоваться для определения класса для точки тестовых данных (обратите внимание, что это в наборе обучающих данных).

Вам интересно, как бы мы нашли ближайших соседей. Ну вот где метрика расстояния входит в картинки. Сначала мы рассчитываем расстояние между каждым поездом и контрольной точкой данных, а затем выбираем ближайшую вершину в соответствии со значением k.

Мы не будем создавать KNN с нуля, но будем использовать scikit KNN классификатор

Как видно из приведенного выше кода, мы используем метрику расстояния Минковского со значением p, равным 2, то есть в классификаторе KNN будет использоваться формула Евклидовой метрики расстояния.

По мере продвижения вперед в моделировании машинного обучения мы можем теперь обучать нашу модель и начинать предсказывать класс для тестовых данных.

Как только верхние ближайшие соседи выбраны, мы проверяем большинство проголосовавших классов в соседях —

Из приведенного выше изображения, вы можете угадать класс для контрольной точки? Это класс 1, так как он является самым популярным.

Из этого небольшого примера мы увидели, какметрика расстояниябыл важен для классификатора KNN.Это помогло нам получить самые близкие точки данных поезда, для которых были известны классы.Существует вероятность, что при использовании различных метрик расстояния мы могли бы получить лучшие результаты. Таким образом, в не вероятностном алгоритме, таком как KNN, метрики расстояния играют важную роль.

Видео:А.5.9 Евклидово расстояние между точками (длина отрезка)Скачать

2. Кластеризация

K-нуждаемость

В алгоритмах классификации, вероятностных или не вероятностных, нам будут предоставлены помеченные данные, что упрощает прогнозирование классов. Хотя в алгоритме кластеризации у нас нет информации о том, какая точка данных принадлежит какому классу. Метрики расстояния являются важной частью этого вида алгоритма.

В K-средних мы выбираем количество центроидов, которые определяют количество кластеров.Затем каждая точка данных будет привязана к ближайшему центроиду, используя метрику расстояния (евклидово), Мы будем использовать данные радужной оболочки, чтобы понять основной процесс K-средних.

На приведенном выше изображении № 1, как вы можете видеть, мы случайно разместили центроиды, а на рисунке № 2, используя метрику расстояния, пытались найти ближайший класс кластеров.

Нам нужно будет повторять назначение центроидов до тех пор, пока у нас не будет четкой кластерной структуры.

Как мы видели в приведенном выше примере, не имея никаких знаний о метках с помощью метрики расстояния в K-средних, мы разбили данные на 3 класса.

Видео:Линейная алгебра в Python: точечное произведение векторов, корреляция Пирсона, косинусное расстояниеСкачать

3. Обработка естественного языка

Поиск информации

В поиске информации мы работаем с неструктурированными данными. Данные могут быть статьей, веб-сайтом, электронной почтой, текстовыми сообщениями, публикацией в социальных сетях и т. Д. С помощью методов, используемых в НЛП, мы можем создавать векторные данные таким образом, чтобы их можно было использовать для получения информации при запросе. Как только неструктурированные данные преобразуются в векторную форму, мы можем использовать метрику косинусного сходства, чтобы отфильтровать ненужные документы из корпуса.

Давайте возьмем пример и поймем использование косинусного сходства.

Создать векторную форму для Корпуса и Query-

2. Проверьте сходства, т.е. найдите, какой документ в корпусе имеет отношение к нашему запросу.

Как видно из приведенного выше примера, мы запросили слово«Коричневый»и в корпусе есть только три документа, которые содержат слово«Коричневый».При проверке с помощью косинусной метрики сходства он дал те же результаты, имея> 0 значений для трех документов, кроме четвертого

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Вывод

В этой статье мы узнали о нескольких популярных метриках расстояния / сходства и о том, как их можно использовать для решения сложных задач машинного обучения. Надеюсь, что это будет полезно для людей, которые только начинают изучать машинное обучение и науку о данных.

Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Коллаборативная фильтрация

В современном мире часто приходится сталкиваться с проблемой рекомендации товаров или услуг пользователям какой-либо информационной системы. В старые времена для формирования рекомендаций обходились сводкой наиболее популярных продуктов: это можно наблюдать и сейчас, открыв тот же Google Play. Но со временем такие рекомендации стали вытесняться таргетированными (целевыми) предложениями: пользователям рекомендуются не просто популярные продукты, а те продукты, которые наверняка понравятся именно им. Не так давно компания Netflix проводила конкурс с призовым фондом в 1 миллион долларов, задачей которого стояло улучшение алгоритма рекомендации фильмов (подробнее). Как же работают подобные алгоритмы?

В данной статье рассматривается алгоритм коллаборативной фильтрации по схожести пользователей, определяемой с использованием косинусной меры, а также его реализация на python.

Входные данные

Допустим, у нас имеется матрица оценок, выставленных пользователями продуктам, для простоты изложения продуктам присвоены номера 1-9:

Задать её можно при помощи csv-файла, в котором первым столбцом будет имя пользователя, вторым — идентификатор продукта, третьим — выставленная пользователем оценка. Таким образом, нам нужен csv-файл со следующим содержимым:

Для начала разработаем функцию, которая прочитает приведенный выше csv-файл. Для хранения рекомендаций будем использовать стандартную для python структуру данных dict: каждому пользователю ставится в соответствие справочник его оценок вида «продукт»:«оценка». Получится следующий код:

Мера схожести

Интуитивно понятно, что для рекомендации пользователю №1 какого-либо продукта, выбирать нужно из продуктов, которые нравятся каким-то пользователям 2-3-4-etc., которые наиболее похожи по своим оценкам на пользователя №1. Как же получить численное выражение этой «похожести» пользователей? Допустим, у нас есть M продуктов. Оценки, выставленные отдельно взятым пользователем, представляют собой вектор в M-мерном пространстве продуктов, а сравнивать вектора мы умеем. Среди возможных мер можно выделить следующие:

Косинусная мера
Коэффициент корреляции Пирсона
Евклидово расстояние
Коэффициент Танимото
Манхэттенское расстояние и т.д.

Более подробно различные меры и аспекты их применения я собираюсь рассмотреть в отдельной статье. Пока же достаточно сказать, что в рекомендательных системах наиболее часто используются косинусная мера и коэффициент корреляции Танимото. Рассмотрим более подробно косинусную меру, которую мы и собираемся реализовать. Косинусная мера для двух векторов — это косинус угла между ними. Из школьного курса математики мы помним, что косинус угла между двумя векторами — это их скалярное произведение, деленное на длину каждого из двух векторов:

Реализуем вычисление этой меры, не забывая о том, что у нас множество оценок пользователя представлено в виде dict «продукт»:«оценка»

При реализации был использован факт, что скалярное произведение вектора самого на себя дает квадрат длины вектора — это не лучшее решение с точки зрения производительности, но в нашем примере скорость работы не принципиальна.

Алгоритм коллаборативной фильтрации

Итак, у нас есть матрица предпочтений пользователей и мы умеем определять, насколько два пользователя похожи друг на друга. Теперь осталось реализовать алгоритм коллаборативной фильтрации, который состоит в следующем:

Выбрать L пользователей, вкусы которых больше всего похожи на вкусы рассматриваемого. Для этого для каждого из пользователей нужно вычислить выбранную меру (в нашем случае косинусную) в отношении рассматриваемого пользователя, и выбрать L наибольших. Для Ивана из таблицы, приведенной выше, мы получим следующие значения:
Для каждого из пользователей умножить его оценки на вычисленную величину меры, таким образом оценки более «похожих» пользователей будут сильнее влиять на итоговую позицию продукта, что можно увидеть в таблице на иллюстрации ниже
Для каждого из продуктов посчитать сумму калиброванных оценок L наиболее близких пользователей, полученную сумму разделить на сумму мер L выбранных пользователей. Сумма представлена на иллюстрации в строке «sum», итоговое значение в строке «result»

Серым цветом отмечены столбцы продуктов, которые уже были оценены рассматриваемым пользователем и повторно предлагать их ему не имеет смысла

В виде формулы этот алгоритм может быть представлен как

где функция sim — выбранная нами мера схожести двух пользователей, U — множество пользователей, r — выставленная оценка, k — нормировочный коэффициент:

Теперь осталось только написать соответствующий код

Для проверки его работоспособности можно выполнить следующую команду:

Что приведет к следующему результату:

Видео:Успешное собеседование в Яндекс | Секция Machine LearningСкачать

Косинусное расстояние как векторная функция расстояния для k-средних

у меня есть граф из N вершин, где каждая вершина представляет место. Также у меня есть векторы, по одному на пользователя, каждый из N коэффициентов, где значение коэффициента-продолжительность в секундах, проведенных в соответствующем месте или 0, если это место не было посещено.

означало бы, что мы потратили:

(вершины 3 & 5, где не побывал, таким образом, 0С).

Я хочу запустить кластеризацию k-means, и я выбрал cosine_distance = 1 — cosine_similarity как метрика для расстояний, где формула для cosine_similarity — это:

как рассказали здесь.

но я заметил следующее. Предположим k=2 и один из векторов является:

в процессе решения оптимизационной задачи минимизации общего расстояния от центроидов-кандидатов предположим, что в какой-то момент, 2 центроиды-кандидаты:

под управлением cosine_distance формула для (v1, c1) и (v1, c2) мы получаем точно такое же расстояние 0.5527864045 для обоих.

Я бы предположил, что v1 больше похож (ближе) на c1, чем c2. Очевидно, это не так.

Q1. Почему это предположение неверно?

Q2. Является ли косинусное расстояние правильной функцией расстояния для этого случая?

Q3. Что было бы лучше, учитывая природу проблема?

Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

3 ответов

давайте разделим косинусное сходство на части и посмотрим как и почему это работает.

косинус угла между 2 векторами — a и b — определяется как:

здесь .* является умножением по элементам. Знаменатель здесь только для нормализации, поэтому давайте просто назовем его L . С ним наши функции превращаются в:

, который, в свою очередь, может быть переписан как:

давайте немного абстрактнее и заменим x * y / L С функцией g(x, y) ( L здесь константа, поэтому мы не ставим ее в качестве аргумента функции). Таким образом, наша косинусная функция становится:

то есть, каждая пара элементов (a[i], b[i]) is отдельно, и результат просто sum всех процедур. И это хорошо для вашего случая, потому что вы не хотите, чтобы разные пары (разные вершины) возились с каждым другое: если user1 посетил только vertex2 и user2 — только vertex1, то у них нет ничего общего, и сходство между ними должно быть нулевым. Что вам на самом деле не нравится, так это то, как сходство между отдельными парами — т. е. функция g() — рассчитывается.

С косинусной функцией сходство между отдельными парами выглядит так:

здесь x и y представляют время, затраченное пользователями на вершину. И вот главный вопрос:—44—>тут умножение представляет сходство между отдельными парами хорошо? Я так не думаю. Пользователь, который провел 90 секунд на какой-то вершине, должен быть близок к пользователю, который провел там, скажем, 70 или 110 секунд, но гораздо дальше от пользователей, которые проводят там 1000 или 0 секунд. Умножение (даже нормализованное на L ) здесь полностью вводит в заблуждение. Что значит умножить 2 периода времени?

хорошая новость заключается в том, что это вы, кто проектирует функцию подобия. Мы уже решили, что удовлетворены независимой обработкой пар (вершин), и нам нужна только индивидуальная функция подобия g(x, y) чтобы сделать что-то разумное с ее доводами. И что такое разумная функция для сравнения периодов времени? Я бы сказал, что вычитание-хороший кандидат:

это не функция подобия, а функция расстояния-чем ближе значения друг к другу, тем меньше результат g() — но в конечном итоге идея одна и та же, поэтому мы можем обмениваться ими когда понадобится.

мы также можем захотеть увеличить влияние больших несоответствий путем возведения разницы в квадрат:

Эй! Мы только что изобрели (среднее) квадратов ошибок! Теперь мы можем придерживаться MSE для расчета расстояния, или мы можем продолжить поиск хорошего

косинусное сходство предназначено для случая, когда вы делаете не хотите взять длину в accoun,но только угол. Если вы хотите также включить длину, выберите другую функцию расстояния.

Косинус расстояние is тесно связано с квадратным евклидовым расстоянием (единственное расстояние, для которого действительно определено k-среднее); поэтому сферическое k-среднее работает.

связь довольно проста:

квадрат евклидова расстояния sum_i (x_i-y_i)^2 можно учесть в sum_i x_i^2 + sum_i y_i^2 — 2 * sum_i x_i*y_i . Если оба вектора нормализованы, т. е. длина не имеет значения, то первые два условия 1. В этом случае, квадрат евклидова расстояния равен 2 — 2 * cos(x,y) !

другими словами: расстояние Косинуса в квадрате евклидово расстояние с данными, нормализованными к единичной длине.

Если вы не хотите нормализовать свои данные, не используйте Косинус.

Q1. Why is this assumption wrong?

как мы видим из определения, косинусное сходство измеряет угол между 2 векторами.

в вашем случае, вектор v1 лежит плашмя на первом измерении, в то время как c1 и c2 оба одинаково выровнены по осям, и, таким образом, косинусное сходство и чтобы быть таким же.

обратите внимание, что проблема заключается в c1 и c2 указывая в том же направлении. любой v1 будет иметь тот же Косинус сходство с ними обоими. Для примера :