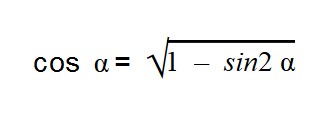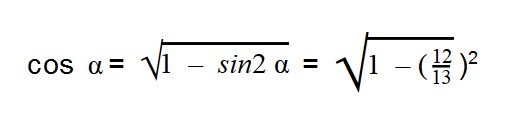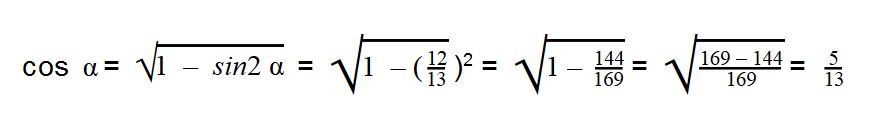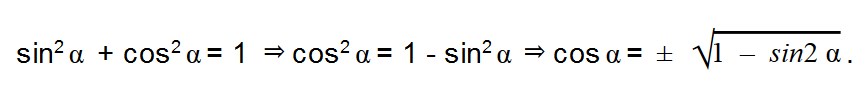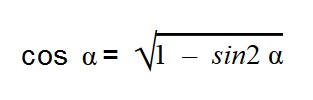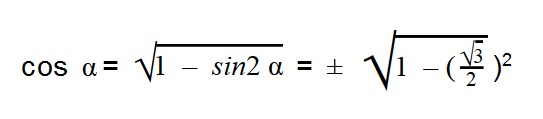| 1. Определение тригонометрических функций | ||
| Через единичную окружность (R = 1) | Через произвольную окружность (R — радиус окружности) | Через прямоугольный треугольник (для острых углов) |
| tg α = y/x = sin α / cos α |
| ctg α = x/y = cos α / sin α |
sin (числа α) = sin (угла в α радиан)
cos (числа α) = cos (угла в α радиан)
tg (числа α) = tg (угла в α радиан)
ctg (числа α) = ctg (угла в α радиан)
| * Это следует из того, что две концентрические окружности гомотетичны (центр гомотетии — точка О, а коэффициент гомотетии k — отношение радиусов этих окружностей), тогда и точки Pα на этих окружностях также будут гомотетичны. Таким образом, при переходе от одной окружности к другой в определениях тригонометрических функций числитель и знаменатель соответствующей дроби умножаются на k, а значение дроби не изменяется. |
Окружность радиуса 1 с центром в начале координат будем называть единичной окружностью.
Пусть при повороте на угол α точка P0 (1; 0) переходит в точку Pα (x; y)
(то есть при повороте на угол α радиус OP0 переходит в радиус OPα) (рис. 63).
Синусом угла α называется ордината точки Pα (x; y) единичной окружности:
Косинусом угла α называется абсцисса точки Pα (x; y) единичной окружности:
Тангенсом угла α называется отношение ординаты точки Pα (x; y) единичной окружности к ее абсциссе, то есть отношение sin α / cos α.
 |  |
Таким образом, tg α = sin α / cos α (где cos α ≠ 0).
Заметим, что при cos α = 0 значение функции tg α не определено, а значение функции ctg α не определено при sin α = 0.
| Пример |
Пользуясь этими определениями, найдем синус, косинус, тангенс и котангенс угла 2π / 3 радиан.
♦ Рассмотрим единичную окружность (рис. 64). При повороте на угол 2π / 3 радиус OP0 переходит в радиус OP2π/3 (а точка P0 переходит в точку P2π/3). Координаты точки P2π/3 можно найти, используя свойства прямоугольного треугольника OAP2π/3 (с углами 60° и 30° и гипотенузой 1): x = — OA=−1/2; y = AP2π/3 = √3/2. Тогда: sin 2π/3 = y = √3/2; cos 2π/3 = x = -1/2; tg 2π/3 = sin 2π/3 / cos 2π/3 = — √3; ctg 2π/3 = — 1/√3.◊
Аналогично находятся значения синуса, косинуса, тангенса и котангенса углов, градусные и радианные меры которых указаны в верхней строке таблицы 19 (с. 156).
Укажем, что таким образом можно найти тригонометрические функции только некоторых углов. Тригонометрические функции произвольного угла обычно находят с помощью калькулятора или таблиц.
2. Тригонометрические функции числового аргумента. Введенные определения позволяют рассматривать не только тригонометрические функции углов, но и тригонометрические функции числовых аргументов, если рассматривать тригонометрические функции числа α как соответствующие тригонометрические функции угла в α радиан. То есть:
синус числа α — это синус угла в α радиан;
косинус числа α — это косинус угла в α радиан.
Например: sin π/6 = sin (π/6 радиан) = sin 30° = 1/2 (см. также пункт 2 табл. 7).
| α | градусы | 0 º | 30 º | 45 º | 60 º | 90 º | 180 º | 270 º | 360 º |
| радианы | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 | |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 | |
| tg α | 0 | √3/3 | 1 | √3 | — | 0 | — | 0 | |
| ctg α | — | √3 | 1 | √3/3 | 0 | — | 0 | — | |
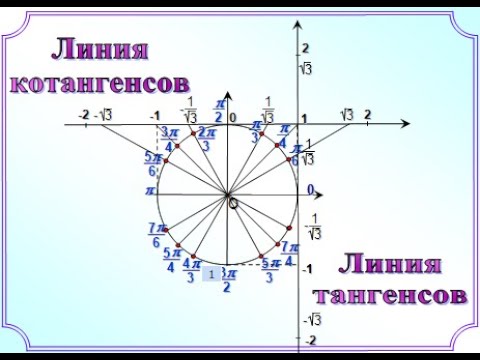
3. Линии тангенсов и котангенсов. Для решения некоторых задач полезно иметь представление о линиях тангенсов и котангенсов.
♦ Проведем через точку P0 единичной окружности прямую AP0, параллельную оси Oy (рис. 65). Эта прямая называется линией тангенсов.
Пусть α — произвольное число (или угол), для которого cos α ≠ 0. Тогда точка Pα не лежит на оси Oy и прямая OPα пересекает линию тангенсов в точке A. Поскольку прямая OPα проходит через начало координат, то ее уравнение имеет вид y = kx. Но эта прямая проходит через точку Pα с координатами (cos α; sin α), значит, координаты точки Pα удовлетворяют уравнению прямой y = kx, то есть sin α = k cos α. Отсюда k = sin α / cos α = tg α. Следовательно, прямая OPα имеет уравнение
y = (tg α) x. Прямая AP0 имеет уравнение x = 1. Чтобы найти ординату точки A, достаточно в уравнение прямой OPα подставить x = 1. Получаем yA = tg α. Таким образом,
тангенс угла (числа) α — это ордината соответствующей точки на линии тангенсов.◊
Аналогично вводится и понятие линии котангенсов: это прямая CB (рис. 66), которая проходит через точку C (0; 1) единичной окружности параллельно оси Ox.
Если α — произвольное число (или угол), для которого sin α ≠ 0 (то есть точка Pα не лежит на оси Ox), то прямая OPα пересекает линию котангенсов в некоторой точке B (xB; 1).
Аналогично вышеизложенному обосновывается, что xB = ctg α, таким образом,
котангенс угла (числа) α — это абсцисса соответствующей точки на линии котангенсов.
Вопросы для контроля
1. Сформулируйте определения тригонометрических функций острого угла в прямоугольном треугольнике.
2. Сформулируйте определения тригонометрических функций произвольного угла:
а) используя окружность радиуса R с центром в начале координат;
б) используя единичную окружность.
3. Что имеют в виду, когда говорят о синусе, косинусе, тангенсе и котангенсе числа α?
Упражнения
1°. Постройте на единичной окружности точку Pα, в которую переходит точка P0 (1; 0) единичной окружности при повороте на угол α. В какой координатной четверти находится точка Pα в заданиях 3–6?
1) α = 3π; 2) α = –4π; 3) α=7π/6;
4) α=−3π/4; 5) α=4π/3; 6) α=7π/4.
2. Найдите значение sin α, cos α, tg α, ctg α (если они существуют) при:
1) α = 3π; 2) α = –4π; 3) α=−π/2;
4) α=5π/2; 5*) α=−5π/6; 6*) α=3π/4.
3°. Пользуясь определением синуса и косинуса, с помощью единичной окружности укажите знаки sin α и cos α, если:
1) α=6π/5; 2) α=−π/6; 3) α=5π/6;
4*. Пользуясь линией тангенсов, укажите знак tg α, если:
1) α=4π/3; 2) α=−3π/4; 3) α=11π/6;
5*. Пользуясь линией котангенсов, укажите знак сtg α, если:
1) α=−4π/3; 2) α=3π/4; 3) α=−11π/6;
- Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
- Синус, косинус, тангенс и котангенс. Определения
- Угол поворота
- Числа
- Тригонометрические функции углового и числового аргумента
- Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
- Основное тригонометрическое тождество
- Связь между sin и cos одного угла
- Тангенс и котангенс через синус и косинус
- Связь между тангенсом и котангенсом
- Тангенс и косинус, котангенс и синус
- Примеры решения задач
- 💥 Видео
Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Видео:Тригонометрическая окружность. Как выучить?Скачать

Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Видео:9 класс, 9 урок, Синус, косинус, тангенс, котангенсСкачать

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Видео:Алгебра 10 класс (Урок№33 - Синус, косинус и тангенс аргументов а и -а.)Скачать

Основное тригонометрическое тождество
О чем эта статья:
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Это значит, что точка A1 получает координаты cos α, sin α.
Образовался прямоугольный треугольник OA1B.
|OB| = |x|.
Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B| 2 + |OB| 2 = |OA1| 2 .
Записываем в виде: |y| 2 + |x| 2 = 1 2 .
Это значит, что y 2 + x 2 = 1.
sin угла α = y
cos угла α = x
Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Видео:Определение синуса косинуса тангенса котангенса на единичной окружности. Шпаргалка по тригонометрииСкачать

Тангенс и котангенс через синус и косинус
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
- tg α =
=
- ctg α =
=
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
ctg α = x/y
 и
и  ,
, получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg 2 α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg 2 α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
- Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
- В результате деления получаем формулу tg 2 α + 1 =
- Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
1 + ctg 2 α =.
- Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 =
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg 2 α =
применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:
Вычисляем:
Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
Таким же образом, используя формулу, вычисляем значение котангенса:
Задачка 2. Найдите значение cos α,
если:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:

Подставляем значения sin α:
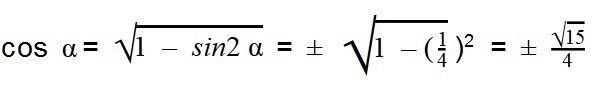
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
💥 Видео
9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

6 Линия тангенсов и линия котангенсовСкачать
Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Алгебра 10 класс (Урок№31 - Знаки синуса, косинуса и тангенса.)Скачать

Определение тангенса и котангенса на единичной окружности. Алгебра 10 класс.Скачать

Алгебра 10 класс (Урок№30 - Определение синуса, косинуса и тангенса угла.)Скачать

Алгебра 10 класс Определение синуса, косинуса, тангенса угла ЛекцияСкачать

Тангенс и котангенс произвольного угла. 9 класс.Скачать

















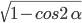
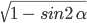
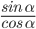
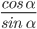
 =
= 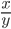 =
= 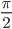 + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.