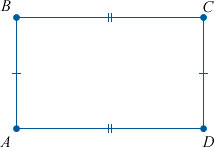
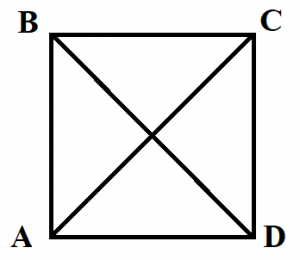
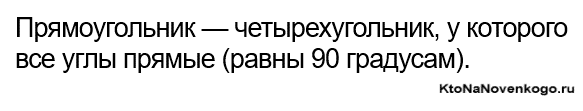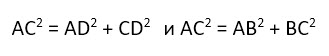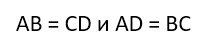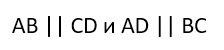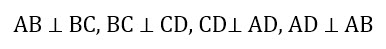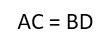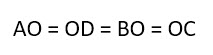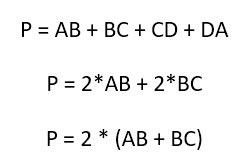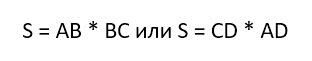Верно ли что если в четырехугольнике противоположные углы прямые то это прямоугольник нет (8 видео)

Прямоугольник

Частным видом параллелограмма является прямоугольник.

Прямоугольником называют параллелограмм, у которого все углы прямые

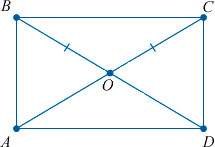
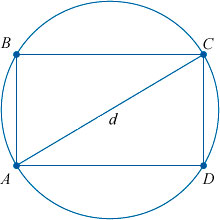
ABCD — прямоугольник.

Содержание

Особое свойство прямоугольника
Доказательство
Теорема
Доказательство
Теорема
Доказательство
Прямоугольник — это одна из основ геометрии
Прямоугольник — это.
Признаки прямоугольника
Диагонали прямоугольника
Свойства прямоугольника
Периметр и площадь
Комментарии и отзывы (5)
Четырехугольники
теория по математике 📈 планиметрия
Выпуклый четырехугольник
Виды и свойства выпуклых четырехугольников
Прямоугольник
Квадрат
Параллелограмм
Трапеция
Виды трапеций
Средняя линия трапеции
🔥 Видео

Особое свойство прямоугольника

Диагонали прямоугольника равны

Доказательство

Дано: ABCD — прямоугольник

Доказать: AC = DB

Доказательство:

Рассмотрим ABD иACB: ABCD — прямоугольник, А и B — прямые, ABD иACB — прямоугольные. AD = CB (по свойству параллелограмма). AB — общий катет, ABD =ACB (по двум катетам). А в равных треугольниках против соответственно равных углов лежат равные стороны, значит, AC = DB, что и требовалось доказать.

Теорема

Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник

Доказательство

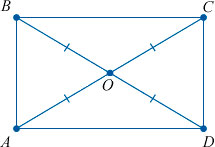
Дано: ABCD — параллелограмм, AC = DB

Доказать: ABCD — прямоугольник

Доказательство:

Рассмотрим ABD иACB:

AC = DB (по условию), AD = BC (по свойству параллелограмма), AB — общая, ABD =ACB (по трем сторонам). А в равных треугольниках против соответственно равных сторон лежат равные углы, A = B. А в параллелограмме противоположные углы равны, значит A = C и В = D, A = В = C = D (1). A + В + C + D = 360 0 (2)(т.к. параллелограмм выпуклый четырёхугольник). Следовательно, из (2), учитывая (1), получаем, что A = В = C = D = 90 0 , ABCD — прямоугольник, что и требовалось доказать.

Теорема

Если один из углов параллелограмма прямой, то этот параллелограмм — прямоугольник

Доказательство

Дано: ABCD — параллелограмм, A = 90 0

Доказать: ABCD — прямоугольник

Доказательство:

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0 , т.е. A + В = 180 0 , В = 180 0 — A = 180 0 — 90 0 = 90 0

Противолежащие углы параллелограмма равны, A = C = 90 0 и В = D = 90 0

Итак: ABCD — параллелограмм (по условию), и все его углы прямые (по доказанному выше), ABCD — прямоугольник (по определению), что и требовалось доказать.

Две теоремы, доказанные выше, называют признаками прямоугольника.

Поделись с друзьями в социальных сетях:

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Прямоугольник — это одна из основ геометрии

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.

Название это весьма говорящее, и в нем скрыто официальное определение.

Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.

Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.

Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».

Видео:№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать

Прямоугольник — это.

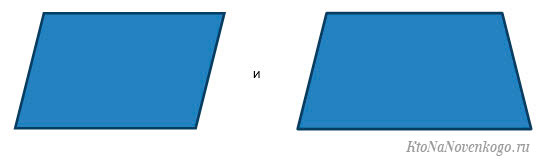
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).

У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.

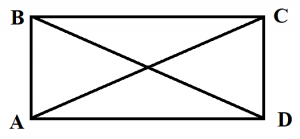
То есть выглядит это так:

Так вот, прямоугольник в данном случае является частным случаем параллелограмма.

У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.

У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.

Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.

Видео:Прямоугольник. 8 класс.Скачать

Признаки прямоугольника

Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.

В случае с прямоугольником их всего три:

Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.

» alt=»»>

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Диагонали прямоугольника

Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.

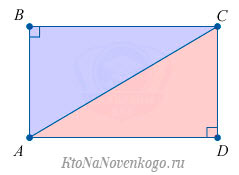
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».

В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:

Видео:Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать

Свойства прямоугольника

К свойствам прямоугольника относятся следующие утверждения:

является параллелограммом

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Периметр и площадь

Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.

Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:

Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:

К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.

Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (5)

Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.

Прямоугольник отличается от квадрата, этому учат в школе в младших классах. Квадрат — это одинаковая длина соединяющих углов, если я правильно выражаюсь, а прямоугольник формы может быть: телефон, звуковые колонки, паспорт и прочее.

Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.

Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.

Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Четырехугольники

теория по математике 📈 планиметрия

Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Определение

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Виды и свойства выпуклых четырехугольников

Сумма углов выпуклого четырехугольника равна 360 градусов.

Прямоугольник

Прямоугольник – это четырехугольник, у которого все углы прямые.

На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь

Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
Диагонали прямоугольника равны (АС=ВD).
Диагонали пересекаются и точкой пересечения делятся пополам.
Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:

S=ab, где a и b соседние стороны прямоугольника.

Квадрат

Квадрат – это прямоугольник, у которого все стороны равны.

Свойства квадрата

Диагонали квадрата равны (BD=AC).
Диагонали квадрата пересекаются под углом 90 градусов.
Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.

Параллелограмм

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция

Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций

Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов

Средняя линия трапеции

Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.

Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.

По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17

Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).

Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .

Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула

S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63

pазбирался: Даниил Романович | обсудить разбор | оценить

Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .

Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:

с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88

pазбирался: Даниил Романович | обсудить разбор | оценить

Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8

Для выполнения данного задания надо подставить все известные данные в формулу:

12,8= d 1 × 16 × 2 5 . . 2 . .

В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .

Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2

Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4

pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.

Задание №1

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.

Объекты	яблони	теплица	сарай	жилой дом
Цифры

Решение

Для решения 1 задачи работаем с текстом и планом одновременно:

при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.

Итак, получили следующее:

1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.

Заполняем нашу таблицу:

Объекты	яблони	теплица	сарай	жилой дом
Цифры	3	5	1	7

Записываем ответ: 3517

Задание №2

Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

Решение

Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».

Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.

Задание №3

Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение

Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4

Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.

Решение

Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м

Задание №5

Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.

Номер магазина	Расход краски	Масса краски в одной банке	Стоимость одной банки краски	Стоимость доставки заказа
1	0,25 кг/кв.м	6 кг	3000 руб.	500 руб.
2	0,4 кг/кв.м	5 кг	1900 руб.	800 руб.

Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?

Решение

Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:

1 магазин: 232х0,25=58 кг

2 магазин: 232х0,4=92,8 кг

Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:

1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)

2 магазин: 92,8:5=18,56; значит надо 19 банок.

Вычислим стоимость краски в каждом магазине плюс доставка:

1 магазин: 10х3000+500=30500 руб.

2 магазин: 19х1900+800=36900 руб.

Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить