Как найти половину диагонали треугольника

Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.

Видео:как найти диагональ.Скачать

Треугольник

Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:

Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.

Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует

Рис. 1. Три медианы в треугольнике.

Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Прямоугольник

Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.

Диагональ прямоугольника или квадрата всегда:

• Делит фигуру на две равных прямоугольных треугольника.
• В полученных треугольниках диагональ будет являться гипотенузой
• Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора

Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.

При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.

Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.

Видео:Теорема Пифагора для чайников)))Скачать

Многоугольник

На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.

Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

Рис. 2. Диагонали многоугольника.

В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.

Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.

Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.

Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.

Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:

$P=<n(n-3)over>$ – где n это число сторон многоугольника.

Проверим для квадрата:

Рис. 3. Диагонали квадрата.

Видео:Как найти диагональ... Диагональни топишСкачать

Что мы узнали?

Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Как найти диагонали треугольника

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Посчитать диагональ прямоугольника

Видео:Как найти площадь треугольника без формулы?Скачать

Онлайн калькулятор

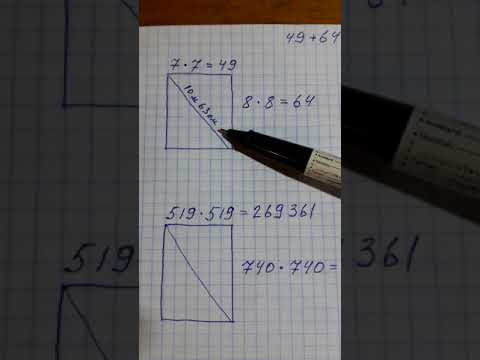
Посчитать чему равна диагональ (d) любого прямоугольника (в том числе и квадрата) можно зная длины его сторон (a и b).

Просто подставьте их в калькулятор и получите результат.

Теория

Чему равна диагональ прямоугольника d если известны длина стороны a и длина стороны b?

Формула

Пример

Если сторона a = 10 см, а сторона b = 5 см, то:

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Диагональ треугольника – формула

Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.

Видео:КАК НАЙТИ ДИАГОНАЛЬ И ВЫВЕСТИ УГЛЫ 90 ГРАДУСОВСкачать

Треугольник

Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:

Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.

Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует

Рис. 1. Три медианы в треугольнике.

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Прямоугольник

Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.

Диагональ прямоугольника или квадрата всегда:

• Делит фигуру на две равных прямоугольных треугольника.
• В полученных треугольниках диагональ будет являться гипотенузой
• Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора

Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.

При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.

Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Многоугольник

На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.

Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

Рис. 2. Диагонали многоугольника.

В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.

Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.

Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.

Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.

Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:

$P= >$ – где n это число сторон многоугольника.

Проверим для квадрата:

Рис. 3. Диагонали квадрата.

Видео:Задача: найти площадь квадрата если его диагональ ровна....Скачать

Что мы узнали?

Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Диагональ прямоугольника

Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.

Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.

Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.

Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Как найти диагональ прямоугольника

Воспользуемся теоремой Пифагора и формулой

d — диагональ квадрата

a — длина прямоугольника

b — ширина прямоугольника

Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.

Видео:Диагональ прямоугольника образует угол 50° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Диагональ прямоугольника онлайн калькулятор

Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.

Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.

Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Все формулы для треугольника

Видео:Диагонали трапеции и точка их пересеченияСкачать

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

Видео:Пробный ЕГЭ 2013 В6 диагональ прямоугольника ABCD #6Скачать

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):