Укажите номер верного утверждения.
1) Если противоположные углы выпуклого четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
2) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 100°.
3) Сумма двух противоположных углов четырехугольника не превосходит 180°.
4) Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.
Проверим каждое из утверждений.
1) «Если противоположные углы выпуклого четырехугольника попарно равны, то этот четырехугольник — параллелограмм.» — верно, это признак параллелограмма.
2) «Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 100°.» — неверно, сумма углов выпуклого четырёхугольника равна 360°, а не 300°.
3) «Сумма двух противоположных углов четырехугольника не превосходит 180°.» — неверно, сумма противоположных углов четырехугольника больше 180°.
4) «Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.» — неверно, средняя линия трапеции равна полусумме оснований, то есть 5.
Видео:№424. Докажите, что если не все углы выпуклого четырехугольника равны друг другуСкачать
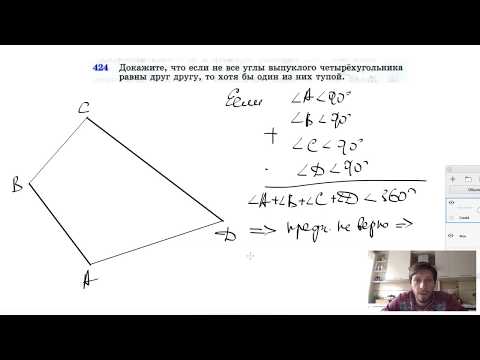
Укажите номер верного утверждения если противоположные углы выпуклого четырехугольника равны то
Какие из следующих утверждений верны? Запишите их номера без пробелов и других дополнительных символов в порядке возрастания.
1) Если противоположные углы выпуклого четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм.
2) Сумма двух противоположных углов четырёхугольника не превосходит 180 градусов
3) Если основания трапеции равны 4 и 6, то средняя линия равна 10
Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

Тест по теме: «Четырехугольники, площади» (геометрия, 8 класс)
Видео:№368. Найдите углы выпуклого четырехугольника, если они равны друг другу.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Тест по теме: «Четырехугольники, площади»
Основной целью данного теста является анализ геометрических высказываний, развитие критического мышления, а так же направлен на развитие способности анализировать и делать выводы.
Тест составлен в рамках подготовки к основному государственному экзамену (ОГЭ).
Работа состоит из 4 вариантов, одинакового уровня сложности. Каждый вариант содержит задания для экспресс-контроля знания теории (вопросы в этих задания сформулированы так, что проверяется не заучивание наизусть формулировок определений, свойств и теорем, а глубокое понимание теоретических положений курса геометрии по данной теме), а так же задачи базового уровня сложности.
Укажите номера верных утверждений:
1. В любом прямоугольнике диагонали взаимно перпендикулярны.
2. Существует квадрат, который не является ромбом.
3. Диагонали квадрата взаимно перпендикулярны.
4. Сумма углов выпуклого четырехугольника равна 180°.
5. Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
6. Диагонали квадрата делят его углы пополам.
7. Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
8. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник .
9. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
10. Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
11. Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160° .
12. Если площади фигур равны, то равны и сами фигуры.
13. Площадь трапеции равна произведению суммы оснований на высоту.
14. Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
15. Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10 .
16. Если диагонали ромба равны 3 и 4, то его площадь равна 6.
17. Площадь трапеции меньше произведения суммы оснований на высоту .
18. Площадь прямоугольного треугольника меньше произведения его катетов.
19. Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
20. Площадь трапеции равна половине высоты, умноженной на разность оснований.
21. Площадь прямоугольного треугольника равна половине произведения его катетов.
22. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
23. Диагонали прямоугольника равны.
24. У любой трапеции боковые стороны равны.
25. Диагональ трапеции делит её на два равных треугольника.
26. Диагонали ромба перпендикулярны .
Укажите номера верных утверждений:
1. Диагонали квадрата делят его углы пополам.
2. Площадь трапеции равна произведению суммы оснований на высоту.
3. Площадь прямоугольного треугольника меньше произведения его катетов.
4. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник .
5. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
6. Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
7. Диагональ трапеции делит её на два равных треугольника.
8. В любом прямоугольнике диагонали взаимно перпендикулярны.
9. Площадь трапеции равна половине высоты, умноженной на разность оснований.
10. Если диагонали ромба равны 3 и 4, то его площадь равна 6.
11. Диагонали ромба перпендикулярны .
12. Сумма углов выпуклого четырехугольника равна 180°.
13. Площадь прямоугольного треугольника равна половине произведения его катетов.
14. Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
15. Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
16. Диагонали квадрата взаимно перпендикулярны.
17. У любой трапеции боковые стороны равны.
18. Если площади фигур равны, то равны и сами фигуры.
19. Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
20. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
21. Диагонали прямоугольника равны.
22. Существует квадрат, который не является ромбом.
23. Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10 .
24. Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160° .
25. Площадь трапеции меньше произведения суммы оснований на высоту .
26. Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
Укажите номера верных утверждений:
1. Площадь трапеции равна половине высоты, умноженной на разность оснований.
2. Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
3. В любом прямоугольнике диагонали взаимно перпендикулярны.
4. Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160° .
5. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
6. Площадь трапеции меньше произведения суммы оснований на высоту .
7. Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
8. Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10 .
9. Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
10. Диагонали квадрата взаимно перпендикулярны.
11. Площадь трапеции равна произведению суммы оснований на высоту.
12. Диагонали прямоугольника равны.
13. Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
14. Диагонали ромба перпендикулярны .
15. Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
16. Существует квадрат, который не является ромбом.
17. Диагональ трапеции делит её на два равных треугольника.
18. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник .
19. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
20. Площадь прямоугольного треугольника меньше произведения его катетов.
21. Диагонали квадрата делят его углы пополам.
22. Если площади фигур равны, то равны и сами фигуры.
23. У любой трапеции боковые стороны равны.
24. Если диагонали ромба равны 3 и 4, то его площадь равна 6.
25. Сумма углов выпуклого четырехугольника равна 180°.
26. Площадь прямоугольного треугольника равна половине произведения его катетов.
Укажите номера верных утверждений:
1. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник .
2. У любой трапеции боковые стороны равны.
3. Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
4. Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
5. Площадь прямоугольного треугольника меньше произведения его катетов.
6. Диагональ трапеции делит её на два равных треугольника.
7. Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160° .
8. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
9. Сумма углов выпуклого четырехугольника равна 180°.
10. Площадь прямоугольного треугольника равна половине произведения его катетов.
11. Площадь трапеции меньше произведения суммы оснований на высоту .
12. Диагонали ромба перпендикулярны .
13. Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
14. В любом прямоугольнике диагонали взаимно перпендикулярны.
15. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
16. Диагонали прямоугольника равны.
17. Диагонали квадрата делят его углы пополам.
18. Если площади фигур равны, то равны и сами фигуры.
19. Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10 .
20. Если диагонали ромба равны 3 и 4, то его площадь равна 6.
21. Площадь трапеции равна половине высоты, умноженной на разность оснований.
22. Площадь трапеции равна произведению суммы оснований на высоту.
23. Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
24. Диагонали квадрата взаимно перпендикулярны.
25. Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
26. Существует квадрат, который не является ромбом.
💥 Видео
Если диагонали выпуклого четырёхугольника равны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Разбор Варианта ОГЭ Ларина №290 (№1-25) обычная версия ОГЭ-2022.Скачать

8 класс, 3 урок, ЧетырехугольникСкачать

№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

8 класс, 2 урок, Выпуклый многоугольникСкачать

Сумма углов выпуклого четырёхугольника равна 360°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Разбор Варианта ОГЭ Ларина №237 (№1-20) обычная версия ОГЭ-2020.Скачать

Задача 6 №27927 ЕГЭ по математике. Урок 142Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Задание 24 ОГЭ по математике. Геометрические фигуры. Сумма трех углов выпуклого четырехугольника 300Скачать

Геометрия Диагонали выпуклого четырехугольника равны 8 см и 12 см а угол между ними 30 НайдитеСкачать

Задание 14 (часть 1) | ВПР-8 2024 Математика | Анализ геометрических высказыванийСкачать

ВПР 2021 // Математика, 8 класс // Вариант №4, Часть 2 // Решение, ответыСкачать

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

Задание 14 (часть 2) | ВПР-8 2024 Математика | Анализ геометрических высказыванийСкачать

Разбор Варианта ОГЭ Ларина №219 (№1-20).Скачать

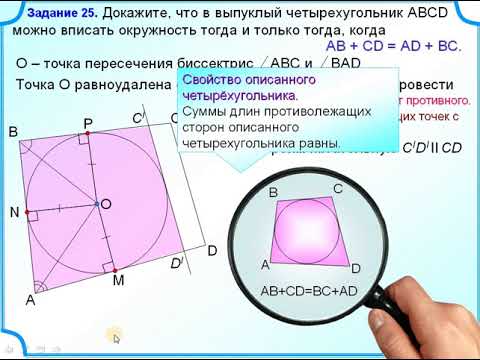
ОГЭ Задание 25 Доказательство от противногоСкачать