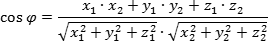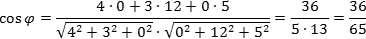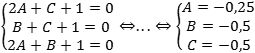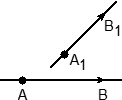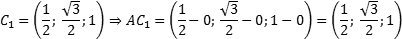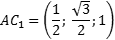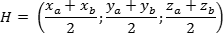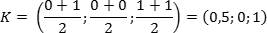Найдите координаты векторов в единичном кубе

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:

Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

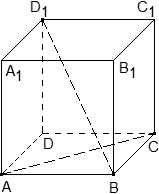
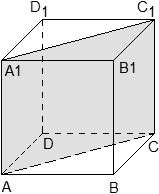
Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

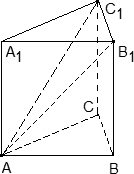
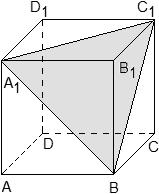
Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

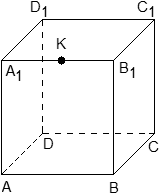
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

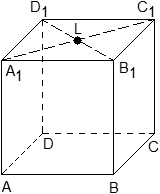
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Решение задач С2 методом координат

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Дорофеева Лилия Ильинична учитель математики МБОУ СОШ №6, г.Нижнекамск Республики Татарстан Решение задач С2 методом координат

Единичный куб z x y A (1; 0; 0) A1 (1; 0; 1) B (1; 1; 0) B1 (1; 1; 1) C (0; 1; 0) C1 (0; 1; 1) D (0; 0; 0) D1 (0; 0; 1)

Правильная треугольная призма c a х у z O

Прямоугольный параллелепипед z x y с b a A (a; 0; 0) A1 (a; 0; c) B (a; b; 0) B1 (a; b; c) C (0; b; 0) C1 (0; b; c) D (0; 0; 0) D1 (0; 0; c)

Прямоугольная шестиугольная призма z y x a b C B A a a D E F C(a; 0;0) C1 (a; 0;c) F (- a; 0;0) F1 (- a; 0;c)

Правильная четырёхугольная пирамида z y x a h

Правильная шестиугольная пирамида z x y C (a; 0;0) a h

Правильная треугольная призма х у z H a с

Правильная треугольная пирамида х y O z H h

Угол между прямой и плоскостью Прямая а образует с плоскостью угол . Плоскость задана уравнением: ах+ву+сz+d=0 и — вектор нормали, Синус угла определяется по формуле:

Угол между прямыми Вектор лежит на прямой а, Вектор лежит на прямой в. Косинус угла между прямыми а и в:

Угол между плоскостями 1.3. Угол между двумя плоскостями. Плоскость задана уравнением: и ее вектор нормали плоскость задана уравнением и ее вектор нормали . Косинус угла между плоскостями:

Расстояние от точки до плоскости Расстояние h от точки до плоскости , заданной уравнением ах+ву+сz+d=0 определяется по формуле:

Примеры решения задач 1. В единичном кубе найти угол между прямыми и х y z Введем систему координат и найдем координаты точек A (0; 0; 0), B (1; 0; 0) , B1 (1; 0; 1) , C1 (1; 1; 1) Находим координаты направляющих векторов прямых и по формуле 1. Косинус угла между прямыми определяется по формуле 1.1:

х z y 2.В правильной шестиугольной призме , все ребра которой равны 1, найти угол между прямой AF и плоскостью Плоскость совпадает с плоскостью грани ; зададим ее с помощью точек Уравнение плоскости примет вид Вектор нормали : Синус искомого угла: Введем систему координат и находим координаты нужных точек. Найдем координаты вектора Пусть ax+by+cz+d=0 – уравнение плоскости

3.В правильной четырехугольной пирамиде , все ребра которой равны 1, найти синус угла между прямой ВЕ и плоскостью SAD, где Е- середина ребра SC х y z Координаты точки Е определим по формуле 3: Пусть уравнение плоскости ADS ax+by+cz+d=0 Из того, что следует, что d=0, b+d=0 и : Отсюда получим, что и уравнение плоскости ADS примет вид: . Вектор нормали Синус угла между прямой ВЕ плоскостью ADS определим по формуле 1.2

х y z 4.В единичном кубе А… ,найти расстояние от точки А до прямой Находим координаты точек , вектора Искомое расстояние есть длина перпендикуляра АК. Если отрезок ВD разделен точкой K(x;y;z) в отношении , то координаты точки К определяются по формуле 1.5: К

5.В правильной шестиугольной призме , все ребра которой равны 1, найти расстояние от точки А до плоскости х y z Координаты точек Подставив координаты точек в общее уравнение плоскости получим систему уравнений: Уравнение плоскости примет вид: Вектор нормали: Вычислим расстояние h от точки А до плоскости по формуле 1.4:

6.В единичном кубе , найти расстояние между прямыми и х y z При параллельном переносе на вектор прямая отображается на прямую . Таким образом, плос-кость содержит прямую и параллельна прямой . Расстояние между прямыми и находим как расстояние от точки В до плоскости Пусть ax+by+cz+d=0 – уравнение плоскости . Так как Уравнение плоскости запишется как –сx-сy+cz=0, или х+у+z=0.. Вектор нормали Расстояние h от точки до плоскости находим по формуле

Литература: 1.Каталог задач: www.problems.ru 2.Образовательный портал»Физ/мат класс»: www.fmclass.ru 3.Открытый банк задач: www.mathege.ru 4.Федеральный институт педагогических измерений: www.fipi.ru

Краткое описание документа:

Существует два способа решения задач по стереометрии. Первый — классический ,требует отличного знания аксиом и теорем стереомет- рии, логики, умения построить чертеж и свести объемную задачу к планиметриче- ской. Способ хорош тем, что развивает мозги и пространственное воображение. Другой метод -применение векторов и координат. Это простые формулы, ал- горитмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить C2 хочется. Если вы освоили векторы на плоскости и действия с ними ,то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 931 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 496 018 материалов в базе

Дистанционные курсы для педагогов

Другие материалы

• 30.04.2014
• 7116

• 30.04.2014
• 4863

• 30.04.2014
• 1118

• 30.04.2014
• 1752

• 30.04.2014
• 883

• 30.04.2014
• 1583

• 30.04.2014
• 1353

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.04.2014 2560 —> —> —> —>
• PPTX 1.6 мбайт —> —>
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Дорофеева Лилия Ильинична. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет
• Подписчики: 1
• Всего просмотров: 8189
• Всего материалов: 9

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Санкт-Петербургский госуниверситет переходит на дистанционное обучение

Время чтения: 1 минута

Онлайн-семинар о снятии эмоционального напряжения у детей и подростков

Время чтения: 2 минуты

УрФУ возглавил рейтинг медиаактивности вузов

Время чтения: 1 минута

Число иностранных студентов в РФ увеличилось за три года

Время чтения: 1 минута

Орловские школы переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Школы Сургута переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.