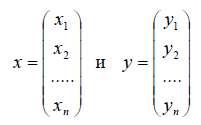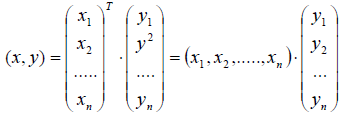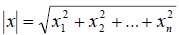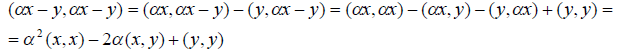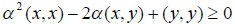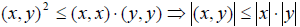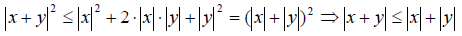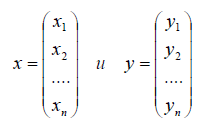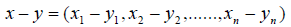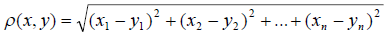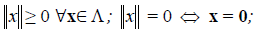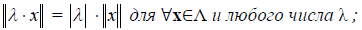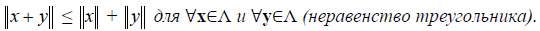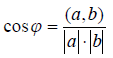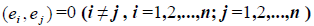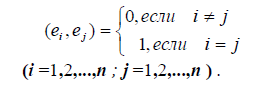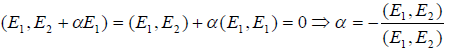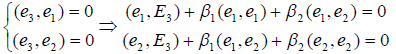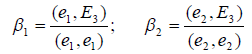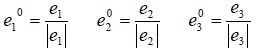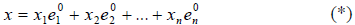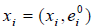Треугольник в евклидовом пространстве (7 видео)

Пространство треугольников

Алексей Панов, Дмитрий Ал. Панов, Пётр Панов
«Квантик» №1, 2021

Треугольник — основной объект геометрии, а может, и математики вообще. Собранные все вместе, треугольники образуют некоторое пространство — Треугольный Мир. Мы составим его подробную карту, побываем на окраинах этого мира и раскроем тайну его полюсов. Подготовку к большому путешествию начнём с простых измерений.

Содержание

Измерения
Неравенство треугольника
Перестановки
Три числа — это цвет
Ещё две карты
Евклидово пространство
Определение евклидова пространства
Неравенство Коши-Буняковского
Неравенство треугольника
Норма евклидова пространства
Угол между векторами
Ортонормированный базис
Треугольник в евклидовом пространстве
🎥 Видео

Видео:§47 Евклидово пространствоСкачать

Измерения

Нарисуйте на листе бумаги равносторонний треугольник с высотой 1 дециметр.

Рис. 1. Процесс измерения ставит в соответствие каждой точке T три числа a, b, c — длины отрезков, перпендикулярных сторонам треугольника

Отметьте внутри него точку, опустите из неё три перпендикуляра на стороны треугольника — на рисунке 1 они обозначены a, b, c — и подсчитайте их суммарную длину a + b + c (в дециметрах). Проделайте несколько таких экспериментов, выбирая разные точки внутри треугольника, и заполните журнал измерений.

Вы получите удивительный результат: a + b + c всегда равно 1. Дело в том, что в равностороннем треугольнике сумма перпендикуляров, опущенных из точки внутри треугольника на его стороны, равна высоте треугольника.

Видео:Математика это не ИсламСкачать

Неравенство треугольника

Раз уж у нас получились три отрезка длины a, b и c, почему бы не попытаться составить из них треугольник с этими сторонами?

Упражнение 2. Можно ли составить треугольник из отрезков длины 1, 2, 4; 1, 2, 3; 2, 3, 4?

Оказывается, треугольник со сторонами a, b и c существует только в том случае, когда одновременно выполняются три неравенства треугольника a Рис. 2. Пространство треугольников

Для каких же точек T внутри ABC большее из чисел a, b, c меньше суммы двух других?

Разобьём наш треугольник ABC на четыре маленьких (рис. 2). Вершины среднего из них расположены в серединах сторон ABC. Только для точек внутри этого серединного треугольника, то есть для соответствующих им троек чисел a, b, c, выполняются все три неравенства a Рис. 3. Три пункта на карте Треугольного Мира

Нанесём на карту Треугольного Мира первые пункты. Начнём с равностороннего треугольника периметра 1, в нём ( a = frac ), ( b = frac ), ( c = frac ). Выберем ещё известный египетский треугольник со сторонами a = 3, b = 4, c = 5. Сам треугольник, конечно, нельзя разместить на карте, но подобный ему со сторонами ( a = frac ), ( b = frac ), ( c = frac ), то есть ( frac ), ( frac ), ( frac ), — уже можно. Добавим ещё третий пункт — равнобедренный треугольник со сторонами ( a = frac ), ( b = frac ), ( c = frac ). И вот первые наблюдения: равносторонний треугольник соответствует центру Треугольного Мира, равнобедренный треугольник со сторонами ( frac ), ( frac ), ( frac ) расположен близко к стороне AC и одинаково удалён от сторон AB и BC (рис. 3). Пойдём дальше.

Видео:Three-Point Equidistant ProjectionСкачать

Перестановки

Стороны треугольника можно записать в разном порядке. Задают ли эти записи (перестановки) одну и ту же точку на нашей карте или разные?

Упражнение 4. Сколько существует разных перестановок а) трёх различных чисел; б) трёх чисел, два из которых равны; в) трёх одинаковых чисел?

Рис. 4. На карте Треугольного Мира каждый треугольник, у которого все стороны разные, присутствует 6 раз, равнобедренный — 3 раза, а равносторонний — один

На рисунке 3 зелёная точка обозначает треугольник со сторонами ( frac ), ( frac ), ( frac ). На рисунке 4 зелёных точек шесть — они соответствуют всем возможным перестановкам чисел ( frac ), ( frac ), ( frac ).

Для чисел ( frac ), ( frac ), ( frac ), отвечающих равнобедренному треугольнику, есть три различные перестановки. Им соответствуют три синие точки на рисунке 4. Набор чисел ( frac ), ( frac ), ( frac ) уникален. Итак, порядок, в котором перечислены длины сторон, на карте учитывается.

Взглянем ещё раз на рисунок 4. Там вершины внутреннего треугольника получили новые названия R , G , B , а внешний треугольник слегка поблёк — это мы готовимся к увеличению размеров нашей карты и к её раскраске. Далее мы не будем изображать внешний треугольник и сосредоточимся исключительно на нашей карте, а именно, на треугольнике R G B .

Видео:Угол между векторами. 9 класс.Скачать

Три числа — это цвет

Рис. 5. Раскраска треугольного мира

Для нас три числа a, b, c — это, прежде всего, треугольник, но три числа — это ещё и цвет. Мы имеем в виду R G B -палитру. В ней все цвета получаются смешением трёх основных — красного, зелёного и синего, — и цвет задаётся набором из трёх чисел ( r , g , b ), каждое из которых заключено в пределах от 0 до 1. Например, (0, 0, 0) — это чёрный, (1, 1, 1) — белый, а (( frac, frac, frac )) — оттенок серого. Сами красный, зелёный и синий — это, конечно же, (1, 0, 0), (0, 1, 0), (0, 0, 1). Тройку чисел, задающую цвет, мы пишем в скобках, чтобы не путать её с точкой Треугольного Мира.

Было бы естественно раскрасить точку нашего Треугольного Мира, отвечающую числам a, b, c, тем же самым цветом ( a , b , c ). Но такая раскраска, к сожалению, малоконтрастная и недостаточно яркая. Вот если её рассчитать как ( 1 − 2a , 1 − 2b , 1 − 2c ), то всё встаёт на свои места и, главное, вершины R , G , B приобретают свои законные цвета (рис. 5).

Упражнение 5. Рассчитайте, каким R G B -цветом раскрашен центр Треугольного Мира.

Видео:§48 Ортонормированный базис евклидова пространстваСкачать

Ещё две карты

Разные типы карт расширяют наши представления об окружающем мире. Вот карта, на которой обозначена сеть точек, равномерно заполняющая наш Треугольный Мир (рис. 6).

Упражнение 6. Найдите на рисунке 6 центр Треугольного Мира и проверьте решение упражнения 5.

Рис. 6. Сеть точек, равномерно заполняющая Треугольный Мир

А на рисунке 7 цветные точки заменены маленькими треугольниками, которым они соответствуют.

Не правда ли, эти треугольники похожи на маленькие магнитные стрелки с тремя концами, указывающими на вершины треугольника R G B ?

На этом мы временно прерываем наше изложение. Нам ещё предстоит путешествие к отдалённым окраинам Треугольного Мира и к его полюсам, тайну которых мы попытаемся раскрыть.

А пока посмотрите картинки в большом тексте Кая Беренда «Введение в алгебраические стеки» (K. Behrend, Introduction to Algebraic Stacks). В нём подробно изучаются многочисленные Треугольные Миры. Наш Треугольный Мир фигурирует там под названиями ( mathscr ) или ( mathscr<overline> ). Рекомендуем первые 70 страниц, где содержится множество картинок. Одну из них мы воспроизвели на рисунке 7, слегка улучшив её.

Рис. 7. Каждая точка рисунка 6 заменена треугольником

Ещё одно изображение (рис. 6) мы взяли из статьи П. Панова «О геометрических медианах треугольников». Там тоже много цветных картинок!

Видео:✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать

Евклидово пространство

Видео:НЕЕВКЛИДОВАЯ ГЕОМЕТРИЯ. оказывается это так просто...Скачать

Определение евклидова пространства

Определение 1. Вещественное линейное пространство называется евклидовым, если в нём определена операция, ставящая в соответствие любым двум векторам x и y из этого пространства число, называемое скалярным произведением векторов x и y и обозначаемое (x,y) , для которого выполнены условия:

2. (x + y,z) = (x,z) + (y,z) , где z — любой вектор, принадлежащий данному линейному пространству;

3. ( x,y) = (x,y) , где — любое число;

4. (x,x) 0 , причём (x,x) = 0 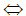x = 0.

Например, в линейном пространстве одностолбцовых матриц скалярное произве дение векторов

можно определить формулой

Евклидово пространство размерности n обозначают E n . Заметим, что существуют как конечномерные, так и бесконечномерные евклидовы пространства.

Определение 2. Длиной (модулем) вектора x в евклидовом пространстве E n называют (x,x) и обозначают её так: |x| = (x,x) . У всякого вектора евклидова пространства существует длина, причём у нулевого вектора она равна нулю.

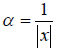
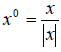
Умножая ненулевой вектор x на число , мы получим вектор , длина которого равна единице. Эта операция называется нормированием вектора x.

Например, в пространстве одностолбцовых матриц длину вектора 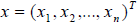можно определить формулой:

Видео:Лобачевский против Евклида: две геометрии одного мираСкачать

Неравенство Коши-Буняковского

Пусть x E n и y E n – любые два вектора. Докажем, что для них имеет место неравенство:

(Неравенство Коши-Буняковского)

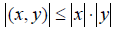
Доказательство. Пусть — любое вещественное число. Очевидно, что ( x y, x y) 0. С другой стороны, в силу свойств скалярного произведения можем написать

Получили, что

Дискриминант этого квадратного трёхчлена не может быть положительным, т.е. 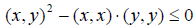, откуда вытекает:

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Неравенство треугольника

Пусть x и y — произвольные векторы евклидова пространства E n , т.е. x E n и y E n .

Докажем, что 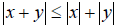. (Неравенство треугольника).

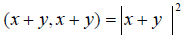
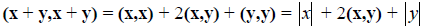
Доказательство. Очевидно, что С другой стороны, . Принимая во внимание неравенство Коши-Буняковского, получим

Неравенство треугольника доказано.

Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Норма евклидова пространства

Определение 1. Линейное пространство называется метрическим, если любым двум элементам этого пространства x и y поставлено в соответствие неотрицательное число (x,y) , называемое расстоянием между x и y , ( (x,y) 0) , причём выполняются условия (аксиомы):

1) (x,y) = 0 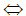x = y

3) для любых трёх векторов x, y и z этого пространства (x,y) (x,z) + (z,y).

Замечание. Элементы метрического пространства обычно называют точками.

Евклидово пространство E n – метрическое, причём в качестве расстояния между векторами x E n и y E n можно взять x y.

Так, например, в пространстве одностолбцовых матриц, где

получим

следовательно

Определение 2. Линейное пространство называется нормированным, если каждому вектору x из этого пространства поставлено в соответствие неотрицательное число, называемое его нормой x. При этом выполняются аксиомы:

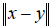
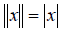
Нетрудно видеть, что нормированное пространство является метрическим простран ством. В самом деле, в качестве расстояния между x и y можно взять . В евклидовом пространстве E n в качестве нормы любого вектора x E n принимается его длина, т.е. .

Итак, евклидово пространство E n является метрическим пространством и более того, евклидово пространство E n является нормированным пространством.

Видео:Неевклидова геометрия #shorts #nonEuclideangeometry #lobachevskyСкачать

Угол между векторами

Определение 1. Углом между ненулевыми векторами a и b евклидова простран ства E n называют число 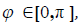для которого

Определение 2. Векторы x и y евклидова пространства E n называются ортогона льными, если для них выполняется равенство (x,y) = 0.

Если x и y — ненулевые, то из определения следует, что угол между ними равен

Заметим, что нулевой вектор по определению считается ортогональным любому вектору.

Пример. В геометрическом (координатном) пространстве 3, которое является частным случаем евклидова пространства, орты i, j и k взаимно-ортогональны.

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Ортонормированный базис

Определение 1. Базис e 1 ,e 2 . e n евклидова пространства E n называется ортогона льным, если векторы этого базиса попарно ортогональны, т.е. если

Определение 2. Если все векторы ортогонального базиса e 1 , e 2 . e n единичны, т.е. e i = 1 (i = 1,2. n ) , то базис называется ортонормированным, т.е. для ортонормированного базиса

Теорема. (о построении ортонормированного базиса)

Во всяком евклидовом пространстве E n существуют ортонормированные базисы.

Доказательство. Докажем теорему для случая n = 3.

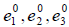
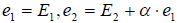
Пусть E 1 ,E 2 ,E 3 — некоторый произвольный базис евклидова пространства E 3 Построим какой-нибудь ортонормированный базис в этом пространстве. Положим , где — некоторое вещественное число, которое выберем таким образом, чтобы было (e 1 ,e 2 ) = 0, тогда получим

причём очевидно, что = 0 , если E 1 и E 2 ортогональны, т.е. в этом случае e 2 = E 2 , а 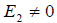, т.к. это базисный вектор.

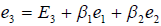
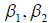
Далее, определим вектор e 3 равенством , причём числа определяется из условия ортогональности вектора e 3 с векторами e 1 ,e 2 , т.е.

Учитывая, что (e 1 ,e 2 ) = 0, получим

Очевидно, что 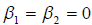, если e 1 и e 2 ортогональны с вектором E 3 , т.е. в этом случае следует взять e 3 = E 3 . Вектор E 3 0 , т.к. E 1 , E 2 и E 3 линейно независимы, следовательно e 3 0.

Кроме того, из приведённого рассуждения следует, что e 3 нельзя представить в виде линейной комбинации векторов e 1 и e 2 , следовательно векторы e 1 , e 2 , e 3 линейно незави симы и попарно ортогональны, следовательно, их можно взять в качестве базиса евклидова пространства E 3 . Остаётся только пронормировать построенный базис, для чего достаточно каждый из построенных векторов разделить на его длину. Тогда получим

Итак, мы построили базис 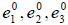— ортонормированный базис. Теорема доказана.

Применённый способ построения ортонормированного базиса из произвольного базиса называется процессом ортогонализации. Заметим, что в процессе доказательства теоремы мы установили, что попарно ортогональные векторы линейно независимы. Кроме того, если 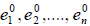— ортонормированный базис в E n , тогда для любого вектора x E n имеет место единственное разложение

где x 1 , x 2 . x n — координаты вектора x в этом ортонормированном базисе.

то умножив скалярно равенство (*) на , получим .

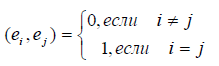
В дальнейшем мы будем рассматривать только ортонормированные базисы, а потому для простоты их записи нолики сверху у базисных векторов мы будем опускать.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Треугольник в евклидовом пространстве

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Евклидовы пространства Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

Глава 4
ЕВКЛИДОВЫ ПРОСТРАНСТВА

Из курса аналитической геометрии читатель знаком с понятием скалярного произведения двух свободных векторов и с четырьмя основными свойствами указанного скалярного произведения. В настоящей главе изучаются линейные пространства любой природы, для элементов которых каким-либо способом (причем безразлично каким) определено правило, ставящее в соответствие любым двум элементам число, называемое скалярным произведением этих элементов. При этом важно только, чтобы это правило обладало теми же четырьмя свойствами, что и правило составления скалярного произведения двух свободных векторов. Линейные пространства, в которых определено указанное правило, называются евклидовыми пространствами. В настоящей главе выясняются основные свойства произвольных евклидовых пространств.

§ 1. Вещественное евклидово пространство и его простейшие свойства

1. Определение вещественного евклидова пространства. Вещественное линейное пространство R называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования.
I. Имеется правило, посредством которого любым двум элементам этого пространства х и у ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом (х, у).
П. Указанное правило подчинено следующим четырем аксиомам:
1°. (х, у) = (у, х) (переместительное свойство или симметрия);
2°. (x₁ + x 2, у) = (х₁ , у) + (х₂, у) (распределительное свойство);
3°. ( λ х, у) = λ (х, у) для любого вещественного λ ;
4°. (х, х) > 0, если х — ненулевой элемент; (х, х) = 0, если х — нулевой элемент.
Подчеркнем, что при введении понятия евклидова пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов, произведения элемента на число и скалярного произведения элементов (важно лишь, чтобы эти правила удовлетворяли восьми аксиомам линейного пространства и четырем аксиомам скалярного произведения).
Если же природа изучаемых объектов и вид перечисленных правил указаны, то евклидово пространство называется конкретным.
Приведем примеры конкретных евклидовых пространств.
Пример 1. Рассмотрим линейное пространство В₃, всех свободных векторов. Скалярное произведение любых двух векторов определим так, как это было сделано в аналитической геометрии (т. е. как произведение длин этих векторов на косинус угла между ними). В курсе аналитической геометрии была доказана справедливость для так определенного скалярного произведения аксиом 1°- 4° (см. выпуск «Аналитическая геометрия», гл.2, §2, п.З). Стало быть, пространство В₃ с так определенным скалярным произведением является евклидовым пространством.
Пример 2. Рассмотрим бесконечномерное линейное пространство С [а, b ] всех функций x(t), определенных и непрерывных на сегменте а ≤ t ≤ b . Скалярное произведение двух таких функций x(t) и y(t) определим как интеграл (в пределах от а до b ) от произведения этих функций

Элементарно проверяется справедливость для так определенного скалярного произведения аксиом 1°-4°. В самом деле, справедливость аксиомы 1° очевидна; справедливость аксиом 2° и 3° вытекает из линейных свойств определенного интеграла; справедливость аксиомы 4° вытекает из того, что интеграл от непрерывной неотрицательной функции x 2 (t) неотрицателен и обращается в нуль лишь тогда, когда эта функция тождественно равна нулю на сегменте а ≤ t ≤ b (см. выпуск «Основы математического анализа», часть I, свойства 1° и 2° из п. 1 §6 гл. 10) (т.е. является нулевым элементом рассматриваемого пространства).
Таким образом, пространство С [а, b ] с так определенным скалярным произведением представляет собой бесконечномерное евклидово пространство.
Пример 3. Следующий пример евклидова пространства дает n-мерное линейное пространство А _n упорядоченных совокупностей n вещественных чисел, скалярное произведение двух любых элементов х= (х₁, x₂. х_n) и у = ( y ₁, y ₂. y _n) которого определяется равенством

Справедливость для так определенного скалярного произведения аксиомы 1° очевидна; справедливость аксиом 2° и 3° легко проверяется достаточно вспомнить определение операций сложения элементов и умножения их на числа:

наконец, справедливость аксиомы 4° вытекает из того, что (х, х) = х₁ 2 + x₂ 2 + . + х_n 2 всегда является неотрицательным числом и обращается в нуль лишь при условии х₁ = х₂ = . = х _n = 0.
Рассмотренное в этом примере евклидово пространство часто обозначают символом Е _n .
Пример 4. В том же самом линейном пространстве А _n введем скалярное произведение любых двух элементов х= (х₁, x₂. х_n) и у = ( y ₁, y ₂. y _n) не соотношением (4.2), а другим, более общим, способом.
Для этого рассмотрим квадратную матрицу порядка n

Составим с помощью матрицы (4.3) однородный многочлен второго порядка относительно n переменных х₁, x₂. х_n

Забегая вперед, отметим, что такой многочлен называется квадратичной формой (порождаемой матрицей (4.3)) ( квадратичные формы систематически изучаются в гл. 7 этой книги).
Квадратичная форма (4.4) называется положительно определенной, если она принимает строго положительные значения для всех значений переменных х₁, x₂. х_n , одновременно не равных нулю (в гл. 7 этой книги будет указано необходимое и достаточное условие положительной определенности квадратичной формы).
Так как при х₁ = х₂ = . = х _n = 0 квадратичная форма (4.4), очевидно, равна нулю, то можно сказать, что положительно определенная
квадратичная форма обращается в нуль лишь при условии х₁ = х₂ = . = х _n = 0.
Потребуем, чтобы матрица (4.3) удовлетворяла двум условиям.
1°. Порождала положительно определенную квадратичную форму (4.4).
2°. Была симметричной (относительно главной диагонали), т.е. удовлетворяла условию a_ik = а _ki для всех i = 1, 2. n и k = I, 2. n .
С помощью матрицы (4.3), удовлетворяющей условиям 1° и 2°, определим скалярное произведение двух любых элементов х= (х₁, x₂. х_n) и у = ( y ₁, y ₂. y _n) пространства А _n соотношением

Легко проверить справедливость для так определенного скалярного произведения всех аксиом 1°-4°. В самом деле, аксиомы 2° и 3°, очевидно, справедливы при совершенно произвольной матрице (4.3); справедливость аксиомы 1° вытекает из условия симметричности матрицы (4.3), а справедливость аксиомы 4° вытекает из того, что квадратичная форма (4.4), представляющая собой скалярное произведение (х, х), является положительно определенной.
Таким образом, пространство А _n со скалярным произведением, определяемым равенством (4.5), при условии симметричности матрицы (4.3) и положительной определенности порождаемой ею квадратичной формы, является евклидовым пространством.
Если в качестве матрицы (4.3) взять единичную матрицу, то соотношение (4.4) перейдет в (4.2), и мы получим евклидово пространство Е _n , рассмотренное в примере 3.
2. Простейшие свойства произвольного евклидова пространства. Устанавливаемые в этом пункте свойства справедливы для совершенно произвольного евклидова пространства как конечной, так и бесконечной размерности.
Теорема 4.1. Для любых двух элементов х и у произвольного евклидова пространства справедливо неравенство

( x, y ) 2 ≤ ( x, x )( y, y ), (4.6)

называемое неравенством Коши-Буняковского.
Доказательство. Для любого вещественного числа λ , в силу аксиомы 4° скалярного произведения, справедливо неравенство ( λ х — у, λ х — у) > 0. В силу аксиом 1°-3°, последнее неравенство можно переписать в виде

λ 2 (x, x) — 2 λ (x, y) + (y, y) ≤ 0

Необходимым и достаточным условием неотрицательности последнего квадратного трехчлена является неположительность его дискриминанта, т. е. неравенство (в случае (х, х) = 0 квадратный трехчлен вырождается в линейную функцию, но в этом случае элемент х является нулевым, так что (х, у) = 0 и неравенство (4.7) также справедливо)

( x, y ) 2 — ( x, x )( y, y ) ≤ 0. (4.7)

Из (4.7) сразу же вытекает неравенство (4.6). Теорема доказана.
Наша очередная задача — ввести в произвольном евклидовом пространстве понятие нормы (или длины) каждого элемента. Для этого введем понятие линейного нормированного пространства.
Определение. Линейное пространство R называется нормированным, если выполнены следующие два требования.
I. Имеется правило, посредством которого каждому элементу х пространства R ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое символом ||х||.
П. Указанное правило подчинено следующим трем аксиомам:
1°. ||х|| > 0, если х — ненулевой элемент; ||х|| = 0, если х — нулевой элемент;
2°. || λ х|| = | λ | ||х|| для любого элемента х и любого вещественного числа λ ;
3°. для любых двух элементов х и у справедливо следующее неравенство

называемое неравенством треугольника (или неравенством Минковского).
Теорема 4.2. Всякое евклидово пространство является нормированным, если норму любого элемента х в нем определить равенством

Доказательство. Достаточно доказать, что для нормы, определенной соотношением (4.9), справедливы аксиомы 1°-3° из определения нормированного пространства.
Справедливость для нормы аксиомы 1° сразу вытекает из аксиомы 4° скалярного произведения. Справедливость для нормы аксиомы 2° почти непосредственно вытекает из аксиом 1° и 3° скалярного произведения.
Остается убедиться в справедливости для нормы аксиомы 3°, т. е. неравенства (4.8). Будем опираться на неравенство Коши-Буняковского (4.6), которое перепишем в виде

С помощью последнего неравенства, аксиом 1°-4° скалярного произведения и определения нормы получим

Теорема доказана.
Следствие. Во всяком евклидовом пространстве с нормой элементов, определяемой соотношением (4.9), для любых двух элементов х и у справедливо неравенство треугольника (4.8).

Заметим далее, что в любом вещественном евклидовом пространстве можно ввести понятие угла между двумя произвольными элементами х и у этого пространства. В полной аналогии с векторной алгеброй, мы назовем углом φ между элементами х и у тот (изменяющийся в пределах от 0 до π ) угол, косинус которого определяется соотношением

Данное нами определение угла корректно, ибо в силу неравенства Коши-Буняковского (4.7′) дробь, стоящая в правой части последнего равенства, по модулю не превосходит единицы.
Далее договоримся называть два произвольных элемента х и у евклидова пространства Е ортогональными, если скалярное произведение этих элементов (х, у) равно нулю (в этом случае косинус угла ( φ между элементами х и у будет равен нулю).
Снова апеллируя к векторной алгебре, назовем сумму х + у двух ортогональных элементов х и у гипотенузой прямоугольного треугольника, построенного на элементах х и у.
Заметим, что во всяком евклидовом пространстве справедлива теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В самом деле, поскольку х и у ортогональны и (х, у) = 0, то в силу аксиом и определения нормы

||х + y || 2 = ( x+y, x+y ) = ( x, x ) + 2( x, y ) + (y, y) = (x,x) + (y, y) = ||х|| 2 + || y || 2 .

Этот результат обобщается и на n попарно ортогональных элементов х₁, x₂. х_n: если z = х₁ + x₂ + . + х_n, то

В заключение запишем норму, неравенство Коши-Буняковского и неравенство треугольника в каждом из конкретных евклидовых пространств, рассмотренных в предыдущем пункте.
В евклидовом пространстве всех свободных векторов с обычным определением скалярного произведения норма вектора а совпадает с его длиной |а|, неравенство Коши-Буняковского приводится к виду (( a,b ) 2 ≤ |а| 2 | b | 2 , а неравенство треугольника — к виду |a + b| ≤ |а| + | b | (Если сложить векторы а и b по правилу треугольника, то это неравенство тривиально сводится к тому, что одна сторона треугольника не превосходит суммы двух других его сторон).
В евклидовом пространстве С [а, b ] всех непрерывных на сегменте а ≤ t ≤ b функций х = x(t) со скалярным произведением (4.1) норма элемента х = x(t) равна , а неравенства Коши-Буняковского и треугольника имеют вид

Оба эти неравенства играют важную роль в различных разделах математического анализа.
В евклидовом пространстве Е _n упорядоченных совокупностей n вещественных чисел со скалярным произведением (4.2) норма любого элемента х = (х₁, x₂. х_n) равна

а неравенства Коши-Буняковского и треугольника имеют вид

Наконец, в евклидовом пространстве упорядоченных совокупностей n вещественных чисел со скалярным произведением (4.5) норма любого элемента х = (х₁, x₂. х_n) равна 0 (напоминаем, что при этом матрица (4.3) симметрична и порождает положительно определенную квадратичную форму (4.4)).