Видео:Геометрия В треугольнике ABC медианы BM и CK перпендикулярны и пересекаются в точке O. НайдитеСкачать
Ваш ответ
Видео:№571. В треугольнике ABC медианы АА1 и ВВ1 пересекаются в точке О. Найдите площадьСкачать
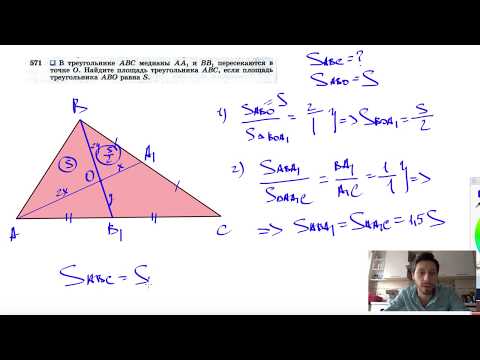
решение вопроса
Видео:Точка пересечения медиан в треугольникеСкачать
Похожие вопросы
- Все категории
- экономические 43,285
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,101
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Геометрия Медианы AD и BM треугольника ABC пересекаются в точке O Через точку O проведена прямаяСкачать
Медиана треугольника
Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.
На рисунке 1 медианой является отрезок BD .
Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).
Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),
и заметим, что (см. раздел нашего справочника «Площадь треугольника»)
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.
Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).
Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).
Теперь рассмотрим четырёхугольник FEDG (рис. 5).
Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,
Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,
Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.
Следствие . Все три медианы треугольника пересекаются в одной точке.
Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).
Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.
Определение . Точку пересечения медиан треугольника называют центроидом треугольника.
Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).
Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна 
площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).
Видео:Геометрия Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MBСкачать
В треугольнике abc медианы пересекаются
Задание 16. Медианы AM и BN треугольника ABC перпендикулярны и пересекаются в точке Р.
а) Докажите, что CP = АВ.
б) Найдите площадь треугольника ABC, если известно, что АС = 3 и ВС = 4.
а) Рассмотрим треугольник ABC, в котором отмечены медианы AM, BN и CF. Медианы пересекаются в одной точке P и делятся этой точкой в отношении 2:1, считая от вершины. То есть можно записать, что CP=2FP. Учитывая, что точка F находится на середине отрезка AB и треугольник APB прямоугольный (по условию задания), то точка F является центром описанной окружности вокруг треугольника APB. Следовательно, отрезки AF, FB, FP – радиусы этой окружности, и AB=2FP. Но так как 2FP=2PC, то AB=PC.
б) Пусть 
и 
, соответственно, 
и 
. Рассмотрим прямоугольный треугольник BPM (так как 
). В соответствии с теоремой Пифагора можно записать равенство:
Аналогично, из прямоугольного треугольника APN, имеем:
Получаем систему уравнений:
Умножим второе уравнение на 4 и вычтем его из первого, получим:
Подставляя полученное значение в первое уравнение, имеем:
Рассмотрим прямоугольный треугольник APB, в котором гипотенуза AB равна
Найдем косинус угла 
из треугольника ABC по теореме косинусов:
.
Наконец, площадь треугольника ABC равна:
Ответ: 
.
🔍 Видео
В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1/3 AB. РЕШЕНИЕ!Скачать
Медианы треугольника пересекаются в точке М. Свойство пересекающихся хорд.Скачать
9 класс. Геометрия.Скачать
Построение медианы в треугольникеСкачать
Геометрия В равнобедренном треугольнике ABC с основанием AC медианы AM и CK пересекаются в точке OСкачать
Медианы треугольника пересекаются в точке . Найдите длину медианыСкачать
Геометрия Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MBСкачать
№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать
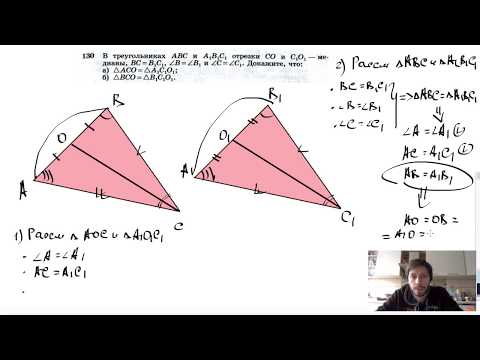
№130. В треугольниках ABC и А1В1С1 отрезки СО и С1О1 — медианы, ВС=В1С1, ∠B = ∠B1 и ∠C=∠C1Скачать
Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать
8. Медиана треугольника и её свойства.Скачать
В треугольнике ABC медианы AA1 и CC1 равны соответственно 12 и 15Скачать
Чему равна сторона треугольника, у которого медианы пересекаются под прямым угломСкачать
Геометрия В треугольнике ABC проведены медианы AL и FC, пересекающиеся в точке O. Найдите площадьСкачать
№369. Медианы грани ABC тетраэдра ОABC пересекаются в точке М. Разложите вектор ОАСкачать
