Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии.
- Немного истории
- Вступление
- Немного теории о векторах
- А теперь займемся практикой
- Векторы в C++: для начинающих
- Что такое вектор (vector)
- Как создать вектор (vector) в C++
- Второй способ обратиться к ячейке
- Как указать количество ячеек для вектора
- Как сравнить два вектора
- Как использовать вектор (vecto) в C++
- Класс и объекты
- Класс Vector
- Создание экземпляра вектора
- Перегрузка функции
- Построение вектора
- Конструирование с инициализацией
- Назначение вектора во время Construction
- const Vector
- Конструирование с помощью Iterator
- Уничтожение вектора
- Емкость вектора
- Присвоение значения с помощью нижнего индекса
- Присвоение значения с помощью функции at ()
- Проблема с подпрограммами
- Доступ к векторным данным
- Возвращение итераторов и вектора
- Обратная итерация
- Векторные модификаторы
- Операторы равенства и отношения для векторов
Немного истории
Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.
В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).
Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».
Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.
Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.
Вступление
«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».
Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.
Немного теории о векторах
Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.
Скалярное произведение векторов
Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b) 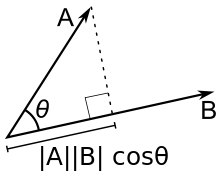
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то скалярное произведение (a, b) = x1x2 + y1y2.
Косое произведение векторов
Псевдоскалярным или косым произведением векторов на плоскости называется число
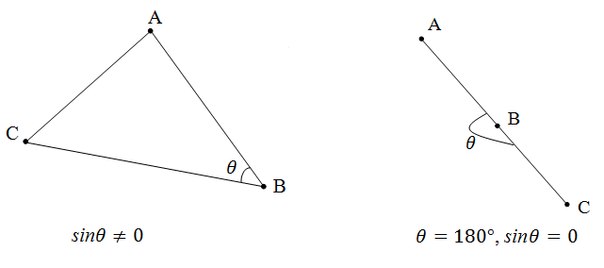
[a, b] = |a||b|sinθ
где 
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то косое произведение [a, b] = x1y2 — x2y1.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.
А теперь займемся практикой
Начнем с треугольников
Задача №1
Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.
Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.
Задача №2
Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.
Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x1, y1), B(x2, y2) вычисляется по формуле √(x1-x2) 2 +(y1-y2) 2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.
Задача №3
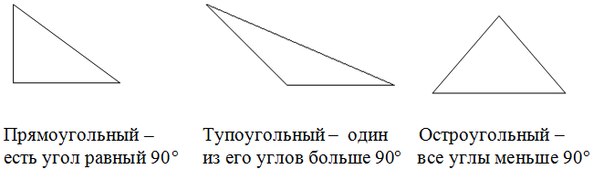
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.
Решение
Вспомним, что представляют собой каждый вид треугольника.
Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:
- Угол больше 90° – треугольник тупоугольный
- Угол меньше 90°– треугольник остроугольный
- Угол равен 90°– треугольник прямоугольный
Воспользуемся теоремой косинусов:
Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°. Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
- Если cosα > 0, то a 2 2 + c 2 – треугольник остроугольный
- Если cosα = 0, то a 2 = b 2 + c 2 – треугольник прямоугольный
- Если cosα 2 > b 2 + c 2 – треугольник тупоугольный
где a – большая сторона.
Задача №4
Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.
Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.
Задача №5
По данным сторонам треугольника найти его площадь.
Решение
Очевидно решение, заключается в применение формулы Герона. 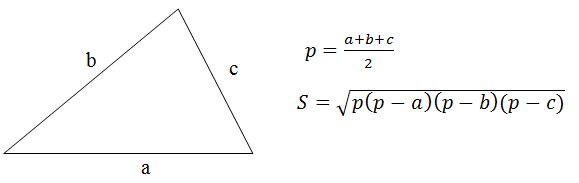
Кстати, никого не интересовало доказательство этой формулы?
Задача №6
Вычислить площадь треугольника заданного координатами своих вершин.
Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x1, y1), b(x2, y2) 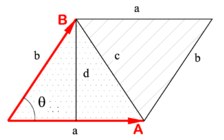
S = (x1y2 — x2y1) / 2 — ориентированная площадь треугольника
Задача №7
Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.
Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.
Метод площадей
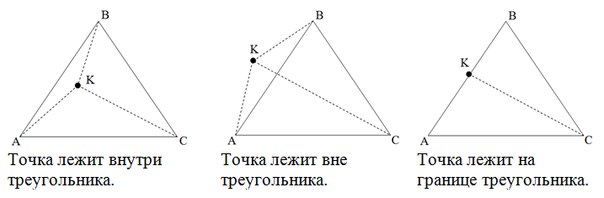
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.
Проверка полуплоскостей
Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника. 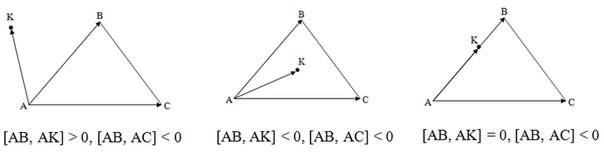
В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.
Задача №8
Вычисление площади многоугольника заданного координатами своих вершин.
Решение
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.
Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.
Метод трапеций
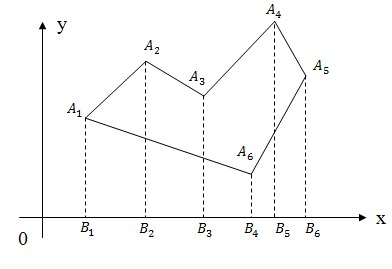
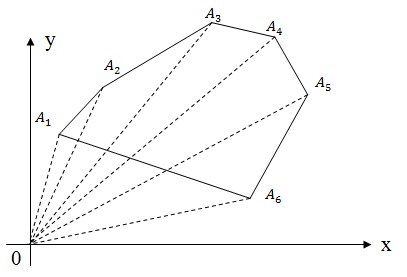
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = SA1 A2 B2 B1 + SA2 A3 B3 B2 + SA3 A4 B5 B3 + SA4 A5 B6 B5 + SA5 A6 B4 B6 + SA6 A1 B1 B4
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
SA1 A2 B2 B1 = 0.5 * (A1B1 + A2B2) *(B2 — B1)
Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.
Метод треугольников
Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть.
Задача №9
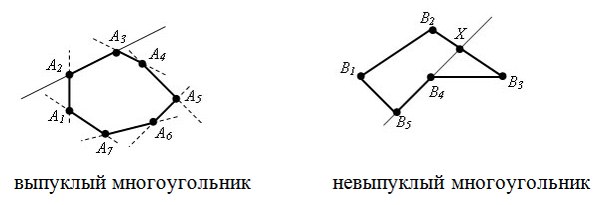
Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.
Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [Ai Ai+1, Ai+1 Ai+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.
Задача №10
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Решение
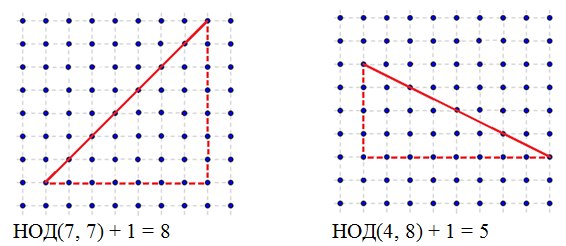
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.
Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример: 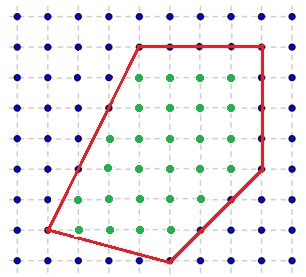
S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!
Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Векторы в C++: для начинающих
Всем привет! До этого дня мы использовали чистые массивы. Чистые — это значит простые массивы, не имеющие у себя в багаже различных функций. В этом уроке мы пройдем нечистые массивы — векторы.
Быстрый переход по статье:
Видео:Что такое вектор? | Коллинеарные векторы | Сонаправленные векторы | МегаШколаСкачать

 Что такое вектор (vector)
Что такое вектор (vector)
Вектор — это структура данных, которая уже является моделью динамического массива.
Давайте вспомним о том, что для создания динамического массива (вручную) нам нужно пользоваться конструктором new и вдобавок указателями. Но в случае с векторами всего этого делать не нужно.
Вообще, по стандарту пользоваться динамическим массивом через конструктор new — не есть правильно. Так как в компьютере могут происходить различные утечки памяти.
Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Как создать вектор (vector) в C++
Сначала для создания вектора нам понадобится подключить библиотеку — , в ней хранится шаблон вектора.
Кстати, сейчас и в будущем мы будем использовать именно шаблон вектора. Например, очередь или стек, не созданные с помощью массива или вектора, тоже являются шаблонными.
Далее, чтобы объявить вектор, нужно пользоваться конструкцией ниже:
- Вначале пишем слово vector .
- Далее в угольных скобках указываем тип, которым будем заполнять ячейки.
- И в самом конце указываем имя вектора.
В примере выше мы создали вектор строк.
Кстати, заполнить вектор можно еще при инициализации (другие способы мы пройдем позже — в методах вектора). Делается это также просто, как и в массивах. Вот так:
После имени вектора ставим знак равенства и скобки, в которых через пробел указываем значение элементов.
Такой способ инициализации можно использовать только в C++!
Так, чтобы заполнить вектор строками, нам нужно использовать кавычки — «строка» .
Второй способ обратиться к ячейке
Мы знаем, что в векторе для обращения к ячейке используются индексы. Обычно мы их используем совместно с квадратными скобками [] .
Но в C++ есть еще один способ это сделать благодаря функции — at(). В скобках мы должны указать индекс той ячейки, к которой нужно обратиться.
Вот как она работает на практике:
Давайте запустим эту программу:
Как указать количество ячеек для вектора
Указывать размер вектора можно по-разному. Можно это сделать еще при его инициализации, а можно хоть в самом конце программы. Вот, например, способ указать длину вектора на старте:
Так в круглых скобках () после имени вектора указываем первоначальную длину. А вот второй способ:
Первая строчка нам уже знакома. А вот во второй присутствует незнакомое слово — reserve , это функция, с помощью которой мы говорим компилятору, какое количество ячеек нам нужно использовать.
Вы можете задать логичный вопрос:»А в чем разница?». Давайте создадим два вектора и по-разному укажем их количество ячеек.
Как видим, в первом случае мы вывели три нуля, а во втором: 17, 0, 0.
Все потому, что при использовании первого способа все ячейки автоматически заполнились нулями.
При объявлении чего-либо (массива, вектора, переменной и т.д) мы выделяем определенное количество ячеек памяти, в которых уже хранится ненужный для ПК мусор. В нашем случае этим мусором являются числа.
Поэтому, когда мы вывели второй вектор, в нем уже находились какие-то рандомные числа — 17, 0, 0. Обычно они намного больше. Можете кстати попробовать создать переменную и вывести ее значение.
Нужно помнить! При использовании второго способа есть некоторый плюс — по времени. Так как для первого способа компилятор тратит время, чтобы заполнить все ячейки нулями.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

 Как сравнить два вектора
Как сравнить два вектора
Если в середине программы нам понадобиться сравнить два массива, мы, конечно, используем цикл for и поочередно проверим все элементы.
Вектор снова на шаг впереди! Чтобы нам сравнить два вектора, потребуется применить всего лишь оператор ветвления if.
Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Как использовать вектор (vecto) в C++
Массив — это серия объектов одного и того же типа в последовательных ячейках памяти. Массив не может увеличить длину руды. Вектор похож на массив, но его длина может быть увеличена или уменьшена. Следовательно, вектор имеет гораздо больше операций, чем массив.
C ++ имеет множество библиотек, все из которых составляют стандартную библиотеку C ++. Одна из этих библиотек — это библиотека контейнеров. Контейнер — это набор объектов, и с этой коллекцией можно выполнять определенные операции. Контейнеры C ++ можно сгруппировать в два набора: контейнеры последовательности и ассоциативные контейнеры. Контейнеры последовательности — это vector, array (не тот массив, который обсуждался ранее), deque, forward_list и list. Это разные коллекции (структуры данных, подобные массивам), и каждая предлагает различные компромиссы.
Любой программист должен знать, как решить, использовать ли вектор, массив, двухстороннюю очередь, forward_list или список. Когда программисту нужна структура, которая требует больше операций, чем те, которые связаны с обычным массивом, обычный массив использовать не следует.
Если задача включает частые вставки и удаления в середине последовательности, следует использовать список или forward_list. Если задача включает частые вставки и удаления в начале или конце последовательности, следует использовать двухстороннюю очередь. Вектор следует использовать, когда такого рода операции не требуются.
В этой статье показано, как использовать вектор C ++. Для понимания этой статьи вам потребуются некоторые знания указателей, ссылок и массивов C ++.
Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Класс и объекты
Класс — это набор переменных и функций, которые работают вместе, где переменным не присвоены значения. Когда переменным присваиваются значения, класс становится объектом. Различные значения, присвоенные одному и тому же классу, приводят к разным объектам; то есть разные объекты могут принадлежать к одному классу, но иметь разные значения. Создание объекта из класса также известно как создание экземпляра объекта.
Термин вектор описывает класс. Объект, созданный из вектора, имеет имя, выбранное программистом.
Функция, принадлежащая классу, необходима для создания экземпляра объекта из класса. В C ++ эта функция имеет то же имя, что и имя класса. Различные объекты, созданные (экземпляры) из класса, имеют разные имена, данные каждому из них программистом.
Создание объекта из класса означает создание объекта; это также означает создание экземпляра объекта.
Видео:Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

Класс Vector
Векторный класс уже определен и находится в библиотеке. Чтобы использовать векторный класс, программист должен включить векторный заголовок в файл со следующей директивой предварительной обработки:
После включения заголовка становятся доступными все векторные функции (элементы данных и функции-члены). Чтобы использовать объект счетчика для вывода данных на терминал (консоль), также должен быть включен заголовок объекта. Чтобы написать программу с вектором, как минимум должны быть включены следующие заголовки:
Видео:Что такое векторный базис? Душкин объяснитСкачать

Создание экземпляра вектора
Выше объявление массива с именем «foo» и количеством элементов «10». Это массив целых чисел. Объявление вектора аналогично. Для вектора количество элементов не является обязательным, поскольку длина вектора может увеличиваться или уменьшаться.
На этом этапе программы векторный класс уже определен в библиотеке, и заголовок включен. Вектор может быть создан следующим образом:
Здесь вектор принадлежит специальной функции-конструктору. Тип данных, которые будет содержать вектор, — это «int» в угловых скобках. Термин «vtr» — это имя, выбранное программистом для вектора. Наконец, «8» в скобках — это ориентировочное количество целых чисел, которые будет иметь вектор.
Термин «std» означает стандартное пространство имен. В этом контексте после этого термина должно стоять двойное двоеточие. Кто угодно может написать свою собственную библиотеку векторных классов и использовать ее. Однако в C ++ уже есть стандартная библиотека со стандартными именами, включая «вектор». Чтобы использовать стандартное имя, стандартному имени должен предшествовать std . Чтобы не вводить std :: каждый раз в программе для стандартного имени, файл программы может запускаться следующим образом:
Видео:Как разложить вектор по базису - bezbotvyСкачать

Перегрузка функции
Когда две или более разных сигнатур функций имеют одно и то же имя, это имя считается перегруженным. Когда вызывается одна функция, количество и тип аргументов определяют, какая функция выполняется.
Видео:vector | Библиотека стандартных шаблонов (stl) | Уроки | C++ | #1Скачать

Построение вектора
Построение вектора означает инстанцирование (создание) векторного объекта. Функция-конструктор перегружается следующим образом:
vector name
Это создает вектор нулевой длины и набирает «T.» Следующая инструкция создает вектор нулевой длины типа «float» с именем «vtr»:
vector name (n)
Это создает вектор с n элементами типа «T.» Утверждение для этого вектора с четырьмя элементами с плавающей запятой выглядит следующим образом:
vector name (n, t)
Это создает вектор из n элементов, инициализированных значением t. Следующий оператор создает вектор из 5 элементов, каждый из которых имеет значение 3,4:
Видео:➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

Конструирование с инициализацией
Вектор может быть сконструирован (создан) и инициализирован одновременно одним из следующих двух способов:
Обратите внимание, что сразу после имени объекта скобок нет. Круглые скобки, используемые сразу после имени объекта, должны содержать список инициализаторов, как показано ниже:
Вектор может быть создан и инициализирован позже с помощью списка инициализаторов. В этом случае круглые скобки использоваться не будут:
Это конструктор копирования. Он создает вектор V2 как копию вектора V1. Следующий код иллюстрирует это:
Видео:Разложение вектора по базису. 9 класс.Скачать

Назначение вектора во время Construction
Во время построения может быть создан пустой вектор, в то время как ему назначен другой, следующим образом:
Второй оператор эквивалентен:
Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

const Vector
Константный вектор — это вектор, элементы которого нельзя изменить. Значения в этом векторе доступны только для чтения. При создании вектор выглядит следующим образом:
В этом векторном типе ни один элемент не может быть добавлен или удален. Более того, никакое значение не может быть изменено.
Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Конструирование с помощью Iterator
Шаблон предоставляет общее представление для типа данных. Итератор обеспечивает общее представление сканирования значений контейнера. Синтаксис для создания вектора с итератором следующий:
template class InputIterator >
vector ( InputIterator first , InputIterator last , const Allocator & = Allocator ( ) ) ;
Это создает вектор для диапазона [первый, последний) с использованием указанного распределителя, который будет обсуждаться позже в этой статье.
Видео:Коллинеарные векторы.Скачать

Уничтожение вектора
Чтобы уничтожить вектор, просто позвольте ему выйти из области видимости, и уничтожение будет выполнено автоматически.
Видео:Единичный векторСкачать

Емкость вектора
size_type capacity () const noexcept
Общее количество элементов, которые вектор может содержать без перераспределения, возвращается функцией-членом емкости. Сегмент кода для этого выглядит следующим образом:
vector float > vtr ( 4 ) ;
int num = vtr. capacity ( ) ;
cout num ‘ n ‘ ;
reserve(n)
Пространство памяти не всегда доступно. Дополнительное место можно зарезервировать заранее. Рассмотрим следующий фрагмент кода:
vector float > vtr ( 4 ) ;
vtr. reserve ( 6 ) ;
cout vtr. capacity ( ) ‘ n ‘ ;
Результатом будет 6. Таким образом, зарезервировано дополнительное пространство 6 — 4 = 2 элемента. Функция возвращает void.
size () const noexcept
Это возвращает количество элементов в векторе. Следующий код иллюстрирует эту функцию:
vector float > vtr ( 4 ) ;
float sz = vtr. size ( ) ;
cout sz ‘ n ‘ ;
shrink_to_fit()
После предоставления дополнительной емкости вектору с помощью функции reserve () размер вектора можно уменьшить, чтобы он соответствовал его исходному размеру. Следующий код иллюстрирует это:
vector float > vtr ( 4 ) ;
vtr. reserve ( 6 ) ;
vtr. shrink_to_fit ( ) ;
int sz = vtr. size ( ) ;
cout sz ‘ n ‘ ;
На выходе будет 4, а не 6. Функция возвращает void.
resize(sz), resize(sz,c)
Это изменяет размер вектора. Если новый размер меньше старого, то элементы ближе к концу стираются. Если новый размер больше, то ближе к концу добавляется какое-то значение по умолчанию. Чтобы добавить определенную ценность, используйте функцию resize () с двумя аргументами. Следующий фрагмент кода иллюстрирует использование этих двух функций:
vector float > vtr1 ;
vtr1. resize ( 2 ) ;
cout «New size of vtr1: « vtr1. size ( ) ‘ n ‘ ;
vector float > vtr2 ;
vtr2. resize ( 4 , 8.8 ) ;
cout «vtr2: « vtr2 [ ] » « vtr2 [ 1 ] »
« vtr2 [ 2 ] » « vtr2 [ 3 ] ‘ n ‘ ;
New size of vtr1: 2
vtr2: 1.1 2.2 8.8 8.8
Функции возвращают void.
empty() const noexcept
Эта функция возвращает 1 для истины, если в векторе нет элементов, и 0 для false, если вектор пуст. Если вектор имеет 4 местоположения для определенного типа данных, например, с плавающей запятой, без какого-либо значения с плавающей запятой, то этот вектор не является пустым. Следующий код иллюстрирует это:
vector float > vtr ;
cout vtr. empty ( ) ‘ n ‘ ;
vector float > vt ( 4 ) ;
cout vt. empty ( ) ‘ n ‘ ;
vector float > v ( 4 , 3.5 ) ;
cout v. empty ( ) ‘ n ‘ ;
Доступ к элементу вектора
Вектор может быть подписан (проиндексирован) как массив. Подсчет индекса начинается с нуля.
vectorName[i]
Операция «vectorName [i]» возвращает ссылку на элемент в i- м индексе вектора. Следующий код выводит 3.3 для указанного выше вектора:
vectorName [i] const
Операция «vectorName [i] const» выполняется вместо «vectorName [i]», когда вектор является постоянным вектором. Эта операция используется в следующем коде:
const vector float > vtr ;
float fl = vtr [ 2 ] ;
cout fl ‘ n ‘ ;
Выражение возвращает постоянную ссылку на i- й элемент вектора.
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Присвоение значения с помощью нижнего индекса
Значение может быть присвоено непостоянному вектору следующим образом:
На выходе получается 8.8.
vectorName.at (i)
«VectorName.at (i)» похож на «vectorName [i]», но «vectorName.at (i)» более надежен. Следующий код показывает, как следует использовать этот вектор:
vector float > vtr ;
float fl = vtr. at ( 2 ) ;
cout fl ‘ n ‘ ;
at ( ) is a vector member function .
vectorName.at (i) const
«VectorName.at (i) const» похоже на «vectorName [i] const», но «vectorName.at (i) const» более надежен. «VectorName.at (i) const» выполняется вместо «vectorName.at (i)», когда вектор является постоянным вектором. Этот вектор используется в следующем коде:
const vector float > vtr ;
float fl = vtr. at ( 2 ) ;
cout fl ‘ n ‘ ;
at ( ) const is a vector member function .
Видео:Радиус векторСкачать

Присвоение значения с помощью функции at ()
Значение может быть присвоено непостоянному вектору с помощью функции at () следующим образом:
На выходе получается 8.8.
Видео:8 класс, 40 урок, Понятие вектораСкачать

Проблема с подпрограммами
Проблема с дополнительными сценариями (индексированием) заключается в том, что если индекс выходит за пределы допустимого диапазона, может быть возвращен ноль или может возникнуть ошибка во время выполнения.
front()
Это возвращает ссылку на первый элемент вектора без удаления элемента. Результатом следующего кода является 1.1.
Элемент не удаляется из вектора.
front() const
Когда конструкции вектора предшествует const, выражение «front () const» выполняется вместо «front ()». Это используется в следующем коде:
const vector float > vtr ;
float fl = vtr. front ( ) ;
cout fl ‘ n ‘ ;
Возвращается постоянная ссылка. Элемент не удаляется из вектора.
back()
Это возвращает ссылку на последний элемент вектора без удаления элемента. Вывод следующего кода — 4.4.
back() const
Когда конструкции вектора предшествует const, выражение «back () const» выполняется вместо «back ()». Это используется в следующем коде:
const vector float > vtr ;
float fl = vtr. back ( ) ;
cout fl ‘ n ‘ ;
Возвращается постоянная ссылка. Элемент не удаляется из вектора.
Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Доступ к векторным данным
data() noexcept; data() const noexcept;
Любой из них возвращает указатель, такой что [data (), data () + size ()) — является допустимым диапазоном.
Подробнее об этом будет рассказано позже в статье.
Возвращение итераторов и вектора
Итератор похож на указатель, но имеет больше функций, чем указатель.
begin() noexcept
Возвращает итератор, указывающий на первый элемент вектора, как в следующем сегменте кода:
vector float > vtr ;
vector float >:: iterator iter = vtr. begin ( ) ;
cout * iter ‘ n ‘ ;
На выходе получается 1.1. Обратите внимание, что объявление, которое получает итератор, было объявлено. Итератор разыменовывается в возвращаемом выражении для получения значения так же, как разыменование указателя.
begin () const noexcept;
Возвращает итератор, указывающий на первый элемент вектора. Когда конструкции вектора предшествует константа, выражение «begin () const» выполняется вместо «begin ()». При этом условии соответствующий элемент в векторе не может быть изменен. Это используется в следующем коде:
const vector float > vtr ;
vector float >:: const_iterator iter = vtr. begin ( ) ;
cout * iter ‘ n ‘ ;
На выходе получается 1.1. Обратите внимание, что на этот раз был использован «const_iterator» вместо простого «итератора» для получения возвращенного итератора.
end() noexcept
Возвращает итератор, который указывает сразу за последним элементом вектора. Рассмотрим следующий фрагмент кода:
vector float > vtr ;
vector float >:: iterator iter = vtr. end ( ) ;
cout * iter ‘ n ‘ ;
Результатом будет 0, что бессмысленно, поскольку за последним элементом нет конкретного элемента.
end() const noexcept
Возвращает итератор, который указывает сразу за последним элементом вектора. Когда конструкции вектора предшествует «const», выражение «end () const» выполняется вместо «end ()». Рассмотрим следующий фрагмент кода:
const vector float > vtr ;
vector float >:: const_iterator iter = vtr. end ( ) ;
cout * iter ‘ n ‘ ;
Результатом будет 0. Обратите внимание, что на этот раз был использован «const_iterator» вместо простого «итератора» для получения возвращенного итератора.
Обратная итерация
Возможно иметь итератор, который выполняет итерацию от конца до самого первого элемента.
rbegin() noexcept
Возвращает итератор, указывающий на последний элемент вектора, как в следующем сегменте кода:
vector float > vtr ;
vector float >:: reverse_iterator rIter = vtr. rbegin ( ) ;
cout * rIter ‘ n ‘ ;
Обратите внимание, что объявлено объявление, получающее обратный итератор. Итератор разыменовывается в возвращаемом выражении для получения значения так же, как разыменование указателя.
rbegin () const noexcept;
Возвращает итератор, указывающий на последний элемент вектора. Когда конструкции вектора предшествует «const», выражение «rbegin () const» выполняется вместо «rbegin ()». При этом условии соответствующий элемент в векторе не может быть изменен. Эта функция используется в следующем коде:
const vector float > vtr ;
vector float >:: const_reverse_iterator rIter = vtr. rbegin ( ) ;
cout * rIter ‘ n ‘ ;
Обратите внимание, что на этот раз был использован const_reverse_iterator вместо только reverse_iterator для получения возвращенного итератора.
rend () noexcept
Возвращает итератор, который указывает непосредственно перед первым элементом вектора. Рассмотрим следующий фрагмент кода:
vector float > vtr ;
vector float >:: reverse_iterator rIter = vtr. rend ( ) ;
cout * rIter ‘ n ‘ ;
Результатом будет 0, что не имеет смысла, поскольку непосредственно перед первым элементом нет конкретного элемента.
rend () const noexcept
Возвращает итератор, который указывает непосредственно перед первым элементом вектора. Когда конструкции вектора предшествует «const», выражение «rend () const» выполняется вместо «rend ()». Рассмотрим следующий фрагмент кода:
const vector float > vtr ;
vector float >:: const_reverse_iterator rIter = vtr. rend ( ) ;
cout * rIter ‘ n ‘ ;
Обратите внимание, что на этот раз был использован const_reverse_iterator вместо только reverse_iterator для получения возвращенного итератора.
Векторные модификаторы
Модификатор, изменяющий вектор, может принимать или возвращать итератор.
a.emplace (p, args)
Вставляет объект типа T, созданный с помощью std :: forward (args)… перед p.
insert(iteratorPosition, value)
Вставляет копию значения в позицию итератора вектора. Возвращает итератор (позицию) в векторе, куда была помещена копия. Следующий код показывает, где было размещено значение:
vector int > vtr ;
vector int >:: iterator iter = vtr. begin ( ) ;
++ iter ;
++ iter ;
vtr. insert ( iter , 25 ) ;
cout vtr [ 1 ] ‘ ‘ vtr [ 2 ] ‘
‘ vtr [ 3 ] ‘ n ‘ ;
Обратите внимание, что итератор был расширен (увеличен) точно так же, как указатель.
Также можно вставить список инициализаторов, как показано в следующем коде:
vector int > vtr ;
vector int >:: iterator iter = vtr. begin ( ) ;
++ iter ;
++ iter ;
vtr. insert ( iter , ) ;
cout vtr [ 1 ] ‘ ‘ vtr [ 2 ] ‘
‘ vtr [ 3 ] ‘ ‘ vtr [ 4 ] ‘ n ‘ ;
Вывод: 20 25 28 30.
erase(position)
Удаляет элемент в позиции, на которую указывает итератор, затем возвращает позицию итератора. Следующий код иллюстрирует это:
vector int > vtr ;
vector int >:: iterator iter = vtr. begin ( ) ;
++ iter ;
++ iter ;
vtr. erase ( iter ) ;
cout vtr [ ] ‘ ‘ vtr [ 1 ] ‘
‘ vtr [ 2 ] ‘ n ‘ ;
push_back(t), push_back(rv)
Используется для добавления одного элемента в конец вектора. Используйте push_back (t) следующим образом:
vector float > vtr ;
vtr. push_back ( 5.5 ) ;
float fl = vtr [ 4 ] ;
cout fl ‘ n ‘ ;
pop_back()
Удаляет последний элемент, не возвращая его. Размер вектора уменьшается на 1. Следующий код иллюстрирует это:
vector float > vtr ;
vtr. pop_back ( ) ;
float sz = vtr. size ( ) ;
cout sz ‘ n ‘ ;
a.swap(b)
Два вектора можно поменять местами, как показано в следующем фрагменте кода:
vector float > vtr1 ;
vector float > vtr2 ;
vtr1. swap ( vtr2 ) ;
cout «vtr1: « vtr1 [ ] » « vtr1 [ 1 ] »
« vtr1 [ 2 ] » « vtr1 [ 3 ] ‘ n ‘ ;
cout «vtr2: « vtr2 [ ] » « vtr2 [ 1 ] »
« vtr2 [ 2 ] » « vtr2 [ 3 ] ‘ n ‘ ;
Обратите внимание, что длина вектора при необходимости увеличивается. Кроме того, значения, для которых не было замен, заменяются некоторым значением по умолчанию.
clear()
Удаляет все элементы из вектора, как показано в следующем сегменте кода:
Операторы равенства и отношения для векторов
The == Operator
Возвращает 1 для истины, если два вектора имеют одинаковый размер и соответствующие элементы равны; в противном случае он возвращает 0 для ложного. Например:
vector int > U ;
vector int > V ;
bool bl = U == V ;
cout bl ‘ n ‘ ;
The != Operator
Возвращает 1 для истины, если два вектора не имеют одинакового размера и / или соответствующие элементы не равны; в противном случае он возвращает 0 для ложного. Например:
vector int > U ;
vector int > V ;
bool bl = U != V ;
cout bl ‘ n ‘ ;
The int > U ;
vector int > V ;
bool bl = U V ;
cout bl ‘ n ‘ ;


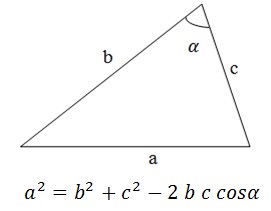
 Что такое вектор (vector)
Что такое вектор (vector) Как сравнить два вектора
Как сравнить два вектора