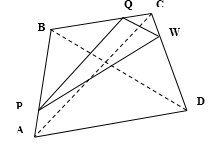
Условие
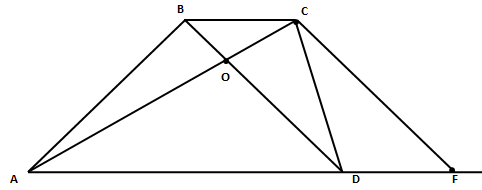
Точки P, Q, W делят стороны выпуклого четырёхугольник ABCD в отношении AP:PB=CQ:QB=CW:WD=3:4; радиус описанной окружности около треугольника PQW равен 10, PQ=16, QW=12.
а) Доказать, что треугольник PQW-прямоугольный.
б) Найти площадь ABCD.
Решение
По теореме синусов из треугольника PQW:
PQ/sin∠W=2R ⇒ sin∠W=PQ/2R=16/20=4/5;
QW/sin∠P=2R ⇒ sin∠P=QW/2R=12/20=3/5.
sin^2∠W+sin^2∠P=(4/5)^2+(3/5)^2=1
Значит, ∠W+∠P=90° и
∠Q=90°. Треугольник PQW–прямоугольный.
б) Из подобия треугольников ВСD и QCW
BD:12=7:3.
BD=28
Из подобия треугольников AВС и PBQ
AC:16=7:4
AC=28
S(ABCD)=BD•AC/2=28•28/2=392 кв. ед.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Точки p q w делят стороны выпуклого четырехугольника в отношении
Точки P, Q, W делят стороны выпуклого четырехугольника ABCD в отношении AP : PB = CQ : QB = CW : WD = 3 : 4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ — острый.
а) Докажите, что треугольник PQW — прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
а) По теореме синусов в треугольнике PQW имеем
Следовательно, откуда, учитывая, что угол W острый, находим, что
и, значит,
то есть
треугольник PQW прямоугольный.
б) Треугольники ABC и PBQ подобны с коэффициентом подобия Отсюда следует, что PQ и AC параллельны и
Аналогично QW и BD параллельны и BD = 28. Угол между прямыми AC и BD равен углу между прямыми PQ и QW. Угол между диагоналями четырёхугольника ABCD прямой. Поэтому его площадь равна
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
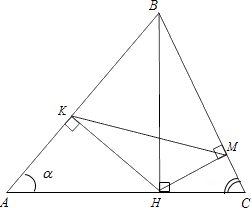
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать  16. ПланиметрияФормат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков. Примеры ответов: 7 или здесьисейчас или 3514 В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно. а) Докажите, что отрезки AM и MK равны. б) Найдите MK, если AB=5, AC=8. Пусть $angle BAC=angle BCA=alpha .$ Тогда $angle ABC=180^-2alpha .$ $angle HBA=180^-180^+2alpha =2alpha $ как смежный с $angle ABC.$ Так как треугольник $AHB$ — прямоугольный, то $angle HAB=90^-2alpha .$ $angle HAC=angle HAB+angle BAC=90^-alpha .$ Так как треугольник $AHM$ — прямоугольный, то $angle AHM=90^-90^+alpha =alpha .$ Аналогично из прямоугольго треугольника $HKB$ получаем, что $angle BHK=90^-2alpha .$ Рассмотрим $angle AHB=90^=angle AHM+angle THK+angle BHK=alpha +angle THK+90^-2alpha Rightarrow angle THK=alpha .$ В треугольниках $ATM$ и $HTK$ $angle TAM=angle THK$ по доказанному, $angle AMT=angle HKT=90^$ по условию. Значит, данные треугольники подобны по призкаку подобия по 2 углам. Следовательно, $displaystyle frac=displaystyle fracRightarrow displaystyle frac=displaystyle frac.$ В треугольнике $ATH$ и $MTK$ $angle ATH=angle MTK$ как вертикальные, $displaystyle frac=displaystyle frac$ по доказанномую Значит, данные треугольники подобны по 2 пропорциональнымсторонам и углу между ними. Тогда, $angle AHT=angle TKM=alpha .$ Получили, что в треугольнике $AKM$ углы при стороне $AK$ равны, значит, треугольник — равнобедренный и $AM=KM.$ Проведем прямую $BP//HM.$ В равнобедренном треугольнике $ABC$ отрезок $BP$ будет являться высотой и медианой, поэтому $PC=4.$ По теорем е Пифагора $BP^=sqrt<BC^-PC^>=3.$ Прямая $BP$ отсекает от треугольника $HCM$ подобные ему треугольник $BCP,$ поэтому $displaystyle frac=displaystyle frac,$ $displaystyle frac=displaystyle fracRightarrow HC=displaystyle fracCM.$ Обозначим $CM=x,$ тогда $HC=displaystyle fracx,$ $BH=displaystyle fracx-5,$ $AM=8-x.$ Из треугольника $ABH$ по теореме Пифагора $AH^=AB^-BH^=25-(displaystyle fracx-5)^=displaystyle fracx-displaystyle fracx^.$ Аналогично из треугольника $AHC$ $AC^=AH^+HC^$ $64=displaystyle fracx-displaystyle fracx^+displaystyle fracx^$ Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10. а) Докажите, что диагонали перпендикулярны. б) Найдите высоту трапеции. а) Проведем прямую CF//BD, тогда BCFD – параллелограмм и BC = DF, CF = BD. В треугольнике ACF AC = 8, CF = 6, AF = AD + DF = 10. Если диагонали перпендикулярны, то треугольник ACF – прямоугольный и выполняется теорема Пифагора: Значит, угол между диагоналями равен 90⁰. б) $S_=displaystyle fraccdot h=5h,$ , где h – длинна высоты. С другой стороны $S_=displaystyle fraccdot BDcdot ACcdot sin 90^=24$ Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции. а) Доказать, что M делит AD в отношении 2:1. б) Найдите расстояние от точки C до середины BD, если AD = 18, $AC=4sqrt.$. а) Поскольку ABCD — равнобедренная трапеция, то $MD=displaystyle frac=displaystyle frac=BC$ Тогда $AM=2BC$. Следовательно, $displaystyle frac=displaystyle frac$ Треугольник AMC прямоугольный. В нем $AM=displaystyle fracAD=12$ по доказанному в пункте а) и $AC=4sqrt$ по условию. По теореме Пифагора $CM^+AM^=AC^$ , откуда $CM=8$ . Треугольники BCO и MOD равны по катету и острому углу (BC=MD по доказанному в пункте а) , углы CBO и ADO равны как накрест лежащие). Тогда BO = OD и СO = OM как соответственные элементы равных треугольников. Значит, СO — искомое расстояние. В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно. а) Докажите, что треугольник MBK подобен треугольнику ABC. б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4. а) Обозначим $angle BAC=alpha .$. Треугольники AKH, CMH, ABH и BKH – прямоугольные. Тогда $angle KHA=angle ABH=90^-alpha .$. Аналогично $angle KHB=90^-(90^-alpha )=alpha .$. В четырехугольнике BKHM $angle BKH+angle BMH=90^+90^=180^,$, значит, вокруг этого четырехугольника можно описать окружность. Углы $angle KHB=angle KMB=alpha $ как опирающиеся на одну и ту же хорду. В треугольниках ABC и MKB $angle KMB=angle BAC,angle ABC$ — совпадающий. Значит, они подобны по признаку подобия по 2 углам. б) Обозначим k – коэффициент подобия треугольников ABC и MKB (k Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=1:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12, угол PWQ — острый. а) Докажите, что треугольник PQW — прямоугольный. б) Найдите площадь четырёхугольника ABCD. а) По теореме синусов из треугольника $PQW:$ $sin angle PWQ=displaystyle frac,sin angle QPW=displaystyle frac.$ Заметим, что $sin ^angle PWQ+sin ^angle QPW=displaystyle frac+displaystyle frac=1.$ $sin ^angle QPW=cos ^angle PWQ,$ $sin angle QPW=cos angle PWQ,$ так как угол $QWP$ — острый. Тогда $angle QPW+angle PWQ=90^$ и треугольник $PQW$ — прямоугольный. б) Треугольник $PBQ$ и $ABC$ подобные по двум стронам и углу между ими ($angle B$ — общий, $displaystyle frac=displaystyle frac=displaystyle frac).$ Значит, $ACparallel PQ$ и $AC=displaystyle fracPQ=20.$ Аналогично, из подобия треугольников $QCW$ и $BCQ$ получаем, что $BDparallel QW$ и $BD=5QN=60$ Угол между прямыми $BD$ и $AC$ равен углу между прямыми $PQ$ и $QW,$ поэтому $S_=displaystyle fracBDcdot ACcdot sin 90^=displaystyle frac60cdot 20=600.$ 🔥 ВидеоПравильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать  🔴 Через точку, делящую высоту конуса в отношении ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать  Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать  8 класс, 25 урок, Средняя линия треугольникаСкачать  Вписанные и описанные окружности. Вебинар | МатематикаСкачать  Математика, 10-й класс, Выпуклые четырёхугольники: квадрат, прямоугольник, параллелограмм, ромб...Скачать  Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать  Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать  6 (114) Длины сторон и диагоналей четырёхугольника рациональныСкачать  №165. Из точки А, удаленной от плоскости γ на расстояние d, проведены к этой плоскости наклонныеСкачать  ЕГЭ. Математика. Четырехугольники. ПрактикаСкачать  11 класс, 43 урок, Вписанный четырехугольникСкачать  №378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать  Четырехугольники, вписанные в окружность. 9 класс.Скачать  №371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать  Красивая геометрия ★ Супер ЖЕСТЬ ★ Задача для продвинутыхСкачать  №147. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника ABCD. Докажите, чтоСкачать  |