 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
2. Двугранный угол. Линейный угол двугранного угла.
3. Верно ли утверждение: если одна прямая параллельна плоскости, а другая прямая перпендикулярна этой плоскости, то прямые перпендикулярны друг другу?

4. В правильной треугольной пирамиде боковое ребро образует с плоскостью основания угол 60º. Сторона основания пирамиды равна 8 см. Найдите площадь боковой поверхности пирамиды.
Ответ: S = 48 



1. Сформулируйте определение параллельных плоскостей. Сформулируйте признак параллельности двух плоскостей.
2. Прямая призма. Сформулируйте теорему о площади боковой поверхности прямой призмы.
3. Плоскость α проходит через середины боковых сторон АВ и CD трапеции ABCD – точки M и N.
а) Докажите, что а || DA.
б) Найдите ВС, если AD=10см, NM=8см.
Видео:№129. Прямая AM перпендикулярна к плоскости квадрата ABCD, диагонали которого пересекаютсяСкачать

Плоскость, про ходящая через точки М и N, являющиеся серединами сторон будут находится на средней линии фигуры, ввиду этого образовывая прямую линию имеет свойство MN||AD||ВС; И если сия линия есть средняя линия, то сторона ВС равная Х вычисляется как (10+Х)/2=8; Х=6;
4. Дан куб ABCDA1B1C1D1. Точки К, М и Т – середины ребер СС1, В1С1 и С1D1 соответственно. Найдите АС1, если периметр сечения куба плоскостью КМТ равен 
Сечение — равносторонний треугольник.
Сторона треугольника равна половине диагонали грани.
Зная диагональ грани, найдите ребро куба.
Зная ребро куба, найдите диагональ куба. Это и есть величина АС1.
1. Угол между прямой и плоскостью.
2. Правильная пирамида. Перечислите свойства правильной пирамиды.
3. Прямая CD проходит через вершину треугольника ABC и не лежит в плоскости ABC. E и F – середины отрезков АВ и ВС.
а) Докажите, что CD и EF – скрещивающиеся прямые.
б) Найдите угол между прямыми CD и EF, если 

CD-прямая, CD не лежит в плоскости (АВС)
точка Е-середина АВ
точка F — середина ВС
а) Доказать: СD и EF — скрещивающиеся;
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

б) найти угол между CD и EF
EF – ср. линия АВС, ЕF принадлежит (АВС),
CD не лежит (АВС), СD пересекает (АВС) в точке С, значит,
СD и EF — скрещивающиеся прямые.
EF — ср. линия ABC, след-но EF||AC, а значит угол DCA = углу между CD и EF = 60⁰
4. В правильной треугольной пирамиде сторона основания равна высоте и равна 12 см. Найдите площадь поверхности пирамиды.
1. Параллелепипед и его элементы. Сделайте чертеж и пояснения.
2. Дайте определение параллельных плоскостей. Сформулируйте свойства параллельных плоскостей. Сделайте пояснения и чертежи.
Видео:№45. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма.Скачать

3. Точка М не лежит в плоскости трапеции ABCD (AB║CD).
а) Докажите, что треугольники MAD и MBC имеют параллельные средние линии.
б) Найдите длины этих средних линий, если AD:BC=5:3, а средняя линия трапеции равна 16см.
Если прямая параллельна хотя бы одной прямой лежащей в плоскости то она либо параллельная самой плоскости либо принадлежит ей.
Рассмотрим тр. AMD и BMC
A1D1 — сред. линия тр. AMD, не принадлежит ABCD, A1D1 || AD
B1C1 — сред. линия тр. BMC, не принадлежит ABCD, B1C1 || BC
по условию BC||AD ⇒ A1D1 || B1C1
KL — ср. линия трап. = 16 см
Видео:№46. Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба.Скачать

Введем переменную x ⇒ AD=5x, BC=3x
Тогда по формуле средней линии трапеции:
4. Дан куб ABCDA1B1C1D1. Диагональ АС1 равна 
Ответ: РРТH =3


1. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.
2. Сформулируйте определение скрещивающихся прямых. Сформулируйте признак скрещивающихся прямых. Сделайте чертежи и пояснения.
3. Верно ли утверждение, что все прямые, перпендикулярные к данной плоскости и пересекающие данную прямую, лежат в одной плоскости? Поясните.

Раз
Пусть Р ∈ m. Если плоскость (PMN) проходит через перпендикуляр (РМ) к другой плоскости (α), то она перпендикулярна к этой плоскости. Итак, пл. PMN ⊥ α.
Если две плоскости (PMN и α) взаимно перпендикулярны и к одной из них (к α) проведен перпендикуляр (прямая n), имеющий общую точку (N) с другой плоскостью (PMN), то этот перпендикуляр весь лежит в плоскости (PMN).
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Таким образом, любая прямая, перпендикулярная данной плоскости, лежит в плоскости PMN.
4. Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь полной и боковой поверхности призмы.
гипотенуза основания =25( теорема Пифагора, тогда площадь грани, проходящей через гипотенузу=25*h
Равновелики, значит их площади равны
1. Признак перпендикулярности прямой и плоскости.
2. Понятие многогранника. Пирамида и ее элементы. Усеченная и правильная пирамиды.
3. Через вершину А квадрата ABCD проведена прямая КА, не лежащая в плоскости квадрата.
а) Докажите, что КА и CD – скрещивающиеся прямые.
б) Найдите угол между КА и CD, если 

а) прямые AB и CD параллельны и лежат в одной плоскости, прямая KA пересекает прямую AB в точке A следовательно она не пересекает CD( так как CD не проходит через точку A) а так как они лежат в разных плоскостях то прямые KA и CD скрещивающиеся)
Видео:№23. Точка М не лежит в плоскости прямоугольника ABCD.Скачать

б)180-85-45=50 градусов угол KAB следовательно угол между прямыми KA и AB равен 50 градусам, прямые AB и CD параллельны следовательно угол между прямыми KA и CD будет равен углы между прямыми AB и CD и равен он 50 градусам.
4. Через вершину угла Е прямоугольного треугольника НРЕ с гипотенузой НЕ проведена прямая МЕ, перпендикулярная к плоскости этого треугольника. Найдите расстояние от точки М до плоскости ЕРН, если ЕР = 5 см, а расстояние от точки М до прямой РН равно 10.
💡 Видео
Параллельные прямые | Математика | TutorOnlineСкачать

№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать

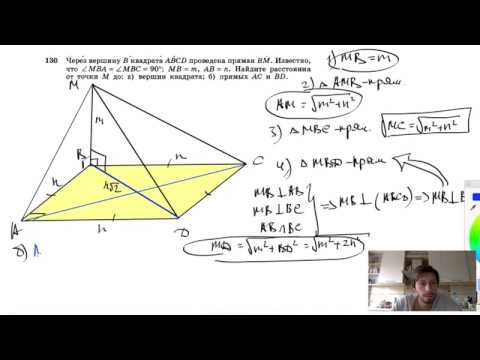
№130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВСкачать
ОГЭ математика 2024 Ященко вариант 21. Полный разбор.Скачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

Задание №152 — ГДЗ по геометрии 10 класс (Атанасян Л.С.)Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

№24. Точка М не лежит в плоскости трапеции ABCD с основанием AD.Скачать

Математика. Мастер-класс. Занятие 8. Задача С2. (13.03.15)Скачать

Консультация по решению задач по аналитической геометрии 2019-2020Скачать

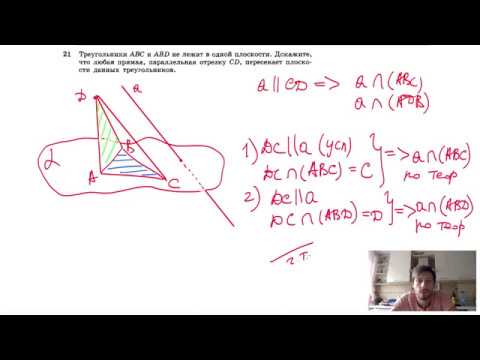
№21. Треугольники ABC и ABD не лежат в одной плоскости. Докажите,Скачать
Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

№31. Плоскость α параллельна стороне ВС треугольника ABC и проходит черезСкачать

























