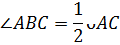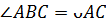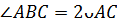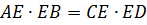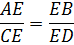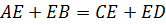Теорема о вписанном угле
Установите соответствие между вписанными углами и дугами, на которые они опираются.
Укажите соответствие для всех 3 вариантов ответа:
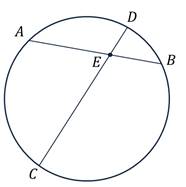
Из двух пересекающихся хорд одна разделилась на части в 25 см и 36 см, а другая — в отношении 1:4. Найдите длину второй хорды.
Выберите один из 4 вариантов ответа:
Выберите верные утверждения.
Выберите несколько из 4 вариантов ответа:
1) Вписанный угол, опирающийся на полуокружность — развёрнутый.
2) Вписанные углы равны, если они опираются на одну и ту же дугу.
3) Вписанный угол, опирающийся на полуокружность — прямой.
4) Вписанные углы равны, если их вершины совпадают.
Укажите, какие условия должны выполняться, чтобы угол был вписанным по определению.
Выберите несколько из 6 вариантов ответа:
1) стороны пересекают окружность
2) вершина лежит внутри окружности
3) вершина лежит вне окружности
4) стороны касаются окружности
5) вершина лежит на окружности
6) вершина лежит в центре окружности
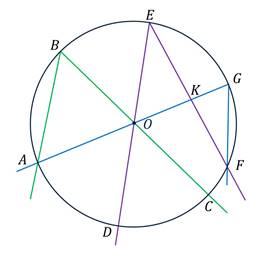
Укажите вписанные углы.
Выберите несколько из 6 вариантов ответа:
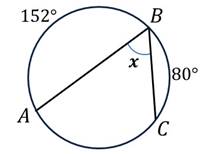
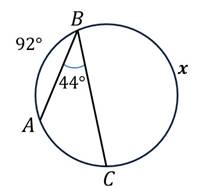
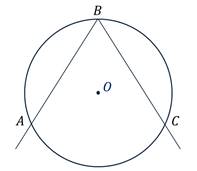
Пользуясь данными рисунка, найдите градусную меру дуги BC . В ответе укажите только количество градусов, например, 80.
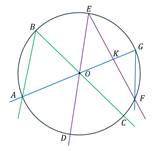
Пользуясь данными рисунка, найдите величину x вписанного угла ABC. В ответе укажите только количество градусов, например, 80.
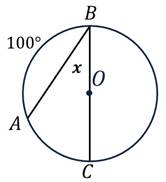
Пользуясь данными рисунка, найдите величину x вписанного угла ABC . В ответе укажите только количество градусов, например, 80.
Укажите формулу, выражающую связь величины вписанного угла с градусной мерой дуги, на которую он опирается.
1)
2)
3)
Укажите формулу, связывающую отрезки двух пересекающихся хорд.
Выберите один из 3 вариантов ответа:
1)
2)
3)
Видео:ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать

Углы, связанные с окружностью
 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Геометрия Докажите, что если вписанный угол является прямым, то он опирается на диаметрСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Центральные и вписанные углыСкачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:Центральный и вписанный углыСкачать  Прямая линия. Признаки параллельности прямых линий.Если две произвольные прямые AB и СD пересечены третьей прямой MN, то образовавшиеся при этом углы получают попарно такие названия: соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7; внутренние накрест лежащие углы: 3 и 5, 4 и 6; внешние накрест лежащие углы: 1 и 7, 2 и 8; внутренние односторонние углы: 3 и 6, 4 и 5; внешние односторонние углы: 1 и 8, 2 и 7. Описанные углы видны на рисунке: Теорема. Если две параллельные прямые пересечены третьей прямой, то сформировавшиеся: 1. внутренние накрест лежащие углы одинаковы; 2. внешние накрест лежащие углы одинаковы; 3. соответственные углы одинаковы; 4. сумма внутренних односторонних углов будет 2d = 180 0 ; 5. сумма внешних односторонних углов будет 2d = 180 0 ; Данную теорему иллюстрирует рисунок: Имеются две параллельные прямые AB и СD, их пересекает третья прямая MN. 1. ∠ 4 = ∠ 6 и ∠ 3 = ∠ 5; 2. ∠ 2 = ∠ 8 и ∠ 1 = ∠ 7; 3. ∠ 2 =∠ 6, ∠ 1 = ∠ 5, ∠ 3 = ∠ 7, ∠ 4 = ∠ 8; 4. ∠ 3 + ∠ 6 = 2d и ∠ 4 + ∠ 5 = 2d; 5. ∠ 2 + ∠ 7 = 2d и ∠ 1 + ∠ 8 = 2d. 1. Из середины E того отрезка прямой MN, который размещается между параллельными прямыми, прочертим на СD перпендикуляр EK и продолжим его до пересечения с AB в точке L. Так как перпендикуляр к одной из параллельных есть также и перпендикуляр к другой параллельной, то образовавшиеся при этом треугольники (заштрихованные на чертеже) — оба прямоугольные. Они одинаковы, потому что в них по равной гипотенузе и по одинаковому острому углу при точке E. Из равенства треугольников получаем, что внутренние накрест лежащие углы 4 и 6 одинаковы. Два прочих внутренних накрест лежащих угла 3 и 5 одинаковы, как дополнения до 2d к одинаковым углам 4 и 6 (как смежные с 4 и 6). 2. Внешние накрест лежащие углы равны соответственно внутренним накрест лежащим углам, как углы вертикальные. Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6. Следовательно, ∠ 2 =∠ 8. 3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов. 4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d. 5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам, как углы вертикальные. Из выше доказанного обоснования получаем обратные теоремы. Когда при пересечении двух прямых произвольной третьей прямой получим, что: 1. Внутренние накрест лежащие углы одинаковы; или 2. Внешние накрест лежащие углы одинаковые; или 3. Соответственные углы одинаковые; или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ; или 5. Сумма внешних односторонних равна 2d = 180 0 , 🔍 Видео7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать  Геометрия. 8 класс. Урок 11 "Вписанные углы"Скачать  Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать  11 класс, 40 урок, Угол между касательной и хордойСкачать  8 класс, 34 урок, Теорема о вписанном углеСкачать  Центральные и вписанные углы. Геометрия 8клСкачать  Геометрия 7 класс. Углы с соответственно параллельными или перпендикулярнымСкачать  №1018. Угол между лучом ОА, пересекающим единичную полуокружность, и положительной полуосью ОхСкачать  Центральные и вписанные углы.Скачать  Угол между прямыми в пространстве. 10 класс.Скачать  ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать  Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать  Точка, прямая и отрезок. 1 часть. 7 класс.Скачать  Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать  |