11 при параллельном проецировании отношение величин отрезков лежащих на прямой и их проекций (7 видео)

Методы проецирования: центральное и параллельное проецирование

Изображение объектов трехмерного пространства на плоскости получают методом проецирования.

Проецирование— это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости.

Аппарат проецирования включает в себя изображаемые объекты — точки А, В, проецирующие лучи i и плоскость проекций П’, на которой получается изображение объектов в соответствии с рисунком 1.2.

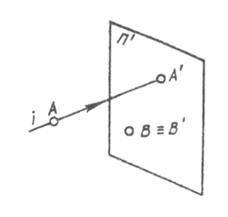11 при параллельном проецировании отношение величин отрезков лежащих на прямой и их проекций

Рисунок 1.2

Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до встречи с плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций и определяет проекцию этой точки. Так, проекцией точки А является точка А’, т. е. [i

A; i ^ П’ = А’]. Проекцией точки В является точка В’, хотя проекция точки В, лежащей в плоскости п’, совпала с самой точкой. Чтобы получить проекцию какой-либо фигуры, необходимо построить проекции ее характерных точек и соединить их на чертеже соответствующими линиями.

Построить проекции предметов на чертеже можно двумя способами: центральным и параллельным.

Наименование способа проецирования	Сущность способа
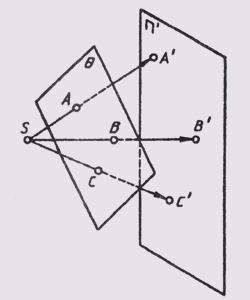
Центральное проецирование	Все лучи, проецирующие предмет, исходят из одной точки Р, называемой центром проекций (рисунок 1.3). Полученные проекции А’, В’, С’ называются центральными проекциями точек А, В, С.
Параллельное проецирование	Все проецирующие лучи проходят параллельно наперед заданному направлению S, а значит и друг другу (рисунок 1.4). Это можно уподобить случаю центрального способа проецирования, когда центр проекций S удален в бесконечность и все проецирующие лучи становятся параллельными. При построении проекций А’, В’, С’ этим способом они называются параллельными проекциями точек А, В, С.

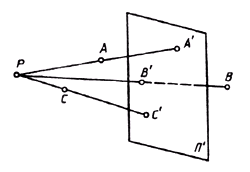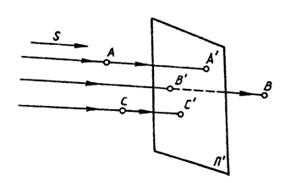Рисунок 1.3	Рисунок 1.4

Свойства проецирования

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств:

1) Проекция точки есть точка. При заданном центре Р (или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п’ единственная точка А’. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой в соответствии с рисунком 1.2.

2) Проекция прямой есть прямая. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рисунок 1.5). Если в пространстве прямая параллельна плоскости проекции П’, то ее проекция параллельна самой прямой (рисунок 1.6). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им. При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рисунок 1.7).


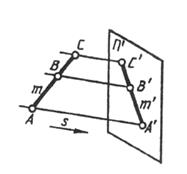Рисунок 1.6	Рисунок 1.7

3) Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а их точки пересечения с плоскостью проекций П’ — всю плоскость проекций.
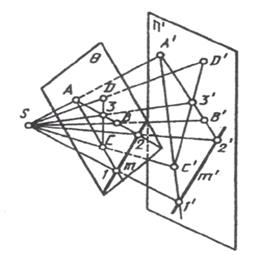	Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рисунок 1.8) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций П’, которое позволяет определить проекции (любой точки D или прямой этой плоскости).
Рисунок 1.8

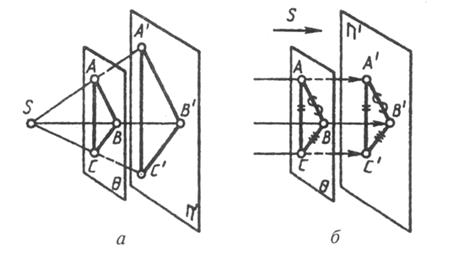
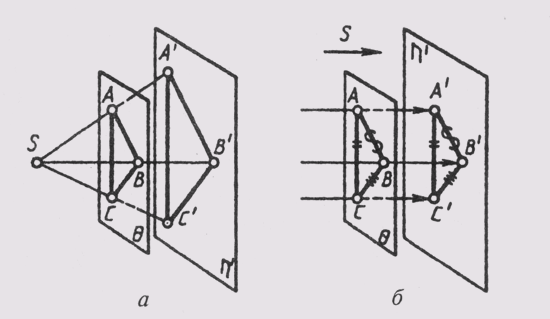
Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рисунок 1.9, а), а при параллельном — равны им (рисунок 1.9, б).

1.5 Инварианты параллельного проецирования (прямоугольное проецирование)

Ортогональное (прямоугольное) проецирование есть частный случай проецирования параллельного, когда все проецирующие лучи перпендикулярны плоскости проекций. Ортогональным проекциям присущи все свойства параллельных проекций, но при прямоугольном проецировании проекция отрезка, если он не параллелен плоскости проекций, всегда меньше самого отрезка (рисунок 1.10). Объясняется тем, что сам отрезок в пространстве является гипотенузой прямоугольного треугольника, а его проекция — катетом: А’В’ = AB cos a..

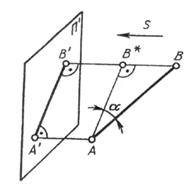Рисунок 1.10

При прямоугольном проецировании прямой угол проецируется в натуральную величину, когда обе стороны его параллельны плоскости проекций, и тогда, когда лишь одна из его сторон параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости проекций.

Теорема о проецировании прямого угла.Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой же угол.

Пусть дан прямой угол ABC, у которого сторона АВ параллельна плоскости П’ (рисунок 1.11). Проецирующая плоскость перпендикулярна плоскости П’. Значит, АВ _|_S, так как АВ _|_ ВС и АВ _|_ ВВ, отсюда АВ _|_ В’С’. Но так как АВ || А’В’ _|_ В’С’, т. е. на плоскости П’ угол между А’В’ и В’С равен 90°.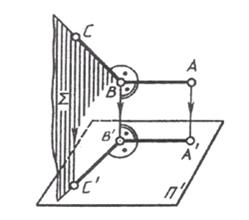

Рисунок 1.11

Обратимость чертежа.Проецирование на одну плоскость проекций дает изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А (рисунок 1.8) не определяет положение самой точки в пространстве, так как не известно, на какое расстояние она удалена от плоскости проекций п’. Любая точка проецирующего луча, проходящего через точку А, будет иметь своей проекцией точку А’. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображение дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа. В данном курсе будут рассмотрены чертежи, получаемые ортогональным проецированием на две или более взаимно перпендикулярные плоскости проекций (комплексные чертежи) и путем перепроецирования вспомогательной проекции предмета на основную аксонометрическую плоскость проекций (аксонометрические чертежи).


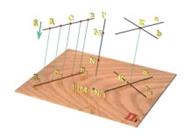Рисунок 1.12
Внимание, вопрос!	Подумайте, проанализируйте предложенные чертежи и докажите справедливость перечисленных инвариантов центрального и параллельного проецирования (рисунок 1.12).
Запомните!	1 Рассмотренные свойства (инварианты) параллельного проецирования сохраняются при любом направлении проецирования. 2 Метрические характеристики геометрических фигур при параллельном проецировании в общем случае не сохраняются (происходит искажение линейных и угловых величин).

Контрольные вопросы

1 Какие геометрические элементы включают в себя аппарат проецирования?

2 Какие способы проецирования вы знаете?

3 Какие проецирующие поверхности могут создавать проецирующие лучи?

4 Перечислите основные свойства проекций.

5 Чему равна проекция угла, плоскость которого параллельна плоскости проекций при центральном проецировании?

6 В какие геометрические образы вырождаются проекции прямых и плоскостей поверхностей, занимающих проецирующее положение?

7 Как читается теорема о проецировании прямого угла?

8 Как вы понимаете термин «обратимый чертеж? Чем достигается обратимость чертежа?
ЛЕКЦИЯ №2

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Проекции параллельных прямых

Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 5). Доказательство: прямые АВ и CD проецируются с помощью проецирующих плоскостей У и Т, но У¦Т, т. к. АВ¦CD по условию и ААN¦ССN — по построению. Известно, что если две параллельные плоскости пересекаются третьей, то образуются параллельные прямые. Здесь две параллельные плоскости У и Т пересекаются плоскостью проекций ПN и образуются параллельные прямые (АNВN¦CNDN).

Проекции геометрических фигур, параллельных плоскости проекций. Если данная геометрическая фигура — прямая, кривая линия или плоская фигура (треугольник, многоугольник, эллипс, окружность и т. п.) лежит в плоскости, параллельной плоскости проекций, то она проецируется на плоскость проекций в натуральную величину. Доказательство: дано У¦ПN и АВ У (рис. 6). Требуется доказать, что АВ¦АNВN и АВ=АNВN. Так как У¦ПN , то отрезки ААN и ВВN равны и параллельны. Следовательно, четырехугольник АВВNАN является параллелограммом и АВ¦АNВN, АВ=АNВN.

Так же доказывается теорема относительно любой плоской кривой и любой плоской фигуры.

— цилиндрические поверхности в параллельной системе проецирования и конические поверхности в центральной системе проецирования — проецируют пространственные кривые линии и пространственные фигуры.

Основное свойство проецирующей геометрической фигуры заключается в том, что точки, прямые или кривые линии, плоские и пространственные фигуры, расположенные на проецирующей геометрической фигуре, проецируются на линию пересечения этой фигуры с плоскостью проекций. Эта линия называется следом данной проецирующей геометрической фигуры или ее главной проекцией.

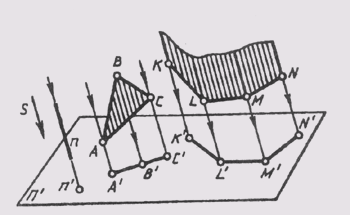
На рис. 7 показаны проецирующие геометрические фигуры в ортогональной системе проецирования: проецирующая прямая а, проецирующая плоскость У и проецирующая цилиндрическая поверхность Ф.

Прямая а, плоскость У и образующие цилиндрической поверхности Ф перпендикулярны плоскости проекций ПN . Их главные проекции аN , УN и ФN включают в себя проекции всех точек данной проецирующей геометрической фигуры.

Дополнения однокартинного чертежа. Ранее было показано, что одна проекция точки не определяет ее положения в пространстве.

Для того, чтобы чертеж был полным и обратимым, т.е. для того, чтобы по чертежу можно было представить положение точки в пространстве, применяются разные способы.

Способ числовых отметок. Около проекции точки ставится число, выражающее в некоторых линейных единицах расстояние данной точки от плоскости проекций.

На рис. 8 даны проекции различных геометрических фигур с числовыми отметками.

Около проекции точки А стоит цифра 20. Это означает, что точка А отстоит от плоскости проекций на расстоянии 20 линейных единиц.

Концы отрезка ВС отстоят от плоскости на расстояниях 15 и 30, вершины треугольника DEF — на расстояниях соответственно 0, 10 и 25.

Кривая поверхность задана кривыми линиями, принадлежащими поверхности и параллельными плоскости проекций (горизонталями, если плоскость ПN горизонтальна). Около каждой горизонтали стоит число, выражающее ее расстояние от плоскости ПN.

С помощью горизонталей изображается рельеф земной поверхности на топографических картах и сложные кривые поверхности, в том числе поверхности манекена и обувной колодки.

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.

Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п’ единственная точка А’. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).

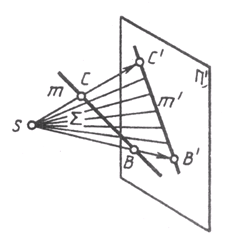
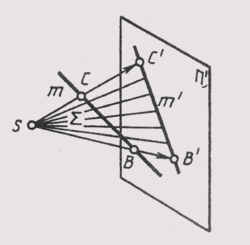
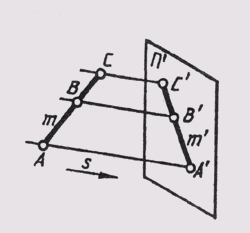
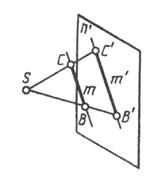
Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п’ по линии m’, являющейся проекцией на плоскость n’; S

т; S п п = т’. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 9). Если в пространстве прямая параллельна плоскости проекции п’, то ее проекция параллельна самой прямой (рис. 10). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.

При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 11):

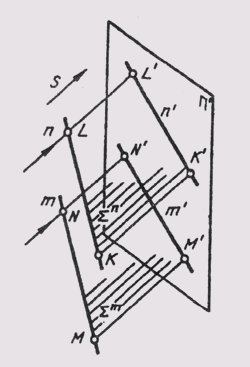
При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 12). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости Sm и Sn тоже будут параллельны. При пересечении их с плоскостью проекций п’ получаем т’|| п’.

Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а их точки пересечения с плоскостью проекций п’ — всю плоскость проекций.

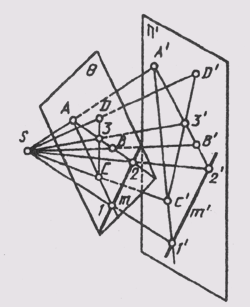
Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 13, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n’, которое позволяет определить проекции (рис. 13, б) любой точки D или прямой этой плоскости.

Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 14, а), а при параллельном — равны им (рис. 14,6).

Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA’B’C’, так как АВС бесконечность А’В’С’, а на рис. 54, б угол ABC = углу А’В’С’, так как АВС = А’В’С’.

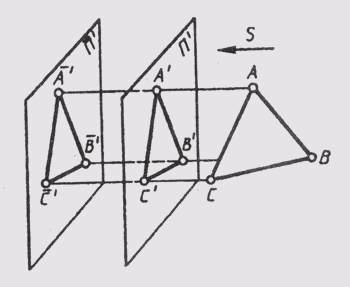
При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 15).

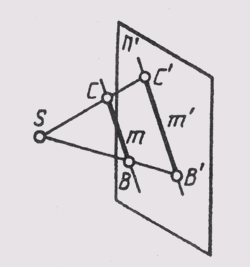
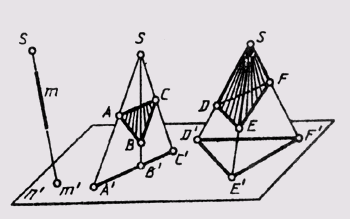
Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи. При центральном проецировании это прямые и плоскости, проходящие через центр проекций, пирамидальные и конические поверхности, у которых вершины совпадают с центром проецирования (рис. 56). При параллельном проецировании — это прямые и плоскости, параллельные направлению проецирования, призматические и цилиндрические поверхности, ребра и образующие которых параллельны направлению проецирования (рис. 57).

Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).

Видео:Лекция 1. Методы проецированияСкачать

28. Свойства проекций

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.

Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п’ единственная точка А’. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).

Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п’ по линии m’, являющейся проекцией на плоскость n’; S

т; S п п = т’. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 49). Если в пространстве прямая параллельна плоскости проекции п’, то ее проекция параллельна самой прямой (рис. 50). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.

При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 51):

При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 52). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости S m и S n тоже будут параллельны. При пересечении их с плоскостью проекций п’ получаем т’|| п’.

Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а

их точки пересечения с плоскостью проекций п’ — всю плоскость проекций.

Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 53, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n’, которое позволяет определить проекции (рис. 53, б) любой точки D или прямой этой плоскости.

Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 54, а), а при параллельном — равны им (рис. 54,6).

Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA’B’C’, так как АВС бесконечность А’В’С’, а на рис. 54, б угол ABC = углу А’В’С’, так как АВС = А’В’С’.

При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 55).