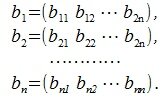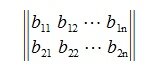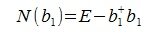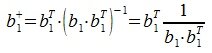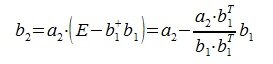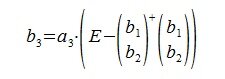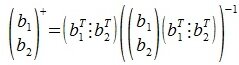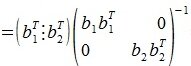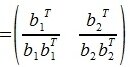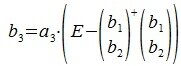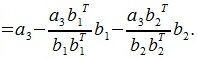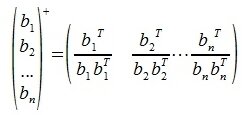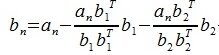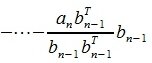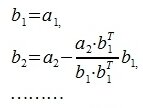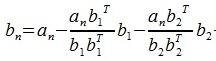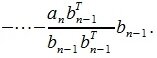Ортогонализация по шмидту векторов (3 видео)

Ортогональная матрица. Ортогонализация Грамма-Шмидта.

Квадратная матрица i=1,2. n, j=1,2. n называется ортогональной, если выполняется условие

где E — единичная матрица, A T — транспонированная матрица.

Из условия AA T =E следует, что A T является обратной к матрице A:

Для любой невырожденной квадратной матрицы можно построить ортогональную матрицу. Для построения ортогональной матрицы применяют метод ортогонализации Грамма-Шмидта. Затем нормируют полученные векторы строки. Эти две процедуры вместе называют методом ортонормализации Грамма-Шмидта.

Содержание

Ортогонализация Грамма-Шмидта
Ортонормализация Грамма-Шмидта
Ортогональные векторы евклидова пространства и их свойства
Свойства ортогональных векторов
Процесс ортогонализации Грама-Шмидта
Процесс ортогонализации Грама-Шмидта
Примеры решения задач
📺 Видео

Видео:Процесс ортогонализации Грама-Шмидта. ПримерСкачать

Ортогонализация Грамма-Шмидта

Пусть задана некоторая квадратная матрица, строки которой являются векторы

и пусть эти векторы линейно независимы (т.е. матрица построенная этими векторами строками невырождена). Требуется получить взаимно ортогональные n векторы

Суть метода заключается в следующем:

1. Выбирается некоторая строка (пусть это будет a₁). b₁ выбирается равным a₁.

3. Вектор b₃ получается проектированием a₃ на нуль-пространство матрицы

Рассмотрим подробнее процесс ортогонализации.

На втором шаге вычисляем нуль-пространство b₁:

где E- единичная матрица порядка nxn,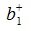-псевдообратная к b₁. Так как b₁ является вектором-строкой (матрицей-строкой), то

Для пректирования a 2 на нуль-пространство b 1 вычисляем

На третьем шаге вычисляем b 3:

Так как векторы b 1 и b 2 ортогональны, то

Для n -го вектора получим:

Таким образом, процедура ортогонализации Грамма-Шмидта имеет следующий вид:

Видео:A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

Ортонормализация Грамма-Шмидта

Суть метода ортонормализации Грамма-Шмидта заключается в ортогонализации методом Грамма-Шмидта а затем нормализации полученных векторов строк:

Видео:Лекция 5.7. Ортогонализация Грама-Шмидта: примерСкачать

Ортогональные векторы евклидова пространства и их свойства

Два вектора [math]mathbf[/math] и [math]mathbf[/math] евклидова пространства называются ортогональными (перпендикулярными) , если их скалярное произведение равно нулю: [math]langle mathbf,mathbfrangle[/math] .

Система векторов [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] называется ортогональной, если все ее векторы попарно ортогональны, т.е. [math]langle mathbf_i, mathbf_jrangle=0[/math] при [math]ine j[/math] . Система векторов [math]mathbf_1, mathbf_2, ldots,mathbf_k[/math] называется ортонормированной , если все ее векторы попарно Ортогональны и длина (норма) каждого вектора системы равна единице, т.е.

Говорят, что вектор [math]mathbf[/math] ортогонален (перпендикулярен) множеству [math]M[/math] , если он ортогонален каждому вектору из [math]M[/math] . Ортогональность векторов обозначается знаком перпендикуляра [math](perp)[/math] .

Видео:Практика 19 Процесс ортогонализации Грама ШмидтаСкачать

Свойства ортогональных векторов

1. Нулевой вектор ортогонален каждому вектору пространства.

2. Взаимно ортогональные ненулевые векторы линейно независимы.

В самом деле, пусть векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] попарно ортогональны. Составим из них линейную комбинацию и приравняем ее нулевому вектору:

Умножим обе части равенства скалярно на вектор [math]mathbf_1:[/math]

Следовательно, [math]lambda_1cdot|mathbf_1|^2=0[/math] . Так как [math]mathbf_1ne mathbf[/math] , то [math]lambda_1=o[/math] . Аналогично доказываем, что [math]lambda_2=ldots= lambda_k=0[/math] , т.е рассматриваемая линейная комбинация тривиальная. Значит, ортогональная система векторов [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] линейно независима.

3. Если сумма взаимно ортогональных векторов равна нулевому вектору, то каждое из слагаемых равно нулевому вектору.

4. Если вектор [math]mathbf[/math] ортогонален каждому вектору системы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , то он также ортогонален и любой их линейной комбинации. Другими словами, если [math]mathbfperp mathbf_i,

i=1,ldots,k[/math] , то [math]mathbfperp operatorname (mathbf_1,ldots, mathbf_k)[/math] .

5. Если вектор [math]mathbf[/math] ортогонален подмножеству [math]M[/math] евклидова пространства, то он ортогонален и линейной оболочке этого подмножества, т.e. [math]mathbfperp M

6. Если [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] — ортогональная система векторов, то

Это утверждение является обобщением теоремы Пифагора.

Видео:Ортогональные системы векторов. Процесс ортогонализации (задача 1357)Скачать

Процесс ортогонализации Грама-Шмидта

Рассмотрим следующую задачу. Дана линейно независимая система [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] векторов конечномерного евклидова пространства. Требуется построить ортогональную систему [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов того же пространства так, чтобы совпадали линейные оболочки:

Решение задачи находится при помощи процесса ортогонализации Грама–Шмидта , выполняемого за [math]k[/math] шагов.

1. Положить [math]mathbf_1=mathbf_1[/math] .

2. Найти [math]mathbf_2=mathbf_2-alpha_cdot mathbf_1[/math] , где [math]alpha_= frac<langle mathbf_2, mathbf_1rangle><langle mathbf_1, mathbf_1 rangle>[/math] .

3. Найти [math]mathbf_3=mathbf_3-alpha_ mathbf_1-alpha_ mathbf_2[/math] , где [math]alpha_=frac<langle mathbf_3,mathbf_1 rangle><langle mathbf_1, mathbf_1rangle>,

4. Найти [math]mathbf_k=mathbf_k-sum_^alpha_mathbf_i[/math] , где [math]alpha_= frac<langle mathbf_k,mathbf_irangle><langle mathbf_i, mathbf_irangle>,

Поясним процесс ортогонализации. Искомый на втором шаге вектор [math]mathbf_2[/math] представлен в виде линейной комбинации [math]mathbf_2=mathbf_2-alpha mathbf_1[/math] . Коэффициент [math]alpha[/math] подберем так, чтобы обеспечить ортогональность векторов [math]mathbf_2[/math] и [math]mathbf_1[/math] . Приравняем нулю скалярное произведение этих векторов [math]langle mathbf_2,mathbf_1rangle= langle mathbf_2,mathbf_1rangle- alpha langle mathbf_1,mathbf_1rangle=0[/math] . Отсюда получаем, что [math]alpha=alpha_[/math] (см. пункт 2 алгоритма). Подбор коэффициентов [math]alpha_[/math] на j-м шаге алгоритма делается так, чтобы искомый вектор [math]mathbf_j[/math] был ортогонален всем ранее найденным векторам [math]mathbf_1, mathbf_2,ldots,mathbf_[/math] .

1. Векторы, найденные в процессе ортогонализации, обладают следующими свойствами:

а) [math]mathbf_j perp operatorname(mathbf_1,mathbf_2,ldots,mathbf_),quad j=2,ldots,k[/math] ;

б) [math]operatorname(mathbf_1)= operatorname(mathbf_1),quad operatorname(mathbf_1,mathbf_2, ldots,mathbf_)= operatorname(mathbf_1,mathbf_2, ldots,mathbf_),quad j=2,ldots,k[/math] .

Первое свойство следует из свойства 4 ортогональных векторов. Второе свойство следует из того, что каждый вектор системы [math]mathbf_1,mathbf_2,ldots,mathbf_[/math] линейно выражается через векторы [math]mathbf_1,mathbf_2, ldots, mathbf_[/math] , и наоборот.

2. В процессе ортогонализации любой вектор [math]mathbf_j[/math] можно заменить на коллинеарный ему ненулевой вектор [math]lambdacdot mathbf_j[/math] . При этом свойства, перечисленные в пункте 1, не нарушаются.

3. Если система [math]mathbf_1,mathbf_2,ldots, mathbf_[/math] векторов линейно зависима, то в процессе ортогонализации будем получать (на некоторых шагах) нулевые векторы. Действительно, если подсистема math]mathbf_1,mathbf_2,ldots, mathbf_[/math] линейно зависима, то [math]mathbf_jin operatorname (mathbf_1,ldots,mathbf_)[/math] . Тогда вектор [math]mathbf_j=mathbf_j-sum_^alpha_ mathbf_i[/math] одновременно удовлетворяет двум условиям [math]mathbf_jperp operatorname(mathbf_1,ldots, mathbf_)[/math] и [math]mathbf_jin operatorname(mathbf_1,ldots,mathbf_)[/math] . Значит, это нулевой вектор [math]mathbf_i=mathbf[/math] .

Поэтому в данном случае формулы вычисления коэффициентов [math]alpha_[/math] на j-м шаге следует записывать в виде:

В остальном процесс ортогонализации остается неизменным.

4. Процесс ортогонализации можно дополнить процессом нормировки, разделив каждый вектор ортогональной системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] на его длину:

В результате получим ортонормированную систему [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , отвечающую условию [math]operatorname(mathbf_1, ldots, mathbf_k)= operatorname(mathbf_1,ldots,mathbf_k)[/math] . Если исходная система векторов является линейно зависимой, то среди векторов ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] будут нулевые. Чтобы получить ортонормированную систему, нулевые векторы следует исключить, а остальные векторы нормировать.

Пример 8.18. Даны системы векторов евклидовых пространств:

а) [math]x=begin1\0end!,quad y=begin2\0end!,quad z=begin0\1end[/math] — элементы пространства [math]mathbb^2[/math] со скалярным произведением (8.26):

p_3(x)=x^2[/math] — элементы пространства [math]C[-1;1][/math] со скалярным произведением (8.28):

Провести ортогонализацию данных векторов.

Решение. а) Заметим, что система векторов [math]x,,y,,z[/math] линейно зависимая, так как [math]x[/math] и [math]y[/math] пропорциональны, поэтому используем процесс ортогонализации Грама–Шмидта с учетом пункта 3 замечаний 8.11.

1. Полагаем [math]mathbf=x[/math] .

Проверим условие ортогональности [math]langle mathbf,mathbfrangle= 2cdot1cdot left(-fracright)+ 1cdot1+ 0cdotleft(-fracright)+0cdot1=0[/math] .

Для получения ортонормированной системы исключаем нулевой вектор [math]mathbf=mathbf[/math] , а остальные нормируем (см. пункт 4 замечаний 8.11):

Таким образом, для системы трех векторов [math]x,,y,,z[/math] построена ортогональная система из трех векторов [math]mathbf,mathbf,mathbf[/math] и ортонормированная система из двух векторов [math]widehat<mathbf>,widehat<mathbf>[/math] . Линейные оболочки этих трех систем совпадают между собой (и со всем пространством [math]mathbb^2[/math] ).

б) 1. Полагаем [math]q_1(x)=p_1(x)=1[/math] .

и находим [math]q_3(x)= x^2-alpha_cdot1-alpha_cdot x=x^2-frac[/math] .

Получили ортогональные многочлены [math]q_1(x)=1,

q_3(x)=x^2-frac[/math] . Выполним нормировку:

Видео:Процесс ортогонализации Грама-Шмидта. ТемаСкачать

Процесс ортогонализации Грама-Шмидта

Определение. Векторы $a$ и $b$ называются ортогональными, если их скалярное произведение равно нулю.$$left(a, bright)=0.$$

Определение. Системы $S_ = langle a_,a_,…,a_rangle,$ и $S_ = langle b_,b_,…,b_rangle,$ называются эквивалентными, когда векторы каждой из систем, линейно выражаются через векторы, другой системы.

Теорема. Допустим, у нас есть линейно независимая система $S = langle a_,a_,ldots,a_rangle.$ Тогда всегда найдется такая система $S_ = langle b_,b_,…,b_rangle,$ которая будет эквивалентной и ортогональной к $S,$ которая получается следующим методом:

Докажем же существование $S_$ эквивалентной $S$ с помощью индукции. При $k = 1$ $$b_ = a_.$$ При $k = 2$ $$left(b_, b_right) = left(a_ + lambda_b_, b_right) = left(a_, b_right) + lambda_left(b_, b_right) =$$$$= left(a_, b_right)-dfrac<left(a_, b_right)><left(b_, b_right)>left(b_, b_right) = 0.$$ Из чего очевидно, что $S = langle a_,a_rangle$ и $S_ = langle b_,b_rangle$ — эквивалентны.

Теперь докажем для $k = m,$ при $2leqslant jleqslant k$ $$left(b_, b_right) = left(a_ + sumlimits_^lambda_b_, b_right) = left(a_, b_right) + sumlimits_^lambda_left(b_, b_right) =$$$$= left(a_, b_right)-sumlimits_^dfrac<left(a_, b_right)><left(b_, b_right)>left(b_, b_right) = 0.$$ Как видим, по индукции мы доказали, что любой ЛНЗ системе, методом Грама-Шмидта, можно найти эквивалентную ей ортогональную систему.

Видео:Лекция 5.8. Ортогонализация Грама-ШмидтаСкачать

Примеры решения задач

Рассмотрим примеры задач, в которых может использоваться процесс ортогонализации Грама-Шмидта. Постарайтесь решить данные примеры самостоятельно, а затем сверить свое решение с приведенным.

Применяя процесс ортогонализации по Грамму-Шмидту построить ортогональный базис подпространства, натянутого на данную систему векторов $S = langle a_, a_, a_rangle.$
$$a_ = (1, 2, 2, -1), a_ = (1, 1, -5, 3), a_ = (3, 2, 8, -7).$$

Первым делом, найдем $b_$. В первом пункте пишется, что $b_ = a_.$

Дальше найдем $b_.$ Из формулы пункта 2), мы видим, что: $$b_ = a_ + lambda_ cdot b_, lambda_ = dfrac<left(a_, b_right)><left(b_, b_right)>,$$ все необходимое для решения мы нашли, осталось только решить. Итак:$$lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)> = -dfrac = -left(dfracright) = 1,$$ лямбду мы нашли, $b_$ у нас есть, теперь мы можем найти $b_:$ $$b_ = a_ + lambda_cdot b_ = (1, 1, -5, 3) + (1, 2, 2, -1) = (2, 3, -3, 2).$$

Выпишем же формулу для $b_:$ $$b_ = a_ + lambda_ cdot b_ + lambda_ cdot b_,$$ при $$lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)>,quad lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)>,$$ найдем все необходимое: $$lambda_ = -dfrac= -3,$$ $$lambda_ = -dfrac= 1.$$ Теперь вычислим $b_:$ $$b_ = (3, 2, 8, -7)-3(1, 2, 2, -1) + 1(2, 3, -3, 2) = (2, -1, -1, 2).$$
Получили ортогональный базис $S_ = langle b_, b_, b_rangle$ — систему, эквивалентную данной, $S = langle a_, a_, a_rangle.$ $$S_ = langle (1, 2, 2, -1), (2, 3, -3, 2), (2, -1, -1, 2)rangle.$$

Применяя процесс ортогонализации по Грамму-Шмидту построить ортогональный базис подпространства, натянутого на данную систему векторов $S = langle a_, a_, a_rangle.$
$$a_ = (1, 1, -1, -2), a_ = (5, 8, -2, -3), a_ = (3, 9, 3, 8).$$

Первым делом, найдем $b_$, $b_ = a_.$

Дальше найдем $b_.$ Из формулы пункта 2) мы видим, что: $$b_ = a_ + lambda_ cdot b_, lambda_ = dfrac<left(a_, b_right)><left(b_, b_right)>,$$ все необходимое для решения мы нашли, осталось только решить. Итак:$$lambda_ = -dfrac = -left(dfracright) = 3,$$ лямбду мы нашли, $b_$ у нас есть, теперь мы можем найти $b_:$ $$b_ = a_ + lambda_cdot b_ = (5, 8, -2, -3) + (-3, -3, 3, 6) = (2, 5, 1, 3).$$