Построить проекции центра окружности описанной вокруг треугольника авс (3 видео)

Решение основных задач способом замены плоскостей проекций

Решение четырех основных задач

Задача 1.Преобразовать комплексный чертеж так, чтобы прямая общего положения стала линией уровня.

Задача 2. Преобразовать комплексный чертеж так, чтобы прямая общего положения стала проецирующей.

Задача 3.Преобразовать чертеж так, чтобы плоскость общего положения в новой системе плоскостей проекций стала проецирующей.

Задача 4.Преобразовать чертеж так, чтобы плоскость общего положения стала плоскостью уровня.

Решение основных задач способом замены плоскостей проекций

1 Преобразовать прямую (АВ) общего положения в прямую уровня или, другими словами, определить натуральную длину отрезка [AB]. Построение новых проекций А₁, В₁ точек А, В выполняется по схеме рисунок 3.1.

Для решения этой задачи выбираем новую плоскость проекций параллельно данной прямой. На рисунке 3.2 новая фронтальная плоскость проекций П₄ выбрана параллельно АВ, т.е. новая ось х₁₄ выбрана параллельно горизонтальной проекции А₁В₁ прямой АВ. Проекция A₄B₄ на новой плоскости проекций П₄ определяется проекциями А₄, В₄ ее точек А,В, построенными по алгоритму, приведенному на рисунке 3.1.

Очевидно, эта задача также легко решается заменой горизонтальной плоскости проекций П₁ на новую плоскость проекций П₄. Для этого новую ось x₂₄=П₂ÇП₄ нужно выбрать параллельно фронтальной проекции А₂В₂ данной прямой.

2 Преобразовать прямую (АВ) общего положения в проецирующую прямую. Очевидно, эта задача при наложенных выше ограничениях на выбор новых плоскостей проекций не решается заменой одной плоскости проекций. Действительно, новую плоскость проекций нельзя выбрать одновременно перпендикулярной прямой АВ и одной из плоскостей проекций исходной системы.

а) б)
Рисунок 3.1	Рисунок 3.2

Рассмотрим решение этой задачи способом двух преобразований (рисунок 3.2). Преобразованием ƒ (П₂ П₄) прямую АВ проецируем на новую плоскость проекций в прямую уровня в системе П₁ П₄ (см. задачу 1). Вторым преобразованием ƒ(П₁ П₅), где новая плоскость проекций П₅ выбирается перпендикулярно АВ (А₄В₄^х₄₅), в системе П₄П₅ получаем проецирующую прямую А₅В_5.

3 Построить центр О окружности, описанной около треугольника АВC. Для решения этой задачи необходимо преобразовать плоскость общего положения в проецирующую. По условию задачи новая плоскость проекции должна быть перпендикулярной данной плоскости Ф(A₁B₁C₁, A₂B₂C₂). Это условие будет выполнено, если она будет перпендикулярна горизонтали h плоскости Ф при замене П₂ на П₄ или фронтали плоскости Ф при замене П₁ на П₅

На рисунке показано решение этой задачи заменой горизонтальной плоскости проекций П₁ на новую плоскость проекций П_4., где Ф П_4. Построение новых проекций А₄, В₄, С₄ точек А, В, С плоскости Ф ясно из рисунка.

4 Преобразовать плоскость общего положения Ф (А, В, С) в плоскость уровня, т. е. определить натуральные размеры треугольника ABC (рисунок 3.3).

Нетрудно показать, что решение этой задачи требует последовательного выполнения двух замен плоскостей проекций (способом двух преобразований), так как невозможно выбрать новую плоскость проекций, которая была бы одновременно параллельной плоскости Ф и перпендикулярной одной из плоскостей проекций исходной системы П₁ П₂.

Поэтому первой заменой ƒ(П₂ П₄) плоскость Ф преобразуем в проецирующую в системе П₁ П₄ (см. задачу 3),а второй заменой ƒ(П₁ П₅), где П₅ ||Ф, приводим ее в положение плоскости уровня в системе П₄ П₅.

Находим центр описанной окружности О₅ и возвращаем по обратной схеме на первоначальный комплексный чертеж.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Задача 68 Построить проекции центра окружности, описанной вокруг треугольника

Тип работы: Задача

Предмет: Начертательная геометрия

Статус: Выполнен

Год работы: 2020

Страниц: 1

Оригинальность: 100% (antiplagiat.ru)

Формат: программа КОМПАС

Цена: 200 руб.

Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

С помощью этой страницы вы сможете научиться решать задачи по начертательной геометрии:

Другие похожие задачи:

Описание работы:

Задача 68 Построить проекции центра окружности, описанной вокруг треугольника АВС, применив вращение вокруг фронтали, проходящей через вершину С.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Рабочая тетрадь

ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ

по начертательной геометрии

( для студентов, обучающихся по специальностям 110800 – «Агроинженерия», 190600.62 – «Эксплуатация транспортных и технологических машин и комплексов»

Студента 1-го курса. группы.

Курс ведут преподаватели:

Рабочую тетрадь составили:

Рекомендовано методическим советом Ставропольского

государственного аграрного университета к изданию.

Ответственный за выпуск, заведующий кафедрой «Механика и компьютерная графика» к. т.н., доцент

ТАБЛИЦА ДЛЯ СОПОСТАВЛЕНИЯ ЧАСТО ВСТРЕЧАЮЩИХСЯ ОБОЗНАЧЕНИЙ

Плоскости проекций: фронтальная

Оси проекций основные

Точки в пространстве

Линия в пространстве

Проекции отрезка прямой:

Плоскости и поверхности в пространстве

на дополнительной пл-сти

Рабочая тетрадь включает в себя обязательный минимум задач, предусмотренный действующей программой.

Программный материал курса занятий соответствует темам рабочей программы.

Каждая занятие содержит:

1. контрольные вопросы для проверки степени усвоения теоретического материала;

2. задачи для самостоятельных упражнений;

3. консультацию в виде методических указаний к решению задач или «графических ключей» построений (наглядного изображения решения наиболее трудных задач на пространственных чертежах для студентов, затрудняющихся самостоятельно их решить).

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

1. Перед каждым практическим занятием изучите теоретический материал темы по конспекту лекций и учебнику и -Огиевского «Курс начертательной геометрии».

2. На контрольные вопросы ответьте устно или лучше письменно (в отдельной тетради).

3. При подготовке к практическим занятиям рассмотрите решения типовых примеров, используя для этого «Сборник задач по начертательной геометрии» .

4. На практических занятиях решите обязательные задачи, которые обеспечивают закрепление теоретических основ курса и способствуют развитию навыков в проекционных построениях, если остаётся время, то переходите к решению оставшихся задач.

В случае затруднения в решении задачи ознакомьтесь с содержанием пункта «консультация».

Если и после этого Вы не можете самостоятельно решить задачу, обратитесь за помощью к преподавателю.

5. Проработав указанным образом материал занятия, переходите к работе над следующим.

Все построения следует выполнять простым черным карандашом марки «ТМ» или «М» при помощи линейки, треугольника, циркуля. Окончательный результат обведите красным карандашом.

Тема. Геометрические построения.

1. Как разделить отрезок прямой на две равные части?

2. Как построить правильный вписанный многоугольник?

3. Как разделить окружность на шесть равных частей?

4. Поясните суть способа триангуляции.

5. Где расположен центр окружности, описанной вокруг треугольника?

6. Как разделить угол на две равные части?

7. Как разделить угол на три равные части?

Задача 1.1. а)разделить отрезок АВ на две равные части с помощью циркуля и линейки;

б) Восстановить перпендикуляр к отрезку АВ, построив

одну вспомогательную окружность (дугу).

Построить проекции центра окружности описанной вокруг треугольника авс

Задача 1.2. Построить с помощью циркуля и линейки прямоугольник с заданной стороной АВ и стороной ВС =30 мм.

Задача 1.3. Разделить прямой угол на равные части.

Задача 1.4. Построить треугольник АВС с заданным новым положением стороны АВ.

Задача 1.5. Построить пятиугольник ABCDE с заданным новым положением стороны AB.

Задача 1.6. Найти центры кривизны дуг.

Задача 1.7. Описать окружность вокруг треугольника ABC.

Задача 1.8. Разделить окружность с помощью циркуля и линейки.

Задача 1.9. Построить касательную к окружности в точке А.

Задача 1.10. Построить правильный пятиугольник ABCDE по стороне AB.

1.Где расположена точка сопряжения двух дуг окружностей?

2.Что называется внешним сопряжением?

3.Что называется внутренним сопряжением?

4. Где расположен центр окружности, касательной к прямой?

5. Где расположен центр окружности, касательной к прямой в данной точке?

6. Где расположен центр окружности, касательной к двум пересекающимся прямым?

7. Где расположен центр окружности радиуса R, касательной к окружности радиуса r?

8. Где расположен центр окружности, касательной к данной окружности в данной точке?

9. Где расположен центр окружности, касательной к двум окружностям одинакового радиуса?

10. Какая линия называется коробовой кривой?

Задача 1.11. Выполнить сопряжения двух параллельных прямых.

Задача 1.12. Выполнить сопряжения прямой и дугой двух дуг радиусов R1 и R2 с центрами в точках О1 и О2 .

Задача 1.13. Выполнить сопряжения дуги и прямой дугами окружностей радиусов R1 = 30 мм, и R2= 30 мм.

Задача 1.14. Выполнить внешнее и внутреннее сопряжения дуги и прямой с заданной точкой сопряжения Т.

Задача 1.15. Выполнить сопряжения двух прямых с заданной точкой сопряжения Т.

Задача 1.16. Выполнить сопряжения двух окружностей с заданной точкой сопряжения Т.

Задача 1.17. Построить касательные к окружностям через

Тема. Плоские кривые. Многогранники. Поверхности.

Задача 1.18. Построить коробовую кривую по ширине AB = 100мм и высоте AB = 40 мм.

Задача 1.19. Построить овал по осям AB и CD.

Задача 1.20. Построить овоидальную кривую размера AB.

Задача 1.23. Построить эллипс

б) по большой AB и малой CD осям.

Задача 1.24. Построить параболу по заданному параметру р.

Задача 1.26. Построить из точки О по заданному шагу спираль Архимеда.

Задача 1.27. Построить циклоиду.

Задача 1.28. Построить гипоциклоиду.

Задача 1.29. Построить эпициклоиду.

Задача 1.30. Построить синусоиду.

Задача 1.31. Построить эвольвенту круга.

Задача 1.31. Построить правильную пятигранную призму высотой 30мм, стороной основания, вписанной в окружность.

Задача 1.32. Построить правильную трёхгранную пирамиду высотой 40мм и стороной основания, вписанной в окружность.

Задача 1.33. Построить три вида конуса и три вида цилиндра высотой 40 мм и радиусом основания 20мм.

Тема. Задание точки на комплексном чертеже Монжа.

1. Как расположены на эпюре проекции одной и той же пространственной точки относительно:

2. Каков порядок построения по двум заданным проекциям точки третьей?

Задача 2.1. Постройте проекции точки А, находящейся:

1) в первой четверти пространства

2) в третьей четверти пространства

Задача 2.2. Постройте проекции точки А при условии, что ZA=0

При построении проекций точек на пространственном чертеже перпендикуляры, опускаемые из данной точки на плоскости проекции, проводите параллельно осям Х0, У0, Z0.

1. Чем измеряется на эпюре расстояние от точки в пространстве до плоскостей проекции?

2. Какие координаты определяют горизонтальную, фронтальную и профильную проекции точки?

Задача 2.3. Постройте эпюр точки А по заданным координатам:

(координаты указаны в мм)

Так как отрицательные координаты отмеряются в направлениях, противоположных положительным, при построении горизонтальной

проекции точки на эпюре отрезок, определяющий отрицательную координату «Y« отложите вверх от оси Х0, а при нахождении профильной проекции точки – влево от оси Z0.

Тема. Задание прямой на комплексном чертеже Монжа.

1. Что характерно на эпюре для:

а) прямых общего положения;

б) прямых, параллельных одной из плоскостей проекций;

в) прямых, перпендикулярных одной из плоскостей проекций.

Задача 3.1. Постройте проекции прямой АВ на пространственном чертеже и выполните ее эпюр, если прямая:

1) параллельна горизонтальной плоскости проекций (Н)

2) параллельна фронтальной плоскости проекций (V):

3) перпендикулярна горизонтальной плоскости проекции:

4) перпендикулярна фронтальной плоскости проекций:

5) параллельна оси проекций (Х0):

Задача 3.2. Постройте эпюр отрезка АВ если он:

1) общего положения, находится во второй четверти пространства и упирается концом А в фронтальную плоскость проекций.

2) находится в первой четверти пространства, расположен параллельно фронтальной плоскости проекций и упирается концом А в горизонтальную плоскость проекций.

3) лежит произвольно на передней поле горизонтальной плоскости проекций.

4) находится в третьей четверти пространства, расположен перпендикулярно горизонтальной плоскости проекций и его конец А одинаково удален от плоскостей проекций Н и V.

Тема: Взаимное положение точки прямой.

Взаимное положение двух прямых

1. Как определить взаимную принадлежность точки и прямой по эпюру?

2. Как построить по одной заданной проекции точки, принадлежащей профильной прямой, недостающие ее проекции?

3. Что характерно для эпюра прямых?

4. Как определить по эпюру, что прямые скрещивающиеся?

5. Как по эпюру определить взаимное положение двух профильных прямых?

Задача 4.1 (1,2) Найти на прямой АВ точку, если дано ее расстояние от какой-либо плоскости проекций.

К задаче 4.1 (1,2) Используя заданную координату, постройте одну проекцию точки, остальные проекции точки найдите на одноимённых проекциях прямой, как недостающие при одной заданной.

Задача Определить взаимное положение прямых по эпюру.

1. Что называется следом прямой?

2. Как располагаются на эпюре проекции:

а) фронтального следа прямой;

б) горизонтального следа прямой;

3. Какие прямые имеют в системе плоскостей проекций Н, V, W:

а) только один след?

Задача 5.1. Постройте проекции прямой по заданным ее следам.

Задача 5.2. Найдите проекции следов прямой, проходящей через точки А и В.

Задача 5.3 (1,2) Найдите проекции следов прямой АВ.

К задаче 5.1. 1) Найдите по две проекции каждого из заданных следов прямой, исходя из того, что след прямой есть точка, лежащая в плоскости проекций. Соедините одноименные проекции следов прямой.

2) Графический ключ решения задачи.

К задаче 5.2. Соедините одноименные проекции точек А и В и найдите проекции следов заданной прямой.

К задаче 5.3. 1) До решения задачи представьте себе в пространстве положения заданной прямой и определите количество следов в системе плоскостей проекций Н, V.

2) Графический ключ решения задачи.

Тема: Метрические задачи. Позиционные задачи. Метод прямоугольного треугольника. Свойства проекций прямого угла.

1. При каком расположении отрезка прямой относительно плоскостей Н, V, W его проекция изображает действительную величину?

2. Как определить углы наклона прямой к плоскостям проекции?

3. Как определить по эпюру действительную величину отрезка прямой общего положения и углы наклона его к плоскостям проекций?

4. В каком случае любой угол проецируется в действительную величину?

5. В каком случае прямой угол проецируется в действительную величину?

Задача 6.1. Определить действительную длину отрезка прямой АВ и углы ее наклона к плоскостям Н и V?

Задача 6.2. Определить расстояние от точки А до прямой ВС.

Задача 6.3. Определить расстояние между прямыми АВ и СД.

К задаче 6.2. Для решения задачи нужно точку А и отрезок прямой ВС заключить в «жесткий» треугольник, построить его по действительным размерам трех сторон и опустить перпендикуляр из точки А на прямую ВС.

К задаче 6.3. 1) Для решения задачи задайте точку на одной из прямых и опустите из нее перпендикуляр на другую прямую.

Тема. Задание плоскости на комплексном чертеже Монжа.

Точка на плоскости

1. Какими способами задаются плоскости на эпюре?

2. Как провести на эпюре заданной плоскости прямую, принадлежащую ей?

3. Что такое горизонталь и фронталь плоскости и в какой последовательности строят их проекции на эпюре?

Задача 7.1. Задайте на плоскости произвольную точку:

а) с помощью произвольной прямой;

б) с помощью горизонтали;

в) с помощью фронтали.

Задача 7.2. Найдите недостающую проекцию точки К, лежащей на заданной плоскости:

а) с помощью произвольной прямой;

б) с помощью горизонтали;

в) с помощью фронтали.

Задача 7.3. По заданным проекциям точки и плоскости определите, лежит ли точка К в плоскости (используя любые прямые).

К задаче 7.1 (а). Перейдите к заданию плоскости треугольником, двумя параллельными или пересекающимися прямыми.

К задаче 7.1 (б). Постройте горизонталь на эпюре, начиная с проведения ее фронтальной проекции.

К задаче 7.1 (в). Постройте фронталь на эпюре, начиная с проведения ее горизонтальной проекции.

Тема: Задание плоскости следами

1. Что называется следом плоскости?

2. В чем условность задания плоскости следами на эпюре?

3. Где на эпюре находятся следы прямой, принадлежащей плоскости?

Задача 8.1. Определите недостающее проекции точек, лежащих в плоскости Р.

Задача 8.2. Дана фронтальная проекция треугольника АВС, лежащего в плоскости Р. Определите его горизонтальную проекцию:

1) пользуясь фронталями плоскости Р

2) пользуясь горизонталями плоскости Р

3) пользуясь прямыми общего положения.

Задача 8.3. Дана одна из проекций треугольника АВС, лежащего в профильно-проецирующей плоскости. Определите другую ее проекцию:

1) пользуясь профильной плоскостью проекций

2) не пользуясь профильной плоскостью проекций

К задаче 8.1. Графические ключи решения задачи:

а) пользуясь фронталью плоскости Р:

б) пользуясь горизонталью плоскости Р:

в) пользуясь прямой общего положения

К задаче 8.2 (1,2). Горизонтальные проекции вершин треугольника найдите как недостающие проекции точек, лежащих в плоскости.

К задаче Профильная проекция искомого треугольника должна лежать на профильном следе плоскости Р. Горизонтальная проекция треугольника АВС определяется, как недостающая, по двум заданным.

К задаче 1) Горизонтальные проекции точек А, В, С найдите с помощью произвольных прямых, лежащих в плоскости Р и проходящих через точку К и каждую из вершин треугольника.

2) Графический ключ решения задачи (показано нахождение горизонтальной проекции точки А)

Тема 3. Позиционные задачи. Метрические задачи.

1. Что нужно найти для построения линии пересечения двух плоскостей в общем случае?

2. В чем состоит упрощение в нахождении линии пересечения двух плоскостей, заданных следами?

3. Как найти следы линии пересечения двух плоскостей, заданных следами?

Задача 9.1 Найдите линию пересечения плоскостей Р и Q;

а) не вводя вспомогательной плоскости

б) вводя вспомогательную плоскость

Задача 9.2. Найдите горизонтальные следы двух плоскостей Р и Q, если известны их фронтальные следы и точка К, принадлежащая линии их пересечения.

К задаче 1) Найдите проекции следов линии пересечения двух плоскостей;

2) Графический ключ решения

К задаче 9.1(2). Графический ключ решения

К задаче Графический ключ решения

К задаче 1) Используйте свойство проецирующих плоскостей;

2) графический ключ решения

К задаче Графический ключ решения

К задаче 1) Введите плоскость-посредник через точку К и решите задачу по общей схеме;

2) графический ключ решения

К задаче 9.2. 1) Проведите через точку К прямую, вначале в плоскости Р, потом в плоскости Q.

2) Найдите следы заданных прямых.

3) Через горизонтальные следы этих прямых проведите искомые следы плоскостей Р и Q.

Задача 9.3. Найдите линию пересечения плоскости треугольника АВС с плоскостью Р.

Тема: Позиционные и метрические задачи.

Взаимное положение прямой и плоскости

1. Какова последовательность построения точки встречи прямой с плоскостью в общем случае?

2. Как находится точка встречи прямой с плоскостью, если один из заданных элементов задачи проецирующий?

3. Сформулируйте условие параллельности прямой и плоскости.

Задача 10.1. Найдите точку пересечения прямой АВ с плоскостью Р.

Задача 10.2. Найдите точку пересечения прямой АВ с плоскостью, заданной треугольником АВС.

Задача 10.3. Проведите через точку А прямую, параллельную плоскости Р.

Задача 10.4. Проведите через точку А две прямые, параллельные плоскости, заданной прямой ВС и точкой Д.

К задаче 10.1.(3) 1) Используйте общий прием решения задачи. Заключите прямую в горизонтально-проецирующую плоскость.

2) Графический ключ решения

М — искомая точка встречи прямой АВ с плоскостью Р.

К задаче 10.1(4). Используйте свойство проецирующей плоскости.

К задачам 10.3, 10.4. В заданной плоскости проведите любые прямые (общего положения или линии уровня). Решение многозначно.

Тема 3. Позиционные задачи. Метрические задачи. Взаимное положение двух плоскостей

1. Сформулируйте условие параллельности двух плоскостей общего положения:

а) заданных не следами;

б) заданных следами.

2. Как формулируется условие параллельности двух профильно-проецирующих плоскостей?

Задача 11.2. Найдите недостающий след плоскости Q, исходя из условия, что Q // Р:

Задача 11.3. Постройте следы плоскости, проходящей через точку К и параллельной плоскости Р.

К задаче 1 Чтобы выяснить, параллельны ли плоскости Р и Q, следует воспользоваться двумя пересекающимися прямыми, проведенными в каждой плоскости. Для упрощения решения в качестве одной из указанных прямых используйте один из следов каждой заданной плоскости.

К задаче 1 Искомый горизонтальный след плоскости Q должен проходить через горизонтальный след прямой, проведенной в этой плоскости и параллельной прямой, лежащей в плоскости Р.

К задаче 11.3. Для решения предварительно проведите через точку К прямую, параллельную плоскости Р, и заключите ее в искомую плоскость.

1. Сформулируйте условие перпендикулярности прямой и плоскости в пространстве.

2. Как построить на эпюре прямую, перпендикулярную плоскости, в случае: а) задания плоскости не следами?

б) задания плоскости следами?

3. Вспомните условие перпендикулярности двух плоскостей.

4. Почему две плоскости общего положения не перпендикулярны, если их одноименные следы взаимно-перпендикулярны?

Задача 11.4. Определите расстояние от точки К до плоскости.

Задача 11.6. Опустите из точки С перпендикуляр на прямую АВ.

Задача 11.7. Проведите через прямую АВ плоскость, перпендикулярную к плоскости Р.

К задаче 11.4. Постройте направление проекций перпендикуляра к плоскости, найдите его основание (точку пересечения с плоскостью) и определите истинную величину полученного отрезка перпендикуляра.

К задаче 11.5. Задайте в одной из плоскостей точку (проще всего взять ее на следе плоскости), постройте из проекции этой точки направление проекций перпендикуляра к плоскости. Дальнейший ход решения рассматривался в задачах ранее.

К задаче 11.6. Искомый перпендикуляр должен лежать в плоскости, проведенной через заданную точку С, перпендикулярно к прямой АВ.

1. Графический ключ решения

Тема. Способы преобразования эпюра.

1. Вспомните сущность метода перемены плоскостей проекций.

2. Можно ли одновременно заменить две плоскости проекций?

3. Какие координаты не изменяются при замене:

4. Как следует произвести замену плоскостей проекций, чтобы плоскость общего положения стала плоскостью уровня?

5. В чем состоит сущность метода плоскопараллельного перемещения?

6. Какие координаты, форма и размеры какой проекции фигуры остаются неизменными при ее перемещении в плоскости:

а) параллельной V ? б) параллельной Н ?

Задача 12.1. Используя метод замены плоскостей проекций, постройте проекции треугольника АВС в новой системе так, чтобы его горизонтальная проекция представляла натуральную величину треугольника.

Задача 12.2. Переместите треугольник так, чтобы его горизонтальная проекция представляла натуральную величину.

К задаче 12.1. Задача решается двумя последовательными заменами плоскостей проекций. Вначале заменяем одну из плоскостей проекций, располагая ее перпендикулярно к треугольнику, после чего ставим другую плоскость проекций параллельно треугольнику.

К задаче 12.2. Вначале, перемещая треугольник параллельно одной из плоскостей проекций, преобразуйте его в плоскость проецирующую, последующим перемещением треугольника параллельно другой плоскости проекций, преобразуйте его в плоскость уровня.

Тема. Многогранники. Кривые линии. Поверхности.

1. Какие вы знаете способы построения проекций фигуры сечения многогранника плоскостью общего положения?

2. Какими способами определяют истинную величину фигуры сечения?

3. Какой способ применяется для построения проекций фигуры сечения поверхности вращения плоскостью общего положения?

4. Как построить развертку боковых поверхностей прямых круговых цилиндра и конуса?

5. Какой способ применяется для построения проекций фигуры сечения поверхности вращения плоскостью общего положения?

6. Как построить развертку боковых поверхностей прямых круговых цилиндра и конуса?

К задаче 13.1. Задача может быть решена одним из способов:

1-й способ. Воспользуйтесь плоскостями-посредниками, проведя их через ребра призмы (или через грани призмы). Истинный вид сечения определите с помощью одного изметодов преобразования эпюра.

2-й способ. Для построения проекций фигуры сечения используйте то обстоятельство, что боковые грани призмы является проецирующей по отношению к плоскости Н.

3-й способ. Преобразуйте секущую плоскость в проецирующую одним из способов преобразования эпюра, тогда одна из проекций фигуры сечения превратится в прямую.

Задача 13.1. Постройте полную развертку одной из частей призмы, пересеченной плоскостью Р.

Тема. Многогранники. Кривые линии. Поверхности.

Задача 14.1. Постройте полную развертку одной из частей кругового конуса, пересеченного плоскостью Р.

К задаче 14.1. Искомая фигура сечения представляет часть эллипса, для построения которого определите вначале характерные (опорные) точки, используя метод плоскостей-посредников или применив один из методов преобразования эпюра. Для получения развертки усеченной части конуса постройте развертку полного конуса, вписав в него предварительно двенадцатигранную пирамиду. Затем на развертке на каждой образующей (ребре пирамиды) отложите истинную величину отрезков, образующих отсеченной части конуса.

Тема. Обобщённые позиционные задачи.

Пересечение прямой с поверхностью

1. В чем заключается общий прием решения задач на пересечение прямой с поверхностью?

2. Какими плоскостями-посредниками удобнее пользоваться для нахождения точек встречи прямой с поверхностью многогранника?

3. Какие плоскости-посредники применяют для нахождения точек встречи прямой общего положения с поверхностями вращения?

Задача 15.1. Найдите точки пересечения прямой с поверхностью пирамиды.

1. Какой способ целесообразно применять для определении точек пересечения прямой с поверхностью шара?

Задача 15.2. Найдите точки пересечения прямой с поверхностью тела вращения.

К задаче 15.1. Для определения точек пересечения прямой АВ с пирамидой удобно воспользоваться проецирующей плоскостью, заключая в нее прямую.

К задаче 1 1) Заключите прямую в плоскость общего положения, параллельную оси цилиндра.

2) Графический ключ решения

К задаче 1 1) Заключите прямую в плоскость общего положения, которая пересекла бы поверхность конуса по образующим.

2) Графический ключ решения

К задаче 1 1) Примените один из известных Вам способов преобразования эпюра для того, чтобы прямую преобразовать в линию уровня. После этого используйте общий прием решения.

2) Графический ключ решения

Тема: Обобщенные позиционные задачи. Метрические задачи. Построение линии пересечения поверхностей методом вспомогательных секущих плоскостей.

1. Что нужно найти, чтобы построить проекцию линии пересечения двух поверхностей вращения?

2. Какова последовательность построения проекций точек искомой линии пересечения двух поверхностей?

3. Что нужно учитывать при выборе плоскостей-посредников?

Задача 16.1. Используя плоскости-посредники, постройте линию пересечения двух поверхностей.

К задаче 1Для построения горизонтальной проекции линии пересечения поверхностей воспользуйтесь плоскостями уровня

или используя параллели конуса. Предварительно найдите опорные точки искомой линии.

К задаче 1 Для решения в качестве секущих плоскостей-посредников используйте плоскости уровня.

Тема: Обобщенные позиционные задачи. Метрические задачи. Построение линии пересечения поверхностей методом вспомогательных секущих поверхностей

1. В чем сущность способа концентрических сфер?

2. Какая теорема положена в основу способа сфер?

3. Вспомните условие применения метода концентрических сфер для построения проекций линии взаимного пересечения двух поверхностей?

Задача 17.1. Постройте линию пересечения двух поверхностей способом концентрических сфер.

К задаче 17.1. Найдите характерные (опорные) точки искомой кривой. В качестве центра концентрических сфер примите точку пересечения осей вращения двух поверхностей вращения.

Тема. Аксонометрические проекции.

1. Какие виды аксонометрических проекций по направлению лучей относительно картинной плоскости известны?

2. Чем отличаются изометрическая, диметрическая и триметрическая проекции?

3. Какая кривая будет аксонометрической проекцией окружности?

Задача 18.1. Построить прямоугольные изометрические проекции с вырезом четверти:

Задача 18.2 . Построить прямоугольные диметрические проекции с вырезом четверти:

а) конуса.

1. Положение аксонометрических осей и масштабы измерений по осям для аксонометрических проекций:

2. Направление штриховки в аксонометрических разрезах и масштабы измерений по осям для аксонометрических проекций:

💥 Видео

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Построить описанную окружность (Задача 1)Скачать

Построение натуральной величины треугольника методом вращенияСкачать

Построение проекции пирамиды. Метод прямого треугольника.Скачать

ПОСТРОИТЬ ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА ПО ЗАДАННЫМ УСЛОВИЯМ. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.Скачать

СПОСОБ ПЕРЕМЕНЫ ПЛОСКОСТЕЙСкачать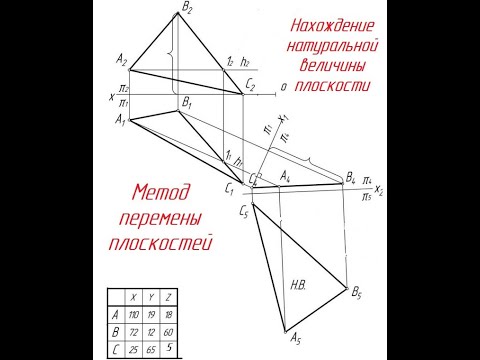

Начертательная геометрияСкачать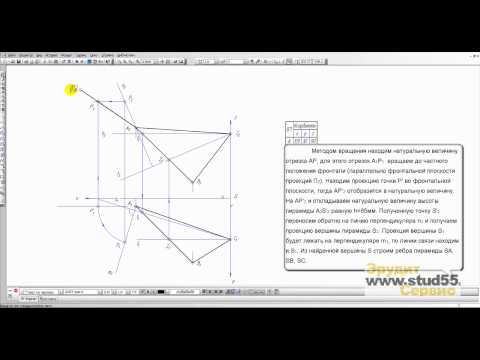

Способ вращения. Определение истинной величины отрезка.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Построение призмы высотой 30ммСкачать

Построение недостающих проекции сквозного отверстия в сфереСкачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Построение треугольника в трёх проекцияхСкачать

Натуральная величина треугольника (метод вращения)Скачать

Вращение вокруг проецирующей прямой и прямой уровняСкачать