- Геометрия как искусство: 4 и 8 (часть третья)
- Фигуры
- Квадрат (лежащий на одной из сторон)
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6
- Шаг 7
- Динамичный квадрат (вписанный в окружность)
- Шаг 1
- Шаг 2
- Шаг 3
- Статический квадрат (на основе вписанной окружности)
- Шаги 1-2
- Шаг 3
- Шаг 4
- Шаг 5
- Статическая и динамическая четырехконечные звезды
- Шаг 6
- Шаг 7
- Статические октагон и октаграмма (вписанные в квадрат)
- Шаг 1
- Шаг 2
- Шаги 3-5
- Шаг 6
- Динамичный октагон (вписанный в круг)
- Шаги 1-4
- Шаг 5
- Шаг 6
- Узоры
- Сетка пяти окружностей
- Шаг 1
- Шаг 2
- Шаги 3 и 4
- Шаг 5
- Шаг 6
- Шаг 7
- Шаг 8
- Шаг 9
- Узор из динамичных октагонов
- Дыхание милостивого
- Шаг 1
- Шаг 2
- Шаг 3
- Узор из статичных октагонов
- Шаг 1
- Квадрат вписанный в окружность
- Определение
- Формулы
- Радиус вписанной окружности в квадрат
- Радиус описанной окружности около квадрата
- Сторона квадрата
- Площадь квадрата
- Периметр квадрата
- Диагональ квадрата
- Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.
- ИЗОБРАЖЕНИЕ ВПИСАННЫХ И ОПИСАННЫХ ОКОЛО ОК-РУЖНОСТИ МНОГОУГОЛЬНИКОВ
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Дистанционные курсы для педагогов
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Квадрат вписанный в окружность
- Определение
- Формулы
- Радиус вписанной окружности в квадрат
- Радиус описанной окружности около квадрата
- Сторона квадрата
- Площадь квадрата
- Периметр квадрата
- Диагональ квадрата
Видео:Как вписать квадрат в окружностьСкачать

Геометрия как искусство: 4 и 8 (часть третья)
Эта статья — продолжение цикла переводов, посвященных геометрии и тому, как она работает в искусстве. О том, чем рисовать и как читать схемы, можно прочитать в предыдущих частях (инструменты и базовые построения).
Прим.пер. — Если кому-то неинтересно возиться с карандашом и циркулем, в комментариях к оригиналу подсказывают, что с построениями можно попробовать поиграть в Adobe Illustrator. С точки зрения практической реализации я не советчик, но идея симпатичная. Дерзайте)
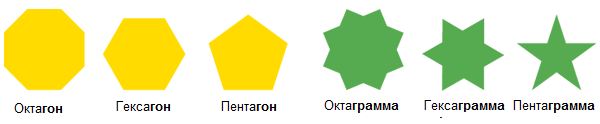
Сегодня разбираемся с геометрией чисел 4 и 8, то есть строим квадраты, октагоны, октаграммы и несколько узоров, на них основанных. Но для начала определимся с терминами:
- Слова, оканчивающиеся на –гон обозначают фигуру с количеством сторон n (выпуклый многоугольник). У октагона восемь сторон, у декагона – десять и так далее.
- Слова, оканчивающиеся на –грамма обозначают n-конечную звезду (звездчатый многоугольник). Октограмма – восьмиконечная звезда, гексаграмма – шестиконечная и так далее.
Если для каждого числа сторон существует единственный правильный выпуклый многоугольник, то звездчатых, наоборот, будет несколько, в зависимости от того, как соединяются точки. Чем больше лучей, тем больше вариантов. (прим. пер. – Вообще, кому интересно, на википедии написано чуть подробнее, и есть понятная картинка)
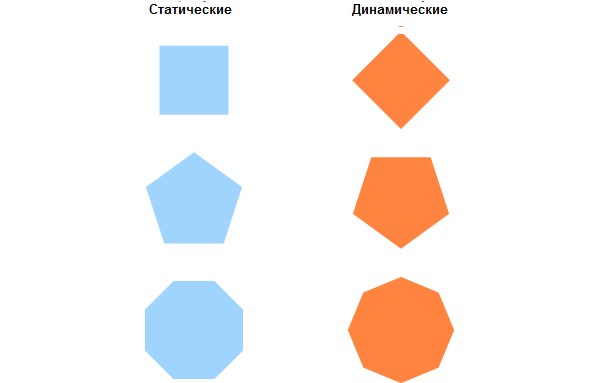
Еще два понятие, которые мы часто будем использовать для описания фигур – статическая и динамическая. Статическая лежит на своей стороне, динамическая – опирается на угол.
Эти определения довольно точно выражают чувства, которые вызывают эти фигуры. (Да, геометрия и чувства в одном предложении, вы не ослышались.)
При построении любой фигуры мы должны сперва решить, будет ли она статической или динамической, так как от этого будет зависеть выбор метода построения. И не только от этого: мы далеко не всегда начинаем с нуля, часто нужно вписаться в имеющиеся построения, начать с заданной точки, сегмента, окружности, соотношения. Каждая из этих ситуаций требует особого подхода.
Я не буду рассматривать все, потому что тысячи их, но покажу как минимум по паре для каждой фигуры, чтобы вы попробовали строить всякие штуки по-разному.
Видео:Как построить квадрат, два способаСкачать
Фигуры
Видео:Изображение в изометрической проекции окружностей, вписанных в кубСкачать

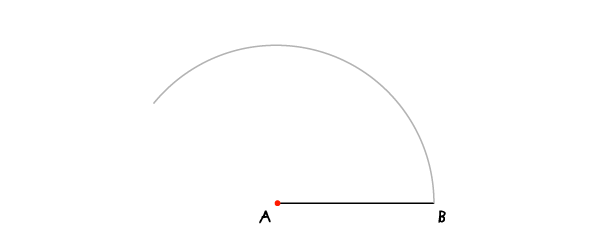
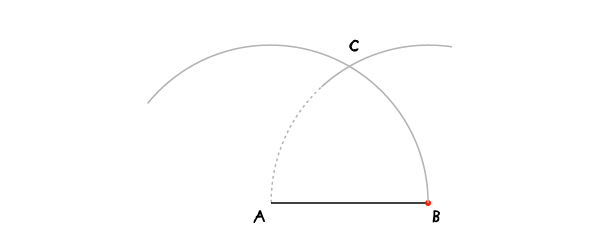
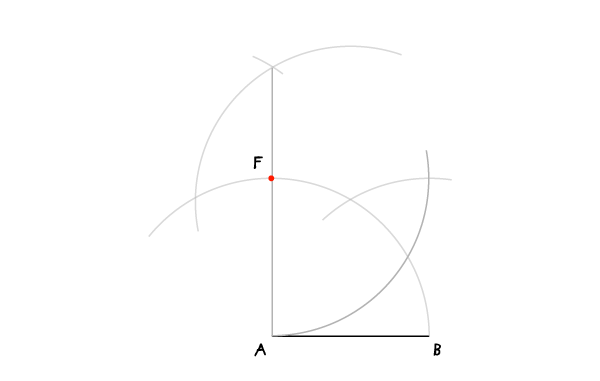
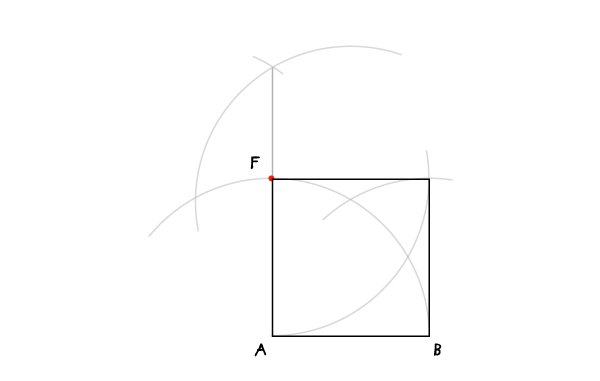
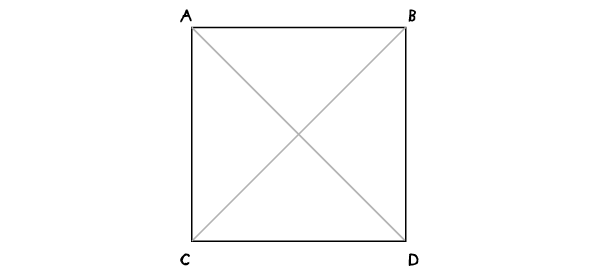
Квадрат (лежащий на одной из сторон)
В соответствии с заголовком этот метод используется, когда одна из сторон квадрата задана или когда вам надо с чего-то начать (в этом случае до Шага 1 проведите сторону, на которой будете строить свой квадрат).
Шаг 1
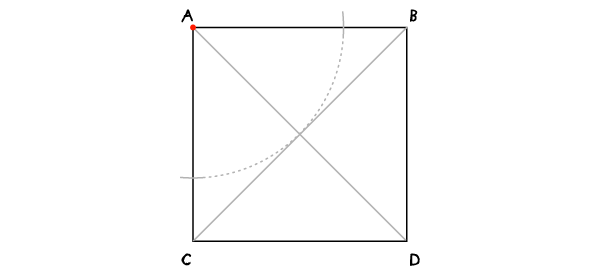
С раскрывом циркуля на АВ проведите дугу с центром в А. Во всех дальнейших построениях раскрыв циркуля останется неизменным.
Шаг 2
Переместите иглу в точку В и проведите дугу, пересекающую первую в точке С.
Шаг 3
Переместите иглу в точку С и проведите дугу, также пересекающую первую (с центром в А) в точке D.
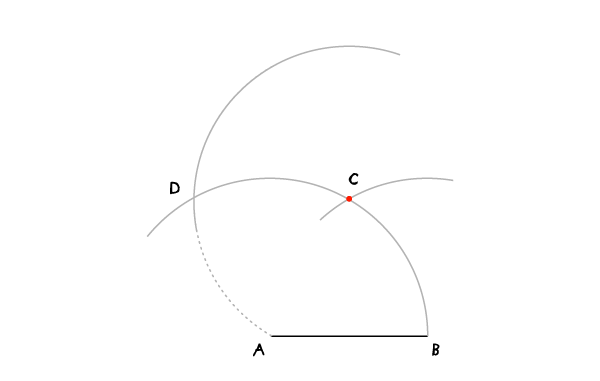
Шаг 4
Переместите иглу в D и проведите дугу, пересекающую проведенную в шаге 3 в точке E.
Шаг 5
Соедините Е и А, чтобы найти F. В это мы проделали для того, чтобы найти перпендикуляр к АВ через точку А.
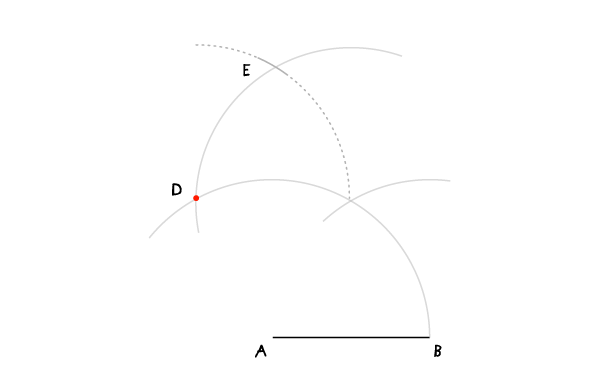
Шаг 6
Последняя дуга: поместите иглу в точку F и проведите дугу, чтобы найти точку G. Эту дуга будет пересекать дугу с центром в В.
Шаг 7
Соедините G, Fи B, чтобы закончить построение квадрата.
Хотя описанный метод и полезен, я заметила, что традиционно в искусстве отдают предпочтение другому, тому, где построение начинается от заданной окружности. Возможно, это дань символизму, напоминание о Единице (символ которой – окружность), начале всех начал, а возможно, он просто более ясный.
Однако, совсем отказываться от предыдущего метода не стоит. Если все, что у вас есть, это древнющий ржавый циркуль, раскрыв которого раз и навсегда установил еще ваш прадедушка, то следующий метод вам не подойдет.
Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

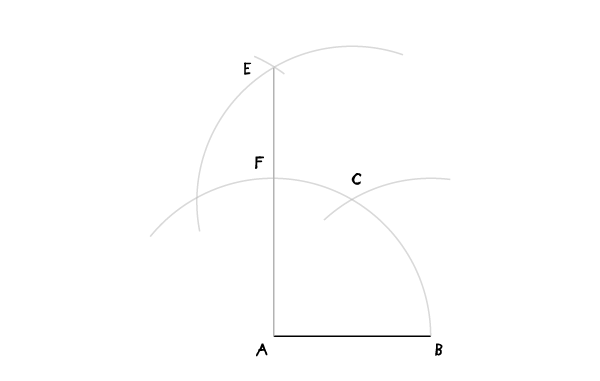
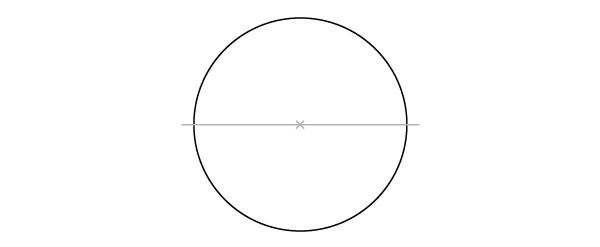
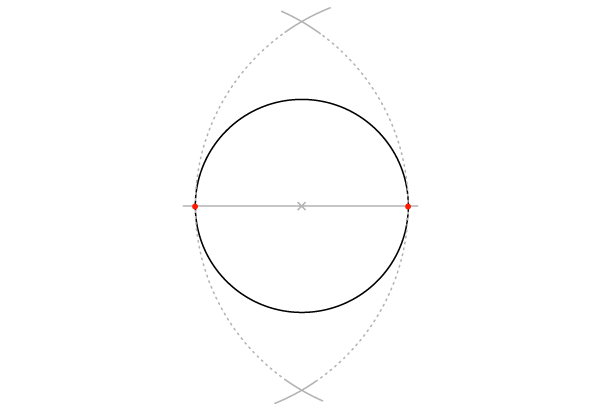
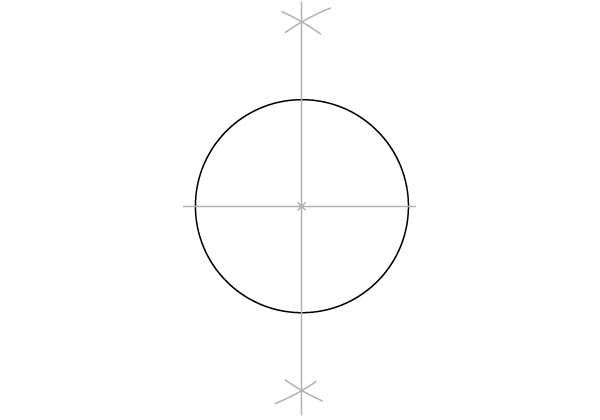
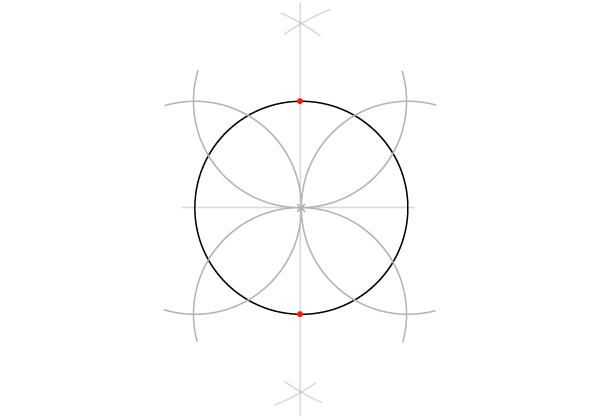
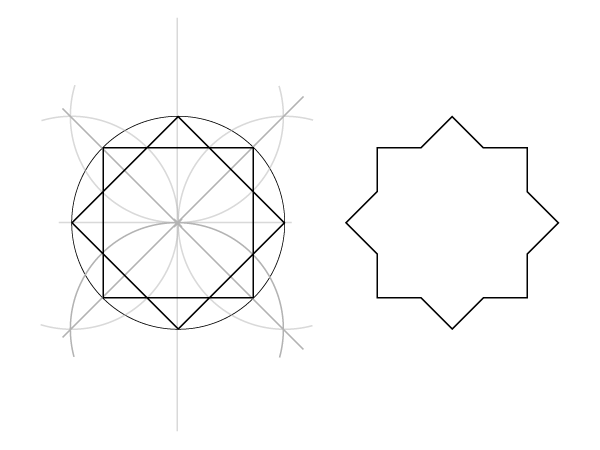
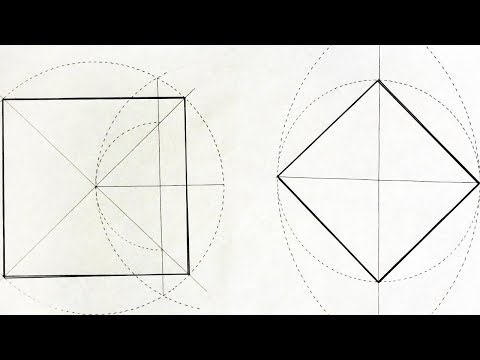
Динамичный квадрат (вписанный в окружность)
Наша отправная точка– окружность с одним проведенным диаметром. Начали вы с диаметра или с окружности – неважно.
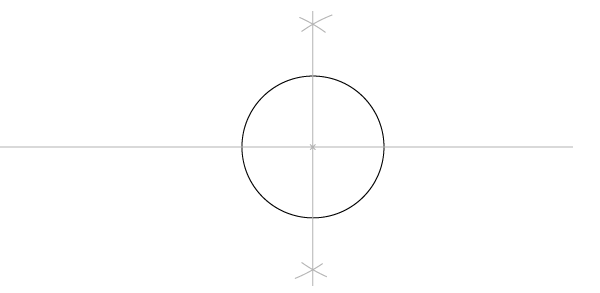
Шаг 1
Постройте перпендикуляр к диаметру, делящий его пополам, как во второй части(ссылка). Начните с рисования двух пересекающихся дуг…
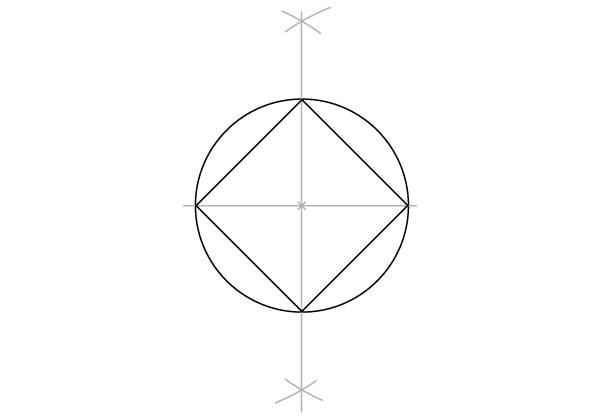
Шаг 2
… и соедините две точки пересечения. Перпендикуляр пересечет окружность в двух точках, и мы таким образом получим 4 определенные точки на окружности.
Шаг 3
Соедините 4 точки.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

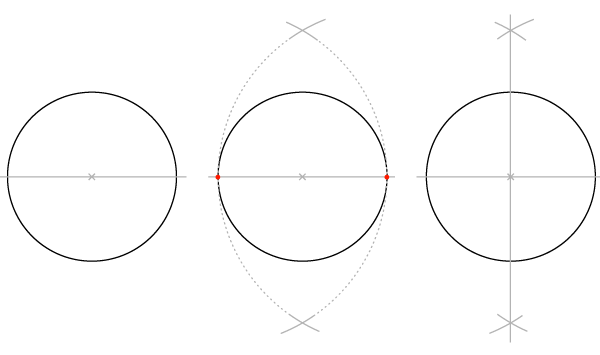
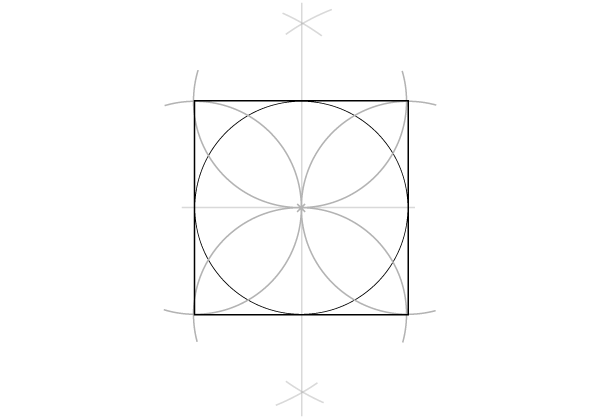
Статический квадрат (на основе вписанной окружности)
Шаги 1-2
Те же, что в прошлый раз: начинаем с круга с горизонтальным диаметром, ищем перпендикуляр так, чтобы окружность оказалась разделена на 4 части.
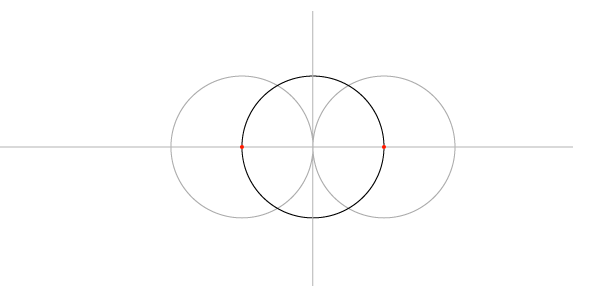
Шаг 3
Устанавливаем раскрыв циркуля равным радиусу и проводим две дуги с центрами в двух начальных точках. Точкой соприкосновения дуг окажется центр окружности.
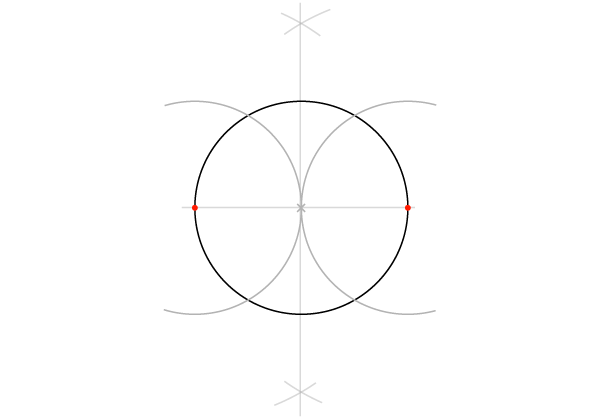
Шаг 4
Повторяем то же для двух точек, полученных после построения перпендикуляра. Эти 4 дуги определяют 4 точки, лежащие вне окржности.
Шаг 5
Соедините 4 точки.
Теперь только два шага отделяют нас от того, чтобы получить две четырехконечные звезды.
Видео:Как построить шестиугольник вписанный в окружностьСкачать

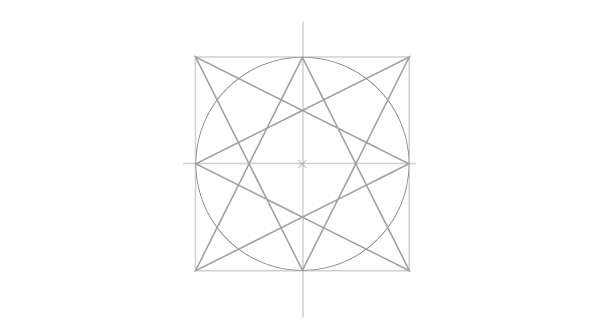
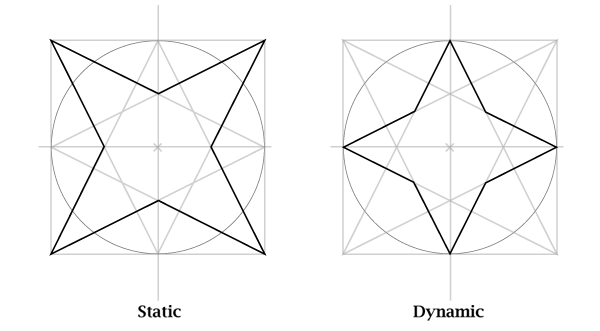
Статическая и динамическая четырехконечные звезды
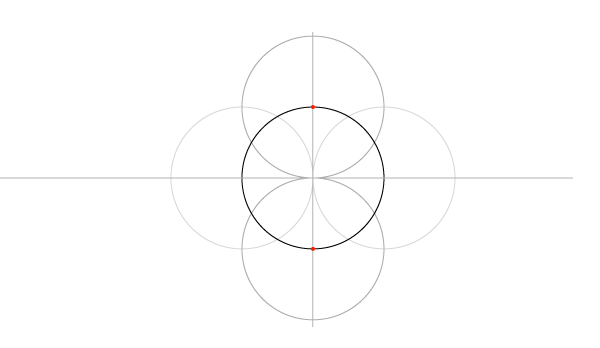
Шаг 6
Соедините 4 точки, лежащие на окружности с 4 углами статического квадрата, как показано на рисунке:
Шаг 7
Обведите нужную вам звезду.
Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

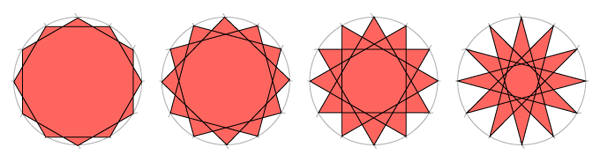
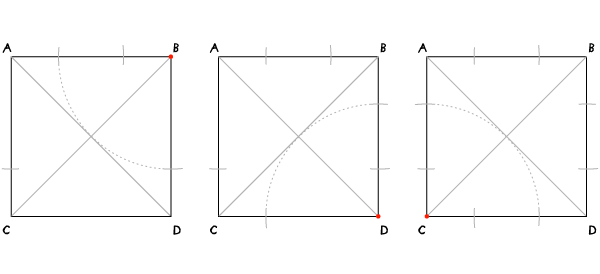
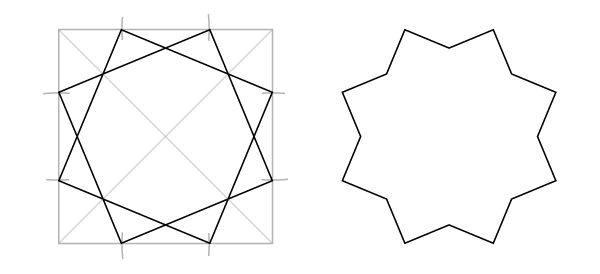
Статические октагон и октаграмма (вписанные в квадрат)
Шаг 1
Начните с квадрата, проведите диагонали.
Шаг 2
Установите иглу в А и с раскрывом циркуля от А до центра квадрата найдите две точки на сторонах квадрата.
Шаги 3-5
Повторите шаг 2 для точек В, С и D.
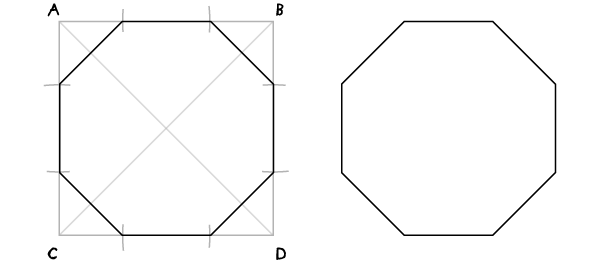
Шаг 6
Для октагона: соедините восемь найденных точек.
Для октаграммы соедините точки как показан на рисунке. Получится, что вы соединяете точки через одну. Обратите, что классическая октаграмма образована при взаимном повороте двух квадратов.
Еще одну октаграмму можно получить, если пропускать точки через две.
Обратите внимание, что меньшая октаграмма точно вписывается в большую.
Видео:Построить описанную окружность (Задача 1)Скачать

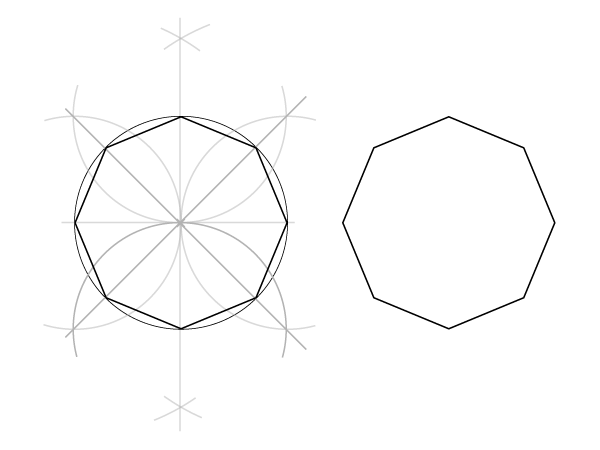
Динамичный октагон (вписанный в круг)
Шаги 1-4
Такие же, как при построении статического октагона. Остановитесь до момента, когда нужно соединять точки.
Шаг 5
Соедините внешние точки по диагонали. Диагонали пересекут окружность в новых 4 точках, то есть теперь она разбита на 8 частей.
Шаг 6
Для динамичного октагона соедините эти 8 точек.
Для динамичной октаграммы соедините точки через одну, как показано ниже, нарисовав два квадрата.
плитки из центрального Ирана, XIV век
Видео:Геометрия - Построение шестиугольникаСкачать

Узоры
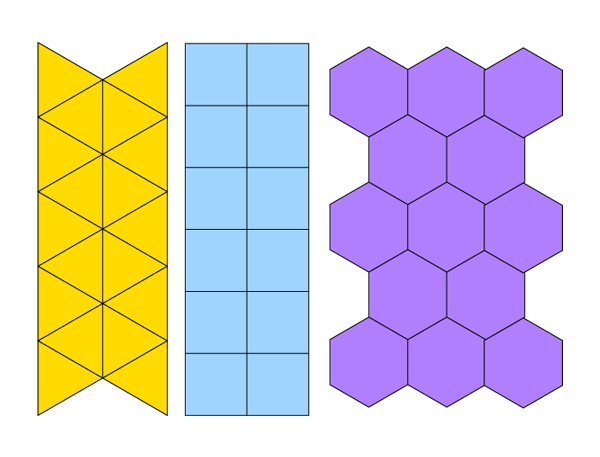
До настоящего момента мы строили только отдельные фигуры, теперь у нас достаточно знаний, чтобы начать складывать из этих фигур мозаичные узоры. Что еще нужно знать перед началом работы с мозаикой: только квадраты, а также равносторонние треугольники и шестиугольники складываются друг с другом, не оставляя между собой пустот.
Все прочие, включая октагоны, приведут к появлению промежутков различной формы. Это является недостатком, например, при выборе формы упаковки, поскольку при перевозке проявляется нерациональное использование пространства. В случае с искусством никакой это не недостаток: небольшие пространства работают в противовес крупным формам, позволяя создать контраст по цвету и размеру, или, наоборот, в слиянии получить новые необычные формы.
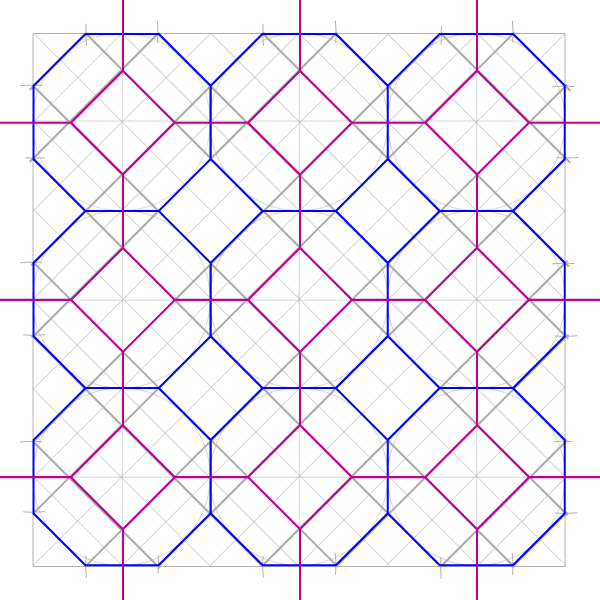
Но вернемся к нашему упражнению. С использованием восьмиугольных форм можно получить три различных простых узора на основе общей базовой структуры. Структура эта основана на четырех окружностях вокруг пятой, а, следовательно, образует сетку из квадратов, которая также носит название сетки пяти окружностей. Позвольте заметить, на случай если вам попадется термин, что структуры (сетки) на основе квадратов также носят название √2-сетки. Все эти термины значат, что мы работаем с числами 4 и 8 (и 12, и 16, и далее по мере прибавления 4).
При построении сетки невозможно переоценить важность очень точной работы, особенно теперь, когда от фигур мы переходим к узорам. Убедитесь, что карандаш как следует заточен и не спешите.
Видео:Построение недостающих проекции сквозного отверстия в сфереСкачать

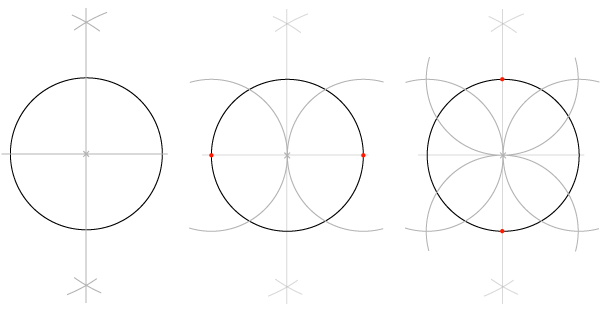
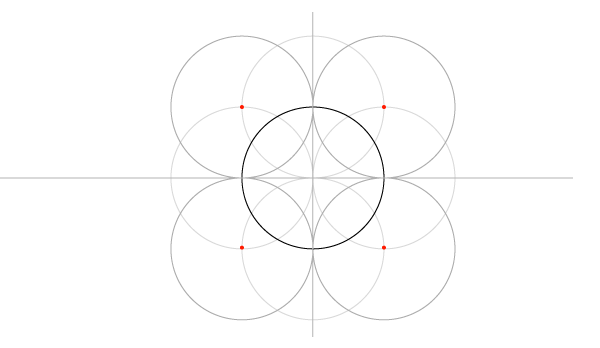
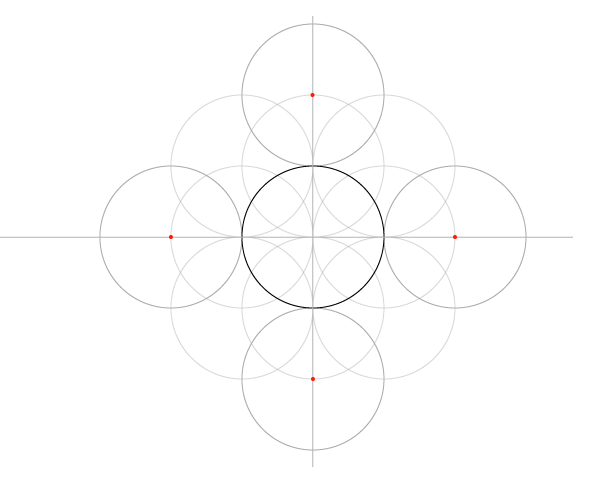
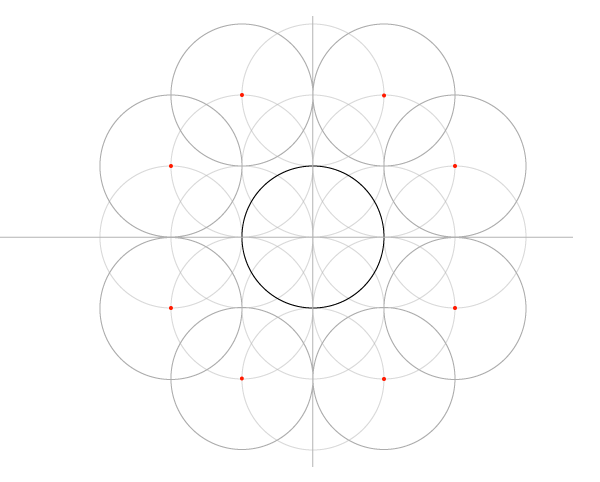
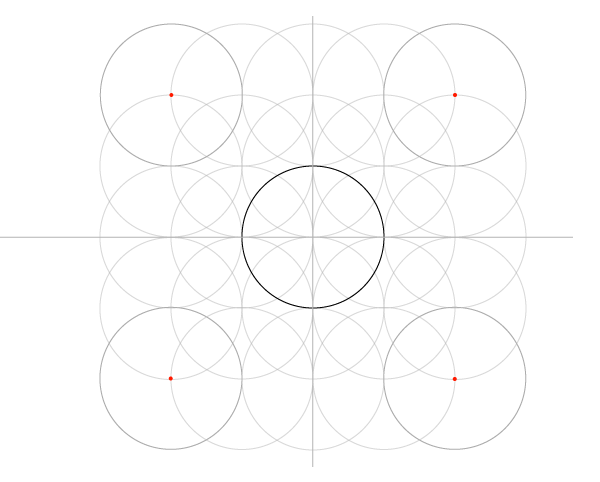
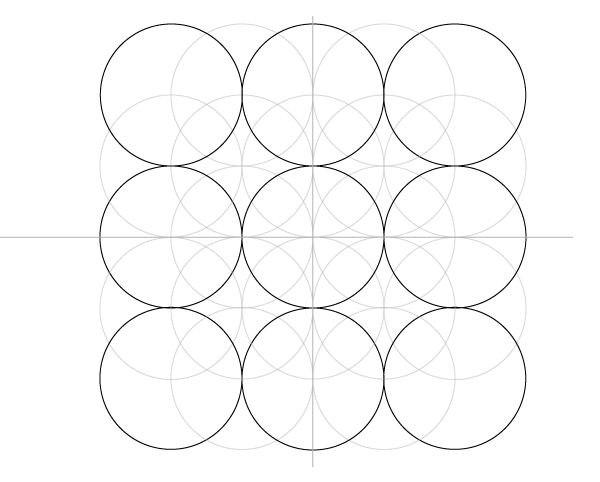
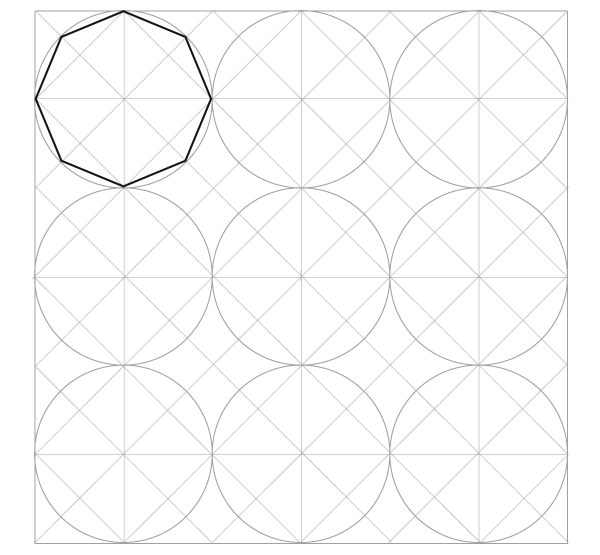
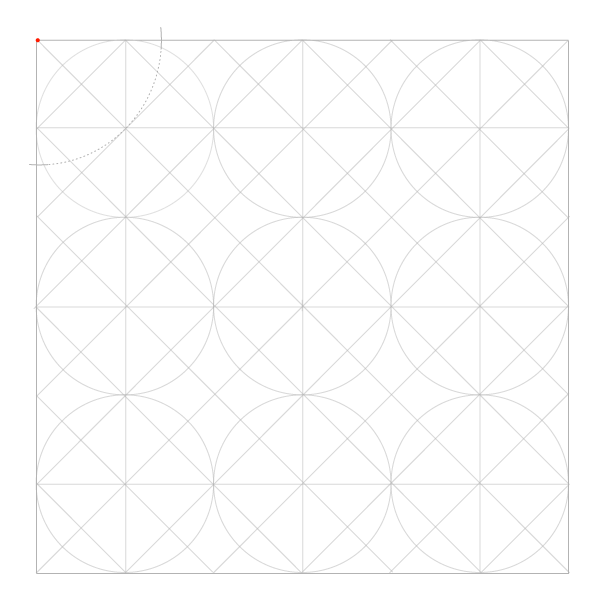
Сетка пяти окружностей
Шаг 1
Нарисуйте отрезок по горизонтали и окружность, центр которой лежит на этом отрезке, имея ввиду, что стороны квадратов в сетке равны диаметрам окружностей, и эта первая окружность будет центром сетки.
Шаг 2
Найдитеипостройтеперпендикуляр. Он должен быть как минимум равен отрезку, но может быть и длиннее.
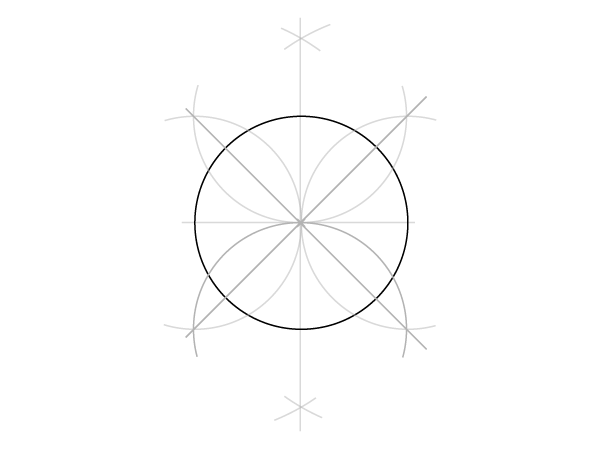
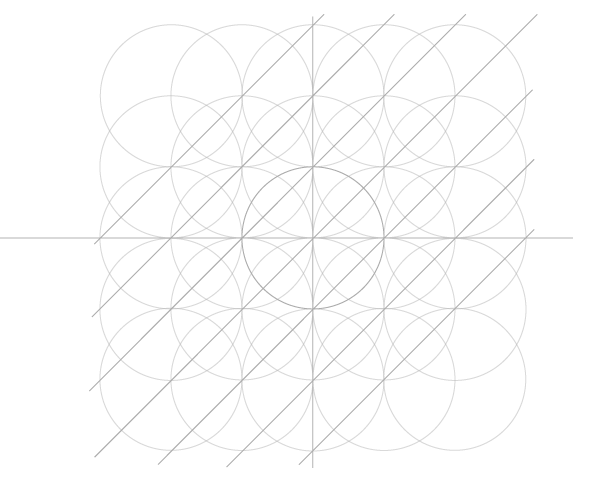
Шаги 3 и 4
Следующий шаг – знакомые нам дуги, только в этот раз рисуйте полные окружности. В итоге у нас должна получиться основа основ: пять окружностей, которые дали сетке имя.
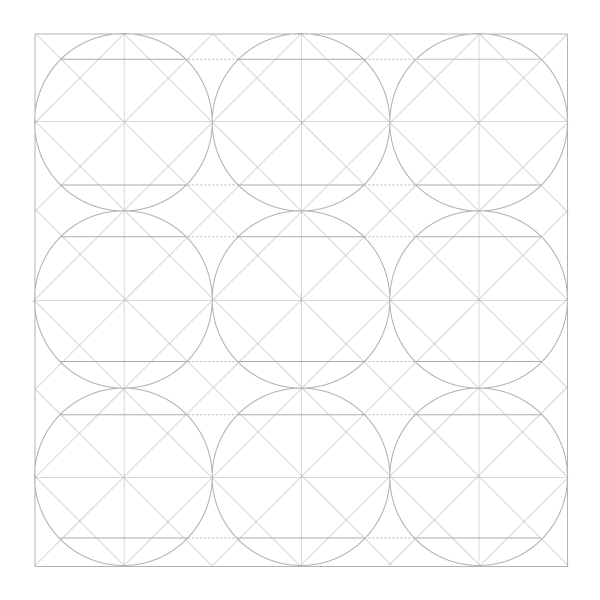
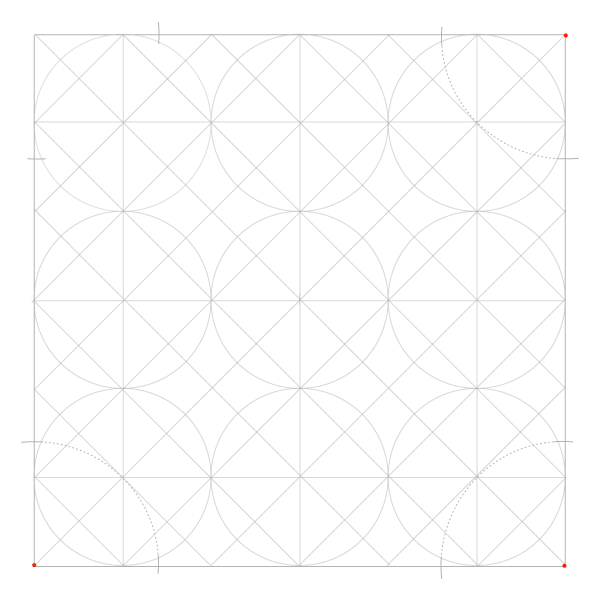
Шаг 5
Постройте еще 4 окружности с указанными на рисунке центрами…
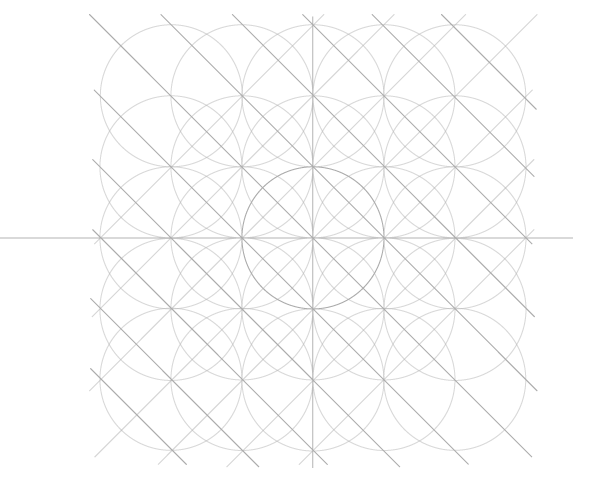
Шаг 6
Шаг 7
И еще восемь с центрами, указанными на рисунке ниже. Обратите внимание, что центры новых окружностей окажутся в точках пересечения предыдущих. Таким образом структуру можно расширять до бесконечности, но мы пока добавим только еще один блок.
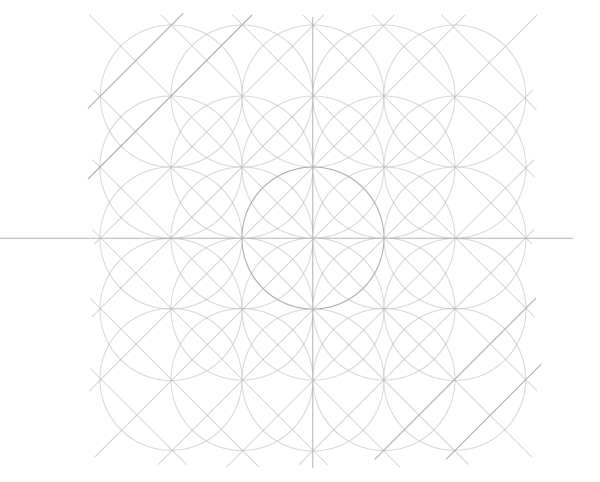
Шаг 8
Впишите стеку в квадрат, добавив окружности по углам.
Теперь у нас есть 25 окружностей, но большинство было нужно только чтобы построить сетку. Для начала работы над узором нам понадобится только 9 соприкасающихся окружностей, вписанные в соответствующие квадраты.
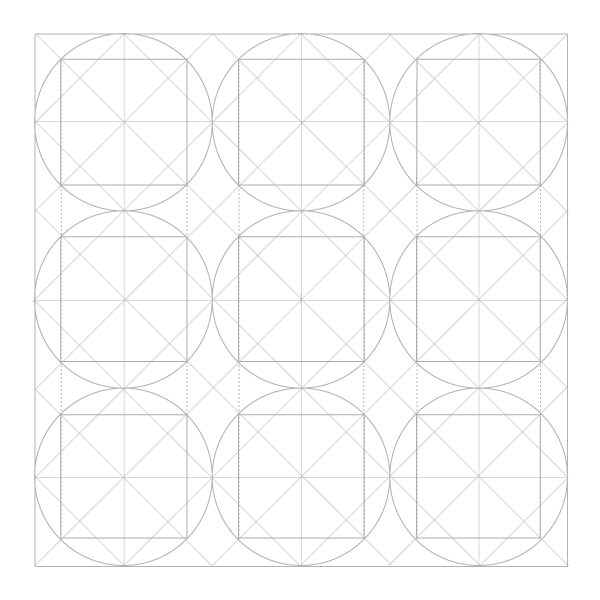
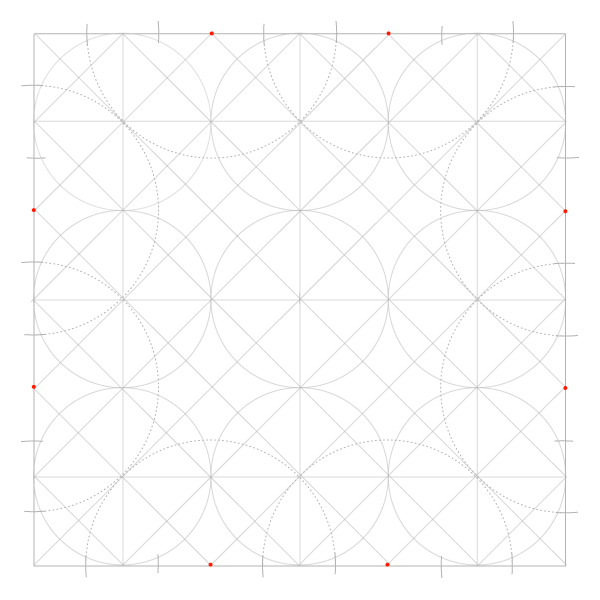
Шаг 9
Последний шаг в построении сетки – добавить диагонали. Углов у окружностей нет, но есть точки соприкосновения. Их и соединяем, сначала в одну сторону…
Добавляем недостающие соединением точек пересечения уже построенных диагоналей с окружностями по углам сетки.
Теперь перед нами сетка, которая ляжет в основу всех следующих построений. Можно еще построить квадрат, в который впишется сетка целиком, но это необязательно.
Видео:Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

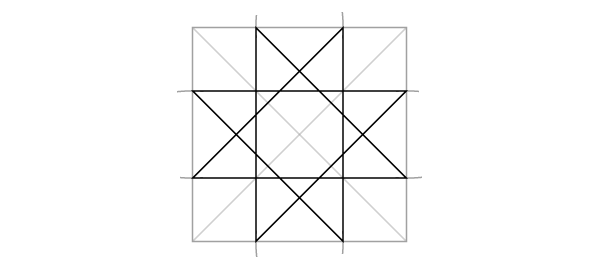
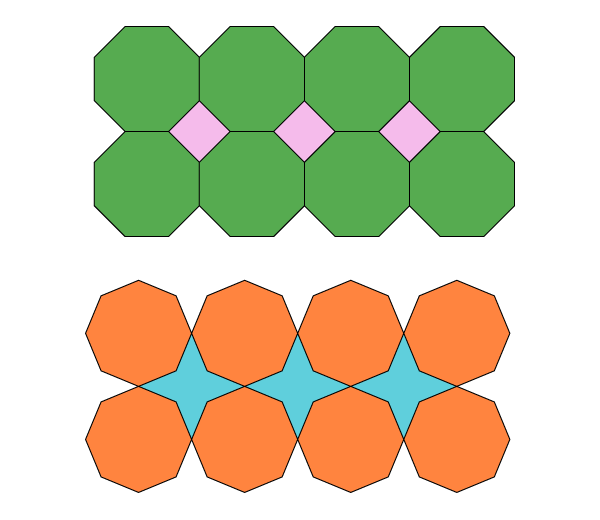
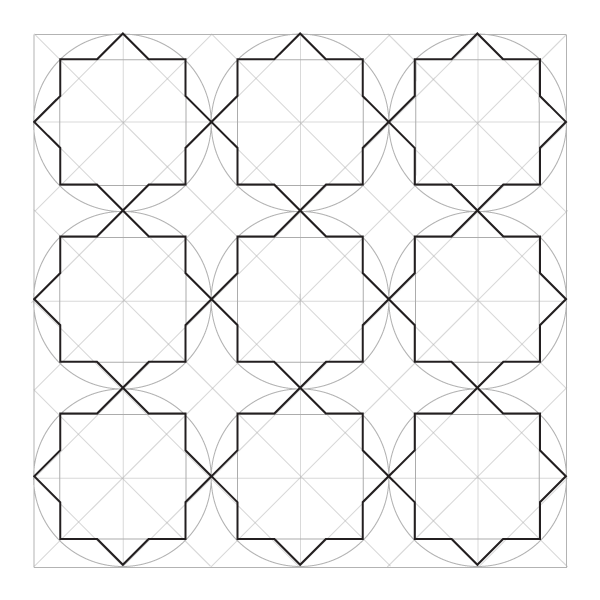
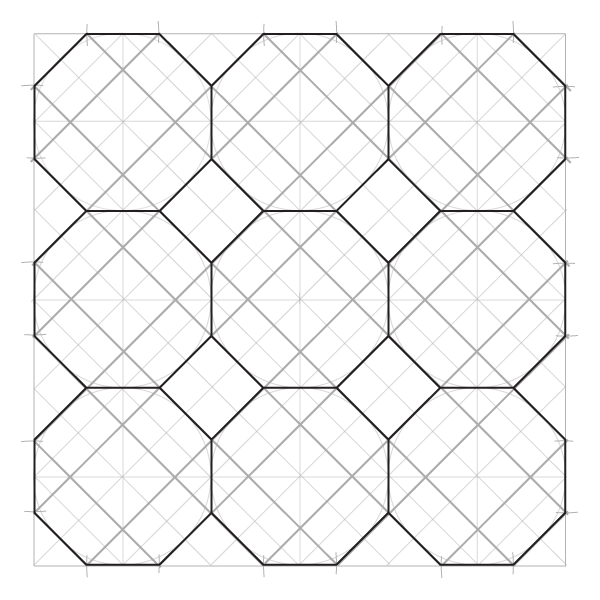
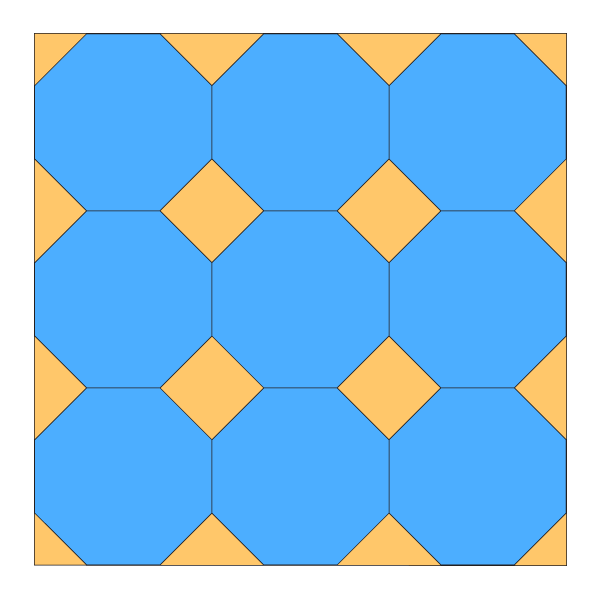
Узор из динамичных октагонов
Дополнительные построения не требуются: каждая окружность уже разделена на 8. Все, что от вас требуется, — соединить точки в каждой окружности.
Узорчатый пол в гробнице Итмад-Уд-Даулы, фото Дэвида Кастора (David Castor)
Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Дыхание милостивого
Это поэтическое название принадлежит узору, в котором октаграммы прилежат друг к другу, образуя крестообразные пустоты. Отправная точка снова сетка пяти окружностей.
Шаг 1
Динамичные квадраты уже есть – они образованы диагоналями. Добавляем горизонтальные стороны вторых квадратов…
Шаг 2
Шаг 3
Теперь обводим звезду, образованную наложением квадратов.
В том, что получилось, можно увидеть, откуда появилось название узора: октаграммы – “выдыхающие” квадраты (они расшираются), кресты – “вдыхающие” (они сжимаются).
Плитки из узора (развернутого на 45º), найденные в Иране, фотограф ean-Pierre Dalbéra.
Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Узор из статичных октагонов
Этот узор основан на статичных октагонах, которые мы уже научились строить немного раньше. Осталось только привязать наше умение к сетке. К счастью, нам нужно построить только самые удаленные от центра точки, все остальное сойдется само.
Шаг 1
Иглу циркуля устанавливаем в вершину внешнего квадрата и берем раскрыв, равный расстоянию от этой точки до центра ближайшей угловой окружности. Отмечаем на сторонах квадрата две точки.
Повторяем аналогичные построения для всех угловых окружностей и получаем еще 6 точек.
Продолжаем построения с иглой циркуля во внешних вершинах квадратов, образованных диагоналями.
Использование более мягкого карандаша позволит вам лучше понять, как новые линии ложатся на имеющуюся сетку: соедините им периферийные точки, которые вы только что наметили. Это новая сетка с новыми пересечениями.
Соедините эти пересечения, чтобы получить восьмиугольники, лежащие на одной стороне.
И напоследок: вот какой узор получится, если вы соедините лини, по которым октагоны накладываются друг на друга:
На сегодня все. Оперируя только числами 4 и 8 мы научились строить квадраты и октагоны, а также четырех- и восьмиконечные звезды, структуру на основе квадратов и 4 узора на основе этой структуры (а их можно придумать гораздо больше, чем 4).
В следующий раз все то же самое проделываем с числами 6 и 12.
Видео:2 2 3 построение изометрии окружностиСкачать

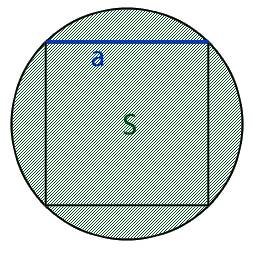
Квадрат вписанный в окружность
Видео:Параллельное проектирование и его свойства Изображение пространственных фигурСкачать

Определение
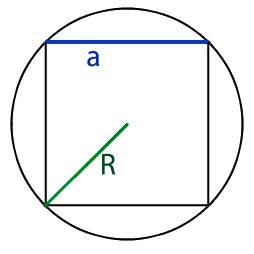
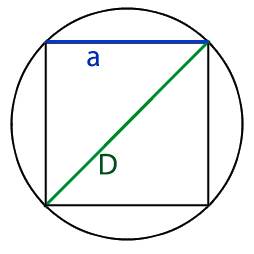
Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.
На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.
Видео:Построение правильного квадрата.Скачать

Формулы
Радиус вписанной окружности в квадрат
- Радиус вписанной окружности в квадрат, если известна сторона:
Радиус вписанной окружности в квадрат, если известен периметр:
Радиус вписанной окружности в квадрат, если известна площадь:
Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:
Радиус вписанной окружности в квадрат, если известна диагональ:
Радиус описанной окружности около квадрата
- Радиус описанной окружности около квадрата, если известна сторона:
Радиус описанной окружности около квадрата, если известен периметр:
Радиус описанной окружности около квадрата, если известнаплощадь:
Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:
Радиус описанной окружности около квадрата, если известнадиагональ:
Сторона квадрата
- Сторона квадрата вписанного в окружность, если известнаплощадь:
Сторона квадрата вписанного в окружность, если известнадиагональ:
Сторона квадрата вписанного в окружность, если известен периметр:
Площадь квадрата
- Площадь квадрата вписанного в окружность, если известна сторона:
Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:
Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:
Площадь квадрата вписанного в окружность, если известен периметр:
Площадь квадрата вписанного в окружность, если известна диагональ:
Периметр квадрата
- Периметр квадрата вписанного в окружность, если известна сторона:
Периметр квадрата вписанного в окружность, если известна площадь:
Периметр квадрата вписанного в окружность, если известенрадиус вписанной окружности:
Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:
Периметр квадрата вписанного в окружность, если известна диагональ:
Диагональ квадрата
- Диагональ квадрата вписанного в окружность, если известна сторона:
Диагональ квадрата вписанного в окружность, если известна площадь:
Диагональ квадрата вписанного в окружность, если известен периметр:
Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:
Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:
Видео:Построение 8 угольника циркулемСкачать

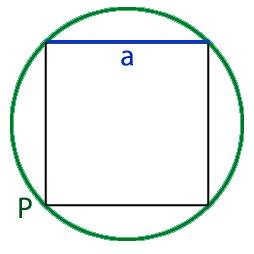
Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.
Для того что бы найти длину стороны вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
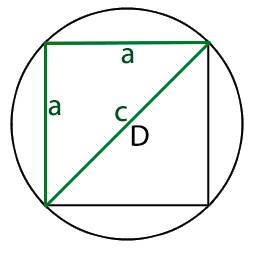
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
мы можем узнать длину сторон квадрата используя теорему Пифагора
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

ИЗОБРАЖЕНИЕ ВПИСАННЫХ И ОПИСАННЫХ ОКОЛО ОК-РУЖНОСТИ МНОГОУГОЛЬНИКОВ
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуляСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
ИЗОБРАЖЕНИЕ ВПИСАННЫХ И ОПИСАННЫХ ОКОЛО ОКРУЖНОСТИ МНОГОУГОЛЬНИКОВ
Задание: Дано изображение АВС произвольного треугольника А 1 В 1 С 1 , вписанного в окружность. Построить изображение высоты треугольника и биссектрисы, проведенных из вершины В 1 .
K 1 L 1 A 1 C 1 , OK 1 L 1 .
Соответственные построения проводим на изображении АВС треугольника А 1 В 1 С 1 , вписанного в окружность.
Задание: построить изображение касательной к окружности в точке А.
Строим эллипс с центром в точке О.
Проводим диаметр АВ и сопряженный ему диаметр DC .
Проводим АК DC
АК – искомая касательная.
Задание: построить изображение прямоугольного треугольника вписанного в окружность.
чертеж — оригинал изображение
В прямоугольном треугольнике центром описанной окружности является середина гипотенузы.
Задание: построить изображение равнобедренного треугольника.
чертеж — оригинал изображение
Для построения изображения равнобедренного треугольника достаточно построить два сопряженных диаметра. В случае остроугольного и тупоугольного равнобедренных треугольников строят хорду параллельную одному из сопряженных диаметров, которая послужит основанием треугольника. В случае, когда речь идет о прямоугольном равнобедренном треугольнике, один из сопряженных диаметров послужит основанием искомого треугольника.
Вершина искомого треугольника будет лежать на конце другого диаметра.
Задание: построить изображение правильного треугольника вписанного в окружность.
чертеж — оригинал изображение
Задание: построить изображение прямоугольника вписанного в окружность.
чертеж — оригинал изображение
Задание: построить изображение вписанной в окружность равнобокой трапеции.
чертеж – оригинал изображение
Задание: построить изображение квадрата вписанного в окружность.
чертеж – оригинал изображение
Задание: построить изображение правильного шестиугольника вписанного в окружность
Проведем ω(О; ОА 1 ), (А 1 А 4 ) ( MN ), О = (А 1 А 4 ) ( MN ), ОА 1 = R .
1.Строим эллипс (с центром О ).
2. Строим произвольный диаметр А′ 1 А′ 4 и сопряженный ему диаметр MN .
Задание: построить изображение описанного около окружности прямоугольного треугольника.
чертеж — оригинал изображение
Для построения изображения описанного около окружности прямоугольного треугольника используют тот факт, что его катеты это касательные к окружности в концах двух его сопряженных диаметров.
чертеж — оригинал изображение
Строим эллипс с центром в точке О и два сопряженных диаметра MN и KL .
Из точки В , лежащей на продолжении диаметра KL , проводим две касательные ( Р и Q – точки касания) до пересечения с прямой АС ( АС MN ).
Треугольник АВС является искомым равнобедренным треугольником.
Задание: построить изображение описанного около окружности равностороннего треугольника.
чертеж — оригинал изображение
Построение равностороннего треугольника аналогично построению равнобедренного треугольника. За исключением того, что здесь точку В выбирают не произвольно, а так, чтобы OL = LB .
Задание: построить изображение описанного около окружности квадрата.
чертеж — оригинал изображение
Стороны квадрата лежат на касательных к окружности, проходящих в концах сопряженных диаметром MN и KL . Точки касания делят стороны описанного квадрата пополам.
Задание: построить изображение ромба описанного около окружности.
чертеж — оригинал изображение
Диагоналям ромба АС и BD принадлежат сопряженные диаметры эллипса KL и MN соответственно. Одну из вершин ромба выбираем произвольно, например, вершину С . Из этой вершины проводим касательные отрезки. Например, отрезок CD касается эллипса в точке Р .
Замечание: точка Р не должна делить отрезок CD пополам, иначе, получим изображение описанного квадрата.
Задание: построить изображение описанной около окружности равнобокой трапеции.
чертеж — оригинал изображение
При построении изображения описанной около окружности равнобокой трапеции стоит учитывать, что диаметр K 1 L 1 перпендикулярен основаниям В 1 С 1 и А 1 D 1 и делит их пополам.
Строим касательные к эллипсу, проходящие через точки К и L , параллельные диаметру MN ( MN и KL сопряженные диаметры). Откладываем два равных отрезка КВ и КС , так чтобы КС был меньше ON . Через точки В и С проводим касательные к эллипсу. Точки пересечения этих касательных с касательной, проведенной в точке L , дают вершины A и D .
Второй способ:
Строим вписанную в окружность трапеции (см.выше). Затем проводим касательные к эллипсу параллельные сторонам трапеции. Точки пересечения касательных – вершимы искомой описанной равнобокой трапеции.
Задание: построить изображение описанного около окружности шестиугольника.
чертеж — оригинал изображение
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 944 человека из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 318 человек из 68 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 694 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 487 635 материалов в базе
Материал подходит для УМК
«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
88. Вписанный четырехугольник
Видео:Euclidea - 1. Альфа (Alpha) - 1.7 - Квадрат, вписанный в окружностьСкачать

Дистанционные курсы для педагогов
Другие материалы
- 04.05.2018
- 2847
- 04.05.2018
- 2940
- 04.05.2018
- 1750
- 04.05.2018
- 448
- 04.05.2018
- 490
- 04.05.2018
- 309
- 04.05.2018
- 500
- 04.05.2018
- 1826
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 06.05.2018 6301 —> —> —> —>
- DOCX 731 кбайт —> —>
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Голованова Елена Павловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 3 года и 11 месяцев
- Подписчики: 4
- Всего просмотров: 121484
- Всего материалов: 90
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
548 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Число иностранных студентов в РФ увеличилось за три года
Время чтения: 1 минута
Крупнейшие вузы Татарстана откроют цифровые кафедры в 2022 году
Время чтения: 1 минута
Регионы запустили работу по капремонту школ
Время чтения: 1 минута
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Петербурге дали рекомендации по переводу школьников на дистант
Время чтения: 3 минуты
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Квадрат вписанный в окружность
Определение
Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.
На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.
Формулы
Радиус вписанной окружности в квадрат
- Радиус вписанной окружности в квадрат, если известна сторона:
Радиус вписанной окружности в квадрат, если известен периметр:
Радиус вписанной окружности в квадрат, если известна площадь:
Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:
Радиус вписанной окружности в квадрат, если известна диагональ:
Радиус описанной окружности около квадрата
- Радиус описанной окружности около квадрата, если известна сторона:
Радиус описанной окружности около квадрата, если известен периметр:
Радиус описанной окружности около квадрата, если известнаплощадь:
Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:
Радиус описанной окружности около квадрата, если известнадиагональ:
Сторона квадрата
- Сторона квадрата вписанного в окружность, если известнаплощадь:
Сторона квадрата вписанного в окружность, если известнадиагональ:
Сторона квадрата вписанного в окружность, если известен периметр:
Площадь квадрата
- Площадь квадрата вписанного в окружность, если известна сторона:
Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:
Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:
Площадь квадрата вписанного в окружность, если известен периметр:
Площадь квадрата вписанного в окружность, если известна диагональ:
Периметр квадрата
- Периметр квадрата вписанного в окружность, если известна сторона:
Периметр квадрата вписанного в окружность, если известна площадь:
Периметр квадрата вписанного в окружность, если известенрадиус вписанной окружности:
Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:
Периметр квадрата вписанного в окружность, если известна диагональ:
Диагональ квадрата
- Диагональ квадрата вписанного в окружность, если известна сторона:
Диагональ квадрата вписанного в окружность, если известна площадь:
Диагональ квадрата вписанного в окружность, если известен периметр:
Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:
Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности: