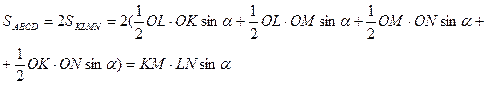Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла. Четырехугольник, у которого угол больше развернутого называется невыпуклым
Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
(Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)
- Сумма углов четырёхугольника равна 2 π = 360°.
- Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
- Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
- Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
- Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
- Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
- Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
Теорема Вариньона
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.
или сокращённо
Середины сторон произвольного четырёхугольника — вершины параллелограмма
Доказательство
Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников 
Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ 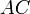
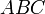
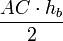
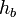
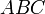
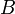
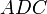
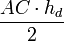
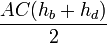
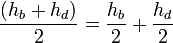
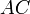
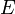
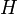
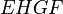
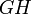
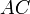
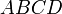
Теорема Эйлера
в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями
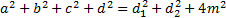

Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон
Теорема Птолемея
Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)
Если a, b, c, d – длины сторон четырёхугольника, 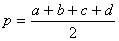
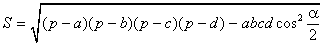
В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: 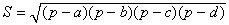
это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: 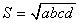
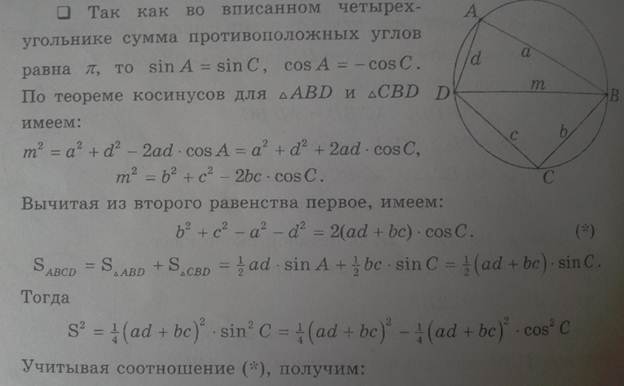
Видео:Теорема Эйлера для четырехугольника | Дополнительные главы школьной геометрииСкачать

Реферат: Бимедианы четырехугольника
| Название: Бимедианы четырехугольника Раздел: Рефераты по математике Тип: реферат Добавлен 13:27:38 12 июля 2011 Похожие работы Просмотров: 2012 Комментариев: 20 Оценило: 8 человек Средний балл: 5 Оценка: 5 Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
а) Так как диагонали исходного четырехугольника равны, то стороны параллелограмма Вариньона будут равны (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм Вариньона является ромбом (по признаку ромба).
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).
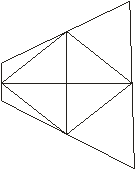
2. Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике:
а) диагонали перпендикулярны(см. рис. 3,а);
б) бимедианы равны(см. рис. 3,б).
|
|
а) Так как диагонали исходного четырехугольника перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Тогда параллелограмм Вариньона является прямоугольником (по признаку прямоугольника).
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).
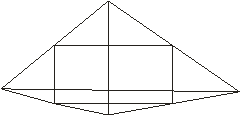
3. Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике:
а) диагонали равны и перпендикулярны(см. рис. 4,а);
б) бимедианы равны и перпендикулярны (см. рис. 4,б).
|
|
а) Так как диагонали исходного четырехугольника равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Тогда параллелограмм Вариньона является квадратом (по признаку квадрата).
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата).
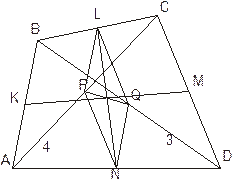
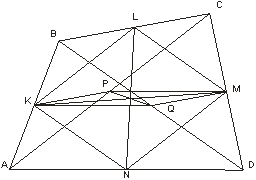
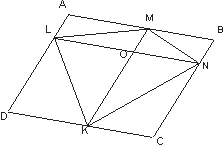
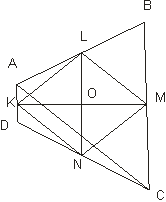
Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
Пусть KM и LN – бимедианы ABCD, PQ – отрезок, соединяющий середины диагоналей АС и BD.
То, что бимедианы KM и LN точкой пересечения делятся пополам, следует из того, что эти отрезки являются диагоналями параллелограмма Вариньона. Поэтому нам достаточно доказать, что отрезки PQ и LN их точкой пересечения делятся пополам (рис.5, а и б; обращаем внимание на то, что в невыпуклом четырехугольнике одна из диагоналей расположена вне четырехугольника).
|
|
Используя теорему о средней линии треугольника для соответствующих треугольников, имеем:
Тем самым, PLQN – параллелограмм. По свойству параллелограмма следует, что отрезки PQ и LN их точкой пересечения делятся пополам. Что и требовалось доказать.
1.3.3. Следствие 3.(теорема Эйлера).
Для четырехугольника сумма квадратов всех сторон равна сумме квадратов диагоналей плюс учетверенный квадрат отрезка, соединяющего середины диагоналей, то есть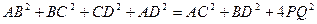
|
Уже было отмечено что LPNQ – параллелограмм (рис.6).
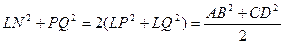
В последнем равенстве мы дважды воспользовались теоремой о средней линии треугольника. Аналогично для параллелограмма KPMQ имеем:
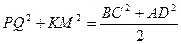
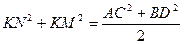
Так как KLMN – параллелограмм Вариньона четырехугольника ABCD . Складывая первые два равенства и учитывая последнее, получаем соотношение Эйлера.
1.3.4.Следствие 4.(теорема о бабочках).
Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны (рис. 7 ).
|
Воспользуемся теоремой о средней линии треугольника. Получаем:
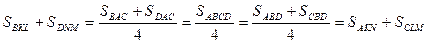
Что и требовалось доказать.
2.1.задачи из школьного курса геометрии.
Рассмотрим задачи на бимедианы четырехугольника и теорему Вариньона, которые встречаются в школьном курсе геометрии.
Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.
а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (см.следствие 1, 1, а);
Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (см. следствие 1, 1, б).
б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 1, 2, а);
Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 1, 2, б).
У четырехугольника диагонали равны a и b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Периметр параллелограмма Вариньона равен a+ b .
Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.
См. теорему Вариньона.
2.2. Конкурсные задачи.
Рассмотрим задачи на бимедианы четырехугольника и теорему Вариньона, которые взяты нами с различных математических конкурсов и олимпиад.
Пусть K, L, M, N – середины сторон выпуклого четырехугольника ABCD (см. рис. 8). Докажите, что
а) 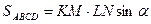
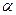
б) 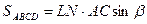
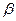
|
а) Так как ABCD — параллелограмм Вариньона, а KMи NL– бимедианы, то 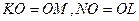
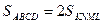
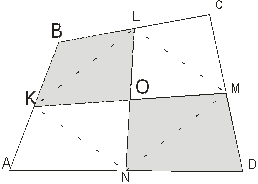
Докажите, что площадь параллелограмма, образованного прямыми, проходящими через вершины выпуклого четырехугольника и параллельными его диагоналям, в два раза больше площади исходного четырехугольника (рис.9).
|
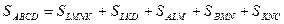
Так как AMOL, MONB, CKON, DKOL — параллелограммы, то 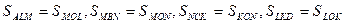
Отсюда получаем, что 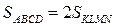
Все стороны выпуклого четырехугольника площади 1 разделены на 2n равных частей, а затем точки деления на противоположных сторонах соединены так, чтобы получилась «косоугольная шахматная доска», состоящая из белых и черных «клеток» (см. рис. при n= 2). Доказать, что сумма площадей всех белых «клеток» равна сумме площадей всех черных «клеток» (рис.10).
|
Из следствия 2 следует, что точки пересечения отрезков на этой доске делят каждый на равные части.
Тогда в любом «маленьком» четырехугольнике (рис.10),куда входят ровно две белые и две черные клетки, выполняются условия теоремы о бабочках. Нужное равенство установлено.
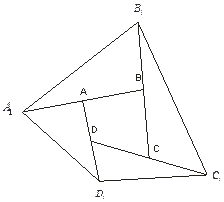
На продолжениях сторон выпуклого четырехугольника ABCD выбраны точки 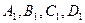
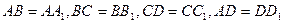
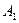
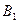
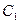
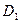
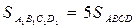
|
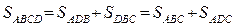
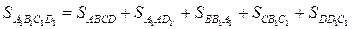
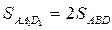
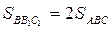
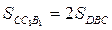
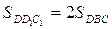
Отсюда получаем, что 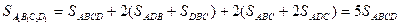
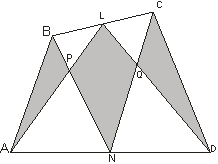
Пусть L и N – середины противоположных сторон BC и AD четырехугольника ABCD (рис. 12). Доказать, что площадь четырехугольника LPNQ равна сумме площадей треугольников ABP и CQD .
|
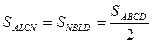
В треугольникеACD медиана CN делит его на два треугольника равной площади, а в треугольнике ABC медиана AL делит его на два равновеликих треугольника. Так как 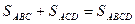
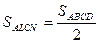
Теперь утверждение задачи следует из того, что четырехугольники ALCN и NBLD покрывают внутри четырехугольника ABCD два раза четырехугольник LPNQ и не покрывают треугольники ABP иCQD , а их сумма их площадей равна площади четырехугольника ABCD. Площадь четырехугольника, с другой стороны, равна сумме площадей шести треугольников (в том числе и треугольников ABP и CQD ) и интересующего нас четырехугольника LPNQ .
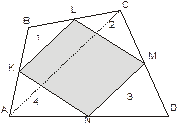
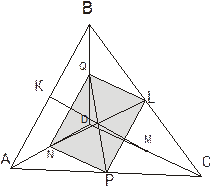
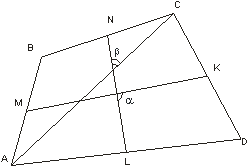
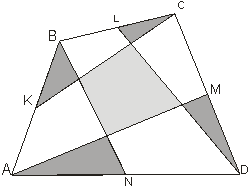
Пусть K, L, M, N – середины сторон (рис. 13) выпуклого четырехугольника ABCD . Докажите, что площадь четырехугольника, образованного прямыми CK, AM, BN, DL, равна сумме площадей четырех треугольников, отмеченных на рисунке 6.
|
Так как 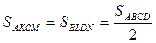
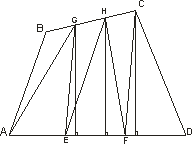
Противоположные стороны четырехугольника ABCD разделены на три равные части и точки деления попарно соединены (рис.14). Доказать, что одна из площадей получившихся трех четырехугольников равна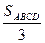
|
Докажем, что площадь среднего четырехугольника равна трети площади исходного четырехугольника. Другими словами докажем, что
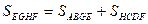
Чтобы в этом убедиться, достаточно проверить, что
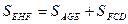
А последнее равенство есть следствие того, что основания AE, EF, FD всех трех треугольников в этом равенстве равны, а высота треугольника EHF является средней линией трапеции с основаниями, равными высотам треугольников AGE и FCD.
Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника ABCD ,перпендикулярны (Рис.15) . Известно, что

Найдите площадь четырехугольника ABCD и сравните её с числом 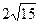
|
Так как бимедианы перпендикулярны, то параллелограмм Вариньона является ромбом (см.следствие1,1,б).
Так как KN является средней линией треугольника ADC , то по теореме о средней линии треугольника KN=0,5 AC=2 ;
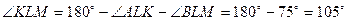
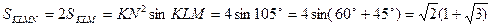
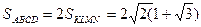
Площадь ABCD меньше, чем 2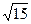
Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника ABCD ,перпендикулярны (Рис.15) . Известно, что
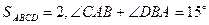
Найдите квадрат длины отрезка PR и сравните его с числом 4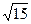
Пусть KLMN – параллелограмм Вариньона четырехугольника ABCD .
Так как бимедианы перпендикулярны, то параллелограмм Вариньона является ромбом (см. следствие1,1,б).
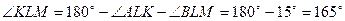
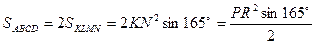
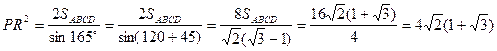
1. Погорелов А. В. Геометрия: Учеб. для 7 – 11 кл. сред. шк.- М.: Просвещение,1990.- 384 с.
2. Штейнгауз Г.Математический калейдоскоп. – М.:наука,1981.
3. Прасолов В.В. задачи по планиметрии. – Т.1, 2. – М.: Наука,1995.
4. Коксетер Г. С. М., Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука,1978.
5. В. Вавилов, П. Красников. Бимедианы четырехугольника//Математика. 2006 — №22.
Видео:Малая теорема Ферма и теорема Эйлера | Ботай со мной #037 | Борис Трушин !Скачать

Различные доказательства теоремы Эйлера.
Современная теория многогранников берет свое начало с работ Леонарда Эйлера (1707-1783) – одного из величайших математиков мира, работы которого оказали решающее влияние на развитие многих разделов математики. Л. Эйлер был не только выдающимся математиком, но и крупной творческой личностью. Им было написано около 760 научных статей для журналов, 40 книг, 15 работ для различных конкурсов. Поражает работоспособность ученого, росшая на протяжении всей жизни. Так, в первые 14 лет научной деятельности им было написано 80 работ объемом около 4000 печатных листов, а в последние 14 лет жизни, несмотря на тяжелую болезнь – слепоту, опубликовано свыше 359 работ общим объемом приблизительно 8000 печатных листов. Многие рукописи Эйлера сохранились до наших дней. Эйлер долгое время (с 1727 по 1741 год и с 1766 до конца жизни) жил и работал в России, был действительным членом Петербургской академии наук, оказал большое влияние на развитие русской математической школы, на подготовку кадров ученых – математиков и педагогов России.
Работы Эйлера дали толчок к постановке и решению различных проблем, способствовали развитию многих разделов математики. Математики последующих поколений учились у Эйлера. Например, французский ученый П. С. Лаплас говорил: «Читайте Эйлера, он учитель всех нас».
В 1752 году Эйлером была доказана ставшая знаменитой теорема о числе граней, вершин и ребер выпуклого многогранника. Она была помещена в работе «Доказательство некоторых замечательных свойств, которым подчинены тела, ограниченные плоскими гранями».
Рассмотрим различные доказательства этой теоремы. В дальнейшем данный материал можно использовать как для факультативных и кружковых занятий, так и для самостоятельного изучения учениками.
Прежде чем рассматривать доказательство, обратимся к следующей таблице (Г- число граней многогранника, В – вершин, Р — ребер ):
| Название многогранника | Г | В | Р |
| Тетраэдр | 4 | 4 | 6 |
| Четырехугольная призма | 6 | 8 | 12 |
| Семиугольная пирамида | 8 | 8 | 14 |
| Пятиугольная бипирамида | 10 | 7 | 15 |
| Правильный додекаэдр | 12 | 20 | 30 |
Теперь найдем сумму Г+В-Р для каждого из представленных в таблице многогранников. Во всех случаях получилось: Г+В-Р=2. Справедливо это только для выбранных многогранников? Оказывается это соотношение справедливо для произвольного выпуклого многогранника. Это свойство впервые было подмечено и затем доказано Л. Эйлером.
Теорема Эйлера. Для любого выпуклого многогранника справедливо соотношение Г+В-Р=2 (*), где Г – число граней, В – число вершин и Р – число ребер данного многогранника.
Доказательство. Существует множество различных доказательств теоремы Эйлера. Предлагается рассмотреть три наиболее интересных из них.
1) 
Представим поверхность данного многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность «растянем» на плоскость. Тогда на плоскости получается сетка (рис 3), содержащая Г′=Г-1 областей (которые по-прежнему назовем гранями), В вершин и Р ребер (которые могут искривляться).
Для данной сетки нужно доказать соотношение
тогда для многогранника будет справедливо соотношение (*).
Докажем, что соотношение (**) не меняется, если в сетке провести какую-либо диагональ. Действительно, после проведения некоторой диагонали в сетке будет Г′+1 граней, В вершин и Р+1 ребро, т.е.
Пользуясь этим свойством, проведем в сетке диагонали, разбивающие ее на треугольники (на рисунке 3 диагонали изображены пунктирами), и докажем соотношение (**) методом математической индукции по числу n треугольников в сетке.
Пусть n=1, т.е. сетка состоит из одного треугольника. Тогда Г′=1, В=3, Р=3 и выполняется соотношение(**). Пусть теперь соотношение (**) имеет место для сетки, состоящей из n треугольников. Присоединим к ней еще один треугольник. Его можно присоединить следующими способами:
1. как ∆ABC (рис 3). Тогда сетка состоит из Г′+1 граней, В+1 вершин и Р+2 ребер, и, следовательно,
2. Как ∆MNL. Тогда сетка состоит из Г′+1 граней, В вершин и Р+1 ребер, и, следовательно,
Таким образом, в обоих случаях, т.е. при любом присоединении (n+1)-го треугольника, выражение (**) не меняется, и если оно равнялось 1 для сетки из n треугольников, то оно равняется 1 и для сетки из (n+1) треугольника. Итак, соотношение (**) имеет место для любой сетки из треугольников, значит, для любой сетки вообще. Следовательно, для данного многогранника справедливо соотношение (*). Такое доказательство предложено в [18].
2)Способ доказательства теоремы Эйлера, связанный с нахождением суммы плоских углов выпуклого многогранника. Обозначим ее ∑а. Напомним, что плоским углом многогранника являются внутренние плоские углы его граней.
Например, найдем ∑а для таких многогранников:
а) тетраэдр имеет 4 грани – все треугольники. Таким образом, ∑а 
б) куб имеет 6 граней – все квадраты. Таким образом, ∑а = 6∙π = 12π;
в) возьмем теперь произвольную пятиугольную призму. У нее две грани – пятиугольники и пять граней – параллелограммы. Сумма углов выпуклого пятиугольника равна 3π. (Напомним, что сумма внутренних углов выпуклого n-угольника равна π (n-2).) Сумма углов параллелограмма равна 2π. Таким образом,
Итак, для нахождения ∑а мы вычисляли сначала сумму углов, принадлежащих каждой грани. Воспользуемся этим приемом и в общем случае.
Введем следующие обозначения: S1, S2, S3, …, Sr – число сторон 1, 2, 3-й и т.д. последней грани многогранника. Тогда
Далее найдем общее число сторон всех граней многогранника. Оно равно S1 +S2 +S3 +…+Sr . Так как каждое ребро многогранника принадлежит двум граням, имеем:

Сосчитаем теперь ∑а другим способом. Для этого будем менять форму многогранника таким образом, чтобы у него не менялось число Г, В и Р. При этом может измениться каждый плоский угол в отдельности, но число ∑а останется прежним. Выберем такое преобразование многогранника: примем одну из его граней за основание, расположим его горизонтально и «растянем» для того, чтобы на него можно было спроектировать Другие грани многогранника. Например, на рисунке 4.а показано, к чему мы придем в случае тетраэдра, а на рисунке 4.б – в случае куба. На рисунке 5 показан многогранник произвольного типа.

1) Сумма углов нижней грани, у которой r сторон, равна π (r-2).
2) Сумма углов верхней пластины, вершинами которых являются вершины нижней грани, тоже равна π (r-2).
3) Сумма «внутренних» углов верхней пластины равна 2π (В-r), так как верхняя пластина имеет (В-r) внутренних вершин и все углы группируются около них. Итак,
∑а = π (r-2) + π (r-2) + 2π (В-r) = 2πВ — 4π. (2)
Таким образом, сравнивая выражения (1) и (2), получаем:
что и требовалось доказать.
Этот способ доказательства теоремы Эйлера рассмотрен в книге американского математика и педагога Джорджа Пойа. [10]
3)Способ, предложенный математиком Л.Н. Бескиным. [5]
Здесь, как и в случае 1), вырезаем одну грань многогранника и оставшуюся поверхность растягиваем на плоскость. При этом на плоскости получается некоторая плоская фигура, например, изображенная на рисунке 6.
Представим себе, что эта плоская фигура изображает собой остров, который со всех сторон окружен морем и состоит из отдельных полей – граней, отделенных друг от друга и от воды плотинами – ребрами.
Начнем постепенно снимать плотины, чтобы вода попала на поля. Причем плотину можно снять только в том случае, если она граничит с водой лишь с одной стороны. Снимая очередную плотину, мы орошаем ровно одно поле. Покажем теперь, что число всех плотин (т.е. Р – число ребер взятого многогранника) равно сумме чисел снятых и оставшихся плотин.

🔥 Видео
Теорема Эйлера | Доказательство.Скачать

Математика для всех. Алексей Савватеев. Лекция 2.4. Теорема ЭйлераСкачать

Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

10 класс, 29 урок, Теорема ЭйлераСкачать

#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать

Теоремы Эйлера и Ферма + задача с древнего IMO | Олимпиадная математикаСкачать

✓ Формула Эйлера для графов и многогранников за 8 минут | Ботай со мной #103 | Борис ТрушинСкачать

Функция Эйлера | Теория чиселСкачать

Функция ЭйлераСкачать

Задачи на доказательство делимости. Малая теорема Ферма | Ботай со мной #036 | Борис Трушин !Скачать

Гипотеза Пуанкаре — Алексей Савватеев на ПостНаукеСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

06. Формула ЭйлераСкачать

Формула Эйлера: объяснение | Самая красивая формула математики – Алексей Савватеев | ЛекцииСкачать

Остаток от деления 14^245 на 90 | Теорема Эйлера | Теория чисел | КАК РЕШАТЬ?Скачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Великая теорема ФермаСкачать

Прямая Эйлера (доказательство)Скачать