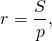Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Видео:Вписанная окружностьСкачать

Вписанная окружность
Что такое вписанная окружность?Какими свойствами она обладает?
Вписанная в выпуклый многоугольник окружность — это окружность, которая касается всех сторон этого многоугольника (то есть каждая из сторон многоугольника является для окружности касательной).
Центр вписанной окружности лежит внутри многоугольника.
Многоугольник, в который вписана окружность, называется описанным.
В выпуклый многоугольник можно вписать окружность, если биссектрисы всех его внутренних углов пересекаются в одной точке.
Центр вписанной в многоугольник окружности — точка пересечения его биссектрис.
Центр вписанной окружности равноудален от сторон многоугольника. Расстояние от центра до любой стороны равно радиусу вписанной окружности (По свойству касательной, сторона описанного многоугольника перпендикулярна радиусу, проведённому в точку касания).
По свойству касательных, проведённых из одной точки, любая вершина описанного многоугольника равноудалена от точек касания, лежащих на сторонах, выходящих из этой вершины.

ABCDE — описанный пятиугольник.
O — точка пересечения биссектрис ABCD, то есть ∠EAO=∠BAO, ∠ABO=∠CBO, ∠BCO=∠DCO, ∠CDO=∠EDO, ∠AEO=∠DEO.

Вершины ABCDE равноудалены от соответствующих точек касания:
AM=AN, BN=BL, CL=CK, DK=DP, EP=EM.
В любой треугольник можно вписать окружность. Центр вписанной в треугольник окружности называется инцентром.
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. В частности, в трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон.
В любой правильный многоугольник можно вписать окружность. Около любого правильного многоугольника можно также описать окружность. Центр вписанной и описанной окружностей лежат в центре правильного многоугольника.
Для любого описанного многоугольника радиус вписанной окружности может быть найден по формуле
где S — площадь многоугольника, p — его полупериметр.
Кроме основной, существуют формулы для нахождения радиуса вписанной окружности в частных случаях (для правильных многоугольников, отдельных видов треугольников, трапеции, ромба и т.д.).
Видео:8 класс, 38 урок, Вписанная окружностьСкачать

Вписанная окружность
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность. На рисунке 1 четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
Теорема
| В любой треугольник можно вписать окружность. |
Доказательство
Дано: произвольный 
Доказать: в 
Доказательство:
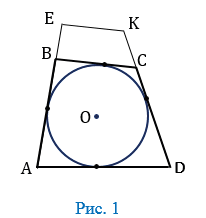
1. Проведем биссектрисы углов А, В и С, которые пересекутся в точке О (следствие из свойства биссектрис). Из точки О проведем перпендикуляры ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА (Рис. 2).
2. Точка О равноудалена от сторон 


Замечание 1
| В треугольник можно вписать только одну окружность. |
Доказательство
Предположим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают, значит в треугольник можно вписать только одну окружность. Что и требовалось доказать.
Замечание 2
| Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности. |
Доказательство
На рисунке 2 мы видим, что 
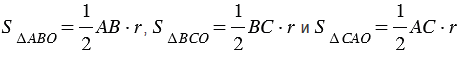

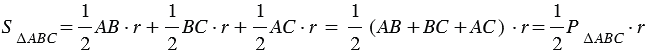
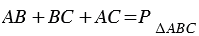

Замечание 3
| Не во всякий четырехугольник можно вписать окружность. |
Доказательство
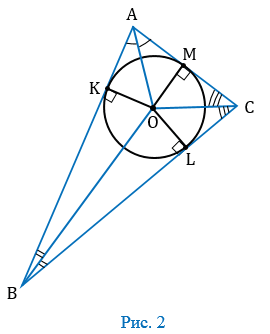
Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т.е. прямоугольник, не являющийся квадратом. В такой прямоугольник можно «поместить» окружность, касающуюся трех его сторон (Рис.3), но нельзя «поместить» окружность так, чтобы она касалась всех четырех его сторон, т.к. диаметр окружности меньше большей стороны прямоугольника т.е. нельзя вписать окружность. Что и требовалось доказать.
Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
| В любом описанном четырехугольнике суммы противоположных сторон равны. |
Доказательство
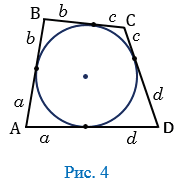
Рассмотрим четырехугольник АВСD, описанный около окружности (Рис. 4).
На рисунке 4 одинаковыми буквами обозначены равные отрезки касательных, т.к. отрезки касательных к окружности, проведенные из одной точки, равны. Тогда АВ + СD = 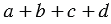
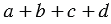
Верно и обратное утверждение:
| Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. |
Доказательство
Пусть в выпуклом четырехугольнике АВСD
АВ + СD = ВС + АD. (1)
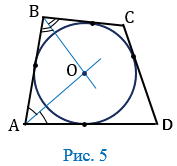
Точка О пересечения биссектрис углов А и В равноудалена от сторон АD, АВ и ВС (свойство биссектрис), поэтому можно провести окружность с центром О, касающуюся указанных трех сторон (Рис. 5).
Докажем, что эта окружность касается также стороны СD и, значит, является вписанной в четырехугольник АВСD.
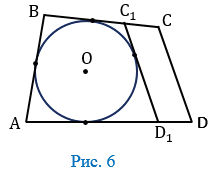
Предположим, что это не так. Тогда прямая СD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай (Рис. 6). Проведем касательную С1D1, параллельную стороне СD (С1 и D1 — точки пересечения касательной со сторонами ВС и АD).
Так как АВС1D1 — описанный четырехугольник, то по свойству его противоположных сторон
АВ + С1D1 = ВС1 + AD1. (2)
Но ВС1 = ВС — С1С, АD1 = АD — D1D, поэтому из равенства (2) получаем:
С1D1 + С1С + D1D = ВС + АD — АВ.
Правая часть этого равенства в силу (1) равна СD. Следовательно, приходим к равенству
т.е. в четырехугольник С1СDD1 одна сторона равна сумме трех других сторон. Но этого не может быть, т.к. к аждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон. Значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны СD. Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
🎬 Видео
Вписанная окружность | Геометрия 7-9 класс #74 | ИнфоурокСкачать

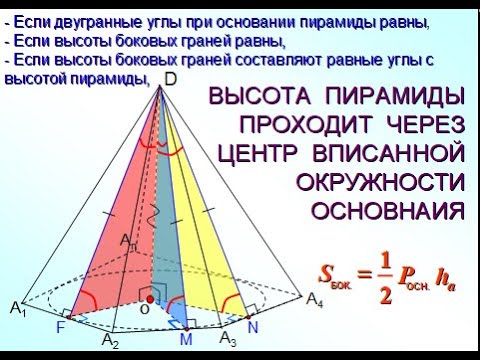
Пирамиды, в которых высота проходит через центр вписанной в основание окружностиСкачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

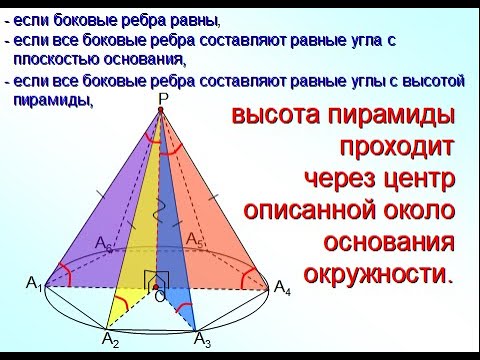
Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать
Вписанная окружность. Доказательства свойствСкачать

✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

Центр вписанной окружности #ShortsСкачать

Описанная и вписанная окружности треугольникаСкачать

Центр вписанной окружности.Скачать

Окружность, вписанная в треугольникСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Описанная и вписанная окружности треугольникаСкачать

Вписанная окружностьСкачать

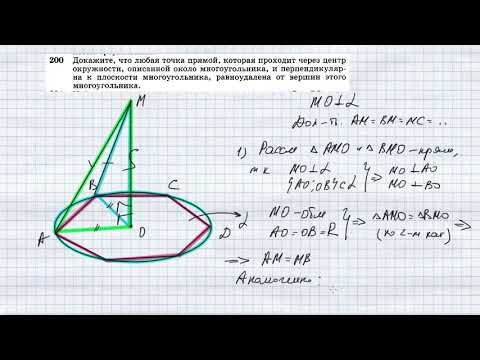
№200. Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около мноСкачать
Вторая замечательная точка треугольникаСкачать

Вписанные и описанные окружности (в треугольник)Скачать

Вписанная окружность. Видеоурок по геометрии 8 классСкачать