Геометрия | 10 — 11 классы
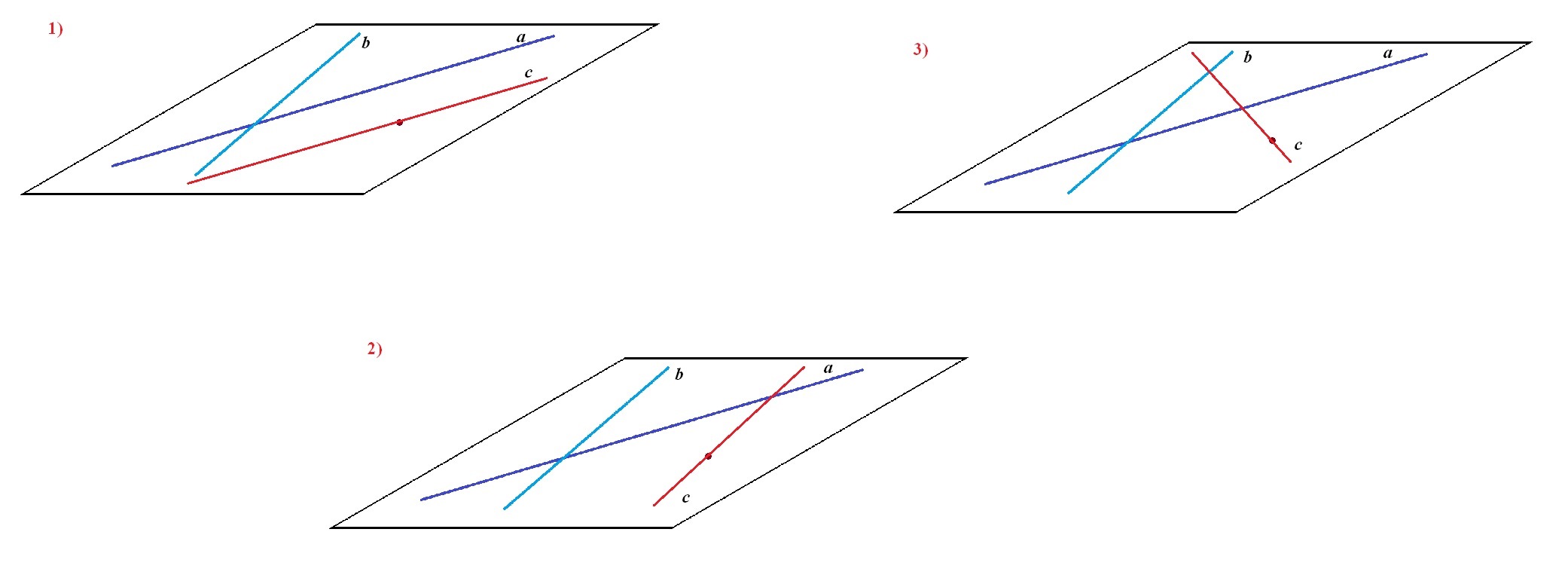
В плоскости двух пересекающихся прямых a и b задана точка С, не принадлежащая этим прямым.
Прямая с, лежащая в данной плоскости, проходит через точку С.
Как может быть расположена прямая с относительно данных прямых?
При таком условии возможны 3 случая расположения прямой с в плоскости пересекающихся прямых a и b.
3) с пересекает обе прямые а и b.
- Помогите пожалуйстаааа, срочно( Дано : плоскость альфа параллельна плоскости бетта, прямая А пересекает прямую В в точке О?
- Изобразите прямую l, лежащую в плоскости у, точки М и К, принадлежащие прямой L, и точку N, не пренадлежащую плоскости у?
- Ответьте, пожалуйста, на вопросы :1?
- Помогите пожалуйста)) 1?
- Плоскости Альфа и Бета пересекаются по прямой «а» ; прямая «b», лежащая в плоскости Бета, пересекает Альфа в точке А?
- Можно ли через точку пересечения двух данных прямых провести третью прямую не лежащую с ними в одной плоскости?
- Даны прямая и точка, не лежащая на этой прямой?
- Прямая а || в?
- 1. ДАНА ПРЯМАЯ?
- Даны прямая и точка, не лежащая на этой прямой?
- Контрольная работа №2 Вариант 1 Вплоскости двух параллельных прямых a и b дана точка C, не принадлежащая этим прямым. Через нее проведена прямая c. Найдите все возможные расположения прямой
- Главная > Документ
- Контрольная работа № 1
- Вариант 1
- Вариант 2
- Контрольная работа № 2
- Вариант 1
- Вариант 2
- Контрольная работа № 3
- Вариант 1
- Вариант 2
- Контрольная работа № 4
- Вариант 1
- Вариант 2
- Контрольная работа № 5
- Вариант 1
- Вариант 2
- Контрольная работа № 6
- Вариант 1
- Вариант 2
- Контрольная работа № 1
- Вариант 1
- Вариант 2
- Контрольная работа № 2
- Вариант 1
- Контрольная работа № 3
- Вариант 1
- Вариант 2
- Контрольная работа № 4
- Вариант 1
- Вариант 2
- Контрольная работа № 5
- Вариант 1
- Вариант 2
- Вариант 2
- Контрольная работа № 5
- Вариант 1
- Самостоятельные работы (стр. 1 )
Видео:№61. Даны пересекающиеся прямые а и b и точка А, не лежащая в плоскости этих прямых.Скачать

Помогите пожалуйстаааа, срочно( Дано : плоскость альфа параллельна плоскости бетта, прямая А пересекает прямую В в точке О?
Помогите пожалуйстаааа, срочно( Дано : плоскость альфа параллельна плоскости бетта, прямая А пересекает прямую В в точке О.
Прямая А пересекает плоскость альфа в точке В, прямая А пересекает плоскость бетта в точке D, прямая В пересекает плоскость льфа в точке А, прямая В пересекает плоскость бетта в точке С, АО = ОС, DО = ОВ.
Определить вид четырехугольника.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Изобразите прямую l, лежащую в плоскости у, точки М и К, принадлежащие прямой L, и точку N, не пренадлежащую плоскости у?
Изобразите прямую l, лежащую в плоскости у, точки М и К, принадлежащие прямой L, и точку N, не пренадлежащую плоскости у.
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Ответьте, пожалуйста, на вопросы :1?
Ответьте, пожалуйста, на вопросы :
Верно ли что если три данные точки лежат в каждой из двух различных плоскостей, то они лежат на одной плоскости?
2. Плоскости КДМ и СМК пересекаются по прямой В.
Назовите две точки, лежащие на прямой В 3.
Даны точки А, В, С, Д.
Плоскость А проходит через точки А, В и Д, но не проходит через точку С.
Назовите три из данных точек, которые могут лежать на одной прямой.
4. Три прямые пересекаются в точке А.
Через какую точку необходимо провести плоскость, содержащую все данные прямые?
Видео:Параллельность прямых. 10 класс.Скачать

Помогите пожалуйста)) 1?
Помогите пожалуйста)) 1.
Если две плоскости имеют общую точку, то … 2.
Две плоскости не параллельны, если … 3.
Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то … 4.
Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти вторые прямые … 5.
Через точку, не принадлежащую данной плоскости, проходит единственная плоскость ….
Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Плоскости Альфа и Бета пересекаются по прямой «а» ; прямая «b», лежащая в плоскости Бета, пересекает Альфа в точке А?
Плоскости Альфа и Бета пересекаются по прямой «а» ; прямая «b», лежащая в плоскости Бета, пересекает Альфа в точке А.
Где лежит точка А?
Видео:№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

Можно ли через точку пересечения двух данных прямых провести третью прямую не лежащую с ними в одной плоскости?
Можно ли через точку пересечения двух данных прямых провести третью прямую не лежащую с ними в одной плоскости?
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Даны прямая и точка, не лежащая на этой прямой?
Даны прямая и точка, не лежащая на этой прямой.
Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Прямая а || в?
Через точку В лежащую на прямой в, проведена плоскость альфа, || прямой а.
Доказать, что плоскость альфа проходит через прямую в.
Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

1. ДАНА ПРЯМАЯ?
СКОЛЬКО ТОЧЕК СОДЕРЖИТ ЭТА ПРЯМАЯ?
2. ПРЯМАЯ ЛЕЖИТ НА ПЛОСКОСТИ.
ЧТО МОЖНО СКАЗАТЬ О ТОЧКАХ ЭТОЙ ПРЯМОЙ?
3. ДАНА ПРЯМАЯ И ТОЧКА.
КАК ОНИ МОГУТ БЫТЬ РАСПОЛОЖЕНЫ?
КАК МОГУТ БЫТЬ РАСПОЛОЖЕНЫ ПРЯМАЯ И ДВЕ ТОЧКИ?
4. СКОЛЬКО ТОЧЕК ОПРЕДЕЛЯЮТ ОДНУ ПРЯМУЮ?
КАК ОНИ ДОЛЖНЫ БЫТЬ РАСПОЛОЖЕНЫ?
5. СКОЛЬКО СУЩЕСТВУЕТ ПЛОСКОСТЕЙ, СОДЕРЖАЩИХ ТРИ ДАННЫЕ ТОЧКИ, ЕСЛИ ЭТИ ТОЧКИ НЕ ПРИНАДЛЕЖАТ ОДНОЙ ПРЯМОЙ.
6. ДАНЫ ПЛОСКОСТЬ a И КВАДРАТ abcd.
МОЖЕТ ЛИ ПЛОСКОСТЬ a принадлежать ; а)только одна вершина ; б)только две вершины квадрата ; в)только три вершины квадрата?
СРОЧНО НУЖНА ПОМОЩЬ И ОТВЕТЫ ЗАВТРА.
Видео:Принадлежность прямой плоскостиСкачать

Даны прямая и точка, не лежащая на этой прямой?
Даны прямая и точка, не лежащая на этой прямой.
Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.
Вы перешли к вопросу В плоскости двух пересекающихся прямых a и b задана точка С, не принадлежащая этим прямым?. Он относится к категории Геометрия, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Можно построить контр пример , так как этот угол из условия однозначный. Зададим сразу расстояние одной из прямых , пусть A1D1 , чтобы не вписывать множество переменных для произвольного шестиугольника , определим координаты 5 вершин произвольным об..
Вот я прикрепил файл. Там все доказано.
Представим треугольник ДВС, тогда один из этих углов будет 60 градусов добавим к этому треугольнику точно такой — же треугольник, то получится, что все углы будут равны, а значит и стороны будут равны. Разделим сторону ДС на пополам, а когда все сто..
Угол 1 = углу 2, угол 6 = углу 3, угол 5 = углу 2 = 112 градусов. Допустим угол6 это Х, тогда угол1 это Х + 10 Тогда угол1 + угол6 + угол5 = 180 градусов. Х + 10 + х + 112 = 180 2х + 122 = 180 2х = 180 — 122 = 58 х = 58 : 2 = 29 — угол 6 и угол 3 т..
Характеристика равнин Равнина — это участок суши или дна моря, имеющий небольшое колебание высот (до 200 м) и незначительный уклон (до 5º). Они встречаются на разных высотах, в том числе и на дне океанов. Отличительная черта равнин — четкая, открыт..
Пусть большая сторона равна Х, тогда вторая сторона (Х — 10). Cos60° = 1 / 2. Сторона против угла 60° равна 14 (дано). По теореме косинусов : 14² = Х² + (Х — 10)² — 2 * Х * (Х — 10) * (1 / 2). Или 196 = Х² + (Х² — 20Х + 100) — Х² + 10Х. Х² — 10Х..
AC — 12 CB — 11 Это очень легко я давно проходила.
У равн. Треугольника боковые стороны равны значиь вторая сторона = 26см что бы найти площадь , нужно узнать высоту, для этого мы чертим высоту, она разделяет равнобедренный треуг. На два прямоугольных, сторона основания прям треуг = 20÷2 = 10см, Вы..
Видео:№94. Даны две скрещивающиеся прямые и точка В, не лежащая на этих прямых. Пересекаются ли плоскостиСкачать

Контрольная работа №2 Вариант 1 Вплоскости двух параллельных прямых a и b дана точка C, не принадлежащая этим прямым. Через нее проведена прямая c. Найдите все возможные расположения прямой
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
§ 3. КОНТРОЛЬНЫЕ РАБОТЫ
Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Контрольная работа № 1
Вариант 1
1. Три вершины ABC параллелограмма ABCD принадлежат одной плоскости a. aБудет ли четвертая вершина D принадлежать этой плоскости? Ответ поясните.
2. Четырехугольник ABCD лежит в плоскости b, а плоскость четырехугольника BCEF не совпадает с плоскостью b. По какой прямой пересекаются плоскости: а) ACD и BCE ; б) CEF и AEF ?
3. Дана прямая и не принадлежащая ей точка. Докажите, что все прямые, проходящие через эту точку и пересекающие данную прямую, лежат в одной плоскости.
4. Найдите наибольшее число плоскостей, которые можно провести через различные тройки из четырех точек.
5*. Найдите наибольшее число прямых, которые можно провести через различные пары из пяти точек.
Вариант 2
1. Две вершины A и B квадрата ABCD и точка O – точка пересечения его диагоналей, принадлежат плоскости b. Совпадает ли плоскость квадрата с плоскостью b. Ответ поясните.
2. Плоскости четырехугольников ABCD и BCEF не совпадают. Найдите прямую по которой пересекаются плоскости: а) BDC и BEC ; б) AFD и ABF .
3. Даны две пересекающиеся прямые. Докажите, что все прямые, пересекающие эти прямые и не проходящие через точку их пересечения, лежат в одной плоскости.
4. Найдите наибольшее число прямых, которые можно провести через различные пары из четырех точек.
5*. Найдите наибольшее число плоскостей, которые можно провести через различные тройки из пяти точек.
Видео:№91. Через каждую из двух параллельных прямых a и b и точку М, не лежащую в плоскости этих прямыхСкачать

Контрольная работа № 2
Вариант 1
1. В плоскости двух параллельных прямых a и b дана точка C , не принадлежащая этим прямым. Через нее проведена прямая c . Найдите все возможные расположения прямой c относительно прямых a и b .
2. Сторона KM треугольника KLM параллельна плоскости a. Точки G и H принадлежат соответственно его сторонам KL и KM . Точка P – точка пересечения прямой GH с плоскостью a. Постройте точки пересечения прямых KL и LM с плоскостью a. Найдите линию пересечения плоскостей треугольника KLM и a.
3. Прямая b параллельна плоскости b. Определите положение данной прямой относительно прямых: а) лежащих в плоскости b; б) параллельных b; в) пересекающих b.
4. Из точки S , не принадлежащей ни одной из двух параллельных плоскостей, проведены три прямые, пересекающие эти плоскости соответственно в точках A 1 , A 2 ; B 1 , B 2 ; C 1 , C 2 . Найдите SA 2 , SB 2 и A 1 C 1 , если SA 1 = A 1 B 1 = 5 см; A 2 C 2 = B 1 B 2 = 12 см; A 2 B 2 = 15 см.
5*. Найдите наибольшее число плоскостей, которые можно провести через различные пары из: а) пяти лучей; б) шести лучей, выходящих из одной точки.
Вариант 2
1. В плоскости двух пересекающихся прямых m и n дана точка A , не принадлежащая этим прямым. Прямая a проходит через точку A . Найдите все возможные расположения прямой a по отношению к прямым m и n .
2. Сторона CD четырехугольника CDEF параллельна плоскости a. Прямая CE пересекает плоскость a в точке G . Постройте точки пересечения прямых CF и DE с плоскостью a. Найдите линию пересечения плоскостей четырехугольника CDEF и a.
3. Даны две скрещивающиеся прямые a и b . Определите положение прямой a относительно третьей прямой c , если: а) c параллельна b ; б) c пересекает b ; в) c скрещивается с b .
4. Из точки O , не принадлежащей ни одной из двух параллельных плоскостей, проведены три прямые, пересекающие плоскости соответственно в точках A , B , C и A 1 , B 1 , C 1 . Найдите BC , если OA = a , AA 1 = b , B 1 C 1 = c .
5*. Найдите наибольшее число прямых, по которым могут попарно пересекаться: а) 5 плоскостей; б) 6 плоскостей.
Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Контрольная работа № 3
Вариант 1
1. В параллелепипеде A … D 1 найдите вектор, равный: а) 


2. Изобразите параллельную проекцию куба A … D 1 , если: а) две грани куба параллельны плоскости проектирования; б) диагональ куба параллельна направлению проектирования.
3. Постройте сечение куба плоскостью, проходящей через одно из его ребер и центр одной из противолежащих граней. Найдите периметр сечения, если ребро куба равно a .
4*. Треугольник A ’ B ’ C ’ является параллельной проекцией равнобедренного треугольника ABC , боковая сторона которого в два раза больше основания. Постройте изображение в этой проекции высоты треугольника ABC , проведенной из вершины основания.
Вариант 2
1. В параллелепипеде A … D 1 найдите вектор, равный: а) 


2. Изобразите параллельную проекцию куба A … D 1 , если: а) какое-нибудь ребро куба параллельно направлению проектирования; б) грани куба не параллельны плоскости проектирования.
3. В правильной 4-угольной призме A … D 1 проведите сечение через середины ребер AB , AD и вершину C 1 . Найдите периметр сечения, если все ребра призмы равны 1.
4*. Треугольник A ’ B ’ C ’ является параллельной проекцией равнобедренного треугольника ABC , боковая сторона которого в два раза больше основания. Постройте изображение в этой проекции биссектрисы треугольника ABC , проведенной из вершины основания.
Видео:10 класс, 3 урок, Некоторые следствия из аксиомСкачать

Контрольная работа № 4
Вариант 1
1. В кубе A … D 1 вершина D соединена с серединой K диагонали A 1 B грани ABB 1 A 1 . Найдите угол между прямыми DK и A 1 B .
2. Из вершины B квадрата ABCD к его плоскости проведен перпендикуляр BM . Определите (относительно углов) виды треугольников ABM , BCM , ADM и CDM .
3. Из вершины K треугольника KLM проведен к его плоскости перпендикуляр KN . Из точки N опущен перпендикуляр на сторону ML . Найдите условие, при котором этот перпендикуляр пересечет продолжение стороны ML .
4. Из точки E , не принадлежащей плоскости a, проведены к ней две наклонные EF и EG , образующие равные углы с прямой FG , лежащей в плоскости a. Докажите, что ортогональные проекции этих наклонных на плоскость a равны.
5*. Докажите, что ортогональная проекция на данную плоскость b угла AOB , образованного двумя равными наклонными OA и OB к этой плоскости, больше угла между самими наклонными.
Вариант 2
1. В кубе A … D 1 вершина C 1 соединена с центром O грани ABCD . Найдите угол между прямыми C 1 O и BD .
2. Из вершины C правильного шестиугольника ABCDEF к его плоскости проведен перпендикуляр CK . Определите (относительно углов) виды треугольников BCK , CDK , DEK , EFK .
3. Из вершины G треугольника GHP проведен перпендикуляр GQ . Из точки Q опущен перпендикуляр на сторону HP . Найдите условие, при котором этот перпендикуляр пройдет через одну из вершин H или P треугольника.
4. Из вершины угла к его плоскости проведена наклонная, которая составляет со сторонами угла равные углы. Докажите, что ортогональной проекцией этой наклонной является биссектриса данного угла.
5*. Докажите, что ортогональная проекция угла на плоскость, проходящую через одну из его сторон, меньше, равна или больше данного угла, смотря по тому, является ли данный угол соответственно острым, прямым или тупым.
Видео:№11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие черезСкачать

Контрольная работа № 5
Вариант 1
1. В равнобедренном прямоугольном треугольнике один из катетов лежит в плоскости a, а другой образует с ней угол 45 0 . Найдите угол между гипотенузой данного треугольника и данной плоскостью.
2. Точка K , не принадлежащая плоскости равностороннего треугольника, удалена от каждой его вершины на расстояние 
3. Угол между плоскостями двух равнобедренных треугольников ABC и BCD , имеющих общую боковую сторону BC , равен 90 0 . Найдите расстояние между точками A и D , если основание каждого треугольника равно a , а каждая боковая сторона равна b .
4. Внутри двугранного угла из точки M , принадлежащей его ребру, проведен к нему перпендикуляр, на котором отложен отрезок MN , в два раза больший своей ортогональной проекции на одну из граней двугранного угла. Найдите угол, который образует MN с другой гранью, если двугранный угол равен 100 0 .
5*. Через данную точку проведите прямую, параллельную данной плоскости и перпендикулярную данной прямой.
Вариант 2
1. Наклонная AB образует с плоскостью a угол 45 0 , прямая AC , лежащая в этой плоскости, составляет угол 45 0 с ортогональной проекцией наклонной AB на плоскость a. Найдите угол BAC .
2. Дан ромб со стороной a и углом 45 0 . Точка L удалена от всех прямых, на которых лежат стороны ромба, на расстояние b . Найдите расстояние от точки L до плоскости ромба.
3. Угол между плоскостями двух равнобедренных треугольников ABC и BCD , имеющих общую боковую сторону BC , равен 120 0 . Расстояние между точками A и D равно m . Основание каждого треугольника равно a . Найдите боковые стороны треугольников.
4. Из точки K , расположенной внутри двугранного угла, проведен перпендикуляр KL на его ребро. Расстояние от точки K до одной из его граней равно ортогональной проекции KL на эту грань. Этот же отрезок KL в два раза больше своей ортогональной проекции на другую грань. Найдите двугранный угол.
5*. Через данную точку проведите плоскость, перпендикулярную двум данным плоскостям.
Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Контрольная работа № 6
Вариант 1
1. Можно ли составить трехгранный угол с плоскими углами: а) 40 0 , 70 0 , 100 0 ; б) 150 0 , 120 0 , 90 0 ?
2. Два плоских угла трехгранного угла равны по 60 0 , а третий равен 90 0 . Найдите угол между плоскостью прямого угла и противоположным ребром трехгранного угла.
3. Основанием наклонного параллелепипеда является ромб, а одно боковое ребро образует с прилежащими сторонами основания параллелепипеда равные углы. Докажите, что вершина параллелепипеда, принадлежащая этому ребру, ортогонально проектируется в точку диагонали основания.
4. Найдите расстояние между центрами двух соседних граней правильного октаэдра, если его ребро равно 1.
5*. Докажите, что любое сечение трехгранного угла с плоскими углами по 90 0 , пересекающее все его ребра, является остроугольным треугольником.
Вариант 2
1. Можно ли составить трехгранный угол с плоскими углами: а) 80 0 , 100 0 , 130 0 ; б) 60 0 , 120 0 , 180 0 ?
2. Плоские углы трехгранного угла равны 45 0 , 45 0 и 60 0 . Найдите двугранный угол, образованный плоскостями равных плоских углов.
3. Основанием пирамиды является прямоугольник, а одно из ее боковых ребер перпендикулярно плоскости основания. Докажите, что все боковые грани пирамиды – прямоугольные треугольники.
4. Найдите расстояние между противоположными параллельными гранями октаэдра, если его ребро равно 1.
5*. Докажите, что двугранный угол между смежными боковыми гранями любой правильной 4-угольной пирамиды является тупым.
Видео:№86. Даны две пересекающиеся прямые а и b и точка А, не лежащая на этих прямых.Скачать

Контрольная работа № 1
Вариант 1
1. Шар диаметра 20 см пересечен плоскостью, отстоящей от его центра на 6 см. Найдите площадь полученного сечения.
2. Через конец радиуса шара проведена плоскость под углом 30 0 к нему. Найдите радиус полученного сечения, если радиус шара равен 1.
3. Найдите радиус сферы, описанной около правильной треугольной призмы, все ребра которой равны a .
4. В прямую призму, основанием которой является ромб с диагоналями 6 см и 8 см, вписана сфера. Определите боковое ребро призмы и радиус вписанной в нее сферы.
5*. В сферу вписана четырехугольная пирамида, у которой все ребра равны. Докажите, что центр основания пирамиды является центром сферы.
Вариант 2
1. Шар пересечен плоскостью, отстоящей от его центра на 8 см. Площадь полученного сечения равна 125p см 2 . Найдите радиус шара.
2. Диаметр шара равен D . Через его конец под углом 45 0 к нему проведена плоскость. Найдите площадь полученного сечения.
3. Около прямоугольного параллелепипеда, ребра которого равны 1 дм, 2 дм и 2 дм, описана сфера. Найдите ее радиус.
4. В правильную треугольную призму, площадь основания призмы равна 27 
5*. Боковые ребра правильной пирамиды наклонены к плоскости основания под углом 45 0 . Где расположен центр описанной сферы относительно пирамиды?
Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Контрольная работа № 2
Вариант 1
1. Нарисуйте фигуру, которая получается вращением равнобедренного треугольника вокруг его боковой стороны. Как можно получить эту фигуру из конусов?
2. В сферу вписан конус, высота которого равна 3 см, радиус основания равен 3 
3. Найдите радиус основания и образующую цилиндра, описанного около сферы радиуса R .
4. Сколько: а) осей симметрии; б) плоскостей симметрии имеет прямоугольный параллелепипед, у которого нет квадратных граней? Назовите их.
5*. Внутри двугранного угла, равного 30 0 , взята точка, удаленная от его граней на 2 см и 3 
1. Нарисуйте фигуру, которая получается при вращении равнобедренного треугольника вокруг прямой, перпендикулярной его боковой стороне и проходящей через вершину, лежащую против основания. Как можно получить эту фигуру из конусов?
2. В сферу вписан усеченный конус, радиусы оснований которого равны 15 см и 24 см, высота равна 27 см. Найдите радиус сферы.
3. Образующая конуса равна 20 см, радиус основания равен 16 см. Найдите радиус вписанной в конус сферы.
4. В основании прямой призмы лежит ромб. Сколько она имеет: а) осей симметрии; б) плоскостей симметрии? Назовите их.
5*. Прямая, проведенная через вершину прямого угла, образует с его сторонами углы 60 0 и 45 0 . Найдите угол между этой прямой и плоскостью прямого угла.
Видео:Параллельные прямые. 6 класс.Скачать

Контрольная работа № 3
Вариант 1
1. Осевое сечение цилиндра – квадрат, диагональ которого равна 6 см. Найдите объем цилиндра.
2. Основанием прямого параллелепипеда является ромб, площадь которого равна 8 дм 2 . Площади диагональных сечений равны 24 дм 2 и 48 дм 2 . Найдите объем параллелепипеда.
3. Основанием пирамиды является прямоугольный треугольник с катетами a и a 
4. Высота конуса равна 12 см, периметр осевого сечения 36 см. Найдите объем конуса.
5*. Найдите объем тела, которое образуется при вращении правильного шестиугольника со стороной a вокруг апофемы (высота, опущенная из центра правильного многоугольника на его сторону).
Вариант 2
1. В цилиндре через середину радиуса основания перпендикулярно ему проведено сечение. В сечении получился квадрат площадью 16 см 2 . Найдите объем цилиндра.
2. Основанием прямой четырехугольной призмы является ромб, диагонали которого относятся как 5:2. Диагонали призмы равны 17 дм и 10 дм. Найдите объем призмы.
3. Основанием пирамиды является равнобедренный треугольник, основание которого равно 12 см, а боковая сторона – 10 см. Найдите объем пирамиды, если каждая ее боковая грань наклонена к плоскости основания под углом 45 0 .
4. Площадь осевого сечения равностороннего конуса равна Q 
5*. Найдите объем тела, которое образуется при вращении правильного шестиугольника со стороной a вокруг его малой диагонали.
Контрольная работа № 4
Вариант 1
1. Найдите отношение площадей поверхностей двух шаров, если диаметр одного из них в два раза больше диаметра другого.
2. Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом b. Найдите площадь поверхности пирамиды, если сторона ромба равна a , а его острый угол равен a.
3. Площадь боковой поверхности цилиндра равна половине площади его полной поверхности. Найдите площадь поверхности цилиндра, если диагональ его осевого сечения равна 5 см.
4. Через вершину конуса проведено сечение, пересекающее основание по хорде, равной 4 дм и отсекающей дугу 90 0 . Найдите площадь боковой поверхности конуса, если угол при вершине осевого сечения равен 60 0 .
5*. Образующая усеченного конуса равна 4 см и наклонена к плоскости основания под углом 60 0 . Найдите площадь боковой поверхности усеченного конуса, если радиус его большего основания равен 5 см.
Вариант 2
1. Объем одного шара равен 2 см 3 , другого – 3 см 3 . Найдите отношение площадей их поверхностей.
2. В основании пирамиды лежит квадрат, две ее боковые грани перпендикулярны основанию, а две другие составляют с ним равные углы j. Найдите площадь боковой поверхности пирамиды, если ее высота равна h .
3. Разверткой боковой поверхности цилиндра является прямоугольник, одна сторона которого в два раза больше другой. Площадь боковой поверхности цилиндра равна 20 дм 2 . Найдите площадь его поверхности.
4. Через две образующие конуса проведена плоскость, отсекающая от основания дугу в 120 0 и образующая с плоскостью основания угол 45 0 . Найдите площадь боковой поверхности конуса, если радиус его основания равен 4 см.
5*. Радиусы оснований усеченного конуса равны 2 см и 7 см, диагональ осевого сечения равна 15 см. Найдите площадь боковой поверхности усеченного конуса.
Контрольная работа № 5
Вариант 1
1. Найдите расстояние от точки A (1,-2,3) до: а) координатной плоскости Oyz ; б) начала координат; в) координатной прямой Ox .
2. Даны точки B (3,0,-2) и C (-2,6,-4). Найдите координаты вектора: а) 


3. Даны векторы 





4. Напишите уравнение плоскости, которая проходит через точку M (5,-4,1) и параллельна плоскости 2 x – y – z + 3 = 0.
5*. Точка движется прямолинейно и равномерно в направлении вектора 
Вариант 2
1. Найдите расстояние от точки B (-2,3,4) до: а) начала координат; б) координатной плоскости Oxz ; в) координатной прямой Oy .
2. Даны точки C (5,0,-2) и D (-1,2,-3). Найдите координаты вектора: а) 


3. Найдите угол, под которым виден отрезок EF из начала координат, если E (5, 
4. Напишите уравнение плоскости, перпендикулярной прямой KL и проходящей через точку L (-3,2,-1), если K (7,-11,3).
5*. Точка движется прямолинейно и равномерно. В момент времени t = 1 она имела координаты (2,-3,4), а в момент времени t = 3 координаты (-1,4,-2). С какой скоростью движется точка?
Контрольная работа № 1
1. Дана прямая a и точка A . Сколько плоскостей можно провести через данную прямую и данную точку? Ответ объясните.
2. Докажите, что если плоскость и прямая, не лежащая на ней, имеют общую точку, то эта точка единственная.
3. Даны две пересекающиеся прямые a и b . Как может располагаться прямая a относительно третьей прямой c , если: а) c параллельна b ; б) c пересекается с b ; в) c скрещивается c b .
4. Найдите число диагоналей: а) пятиугольника; б) пятиугольной призмы.
5*. Ребро куба A … D 1 равно 1. Определите расстояние от центра грани ABCD до точки пересечения прямой C 1 M , где M – середина ребра AA 1 , и плоскости грани ABCD .
1. Даны три точки A , B , C . Сколько плоскостей можно провести через данные точки? Ответ объясните.
2. Докажите, что если в двух пересекающихся плоскостях лежат две пересекающиеся прямые (по одной в каждой плоскости), то точка пересечения прямых принадлежит прямой пересечения этих плоскостей.
3. Даны две параллельные прямые a и b . Как может располагаться прямая b относительно третьей прямой c , если: а) c параллельна a ; б) c пересекается с a ; в) c скрещивается c a .
4. Найдите число диагоналей: а) шестиугольника; б) шестиугольной призмы.
5*. Ребро куба A … D 1 равно a . Найдите длину отрезка OK , где O – центр грани ABCD , K – точка пересечения прямой A 1 L , где L – середина ребра C 1 C , и плоскости грани ABCD .
Контрольная работа № 2
1. Дан куб A … D 1 . Плоскостям каких граней куба параллельна плоскость, в которой лежит его грань CDD 1 C 1 ?
2. Даны две параллельные прямые, не лежащие в данной плоскости. Докажите, что если одна из них параллельна данной плоскости, то и другая прямая параллельна этой плоскости.
3. Параллелограмм ABCD является изображением в параллельной проекции ромба, тупой угол которого равен 120 0 . Постройте на изображении ромба изображение его высот, проведенных из данного угла.
4. Постройте сечение правильной четырехугольной пирамиды плоскостью, проходящей через диагональ основания пирамиды параллельно ее боковому ребру.
5*. Два треугольника ABC и ADE имеют общую вершину A , а их стороны BC и DE лежат в одной плоскости. Постройте прямую пересечения плоскостей ABC и ADE , если BC и DE не параллельны.
1. Дан куб A … D 1 . Плоскостям каких граней куба параллельна прямая, содержащая ребро BB 1 ? Почему?
2. Докажите, что если прямая параллельна одной из двух параллельных плоскостей, то она параллельна и другой плоскости.
3. На изображении в параллельной проекции прямоугольного треугольника с острым углом 30 0 постройте изображение биссектрисы этого угла.
4. Постройте сечение правильной треугольной пирамиды плоскостью, проходящей через центр основания пирамиды параллельно ее боковой грани.
5*. Два треугольника ABC и ADE имеют общую вершину A , а их стороны BC и DE лежат в одной плоскости. Постройте прямую пересечения плоскостей ABC и ADE , если BC и DE параллельны.
1. Из точки O – точки пересечения диагоналей прямоугольника ABCD , к его плоскости проведен перпендикуляр. Докажите, что любая точка этого перпендикуляра равноудалена от вершин A , B , C , D .
2. Вершина B 1 куба A … D 1 соединена с точкой O – центром грани ABCD . Найдите угол между прямыми AC и B 1 O .
3. Из точки вне плоскости проведены к ней две наклонные, по 6 см каждая. Найдите расстояние между их концами, если каждая наклонная образует с плоскостью угол в 30 0 и угол между их проекциями на эту плоскость равен 120 0 .
4. Плоскости правильного треугольника ABC и треугольника ACD образуют между собой угол в 30 0 , причем вершина D проектируется в центр правильного треугольника, высота которого равна 3 см. Определите длину BD .
5*. Из точки M , лежащей внутри двугранного угла, опущен перпендикуляр MH на его ребро. Расстояние от точки M до одной из граней данного двугранного угла равно проекции MH на эту грань. Отрезок MH в два раза больше, чем его проекция на вторую грань. Найдите двугранный угол.
1. Точка O – точка пересечения диагоналей параллелограмма ABCD . Точка M не принадлежит плоскости параллелограмма. Докажите, что MO – перпендикуляр к плоскости параллелограмма, если MA = MC и MB = MD .
2. Дан куб A … D 1 . Найдите угол между прямыми AE и D 1 C , где E – середина DC 1 .
3. Из точки вне плоскости проведены к ней две наклонные, каждая из которых образует с плоскостью угол в 45 0 . Найдите расстояние от данной точки до данной плоскости, если угол между наклонными равен 60 0 и расстояние между концами наклонных равно 10 см.
4. Найдите расстояние от вершины прямого угла C треугольника ABC до плоскости, проходящей через сторону AB под углом 30 0 к плоскости треугольника, если AC =20 см и BC =15 см.
5*. В одной грани двугранного угла проведена прямая под углом 30 0 к другой грани и под углом 45 0 к ребру. Найдите двугранный угол.
Контрольная работа № 4
1. В прямом круговом конусе с радиусом основания 5 см и высотой 12 см на расстоянии 3 см от вершины проведено сечение, параллельное основанию. Найдите диаметр круга, получившегося в сечении.
2. В выпуклом многограннике число вершин равно В, причем в каждой вершине сходится одно и то же число ребер, равное m . Найдите число плоских углов, ребер и граней данного многогранника.
3. Как изменится число вершин, ребер и граней выпуклого многогранника, если к одной из его граней пристроить пирамиду?
4. Найдите ребро октаэдра, вписанного в куб, если ребро куба равно 1.
5*. Докажите, что не существует выпуклого многогранника с семью ребрами.
1. В правильной треугольной пирамиде со стороной основания, равной 6 см, и высотой 18 см на расстоянии 9 см от вершины проведено сечение, параллельное основанию. Найдите сторону треугольника, получившегося в сечении.
2. В выпуклом многограннике известно число граней Г, причем каждая грань имеет одно и то же число сторон n. Найдите число плоских углов, ребер и вершин данного многогранника.
3. Как изменится число вершин, ребер и граней выпуклого многогранника, если от него отсечь один из его углов?
4. Найдите ребро правильного тетраэдра, вписанного в правильный тетраэдр, если ребро описанного тетраэдра равно 1.
5*. Существует ли выпуклый многогранник, у которого 13 граней и в каждой грани по 13 сторон?
Контрольная работа № 5
1. Шар диаметром 20 см пересечен плоскостью, отстоящей от его центра на 6 см. Найдите площадь полученного сечения.
2. Через конец радиуса шара проведена плоскость под углом 30 0 к нему. Найдите радиус полученного сечения, если радиус шара равен 1.
3. Найдите радиус сферы, описанной около правильной треугольной призмы, все ребра которой равны a .
4. В прямую призму, основанием которой является ромб с диагоналями 6 см и 8 см, вписана сфера. Найдите боковое ребро призмы и радиус вписанной в нее сферы.
5*. В сферу вписана четырехугольная пирамида, у которой все ребра равны. Докажите, что центр основания пирамиды является центром сферы.
1. Шар пересечен плоскостью, отстоящей от его центра на 8 см. Площадь полученного сечения равна 125p см 2 . Найдите радиус шара.
2. Диаметр шара равен D . Через его конец под углом 45 0 к нему проведена плоскость. Найдите площадь полученного сечения.
3. Около прямоугольного параллелепипеда, ребра которого равны 1 дм, 2 дм и 2 дм, описана сфера. Найдите ее радиус.
4. В правильную треугольную призму вписана сфера. Площадь основания призмы равна 27 
5*. Боковые ребра правильной пирамиды наклонены к плоскости основания под углом 45 0 . Где расположен центр описанной сферы относительно пирамиды?
Контрольная работа № 6
1. Нарисуйте фигуру, которая получается вращением равнобедренного треугольника вокруг его боковой стороны. Как можно получить эту фигуру из конусов?
2. В сферу вписан конус, высота которого равна 3 см, радиус основания равен 3 
3. Найдите радиус основания и образующую цилиндра, описанного около сферы радиуса R .
4. Сколько: а) осей симметрии; б) плоскостей симметрии имеет прямоугольный параллелепипед, у которого нет квадратных граней? Назовите их.
5*. Внутри двугранного угла, равного 30 0 , взята точка, удаленная от его граней на 2 см и 3 
1. Нарисуйте фигуру, которая получается при вращении равнобедренного треугольника вокруг прямой, перпендикулярной его боковой стороне и проходящей через вершину, лежащую против основания. Как можно получить эту фигуру из конусов?
2. В сферу вписан усеченный конус, радиусы оснований которого равны 15 см и 24 см, высота равна 27 см. Найдите радиус сферы.
3. Образующая конуса равна 20 см, радиус основания равен 16 см. Найдите радиус вписанной в конус сферы.
4. В основании прямой призмы лежит ромб. Сколько она имеет: а) осей симметрии; б) плоскостей симметрии? Назовите их.
5*. Прямая, проведенная через вершину прямого угла, образует с его сторонами углы 60 0 и 45 0 . Найдите угол между этой прямой и плоскостью прямого угла.
1. Докажите, что уравнение: а) 8 x 2 +3 y 2 =48; б) 25 x 2 +4 y 2 =16 задает на плоскости эллипс. Найдите его большую и малую полуосей.
2. Определите, какая фигура получится при вращении: а) правильной пятиугольной пирамиды вокруг ее высоты; б) прямой призмы, в основании которой лежит трапеция, вокруг ее бокового ребра.
3. Найдите объем цилиндра, высота которого равна 5 см, если известно, что при увеличении высоты цилиндра на 4 см, его объем увеличивается на 36p см 3 .
4. В основании прямого параллелепипеда лежит ромб, диагонали которого относятся как 5:2. Диагонали параллелепипеда равны 17 см и 10 см. Найдите объем параллелепипеда.
5*. Около октаэдра описан цилиндр. Две вершины октаэдра лежат в центрах оснований цилиндра, а остальные четыре – на боковой поверхности цилиндра. Найдите объем цилиндра, если ребро октаэдра равно a .
1. Для параболы, заданной уравнением y = 
2. Определите, какая фигура получится при вращении: а) правильной призмы вокруг прямой, соединяющей центры ее оснований; б) пирамиды, в основании которой лежит ромб и вершина проектируется в точку пересечения его диагоналей.
3. В цилиндре через середину радиуса основания перпендикулярно ему проведено сечение. В сечении получился квадрат площадью 16 см 2 . Найдите объем цилиндра.
4. В основании прямого параллелепипеда лежит ромб, диагонали которого равны 1 дм и 7 дм. Диагонали параллелепипеда относятся как 13:37. Найдите объем параллелепипеда.
5*. В прямую призму, основанием которой является равнобедренная трапеция, вписан куб таким образом, что его вершины лежат в серединах сторон оснований призмы. Найдите объем призмы, если ребро куба равно a .
Контрольная работа № 2
1. Найдите объем наклонной призмы, в основании которой лежит правильный шестиугольник со стороной 4 см. Боковое ребро призмы, равное 5 см, наклонено к плоскости основания под углом 60 0 .
2. Основанием пирамиды является прямоугольный треугольник с катетами a и a 
3. Высота конуса равна 12 см, периметр осевого сечения – 36 см. Найдите объем конуса.
4. Найдите объем правильной усеченной пирамиды, если радиусы описанных около ее оснований окружностей равны 2 см и 8 см, а боковые грани наклонены к плоскости основания под углом 30 0 .
5*. Основанием наклонного параллелепипеда является прямоугольник со сторонами 4 см и 6 см, боковое ребро равно 2 см и образует со смежными сторонами основания углы по 60 0 . Найдите объем параллелепипеда.
1. В основании наклонной призмы лежит равнобедренная трапеция с основаниями 5 см и 9 см и острым углом 45 0 . Найдите объем призмы, если ее боковое ребро, равное 7 см, наклонено к плоскости основания под углом 30 0 .
2. Основанием пирамиды является равнобедренный треугольник, у которого основание равно 12 см, а боковая сторона – 10 см. Найдите объем пирамиды, если каждая ее боковая грань наклонена к плоскости основания под углом 45 0 .
3. Площадь осевого сечения равностороннего конуса равна Q 
4. Найдите объем правильной треугольной усеченной пирамиды, если радиусы вписанных в ее основания окружностей равны 1 см и 2 см, а боковые ребра наклонены к плоскости основания под углом 30 0 .
5*. Основанием наклонного параллелепипеда является квадрат со стороной 15 см. Боковое ребро, равное 14 см, образует с прилежащими сторонами основания равные острые углы. Расстояние между соответствующими сторонами двух оснований равно 10 см. Найдите объем параллелепипеда.
Контрольная работа № 3
1. Шар пересечен плоскостью, отстоящей от его центра на расстояние 8 см. Найдите объем шара, если площадь сечения равна 36p см 2 .
2. Плоскость, параллельная оси цилиндра, делит окружность основания в отношении 1:5. Площадь образовавшегося сечения равна 10 см 2 . Найдите площадь боковой поверхности цилиндра.
3. Найдите площадь боковой поверхности конуса, если площадь его основания равна Q , а площадь осевого сечения равна q .
4. Прямоугольный треугольник, катеты которого равны 3 см и 4 см, вращается вокруг гипотенузы. Найдите объем и площадь поверхности тела вращения.
5*. Радиус шара равен 25 см. Найдите площадь поверхности частей шара, на которые он делится сечением площадью 49p см 2 .
1. Сечение шара плоскостью, которая отстоит от его центра на 3 см, имеет радиус, равный 4 см. Найдите объем шара.
2. Плоскость, параллельная оси цилиндра, отстоит от нее на расстоянии 9 см. Образующая цилиндра равна 10 см. Найдите площадь полной поверхности цилиндра, если площадь образовавшегося сечения равна 240 см 2 .
3. Расстояние от центра основания равностороннего конуса до его образующей равно a . Найдите площадь полной поверхности конуса.
4. Прямоугольный треугольник, катеты которого равны 5 см и 12 см, вращается вокруг оси, параллельной меньшему катету, проходящей через вершину прямого угла и лежащей в плоскости треугольника. Найдите объем и площадь поверхности тела вращения.
5*. Радиусы оснований шарового пояса равны 10 см и 12 см, высота пояса равна 11 см. Найдите площадь поверхности данного шарового пояса.
Контрольная работа № 4
1. Найдите координаты точки:
а) симметричной точке A (-1,2,-3) относительно начала координат;
б) относительно которой симметричны точки M (2,-4,7) и N (-1,6,-10);
в) симметричной точке K (3,-8,9) относительно координатной плоскости Oy z.
2. Найдите координаты точки, принадлежащей оси Ox и равноудаленной от точек A (-4,0,6) и B (1,2,-10).
3. Найдите координаты конца вектора 
4. В параллелепипеде A … D 1 , найдите:
а) 

5*. Дан треугольник ABC , M – точка пересечения его медиан, O – произвольная точка пространства. Докажите, что выполняется следующее равенство: 
1. Найдите координаты точки:
а) относительно которой симметричны точки K (8,-5,11) и L (-6,10,0);
б) симметричной точке B (3,-5,-2) относительно точки N (6,0,-3);
в) симметричной точке M (-1,2,-4) относительно координатной плоскости Ox z.
2. Найдите координаты точки, принадлежащей оси O z и равноудаленной от точек C (4,5,0) и D (-2,3,6).
3. Найдите координаты начала вектора 
4. В параллелепипеде A … D 1 , найдите:
а) 

5*. В пространстве даны два треугольника ABC и A 1 B 1 C 1 ; M и M 1 – соответствующие точки пересечения их медиан. Докажите, что 
Контрольная работа № 5
1. Найдите скалярное произведение векторов 

2. При каком значении m векторы (3 m 



3. Запишите уравнение плоскости, если она:
а) перпендикулярна оси Oz и проходит через точку A (0,0,-2);
б) параллельна плоскости Oxz и проходит через точку B (1,-3,2).
4. Найдите угол между плоскостями 2 x +3 y +6 z +5=0 и
5*. Точка движется прямолинейно и равномерно в направлении вектора 
1. Найдите их скалярное произведение и угол между векторами 

2. При каком значении t векторы 5 



3.Запишите уравнение плоскости, если она:
а) перпендикулярна оси Oy и проходит через точку C (0,4,0);
б) параллельна плоскости Oy z и проходит через точку D (2,1,-3).
4. Найдите угол между плоскостями 2 x — y +2 z -7=0 и 4 x -3 y +5=0.
5*. Точка движется прямолинейно и равномерно. В момент времени t =1 она имела координаты (2,-3,4), а в момент времени t =3 – координаты (-1,4,-2). С какой скоростью движется точка?
Контрольная работа № 6
1. Изобразите в полярной системе координат точки: а) A (2, 



2. Постройте кривую, заданную уравнением r = 
3. Найдите декартовы координаты точек пространства, заданных своими сферическими координатами: а) (1,-45 0 ,270 0 ); б) (3,120 0 ,-90 0 ).
4. Найдите сферические координаты точек пространства, заданных своими декартовыми координатами:
а) (0, 


5*.Изобразите в полярной системе координат кривую r = cos 2j.
1. Изобразите в полярной системе координат точки: а) K (1, 


2. Постройте кривую, заданную уравнением r = 2sin 2j.
3. Найдите сферические координаты точек пространства, заданных своими декартовыми координатами:
а) (- 




4. Найдите декартовы координаты точек пространства, заданных своими сферическими координатами: а) (2,135 0 ,-180 0 ); б) (1,-60 0 ,150 0 ).
5*.Изобразите в полярной системе координат кривую r = cos 3j.
ГУМАНИТАРНЫЕ КЛАССЫ
Контрольная работа № 1
Вариант 1
1. Прямые a и b пересекаются. Докажите, что прямая c , пересекающая их в двух различных точках, лежит с ними в одной плоскости.
2. Можно ли провести через точку пересечения диагоналей прямоугольника прямую, которая не пересекает его сторон?
3. Сторона AC треугольника ABC лежит в плоскости α. Вершина B не принадлежит этой плоскости. Докажите, что прямая, проходящая через середины сторон AB и BC , параллельна плоскости α.
4. Через точку K , не лежащую между параллельными плоскостями a и β, проведены прямые a и b . Прямая a пересекает плоскости a и β в точках A 1 и A 2 соответственно, прямая b — в точках B 1 и B 2 . Найдите отрезок B 1 B 2 , если A 2 B 2 : A 1 B 1 =9:4, KB 1 =8см.
5*. Докажите, что если плоскость пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость.
Вариант 2
1. Даны четыре точки, три из которых принадлежат одной прямой. Докажите, что все данные точки принадлежат одной плоскости.
2. Можно ли через вершину треугольника провести прямую, которая не лежит в его плоскости?
3. Через основание AD трапеции ABCD проведена плоскость a. Основание BC не лежит в плоскости a. Докажите, что прямая, проходящая через середины сторон AB и CD , параллельна плоскости a.
4. Через точку M , лежащую между параллельными плоскостями a и b, проведены прямые a и b . Прямая a пересекает плоскости a и b в точках A 1 и A 2 соответственно, прямая b — в точках B 1 и B 2 . Найдите отрезок MB 2 , если A 1 B 1 : A 2 B 2 =3:4, B 1 B 2 =14 см.
5*. Докажите, что если прямая пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость.
Контрольная работа № 2
Вариант 1
1. На изображении квадрата ABCD постройте: а) изображение центра описанной около квадрата окружности; б) изображение прямой, проведенной через вершину B параллельно диагонали AC .
2. Верно ли утверждение, что прямая, лежащая в одной из двух параллельных плоскостей, параллельна другой плоскости?
3. Сторона равностороннего треугольника ABC равна 12 см. Точка K находится на равном расстоянии от его вершин и удалена от плоскости треугольника на 4 см. Найдите: а) длину проекции отрезка KA на плоскость треугольника; б) расстояние от точки K до вершины треугольника.
4. Из точек A и B , принадлежащих двум перпендикулярным плоскостям, проведены в них перпендикуляры AC и BD к линии пересечения плоскостей. Найдите отрезок AB , если AC =12 см, BD =15 см, CD =16 см.
5*. Докажите, что плоскость, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.
Вариант 2
1. На изображении равностороннего треугольника ABC постройте: а) изображение высоты данного треугольника, проведенной к стороне BC ; б) изображение биссектрисы угла C данного треугольника.
2. Прямые a и b расположены соответственно в плоскостях α и β. Верно ли утверждение, что эти прямые не имеют общих точек?
3. Сторона квадрата ABCD равна 8см. Точка M удалена от каждой его вершины на 16 см. Найдите: а) проекцию отрезка MA на плоскость квадрата; б) расстояние от точки M до плоскости квадрата.
4. Из точек M и K , принадлежащих двум перпендикулярным плоскостям, проведены в них перпендикуляры MC и KD к линии пересечения плоскостей. Найдите отрезок С D , если MC =8 см, KD =9 см, MK =17 см.
5*. Докажите, что плоскость, пересекающая одну из параллельных плоскостей под углом j, пересекает и другую под тем же углом j.
Вариант 1
1. Вычислите площадь поверхности икосаэдра, ребро которого равно a .
2. Высота правильной четырехугольной пирамиды равна 8 см, сторона ее основания — 12 см. Найдите: а) боковое ребра; б) площадь боковой поверхности пирамиды.
3. Боковое ребро MA пирамиды MABC перпендикулярно плоскости ее основания; AB = AC = a ; 
4*. Сторона основания правильной шестиугольной призмы равна a , наибольшая диагональ призмы наклонена к плоскости основания под углом a. Найдите высоту призмы.
Вариант 2
1. Вычислите площадь поверхности октаэдра, ребро которого равно a .
2. Высота правильной треугольной пирамиды равна 4 
3. Основанием пирамиды MABCD является квадрат, сторона которого равна a . Боковое ребро MD перпендикулярно плоскости основания. Угол между плоскостью грани MAB и плоскостью основания равен α. Найдите расстояние от вершины пирамиды до прямой AC .
4*. Сторона основания правильной шестиугольной призмы равна a , наименьшая диагональ призмы наклонена к плоскости основания под углом a. Найдите высоту призмы.
Контрольная работа № 4
Вариант 1
1. Образующая конуса равна 18 см. Угол между образующей и плоскостью основания 60 0 . Найдите высоту и площадь основания конуса.
2. Высота цилиндра равна h , радиус его основания R . Через хорду основания проведена плоскость, параллельная оси цилиндра. Угол между радиусами, проведенными в концы хорды, равен 2a. Найдите площадь сечения.
3. Назовите элементы симметрии правильной четырехугольной пирамиды.
4*. Какими свойствами должен обладать усеченный конус, чтобы в него можно было вписать шар?
Вариант 2
1. Диагональ осевого сечения цилиндра равна 32 см и наклонена к плоскости его основания под углом 30 0 . Найдите высоту и площадь основания цилиндра.
2. Через вершину конуса, высота которого равна h , проведено сечение. Угол между плоскостями сечения и основания равен a. Угол при вершине сечения равен 2b. Найдите радиус основания конуса.
3. Назовите элементы симметрии правильной шестиугольной пирамиды.
4*. Какими свойствами должна обладать пирамида, чтобы в нее можно было вписать сферу?
Контрольная работа № 5
Вариант 1
1. Основанием прямого параллелепипеда является ромб, диагонали которого равны 24 см и 10 см. Угол между меньшей диагональю параллелепипеда и плоскостью основания равен 45 0 . Найдите: а) объем параллелепипеда; б) его большую диагональ.
2. Длина окружности сечения шара плоскостью, удаленной от его центра на 3 см, равна 6π см. Найдите объем и площадь поверхности шара.
3. Угол между плоскостью сечения прямого кругового конуса, проходящей через его вершину, и плоскостью его основания равен j. Хорда, являющаяся основанием сечения, равна 2 a и удалена от центра основания конуса на расстояние, равное a . Найдите: а) объем конуса; б) площадь его боковой поверхности.
4*. Равнобедренный треугольник с углом при вершине 2j вращается вокруг прямой, параллельной его основанию и проходящей через его вершину. Высота треугольника, проведенная к его основанию, равна h . Найдите: а) объем фигуры вращения; б) площадь ее поверхности.
Вариант 2
1. Основание прямой призмы A . C 1 — равнобедренный треугольник, в котором AB = AC =17 см, BC =8 см. Угол между плоскостью, содержащей прямую BC и вершину A 1 , и плоскостью основания равен 30 0 . Найдите: а) объем призмы; б) площадь сечения призмы указанной плоскостью.
2. Площадь сечения шара плоскостью равна 36p см 2 . Радиус шара, проведенный в точку окружности сечения, составляет с его плоскостью угол 45 0 . Найдите объем и площадь поверхности шара.
3. Диагональ сечения прямого кругового цилиндра плоскостью, параллельной его оси, равна 2 a и наклонена к плоскости основания под углом 
4*. Прямоугольный треугольник с катетами 3 см и 4 см вращается вокруг своей гипотенузы. Найдите: а) объем фигуры вращения; б) площадь ее поверхности.
Контрольная работа № 6
Вариант 1
1. Запишите разложение по координатным векторам векторов: а) 



2. Найдите угол φ между векторами 

3. Найдите точку, расположенную в плоскостях Oyz и 7 x +3 y -5 z -3=0 и имеющую координату z =3.
4. Составьте уравнение плоскости, проходящей через ось Ox и точку M (2,1,5).
5*. Под действием силы 

Вариант 2
1. Даны векторы 






2. Найдите угол φ между векторами 

3. Найдите точку, расположенную в плоскостях 2 x +5 y +6 z +4=0 и плоскости Oxy , имеющую ординату, равную 2.
4. Составьте уравнение плоскости, проходящей через ось Oz и точку N (4,-2,3).
5*. Три силы 


В1. 1. Да. 2. а) BC ; б) EF . 4. 4. 5*. 10. В2. 1. Да. 2. а) BC ; б) AF . 4. 6. 5*. 10.
В1. 1. Прямая c может быть параллельна прямым a и b ; может пересекать каждую из прямых a и b ; может скрещиваться с каждой из них. 3. а) Параллельны или скрещиваются с b ; б) пересекаются, параллельны или скрещиваются с b ; в) пересекаются или скрещиваются с b . 4. SA 2 = 15 см; SB 2 = 18 см; A 1 C 1 = 4 см. 5*. а) 10; б) 15. В2. 1. Прямая a может пересекать прямые m и n в точке их пересечения или в различных точках данных прямых; может пересекать одну из них и быть параллельной другой; может скрещиваться с каждой из них. 3. а) c пересекается или скрещивается с a ; б), в) пересекается, параллельна или скрещивается с a . 4. BC = 
В1. 1. а) 







В1. 1. 90 0 . 2. Прямоугольные. 3. Угол KLM – тупой. В2. 1. 90 0 . 2. Треугольник DEK тупоугольный, остальные прямоугольные. 3. Угол H или угол P – прямой.
В1. 1. 30 0 . 2. 1 см. 3. 


В1. 1. а) Да; б) нет. 2. 45 0 . 4. 

В1. 1. 64 



В1. 2. 6 см. 3. R , 2 R . 4. а) 3; б) 3. 5*. 14 см. В2. 2. 25 см. 3. 
В1. 1. 







В1. 1. 1:4. 2. 










В1. 1. а) 1; б) 









В1. 4. а) 5; б) 10. 5*. 

В1. 2. 90 





В1. 1. 2,5 см. 2. 







В1. 1. 64 



В1. 2. 6 см. 3. R , 2 R . 4. а) Три оси, проходящие через центры противоположных граней; б) три плоскости, проходящие через середины параллельных ребер. 5*. 14 см. В2. 2. 25 см. 3. 5 

В1. 1. а) 





В1. 1. 180 см 3 . 2. 




В1. 1. 1333 












В1. 1. а) (1,-2,3); б) ( 









В1. 1. 1, cos 










В1. 3. а) ( 















В1. 2. Да. 4. 10 см. В2. 2. Да. 4. 8 см.
В1. 2. Да. 3. а) 4 


В1. 1. 5 






В1. 1. 




В1. 1. а) 1200 см 3 ; б) 26 см. 2. 72 




























В1. 1. а) 






Самостоятельные работы (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
§ 2. САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
1. Основные понятия и аксиомы стереометрии
1. Изобразите прямую a и точки A, B и C, не принадлежащие данной прямой. Сделайте необходимые записи.
2. Изобразите плоскость b, точки E, F, принадлежащие ей, и точку G, ей не принадлежащую. Сделайте необходимые записи.
3. Изобразите прямую a, лежащую в плоскости a. Сделайте необходимую запись.
4. Изобразите две пересекающиеся плоскости a и b. Сделайте необходимую запись.
1. Изобразите две пересекающиеся в точке O прямые a и b и точки A, B, C, причем точка A принадлежит прямой a, B принадлежит прямой b, точка C не принадлежит данным прямым.
2. Изобразите плоскость g, не принадлежащие ей точки K, L и принадлежащую ей точку M. Сделайте необходимые записи.
3. Изобразите прямую b, пересекающую плоскость b в точке O. Сделайте необходимую запись.
4. Изобразите три пересекающиеся по прямой a плоскости a, b и g. Сделайте необходимую запись.
1. Из следующих предложений укажите аксиомы, определения, теоремы:
1) Углы при основании равнобедренного треугольника равны.
2) Через две точки пространства проходит единственная прямая.
3) Вертикальные углы равны.
4) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
2. Определите взаимное расположение плоскостей a и b, если в них лежит треугольник ABC. Ответ обоснуйте.
3. Сколько плоскостей может проходить через три точки?
4. Найдите наибольшее число прямых, проходящих через различные пары из четырех точек.
1. Из следующих предложений укажите аксиомы, определения, теоремы:
1) Если две плоскости имеют общую точку, то они пересекаются по прямой.
2) Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
3) Для прямых и плоскостей в пространстве выполняются аксиомы планиметрии.
4) Диагонали параллелограмма точкой пересечения делятся пополам.
2. Определите взаимное расположение двух плоскостей b и g, если им принадлежат точки B и C. Ответ обоснуйте.
3. Найдите наибольшее число прямых, проходящих через различные пары из 5 точек.
4. Найдите наибольшее число плоскостей, проходящих через различные тройки из четырех точек.
2. Следствия из аксиом стереометрии
1. В плоскости двух пересекающихся прямых a и b задана точка C, не принадлежащая этим прямым. Прямая c, лежащая в данной плоскости, проходит через точку C. Как может быть расположена прямая c относительно данных прямых?
2. Даны три точки, не принадлежащие одной прямой. Докажите, что все прямые, пересекающие два из трех отрезков, соединяющих данные точки, лежат в одной плоскости.
3. Плоскость задана прямой c и не принадлежащей ей точкой C. Постройте в этой плоскости прямую a, отличную от данной прямой и не проходящую через данную точку.
4. Плоскость задана двумя пересекающимися в точке O прямыми a и b. Нарисуйте прямую c, которая пересекает данные прямые и не лежит в данной плоскости.
1. Прямая d, лежащая в плоскости треугольника ABC, пересекает его сторону AB. Каким может быть взаимное расположение прямых d и BC?
2. В плоскости a проведены две параллельные прямые a и b. Докажите, что все прямые, пересекающие данные прямые, лежат в одной плоскости.
3. Плоскость задана двумя пересекающимися в точке O прямыми m и n. Постройте в этой плоскости прямую k, отличную от данных прямых и не проходящую через точку O.
4. Плоскость задана тремя точками D, E, F, не принадлежащими одной прямой. Нарисуйте прямую a, которая пересекает стороны DE и DF треугольника DEF и не лежит в данной плоскости.
3. Пространственные фигуры
1. Нарисуйте пятиугольную призму и разделите ее на тетраэдры.
2. Определите число вершин, ребер и граней: а) куба; б) 7-угольной призмы; в) n-угольной пирамиды.
3. Определите вид призмы, если она имеет: а) 10 вершин; б) 21 ребро; в) 5 граней.
4. Каким образом можно окрасить грани 4-угольной призмы, чтобы соседние (имеющие общее ребро) грани были окрашены в разные цвета? Какое наименьшее число цветов потребуется?
1. Нарисуйте пятиугольную пирамиду и разделите ее на тетраэдры.
2. Определите число вершин, ребер и граней: а) прямоугольного параллелепипеда; б) 6-угольнойной пирамиды; в) n-угольной призмы.
3. Определите вид пирамиды, если она имеет: а) 5 вершин; б) 14 ребер; в) 9 граней.
4. Каким образом можно окрасить грани октаэдра, чтобы соседние (имеющие общее ребро) грани были окрашены в разные цвета. Какое наименьшее число цветов потребуется?
4. Моделирование многогранников
1. Нарисуйте несколько разверток куба.
2. Нарисуйте фигуру, состоящую из четырех равных равносторонних треугольников, не являющуюся разверткой правильного тетраэдра.
3. Нарисуйте развертку правильной четырехугольной пирамиды и раскрасьте ее таким образом, чтобы при склеивании соседние грани имели разные цвета. Какое наименьшее число цветов нужно взять?
4. Нарисуйте развертку прямоугольного параллелепипеда и раскрасьте ее таким образом, чтобы при склеивании соседние грани имели разные цвета. Какое наименьшее число цветов нужно взять?
1. Нарисуйте несколько разверток правильного тетраэдра.
2. Нарисуйте фигуру, состоящую из шести квадратов, не являющуюся разверткой куба.
3. Нарисуйте развертку куба и раскрасьте ее таким образом, чтобы при склеивании соседние грани имели разные цвета. Какое наименьшее число цветов нужно взять?
4. Нарисуйте развертку правильной 6-угольной пирамиды и раскрасьте ее таким образом, чтобы при склеивании соседние грани имели разные цвета. Какое наименьшее число цветов нужно взять?
5. Параллельность прямых в пространстве
1. Запишите в правильной 4-угольнойой пирамиде SABCD все пары параллельных ребер.
2. В плоскости двух параллельных прямых a и b дана точка C, не принадлежащая этим прямым. Через точку C проведена прямая c. Как может быть расположена прямая c относительно прямых a и b.
3. Через точку, не принадлежащую данной прямой, проведите прямую, параллельную данной.
4. Найдите геометрическое место прямых, пересекающих две данные параллельные прямые.
1. Запишите четыре пары параллельных ребер куба A…D1.
2. Даны три прямые a, b и с. Как могут располагаться эти прямые, чтобы можно было провести плоскость, содержащую все данные прямые.
3. Даны две параллельные прямые a и b. Докажите, что любая плоскость, пересекающая одну из них, пересечет и другую.
4. Найдите геометрическое место прямых, параллельных данной прямой и пересекающих другую прямую, пересекающуюся с первой.
6. Скрещивающиеся прямые
1. В кубе A…D1 запишите ребра, скрещивающиеся с ребром AB.
2. Запишите пары скрещивающихся ребер 4-угольной пирамиды SABCD.
3. Как расположены относительно друг друга прямые a и b на рисунке 1? Ответ обоснуйте.
4. Даны две скрещивающиеся прямые a и b и не принадлежащая им точка C. Постройте прямую c, проходящую через точку C и пересекающую прямые a и b.
1. Запишите ребра, скрещивающиеся с ребром SA правильной 4-угольной пирамиды SABCD.
2. Запишите ребра, скрещивающиеся с диагональю B1D куба A…D1.
3. Плоскости a и b пересекаются по прямой c (рис. 1). Прямая a лежит в плоскости a и пересекает прямую c. Можно ли в плоскости b провести прямую, параллельную прямой a? Ответ обоснуйте.
4. Существуют ли две параллельные прямые, каждая из которых пересекает две данные скрещивающиеся прямые? Ответ обоснуйте.
7. Параллельность прямой и плоскости
1. Запишите ребра, параллельные плоскости грани CC1D1D правильной призмы ABCDEFA1B1C1D1E1F1.
2. Прямая a параллельна плоскости a; прямая b пересекает плоскость a в точке B; прямая c, пересекающая прямые a и b соответственно в точках E и F, пересекает плоскость a в точке C. Сделайте рисунок. Как могут располагаться относительно друг друга прямые a и b?
3. Плоскости a и b пересекаются по прямой c. Точка A принадлежит плоскости a, точка B – плоскости b. Постройте: а) прямую a, лежащую в плоскости a, проходящую через точку A и параллельную плоскости b; б) прямую b, лежащую в плоскости b, проходящую через точку B и параллельную плоскости a. Как будут располагаться относительно друг друга прямые a и b?
4. Точки A и B принадлежат смежным боковым граням пирамиды. Проведите в этих гранях через данные точки два отрезка, параллельные между собой.
1. Запишите плоскости граней, параллельных ребру CC1 параллелепипеда A…D1.
2. Прямая a параллельна плоскости a; прямые b и c, пересекающие прямую a соответственно в точках B и C, пересекают плоскость a соответственно в точках D и E. Сделайте рисунок. Как могут располагаться относительно друг друга прямые a и b?
3. Плоскости a и b пересекаются по прямой c. Прямая a лежит в плоскости a. Докажите, что если: а) a пересекает плоскость b в точке A, то A принадлежит прямой c; б) a параллельна плоскости b, то она параллельна прямой c.
4. Точки A и B принадлежат смежным боковым граням призмы. Проведите в этих гранях через данные точки два отрезка, параллельные между собой.
8. Параллельность двух плоскостей
1. Запишите параллельные плоскости параллелепипеда A…D1.
2. Верны ли утверждения:
1) Через точку, не принадлежащую данной плоскости, проходит единственная плоскость, параллельная данной.
2) Если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.
3) Существует бесконечно много прямых, параллельных данной плоскости и проходящих через точку, не принадлежащую этой плоскости.
4) Если одна из двух данных плоскостей параллельна двум пересекающимся прямым, лежащим в другой плоскости, то эти плоскости параллельны.
3. Докажите, что две плоскости, параллельные одной и той же третьей плоскости, параллельны между собой.
4. Отрезки AB и CD лежат соответственно в параллельных плоскостях a и b (рис. 2). Как могут располагаться относительно друг друга прямые AC и BD? Могут ли они быть параллельными?
1. В треугольной пирамиде SABC проведите плоскость, параллельную ее основанию ABC.
2. Верны ли утверждения:
1) Если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.
2) Если плоскость пересекает две данные плоскости по параллельным прямым, то эти плоскости параллельны.
3) Существует бесконечно много плоскостей, параллельных данной прямой и проходящих через точку, не принадлежащую этой прямой.
4) Если две плоскости параллельны одной и той же прямой, то они параллельны.
3. Докажите, что если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
4. Отрезки AB и CD лежат соответственно в параллельных плоскостях a и b (рис. 3). Как могут располагаться относительно друг друга прямые AD и BC? Могут ли они пересекаться?
9. Векторы в пространстве
1. Для данного вектора 



2. Сколько векторов задают всевозможные пары точек, составленные из вершин правильной четырехугольной пирамиды?
3. Изобразите правильный тетраэдр ABCD и нарисуйте вектор: а) 


4. Дан параллелепипед A…D1. Найдите сумму векторов: а) 


1. Для данного вектора 



2. Сколько векторов задают всевозможные пары точек, составленные из вершин треугольной призмы?
3. Изобразите правильный тетраэдр ABCD и нарисуйте вектор: а) 


4. Дан параллелепипед A…D1. Найдите сумму векторов: а) 


10. Коллинеарные и компланарные векторы
1. На какое число нужно умножить ненулевой вектор 



2. Даны два противоположно направленных вектора 





3. Дан тетраэдр ABCD. Запишите три пары его вершин, задающие компланарные векторы.
4. Дан куб A…D1. Запишите тройки некомпланарных векторов с началами и концами в его вершинах.
1. На какое число нужно умножить ненулевой вектор