Доказать что прямые параллельны по координатам (2 видео)

Параллельные прямые, признаки и условия параллельности прямых.

Эта статья о параллельных прямых и о параллельности прямых. Сначала дано определение параллельных прямых на плоскости и в пространстве, введены обозначения, приведены примеры и графические иллюстрации параллельных прямых. Далее разобраны признаки и условия параллельности прямых. В заключении показаны решения характерных задач на доказательство параллельности прямых, которые заданы некоторыми уравнениями прямой в прямоугольной системе координат на плоскости и в трехмерном пространстве.

Навигация по странице.

Содержание

Параллельные прямые – основные сведения.
Параллельность прямых — признаки и условия параллельности.
Параллельность прямых в прямоугольной системе координат.
Условие параллельности прямых
Параллельные прямые, признаки и условия параллельности прямых
Параллельные прямые: основные сведения
Параллельность прямых: признаки и условия параллельности
Параллельность прямых в прямоугольной системе координат
🎬 Видео

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Параллельные прямые – основные сведения.

Напомним сначала определения параллельных прямых, которые были даны в статьях прямая на плоскости и прямая в пространстве.

Две прямые на плоскости называются параллельными, если они не имеют общих точек.

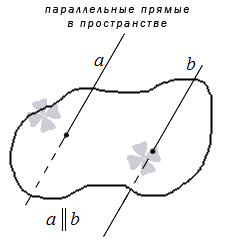
Две прямые в трехмерном пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.

Обратите внимание, что оговорка «если они лежат в одной плоскости» в определении параллельных прямых в пространстве очень важна. Поясним этот момент: две прямые в трехмерном пространстве, которые не имеют общих точек и не лежат в одной плоскости не являются параллельными, а являются скрещивающимися.

Приведем несколько примеров параллельных прямых. Противоположные края тетрадного листа лежат на параллельных прямых. Прямые, по которым плоскость стены дома пересекает плоскости потолка и пола, являются параллельными. Железнодорожные рельсы на ровной местности также можно рассматривать как параллельные прямые.

Для обозначения параллельных прямых используют символ «». То есть, если прямые а и b параллельны, то можно кратко записать а b .

Обратите внимание: если прямые a и b параллельны, то можно сказать, что прямая a параллельна прямой b , а также, что прямая b параллельна прямой a .

Озвучим утверждение, которое играет важную роль при изучении параллельных прямых на плоскости: через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной. Это утверждение принимается как факт (оно не может быть доказано на основе известных аксиом планиметрии), и оно называется аксиомой параллельных прямых.

Для случая в пространстве справедлива теорема: через любую точку пространства, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Эта теорема легко доказывается с помощью приведенной выше аксиомы параллельных прямых (ее доказательство Вы можете найти в учебнике геометрии 10-11 класс, который указан в конце статьи в списке литературы).

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельность прямых — признаки и условия параллельности.

Признаком параллельности прямых является достаточное условие параллельности прямых, то есть, такое условие, выполнение которого гарантирует параллельность прямых. Иными словами, выполнение этого условия достаточно для того, чтобы констатировать факт параллельности прямых.

Также существуют необходимые и достаточные условия параллельности прямых на плоскости и в трехмерном пространстве.

Поясним смысл фразы «необходимое и достаточное условие параллельности прямых».

С достаточным условием параллельности прямых мы уже разобрались. А что же такое «необходимое условие параллельности прямых»? По названию «необходимое» понятно, что выполнение этого условия необходимо для параллельности прямых. Иными словами, если необходимое условие параллельности прямых не выполнено, то прямые не параллельны. Таким образом, необходимое и достаточное условие параллельности прямых – это условие, выполнение которого как необходимо, так и достаточно для параллельности прямых. То есть, с одной стороны это признак параллельности прямых, а с другой стороны – это свойство, которым обладают параллельные прямые.

Прежде чем сформулировать необходимое и достаточное условие параллельности прямых, целесообразно напомнить несколько вспомогательных определений.

Секущая прямая – это прямая, которая пересекает каждую из двух заданных несовпадающих прямых.

При пересечении двух прямых секущей образуются восемь неразвернутых углов. В формулировке необходимого и достаточного условия параллельности прямых участвуют так называемые накрест лежащие, соответственные и односторонние углы. Покажем их на чертеже.

Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180 градусам.

Покажем графическую иллюстрацию этого необходимого и достаточного условия параллельности прямых на плоскости.

Доказательства этих условий параллельности прямых Вы можете найти в учебниках геометрии за 7 — 9 классы.

Заметим, что эти условия можно использовать и в трехмерном пространстве – главное, чтобы две прямые и секущая лежали в одной плоскости.

Приведем еще несколько теорем, которые часто используются при доказательстве параллельности прямых.

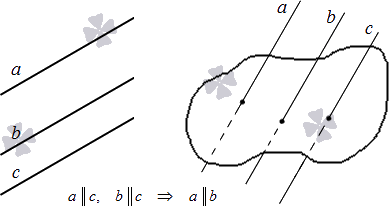
Если две прямые на плоскости параллельны третьей прямой, то они параллельны. Доказательство этого признака следует из аксиомы параллельных прямых.

Существует аналогичное условие параллельности прямых в трехмерном пространстве.

Если две прямые в пространстве параллельны третьей прямой, то они параллельны. Доказательство этого признака рассматривается на уроках геометрии в 10 классе.

Проиллюстрируем озвученные теоремы.

Приведем еще одну теорему, позволяющую доказывать параллельность прямых на плоскости.

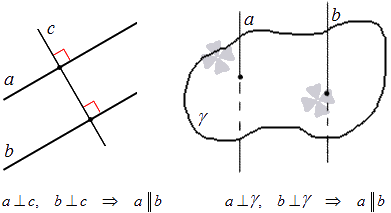
Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.

Существует аналогичная теорема для прямых в пространстве.

Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.

Изобразим рисунки, соответствующие этим теоремам.

Все сформулированные выше теоремы, признаки и необходимые и достаточные условия прекрасно подходят для доказательства параллельности прямых методами геометрии. То есть, чтобы доказать параллельность двух заданных прямых нужно показать, что они параллельны третьей прямой, или показать равенство накрест лежащих углов и т.п. Множество подобных задач решается на уроках геометрии в средней школе. Однако следует отметить, что во многих случаях удобно пользоваться методом координат для доказательства параллельности прямых на плоскости или в трехмерном пространстве. Сформулируем необходимые и достаточные условия параллельности прямых, которые заданы в прямоугольной системе координат.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Параллельность прямых в прямоугольной системе координат.

Если на плоскости задана прямоугольная декартова система координат, то прямую линию в этой системе координат определяет уравнение прямой на плоскости некоторого вида. Аналогично прямую линию в прямоугольной системе координат в трехмерном пространстве задают некоторые уравнения прямой в пространстве.

В этом пункте статьи мы сформулируем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от вида уравнений, определяющих эти прямые, а также приведем подробные решения характерных задач.

Начнем с условия параллельности двух прямых на плоскости в прямоугольной системе координат Oxy . В основе его доказательства лежит определение направляющего вектора прямой и определение нормального вектора прямой на плоскости.

Для параллельности двух несовпадающих прямых на плоскости необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, или нормальные векторы этих прямых были коллинеарны, или направляющий вектор одной прямой был перпендикулярен нормальному вектору второй прямой.

Очевидно, условие параллельности двух прямых на плоскости сводится к условию коллинеарности двух векторов (направляющих векторов прямых или нормальных векторов прямых) или к условию перпендикулярности двух векторов (направляющего вектора одной прямой и нормального вектора второй прямой). Таким образом, если и — направляющие векторы прямых a и b , а и — нормальные векторы прямых a и b соответственно, то необходимое и достаточное условие параллельности прямых а и b запишется как , или , или , где t — некоторое действительное число. В свою очередь координаты направляющих и (или) нормальных векторов прямых a и b находятся по известным уравнениям прямых.

В частности, если прямую a в прямоугольной системе координат Oxy на плоскости задает общее уравнение прямой вида , а прямую b — , то нормальные векторы этих прямых имеют координаты и соответственно, а условие параллельности прямых a и b запишется как .

Если прямой a соответствует уравнение прямой с угловым коэффициентом вида , а прямой b — , то нормальные векторы этих прямых имеют координаты и , а условие параллельности этих прямых примет вид . Следовательно, если прямые на плоскости в прямоугольной системе координат параллельны и могут быть заданы уравнениями прямых с угловыми коэффициентами, то угловые коэффициенты прямых будут равны. И обратно: если несовпадающие прямые на плоскости в прямоугольной системе координат могут быть заданы уравнениями прямой с равными угловыми коэффициентами, то такие прямые параллельны.

Если прямую a и прямую b в прямоугольной системе координат определяют канонические уравнения прямой на плоскости вида и , или параметрические уравнения прямой на плоскости вида и соответственно, то направляющие векторы этих прямых имеют координаты и , а условие параллельности прямых a и b записывается как .

Разберем решения нескольких примеров.

Параллельны ли прямые и ?

Перепишем уравнение прямой в отрезках в виде общего уравнения прямой: . Теперь видно, что — нормальный вектор прямой , а — нормальный вектор прямой . Эти векторы не коллинеарны, так как не существует такого действительного числа t , для которого верно равенство (). Следовательно, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, поэтому, заданные прямые не параллельны.

нет, прямые не параллельны.

Являются ли прямые и параллельными?

Приведем каноническое уравнение прямой к уравнению прямой с угловым коэффициентом: . Очевидно, что уравнения прямых и не одинаковые (в этом случае заданные прямые были бы совпадающими) и угловые коэффициенты прямых равны, следовательно, исходные прямые параллельны.

Второй способ решения.

Сначала покажем, что исходные прямые не совпадают: возьмем любую точку прямой , например, (0, 1) , координаты этой точки не удовлетворяют уравнению прямой , следовательно, прямые не совпадают. Теперь проверим выполнение условия параллельности этих прямых. Нормальный вектор прямой есть вектор , а направляющий вектор прямой есть вектор . Вычислим скалярное произведение векторов и : . Следовательно, векторы и перпендикулярны, значит, выполненяется необходимое и достаточное условие параллельности заданных прямых. Таким образом, прямые параллельны.

заданные прямые параллельны.

Чтобы доказать параллельность прямых в прямоугольной системе координат в трехмерном пространстве пользуются следующим необходимым и достаточным условием.

Для параллельности несовпадающих прямых в трехмерном пространстве необходимо и достаточно, чтобы их направляющие векторы были коллинеарны.

Таким образом, если известны уравнения прямых в прямоугольной системе координат в трехмерном пространстве и нужно ответить на вопрос параллельны эти прямые или нет, то нужно найти координаты направляющих векторов этих прямых и проверить выполнение условия коллинеарности направляющих векторов. Другими словами, если и — направляющие векторы прямых a и b соответственно, то для параллельности прямых a и b необходимо и достаточно, чтобы существовало такое действительное число t , при котором справедливо .

Разберемся с применением условия параллельности прямых в пространстве при решении примера.

Докажите параллельность прямых и .

Нам заданы канонические уравнения прямой в пространстве вида и параметрические уравнения прямой в пространстве вида . Направляющие векторы и заданных прямых имеют координаты и . Так как , то . Таким образом, выполнено необходимое и достаточное условие параллельности двух прямых в пространстве. Этим доказана параллельность прямых и .

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Условие параллельности прямых

Условием параллельности прямых, заданных уравнениями

служит равенство угловых коэффициентов

т. е. прямые параллельны, если их угловые коэффициенты равны, и не параллельны, если угловые коэффициенты не равны. Две совпадающие считаются параллельными.

параллельны, так как у них угловые коэффициенты равны

не параллельны, так как у них угловые коэффициенты не равны

параллельны, так как у них угловые коэффициенты равны

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Видео:Параллельность прямых. 10 класс.Скачать

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Чтобы обозначить параллельность прямых, общепринято использовать символ ∥ . Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b . Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b , или прямая b параллельна прямой а .

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10 — 11 классов).

Видео:Задачи на доказательство по геометрии. Признаки параллельности прямых.Скачать

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

Доказательство указанных условий присутствует в программе геометрии за 7 — 9 классы.

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Видео:Признаки параллельности прямых. Первый. Доказательство.Скачать

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a → = ( a x , a y ) и b → = ( b x , b y ) являются направляющими векторами прямых a и b ;

и n b → = ( n b x , n b y ) являются нормальными векторами прямых a и b , то указанное выше необходимое и достаточное условие запишем так: a → = t · b → ⇔ a x = t · b x a y = t · b y или n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y или a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.

Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A 1 x + B 1 y + C 1 = 0 ; прямая b — A 2 x + B 2 y + C 2 = 0 . Тогда нормальные векторы заданных прямых будут иметь координаты ( А 1 , В 1 ) и ( А 2 , В 2 ) соответственно. Условие параллельности запишем так:

A 1 = t · A 2 B 1 = t · B 2

Прямая a описывается уравнением прямой с угловым коэффициентом вида y = k 1 x + b 1 . Прямая b — y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) соответственно, а условие параллельности запишем так:

k 1 = t · k 2 — 1 = t · ( — 1 ) ⇔ k 1 = t · k 2 t = 1 ⇔ k 1 = k 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x — x 1 a x = y — y 1 a y и x — x 2 b x = y — y 2 b y или параметрическими уравнениями прямой на плоскости: x = x 1 + λ · a x y = y 1 + λ · a y и x = x 2 + λ · b x y = y 2 + λ · b y .

Тогда направляющие векторы заданных прямых будут: a x , a y и b x , b y соответственно, а условие параллельности запишем так:

a x = t · b x a y = t · b y

Заданы две прямые: 2 x — 3 y + 1 = 0 и x 1 2 + y 5 = 1 . Необходимо определить, параллельны ли они.

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y — 1 = 0

Мы видим, что n a → = ( 2 , — 3 ) — нормальный вектор прямой 2 x — 3 y + 1 = 0 , а n b → = 2 , 1 5 — нормальный вектор прямой x 1 2 + y 5 = 1 .

Полученные векторы не являются коллинеарными, т.к. не существует такого значения t , при котором будет верно равенство:

2 = t · 2 — 3 = t · 1 5 ⇔ t = 1 — 3 = t · 1 5 ⇔ t = 1 — 3 = 1 5

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Заданы прямые y = 2 x + 1 и x 1 = y — 4 2 . Параллельны ли они?

Решение

Преобразуем каноническое уравнение прямой x 1 = y — 4 2 к уравнению прямой с угловым коэффициентом:

x 1 = y — 4 2 ⇔ 1 · ( y — 4 ) = 2 x ⇔ y = 2 x + 4

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2 x + 1 , например, ( 0 , 1 ) , координаты этой точки не отвечают уравнению прямой x 1 = y — 4 2 , а значит прямые не совпадают.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Нормальный вектор прямой y = 2 x + 1 это вектор n a → = ( 2 , — 1 ) , а направляющий вектором второй заданной прямой является b → = ( 1 , 2 ) . Скалярное произведение этих векторов равно нулю:

n a → , b → = 2 · 1 + ( — 1 ) · 2 = 0

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t , чтобы выполнялось равенство:

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Заданы прямые x 1 = y — 2 0 = z + 1 — 3 и x = 2 + 2 λ y = 1 z = — 3 — 6 λ . Необходимо доказать параллельность этих прямых.

Решение

Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a → и b → заданных прямых имеют координаты: ( 1 , 0 , — 3 ) и ( 2 , 0 , — 6 ) .

1 = t · 2 0 = t · 0 — 3 = t · — 6 ⇔ t = 1 2 , то a → = 1 2 · b → .

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.