Вращение по окружности на нити (3 видео)

Движение по окружности (кинематика, динамика)

Найти линейную скорость Земли v при ее орбитальном движении. Средний радиус земной орбиты R=1,5·10 8 км.

Ответ и решение

Пропеллер самолета радиусом 1,5 м вращается при посадке с частотой 2000 мин -1 , посадочная скорость самолета относительно Земли равна 162 км/ч. Определить скорость точки на конце пропеллера. Какова траектория движения этой точки?

Ответ и решение

v ≈ 317 м/с. Точка на конце пропеллера описывает винтовую линию с шагом h ≈ 1,35 м.

Пропеллер самолета вращается с частотой:

λ = 2000/60 с -1 = 33,33 с -1 .

Линейная скорость точки на конце пропеллера:

Скорость самолета при посадке v = 45 м/с.

Результирующая скорость точки на конце пропеллера равна сумме векторов линейной скорости при вращении пропеллера и скорости самолета при посадке:

v_рез = ≈ 317 м/с.

Шаг винтовой траектории равен:

Диск радиусом R катится без скольжения с постоянной скоростью v. Найти геометрическое место точек на диске, которые в данный момент имеют скорость v.

Геометрическим местом точек на диске, имеющих скорость v в данный момент, является дуга радиуса R, центр которой лежит в точке касания диска с плоскостью, т.е. в мгновенном центре вращения.

Цилиндрический каток радиусом R помещен между двумя параллельными рейками. Рейки движутся в одну сторону со скоростями v₁ и v₂.

Определить угловую скорость вращения катка и скорость его центра, если проскальзывание отсутствует. Решить задачу для случая, когда скорости реек направлены в разные стороны.

; .

По горизонтальной плоскости катится без скольжения с постоянной скоростью v_c обруч радиусом R. Каковы скорости и ускорения различных точек обруча относительно Земли? Выразить скорость как функцию угла между вертикалью и прямой, проведенной между точкой прикосновения обруча с плоскостью и данной точкой обруча.

v_A = 2v_Ccosα. Ускорение точек обода содержит только центростремительную составляющую, равную a_ц = v 2 /R.

Автомобиль движется со скоростью v = 60 км/ч. С какой частотой n вращаются его колеса, если они катятся по шоссе без скольжения, а внешний диаметр покрышек колес равен d = 60 см? Найти центростремительное ускорение а_цс внешнего слоя резины на покрышках его колес.

На горизонтальную плоскость кладут тонкостенный цилиндр, вращающийся со скоростью v₀ вокруг своей оси. Какой будет скорость движения оси цилиндра, когда прекратится проскальзывание цилиндра относительно плоскости?

Совершает ли работу равнодействующая всех сил, приложенных к телу, равномерно движущемуся по окружности?

Груз массой m может скользить без трения по горизонтальному стержню, вращающемуся вокруг вертикальной оси, проходящей через один из его концов. Груз соединяют с этим концом стержня пружиной, коэффициент упругости которой k. При какой угловой скорости ω пружина растянется на 50% первоначальной длины?

Две точечные массы m₁ и m₂ прикреплены к нити и находятся на абсолютно гладком столе. Расстояния от них до закрепленного конца нити равны l₁ и l₂ соответственно.

Система вращается в горизонтальной плоскости вокруг оси, проходящей через закрепленный конец, с угловой скоростью ω. Найти силы натяжения участков нити Т₁ и Т₂.

Человек сидит на краю круглой горизонтальной платформы радиусом R=4 м. С какой частотой n должна вращаться платформа вокруг вертикальной оси, чтобы человек не мог удержаться на ней при коэффициенте трения k=0,27?

Тело массой m находится на горизонтальном диске на расстоянии r от оси. Диск начинает раскручиваться с малым ускорением. Построить график зависимости составляющей силы трения в радиальном направлении, действующей на тело, от угловой скорости вращения диска. При каком значении угловой скорости диска начнется соскальзывание тела?

Камень массой m=0,5 кг, привязанный к веревке длиной l=50 см, вращается в вертикальной плоскости. Сила натяжения веревки, когда камень проходит низшую точку окружности, Т=44 Н. На какую высоту h над нижней точкой окружности поднимется камень, если веревку перерезать в тот момент, когда его скорость направлена вертикально вверх?

Спортсмен посылает молот (ядро на тросике) на расстояние l=70 м по траектории, обеспечивающей максимальную дальность броска. Какая сила Т действует на руки спортсмена в момент броска? Масса молота m=5 кг. Считать, что спортсмен разгоняет молот, вращая его в вертикальной плоскости по окружности радиусом R=1,5 м. Сопротивление воздуха не учитывать.

Автомобиль массой М=3*10 3 кг движется с постоянной скоростью v=36 км/ч: а) по горизонтальному мосту; б) по выпуклому мосту; в) по вогнутому мосту. Радиус кривизны моста в последних двух случаях R=60 м. С какой силой давит автомобиль на мост (в последних двух случаях) в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α=10° с вертикалью?

По выпуклому мосту, радиус кривизны которого R = 90 м, со скоростью v = 54 км/ч движется автомобиль массой m = 2 т. В точке моста, направление на которую из центра кривизны моста составляет с направлением на вершину моста угол α, автомобиль давит с силой F = 14 400 Н. Определить угол α.

Шарик массой m = 100 г подвешен на нити длиной l =1 м. Шарик раскрутили так, что он начал двигаться по окружности в горизонтальной плоскости. При этом угол, составляемый нитью с вертикалью, α = 60°. Определить полную работу, совершаемую при раскручивании шарика.

С какой наибольшей скоростью может двигаться автомобиль на повороте с радиусом закругления R = 150 м, чтобы его не «занесло», если коэффициент трения скольжения шин о дорогу k = 0,42?

1. Каким должен быть максимальный коэффициент трения скольжения k между шинами автомобиля и асфальтом, чтобы автомобиль мог пройти закругление радиусом R = 200 м при скорости v = 100 км/ч?

2. Автомобиль со всеми ведущими колесами, трогаясь с места, равномерно набирает скорость, двигаясь по горизонтальному участку дороги, представляющему собой дугу окружности α = 30° радиусом R = 100 м. С какой максимальной скоростью автомобиль может выехать на прямой участок пути? Коэффициент трения колес о землю k = 0,3.

Поезд движется по закруглению радиусом R = 800 м со скоростью v = 12 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего, чтобы на колесах не возникало бокового усилия. Расстояние между рельсами по горизонтали принять равным d = 1,5 м.

Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте?

1. С какой максимальной скоростью v может ехать по горизонтальной плоскости мотоциклист, описывая дугу радиусом R = 90 м, если коэффициент трения скольжения k = 0,4?

2. На какой угол φ от вертикального направления он должен при этом отклониться?

3. Чему будет равна максимальная скорость мотоциклиста, если он будет ехать по наклонному треку с углом наклона α = 30° при том же радиусе закругления и коэффициенте трения?

4. Каким должен быть угол наклона трека α₀ для того, чтобы скорость мотоциклиста могла быть сколь угодно большой?

Самолет совершает поворот, двигаясь по дуге окружности с постоянной скоростью v = 360 км/ч. Определить радиус R этой окружности, если корпус самолета повернут вокруг направления полета на угол α = 10°.

На повороте дороги радиусом R = 100 м равномерно движется автомобиль. Центр тяжести автомобиля находится на высоте h = 1 м, ширина колеи автомобиля а = 1,5 м. Определить скорость v, при которой автомобиль может опрокинуться. В поперечном направлении автомобиль не скользит.

Шофер, едущий на автомобиле, внезапно заметил впереди себя забор, перпендикулярный направлению его движения. Что выгоднее сделать, чтобы предотвратить аварию: затормозить или повернуть в сторону?

В вагоне поезда, идущего равномерно по криволинейному пути со скоростью v = 12 км/ч, производится взвешивание груза на пружинных весах. Масса груза m = 5 кг, а радиус закругления пути R = 200 м. Определить показание пружинных весов (силу натяжения пружины Т).

Найти силу F_ед.об., отделяющую сливки (плотность ρ_с = 0,93 г/см 3 ) от снятого молока (ρ_м = 1,03 г/см 3 ) в расчете на единицу объема, если отделение происходит: а) в неподвижном сосуде; б) в центробежном сепараторе, вращающемся с частотой 6000 мин -1 , если жидкость находится на расстоянии r = 10 см от оси вращения.

Самолет делает «мертвую петлю» с радиусом R = 100 м и движется по ней со скоростью v = 280 км/ч. С какой силой F тело летчика массой М = 80 кг будет давить на сиденье самолета в верхней и нижней точках петли?

Определить силу натяжения Т каната гигантских шагов, если масса человека М = 70 кг и канат при вращении образует со столбом угол α = 45°. С какой угловой скоростью со будут вращаться гигантские шаги, если длина подвеса l = 5 м?

T ≈ 990 Н; ω ≈ 1,68 рад/с.

Найти период Т вращения маятника, совершающего круговые движения в горизонтальной плоскости. Длина нити l. Угол, образуемый нитью с вертикалью, α.

Грузик, подвешенный на нити, вращается в горизонтальной плоскости так, что расстояние от точки подвеса до плоскости, в которой происходит вращение, равно h. Найти частоту и вращения груза, считая ее неизменной.

. Результат не зависит от длины подвеса.

Люстра массой m = 100 кг подвешена к потолку на металлической цепи, длина которой l = 5 м. Определить высоту h, на которую можно отклонить люстру, чтобы при последующих качениях цепь не оборвалась? Известно, что разрыв цепи наступает при силе натяжения Т > 1960 Н.

Шарик массой m подвешен на нерастяжимой нити. На какой минимальный угол α_мин надо отклонить шарик, чтобы при дальнейшем движении нить оборвалась, если максимально возможная сила натяжения нити 1,5 mg?

Маятник отклоняют в горизонтальное положение и отпускают. При каком угле α с вертикалью сила натяжения нити будет равна по величине действующей на маятник силе тяжести? Маятник считать математическим.

Груз массой m, привязанный к нерастяжимой нити, вращается в вертикальной плоскости. Найти максимальную разность сил натяжений нити.

Гимнаст «крутит солнце» на перекладине. Масса гимнаста m. Считая, что вся его масса сосредоточена в центре тяжести, а скорость в верхней точке равна нулю, определить силу, действующую на руки гимнаста в нижней точке.

Один грузик подвешен на нерастяжимой нити длиной l, а другой — на жестком невесомом стержне такой же длины. Какие минимальные скорости нужно сообщить этим грузикам, чтобы они вращались в вертикальной плоскости?

Для нити v_мин = ; для стержня v_мин = .

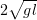
Шарик массой М подвешен на нити. В натянутом состоянии нить расположили горизонтально и отпустили шарик. Вывести зависимость силы натяжения нити Т от угла α, который образует в данный момент нить с горизонтальным направлением. Проверить выведенную формулу, решив задачу для случая прохождения шарика через положение равновесия, при α = 90°.

Математический маятник длиной l и массой М отвели на угол φ₀ от положения равновесия и сообщили ему начальную скорость v₀, направленную перпендикулярно к нити вверх. Найти силу натяжения нити маятника Т в зависимости от угла φ нити с вертикалью.

Грузик, подвешенный на нити, отводят в сторону так, что нить принимает горизонтальное положение, и отпускают. Какой угол с вертикалью α образует пить в тот момент, когда вертикальная составляющая скорости грузика наибольшая?

Одинаковые упругие шарики массой m, подвешенные на нитях равной длины к одному крючку, отклоняют в разные стороны от вертикали на угол α и отпускают. Шарики ударяются и отскакивают друг от друга. Какова сила F, действующая на крючок: а) при крайних положениях нитей; б) в начальный и конечный моменты удара шариков; в) в момент наибольшей деформации шариков?

Математическому маятнику с гибкой нерастяжимой нитью длиной l сообщают из положения равновесия горизонтальную скорость v₀. Определить максимальную высоту его подъема h при движении по окружности, если v₀ 2 = 3gl. По какой траектории будет двигаться шарик маятника после того, как он достиг максимальной высоты подъема h на окружности? Определить максимальную высоту H, достигаемую при этом движении маятника.

; по параболе; .

Маленький шарик подвешен в точке А на нити длиной l. В точке О на расстоянии l/2 ниже точки А в стену вбит гвоздь. Шарик отводят так, что нить занимает горизонтальное положение, и отпускают. В какой точке траектории исчезает сила натяжения нити? Как дальше будет двигаться шарик? До какой наивысшей точки поднимется шарик?

На l/6 ниже точки подвеса; по параболе; на 2l/27 ниже точки подвеса.

Сосуд, имеющий форму расширяющегося усеченного конуса с диаметром дна D = 20 см и углом наклона стенок α = 60°, вращается вокруг вертикальной оси 00₁. При какой угловой скорости вращения сосуда ω маленький шарик, лежащий на его дне, будет выброшен из сосуда? Трение не учитывать.

Сфера радиусом R = 2 м равномерно вращается вокруг оси симметрии с частотой 30 мин -1 . Внутри сферы находится шарик массой m = 0,2 кг. Найти высоту h, соответствующую положению равновесия шарика относительно сферы, и реакцию сферы N.

Внутри конической поверхности, движущейся с ускорением a, вращается шарик по окружности радиусом R. Определить период Т движения шарика по окружности. Угол при вершине конуса 2α.

Небольшое тело массой m соскальзывает вниз по наклонному скату, переходящему в мертвую петлю радиусом R.

Трение ничтожно мало. Определить: а) какова должна быть наименьшая высота h ската, чтобы тело сделало полную петлю, не выпадая; б) какое давление F при этом производит тело на помост в точке, радиус-вектор которой составляет угол α с вертикалью.

Лента конвейера наклонена к горизонту под углом α. Определить минимальную скорость ленты v_мин, при которой частица руды, лежащая на ней, отделяется от поверхности ленты в месте набегания ее на барабан, если радиус барабана равен R.

v_мин = .

Небольшое тело скользит с вершины сферы вниз. На какой высоте h от вершины тело оторвется от поверхности сферы радиусом R? Трением пренебречь.

Найти кинетическую энергию обруча массой m, катящегося со скоростью v. Проскальзывания нет.

Тонкий обруч без проскальзывания скатывается в яму, имеющую форму полусферы. На какой глубине h сила нормального давления обруча на стенку ямы равна его силе тяжести? Радиус ямы R, радиус обруча r.

Маленький обруч катится без скольжения по внутренней поверхности большой полусферы. В начальный момент у ее верхнего края обруч покоился. Определить: а) кинетическую энергию обруча в нижней точке полусферы; б) какая доля кинетической энергии приходится на вращательное движение обруча вокруг его оси; в) нормальную силу, прижимающую обод к нижней точке полусферы. Масса обруча равна m, радиус полусферы R.

Вода течет по трубе, расположенной в горизонтальной плоскости и имеющей закругление радиусом R = 2 м. Найти боковое давление воды. Диаметр трубы d = 20 см. Через поперечное сечение трубы в течение одного часа протекает М = 300 т воды.

Тело соскальзывает из точки А в точку В по двум искривленным наклонным поверхностям, проходящим через точки A и В один раз по выпуклой дуге, второй — по вогнутой. Обе дуги имеют одинаковую кривизну и коэффициент трения в обоих случаях один и тот же.

В каком случае скорость тела в точке B больше?

В случае движения по выпуклой дуге.

Стержень ничтожной массы длиной l с двумя маленькими шариками m₁ и m₂ (m₁ > m₂) на концах может вращаться около оси, проходящей через середину стержня перпендикулярно к нему. Стержень приводят в горизонтальное положение и отпускают. Определить угловую скорость ω и силу давления F на ось в момент прохождения стержнем с шариками положения равновесия.

; .

На виток цилиндрической спирали, ось которой вертикальна, надевают маленькое колечко массой m. Колечко без трения начинает скользить по спирали. С какой силой F будет колечко давить на спираль после того, как оно пройдет n полных витков? Радиус витка R, расстояние между соседними витками h (шаг витка). Считать h ≪ R.

Замкнутая металлическая цепочка лежит на гладхом горизонтальном диске, будучи свободно насажена на центрирующее ее кольцо, соосное с диском. Диск приведен во вращение. Принимая форму цепочки за горизонтальную окружность, определить силу натяжения Т вдоль цепочки, если ее масса m = 150 г, длина l = 20 см и цепочка вращается с частотой n = 20 с -1 .

Реактивный самолет m = 30 т летит вдоль экватора с запада на восток со скоростью v = 1800 км/ч. На сколько изменится подъемная сила, действующая на самолет, если он будет лететь с той же скоростью с востока на запад?

Содержание

Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности
Условие задачи:
Решение задачи:
Ответ: 4,5 рад/с.
Шарик на нити длиной I равномерно движется по окружности в горизонтальной плоскости При этом нить все время образует с вертикалью угол
Ваш ответ
решение вопроса
Похожие вопросы
📹 Видео

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности

Видео:Физика - движение по окружностиСкачать

Условие задачи:

Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности в горизонтальной плоскости. Найти угловую скорость вращения груза, если при его вращении нить отклонена от вертикали на угол 60°? ((g=9,8) м/с 2 )

Задача №2.4.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

(l=98) см, (alpha=60^circ), (g=9,8) м/с 2 , (omega-?)

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Решение задачи:

На схеме покажем груз, действующие на него силы и геометрические параметры задачи. Груз покоится относительно оси (y), что дает нам право применить первый закон Ньютона в проекции на ось (y):

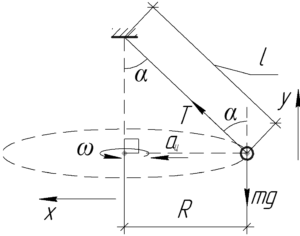
[T cdot cos alpha = mg;;;;(1)]

Так как груз в горизонтальной плоскости равномерно движется по окружности некоторого радиуса (R), то запишем второй закон Ньютона в проекции на ось (x):

[T cdot sin alpha = m]

Поскольку нам нужно найти угловую скорость вращения (omega), то запишем такую формулу определения ускорения (a_ц):

Поделим полученное равенство (2) на равенство (1):

Из прямоугольного треугольника с катетом (R), гипотенузой (l) и углом (alpha) верно, что:

[R = l cdot sin alpha ]

[tgalpha = frac<<l cdot sin alpha >>]

Переведем длину нити в единицы системы СИ, далее посчитаем численный ответ задачи.

Видео:Вращение по окружности, нормальное ускорение Скачать