Построить три проекции прямой призмы с параллельными основаниями нижнее abc и верхнее высотой 50мм

http://espe.spb.ru понятие механизм.

Построить три проекции призмы

S (АВС l), S || П2, m Ì S .

Призма S (АВС,l) – фронтально проецирующая. Ребра l ^ П2 и || П1, П3

1. Достроить проекции призмы на П1 и на П3 (линия обреза А ¢ В ¢ С ¢ )

2. m Ì S -ломаная линия, состоит из двух прямых, которые обозначим тремя точками (1,2,3).

3. На П2 проекции призмы и линии m совпадают.

4. На П3 точки 13 и 23 будут видимыми, так как лежат в плоскости АА′В ¢ В, расположенной ближе к наблюдателю (т.е. левее, чем ВВ ¢ С ¢ С)

5. Точка 33 расположена в плоскости ВВ’СС’ , которая на П3 закрыта плоскостями АА’В ¢ В и АА’С ¢ С, следовательно, будет невидимой (рис.22.2)

6. Соединим три точки, с учетом видимости, получим профильную проекцию линии m.

Построить три проекции цилиндра вращения

Q (i,l), если Q || П1;

Цилиндр вращения Q — горизонтально проецирующий.Образующая

l ^ П1 и || П2, || П3.

1. Построить проекции цилиндра на П1, П2, П3.

2. Кривая n Ì Q . Возьмем на фронтальной проекции кривой 5 произвольных точек. Точки 32 и 52 — особые, находятся на крайних образующих; 12, 22, 42 — промежуточные точки.

3. На П1 все точки совпадают с проекцией цилиндра вращения.

4. Находим проекции точек на П3. Точки 13, 23, 33 будут видимыми, а точки 43, 53 — невидимыми. Точки 33 и 53 не требуют дополнительных построений, т.к. они уже лежат на своих образующих (рисю23.2).

5. Соединив точки на П3 с учетом видимости, получим профильную проекцию кривой n3 (рис.23.2).

Построить проекции трехгранной призмы Ф(АВС, s), М Î Ф , М1 = ? Высота призмы 40 мм

Вспомним алгоритм конструирования поверхности (тема 2. Что задано на чертеже?

Проекции геометрической части определителя. Строим дискретный каркас, закон каркаса:

С какой проекции начнем конструировать линейчатую поверхность? Можно начать с любой, но, учитывая условие задачи (высота 40 мм), начнем построение с фронтальной проекции, проведя 3 образующие || s2.

Построить проекции линии обреза на П2

А2’В2’С2’ — фронтальная проекция линии обреза. С помощью линий связи построить ее горизонтальную проекцию – А1’В1’С1’

Для того, чтобы обвести проекции поверхности основной сплошной линией, необходимо определить видимость.

Точки 1 = 2(11 = 21)-горизонтально конкурирующие, точка 1 выше, чем точка 2.

Точки В’ = 4(В2’ = 42) — фронтально конкурирующие, точка В ¢ ближе к наблюдателю, чем точка 4.

Ребро В1В1’ частично видимо, т.к. поверхность (в данном случае призма) — это пустотелая геометрическая фигура., имеющая только боковую поверхность.

На П2 точка М(М2)- видимая, Î АА’В ¢ В. Через точку М(М2) провести образующую М5(М252). Точка М(М1) – невидимая (рис.24.5).

Вторая основная метрическая задача (2 ОМЗ)

(перпендикулярность прямой и плоскости)

Решение основано на признаке перпендикулярности прямой и плоскости.

Прямая, перпендикулярна к плоскости, если она одновременно перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости.

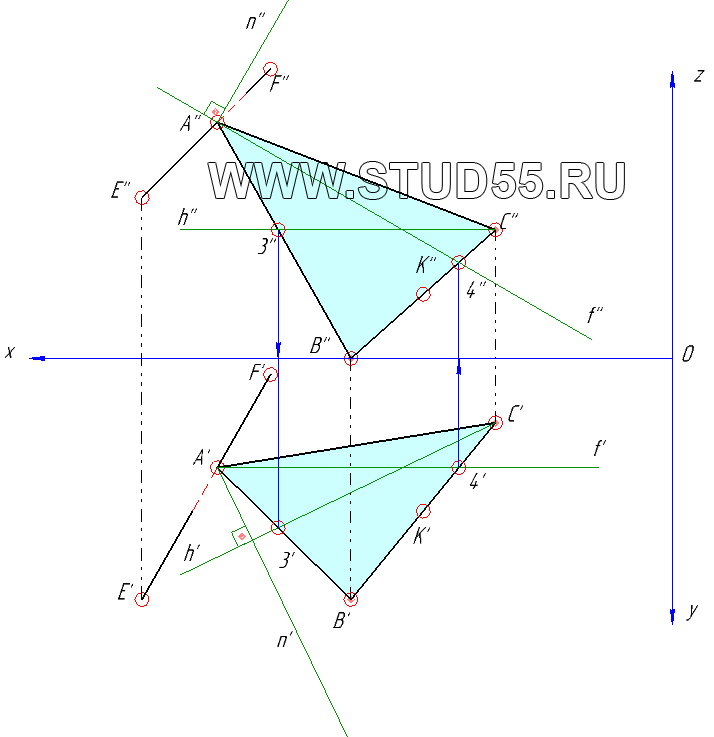
Пример. На комплексном чертеже (Рис.54) двумя своими проекциями (А1В1С1 и А2В2С2) задана плоскость S (АВС).

Видео:Построение проекции пирамиды. Метод прямого треугольника.Скачать

Построить три проекции прямой призмы с параллельными основаниями нижнее abc и верхнее высотой 50мм

Видео:Построение призмы высотой 30ммСкачать

Пошаговое решение метрической задачи по начертательной геометрии МГТУ им. Баумана

Видео:Построение изометрии шестигранной призмыСкачать

Задача 2 (вариант 19)

ПОСТРОИТЬ ПРОЕКЦИИ ПРЯМОЙ ПРИЗМЫ АВСА₁В₁С₁,

при условии, что её высота равна 70 мм., а в основании лежит равнобедренный треугольник ABC (АВ=АС) с вершиной А на прямой EF.

Решить без преобразования чертежа.

Видео:Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

Решение задачи по начертательной геометрии:

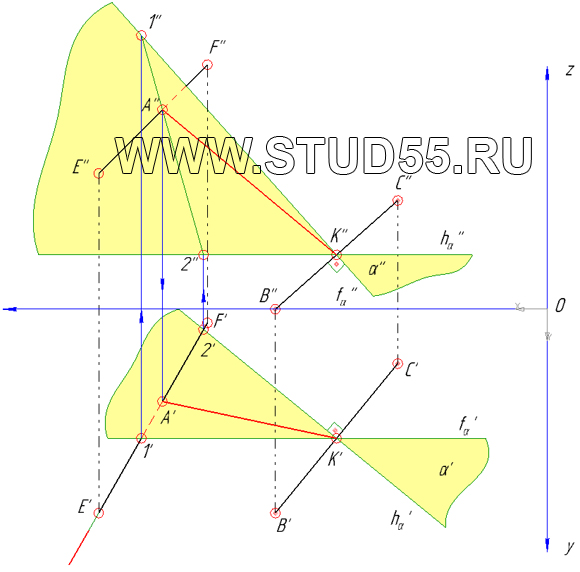
1) Проекции точки К получаем просто разделив СВ на 2 равные части: СК=КВ

2) Далее нам необходимо построить плоскость a (альфа) перпендикулярную отрезку СВ в точке К,

СВ занимает общее положение в пространстве, поэтому начать ее построение можно в горизонтальной плоскости проекций,

для этого проводим через точку К — фронтальный луч f ‘ параллельно х и горизонтальный h ‘ перпенд. С’K’

Следовательно, во фронтальной плоскости проекций искомая плоскость альфа будет задана лучами f » перпенд. С»K» и

горизонтальным h ‘» параллельным оси х.

3) Теперь мы можем определить точку А пересечения построенной плоскости альфа с отрезком EF. Для этого через EF (E’F’)

проводим горизонтально проецирующую плоскость перпендикулярную горизонт. плоскости проекций, отмечаем на лучах

проекции f ‘ точку — 1′ и на h ‘ — 2′. По линиям связи переносим на фронтальную плоскость и получаем фронтальную проекцию

отрезка 1-2 (1»2»).

4) В точке пересечения 1»2» и E»F» — находим проекцию точки пересечения плоскости альфа и EF — A», по линии связи находим

горизонтальную проекцию точки А (A’).

5) Если соединить точки А и К, то получим отрезок АК, который будет принадлежать плоскости альфа, Т.к. он принадлежит

плоскости альфа и альфа перпендикулярна СВ, следовательно,

и отрезок АК будет перпендикулярен СВ. Следовательно отрезки АС и СВ будут равноудалены от точки А и мы находим

основание нашей призмы в основании которой будет равнобедренный треугольник АВС с АС=АВ.

6) Т.к. призма прямая, следовательно, ребра призмы должны быть перпедикулярны основанию АВС. Построим перпендикуляр n к АВС из точки А, для

этого проведем фронталь f и горизонталь h плоскости АВС. Далее строим n’ перпенд. h’ и n» перпенд. f».

7) Далее нам необходимо на перпендикуляре n отложить ребро АА₁₀=70 мм. Для этого на n возьмем произвольную точку H — H» и H’, и определим натуральную величину отрезка АН способом прямоугольного треугольника, для этого из проекции H’ под прямым углом к n’ отложим разницу высот точек А и Н. На A’H₀ — будет натуральной величиной отрезка АН.

8) На A’H откладываем отрезок равный 70 мм от А’ и по линии связи находим вершину призмы A₁‘, получаем проекцию ребра A’A’₁, и по линии связи на n» получаем A₁‘’ — и ребро A»A₁»

9) Достраиваем ребра, получаем 2 проекции нашей искомой призмы. С помощью 2-ух пар конкурирующих точек 5 6 и 7 8, определяем видимость всех ребер призмы.

Видео:Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Проекции геометрических тел с примерами и образцами выполнения

Содержание:

Формы деталей, встречающихся в технике, представляют собой сочетание различных геометрических тел или их частей.

Видео:Построить проекции линии и точек на ней по заданным координатам. Начертательная геометрияСкачать

Формы геометрических тел

Деталь любой формы можно представить как совокупность отдельных геометрических тел.

Для примера возьмем деталь (рис. 159. а) и проанализируем се форму. Мысленно разделив ее на отдельные элементы, получим следующие гео­метрические тела (рис. 159, б): 1 — усеченный прямой круговой конус с цилиндрическим отвер­стием, 2 — прямой круговой цилиндр, 3 — прямо­угольный параллелепипед, 4 — два прямоугольных параллелепипеда с цилиндрическими отверстия­ми, 5 — два полых полуцилиндра. Для выполне­ния комплексных чертежей необходимо усвоить методы проецирования отдельных геометрических тел, а также точек и линий, расположенных на поверхности этих тел.

Геометрические тела, ограниченные плоскими многоугольниками, называются многогранниками (рис. 160, а). Эти многоугольники называются гранями, их пересечения — ребрами. Угол, образо­ванный гранями, сходящимися в одной точке — вершине, называется многогранным углом.

Тела вращения ограничены поверхностями, которые получаются в результате вращения ка­кой-либо линии вокруг неподвижной оси (рис. 160, б и в). Линия АВ, которая при своем движении образует поверхность, называется обра­зующей. Наиболее часто встречаются такие тела вращения, как цилиндр, конус, шар, тор.

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Проекции призм

Построение проекций правильной прямой шес­тиугольной призмы (рис. 161) начинается с выпо­лнения ее горизонтальной проекции — правильно­го шестиугольника. Из вершин этого шестиуголь­ника провопят вертикальные линии связи и строят фронтальную проекцию нижнего основания при­змы. Эта проекция изображается отрезком гори­зонтальной прямой. От этой прямой вверх откла­дывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчива­ют фронтальные проекции ребер — отрезки верти­кальных прямых, равные высоте призмы. Фрон­тальные проекции передних и задних ребер совпа­дают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых. Передняя боковая грань 1243 изображается на плоскости V без искажения, а на плоскости W— в виде прямой линии. Фронтальные и профильные проекции остальных боковых граней изображаются с иска­жением.

На чертеже оси х, у и z не показывают, что делает чертеж более простым.

Несколько сложнее построение проекций на­клонной призмы.

Рассмотрим порядок построения проекций на­клонной шестиугольной призмы.

1. Призма, основание которой лежит на плос­кости Н, наклонена к этой плоскости под утлом α (рис. 162, а). Ребра призмы параллельны плоскос­ти V, т.е. являются фронталями.

Вначале выполняется построение горизонталь­ной проекции основания призмы, которое проеци­руется на плоскость Н без искажения (правиль­ный шестиугольник). Фронтальная проекция осно­вания представляет собой отрезок прямой, парал­лельной оси х.

Из точек 1‘, 2′, 3’ фронтальной проекции основания проводят прямые проекции ребер под углом α к оси х и на них откладывают действи­тельную длину бокового ребра призмы.

Строят фронтальную проекцию верхнего осно­вания призмы в виде отрезка прямой, равного и параллельного фронтальной проекции нижнего основания.

Из точек 1, 2, 3, 4. 5. 6 горизонтальной проек­ции нижнего основания проводят прямые — про­екции ребер — параллельно оси х и на них с по­мощью вертикальных линий связи находят шесть точек — горизонтальные проекции вершин верхне­го основания призмы.

2. Прямая правильная шестиугольная призма наклонена под углом α к плоскости Н. Основание призмы наклонено к плоскости Н под углом β (рис. 162, б).

В этом случае необходимо вначале построить фронтальную проекцию основания. Эта проекция представляет собой отрезок, равный расстоянию между параллельными сторонами шестиугольника. Если этот отрезок разделить пополам и из его середины провести линию связи, то на ней будут расположены точки 2 и 5 — горизонтальные про­екции вершин основания призмы. Расстояние между точками 2, 5 равно действительному рас­стоянию между вершинами основания призмы. Так как горизонтальные проекции сторон 16 и 34 представляют собой их действительные длины, то, воспользовавшись этим обстоятельством, мож­но построить полностью горизонтальную проек­цию основания.

Дальнейший процесс построения, показанный на рис. 162, б, аналогичен приведенному на рис. 162, а.

На комплексных чертежах предметов часто приходится строить проекции линий и точек, расположенных на поверхности этих тел, имея только одну проекцию линии или точки. Рассмотрим решение такой задачи.

Дан комплексный чертеж четырехугольной пря­мой призмы и фронтальная проекция а’ точки А.

Прежде всего надо отыскать на комплексном чертеже две проекции грани, на которой располо­жена точка А. На комплексном чертеже видно (рис. 163, а), что точка А лежит на грани призмы 1265. Фронтальная проекция а’ точки А лежит на фронтальной проекции 1‘2’6’5‘ грани призмы. Горизонтальная проекция 1562 этой грани — отре­зок 56. На этом отрезке и находится горизонталь­ная проекция а точки А. Профильную проекцию призмы и точки А строят, применяя линии связи.

По имеющемуся комплексному чертежу призмы можно выполнить ее изометрическую проекцию по координатам вершин. Для этого вначале строят нижнее основание призмы (рис. 163, б), а затем вертикальные ребра и верхнее основание (рис. 163, в).

По координатам т и п точки А, взятым с ком­плексного чертежа, можно построить аксономет­рическую проекцию этой точки.

Видео:ЗАДАЧИ ПО ОСНОВАМ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ. МЕТОДЫ ПРОЕЦИРОВАНИЯ И ЭПЮРЫ ТОЧЕК. №1Скачать

Проекции пирамид

Построение проекций треугольной пирамиды начинается с построения основания, горизонталь­ная проекция которого представляет собой тре­угольник без искажения (рис. 164, а). фронталь­ная проекция основания — отрезок горизонталь­ной прямой.

Из горизонтальной проекции точки s (верши­ны. пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию s’ вершины. Соединяя точку s’ с точками 1‘, 2′ и 3′, получают фронтальные проекции ребер пира­миды.

Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки s с горизонтальными проекциями точек 1, 2 и 3.

Пусть, например, дана фронтальная проекция а’ точки А, расположенной на грани пирамиды 1s2, и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через а’ произвольную вспомогательную прямую и продолжим ее до пересечения с фронтальными проекциями 1’s’ и 2’s’ ребер в точках п’ и т‘. Затем проведем из точек п’ и т‘ линии связи до пересечения с горизонтальными проекциями 1s и 2s этих ребер в точках п и т. Соединив п с т, получим горизонтальную проекцию вспомогательной прямой, на которой с помощью линии связи найдем искомую горизонтальную проекцию а точки А Профильную проекцию этой точки нахо­дят по линиям связи.

Другой способ решения задачи на построение проекции точки по заданной ее проекции показан на рис. 164, б. Дана четырехугольная правильная пирамида. Через заданную фронтальную проек­цию а’ точки А проводят вспомогательную пря­мую, проходящую через вершину пирамиды и расположенную на ее грани. Горизонтальную проекцию ns вспомогательной прямой находят с помощью линии связи. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, проведенной из точки а’, с горизон­тальной проекцией ns вспомогательной прямой.

Фронтальная диметрическая проекция рассмат­риваемой пирамиды выполняется следующим образом (рис. 164, в).

Вначале строят основание, для чего по оси х откладывают длину диагонали 13, а по оси у — половину длины диагонали 24. Из точки О пере­сечения диагоналей проводят ось z и на ней от­кладывают высоту пирамиды. Вершину S соединя­ют с вершинами основания прямыми линиями — ребрами.

Фронтальную диметрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чер­тежа. От качала координат О по оси х отклады­вают координату x_А, из се конца параллельно оси у — половину координаты y_А и из конца этой ко­ординаты параллельно оси z — третью координату z_А. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х от­кладывают координату x_B и из конца ее проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.

Видео:Начертательная геометрия 1 курс. Построить проекции пирамидыСкачать

Проекции цилиндров

Боковая поверхность прямого кругового цилин­дра получается вращением отрезка АВ образую­щей вокруг оси, параллельной этому отрезку. На рис. 165, а представлена изометрическая проекция цилиндра.

Построение горизонтальной и фронтальной проекций цилиндра показано на рис. 165, б и в.

Построение начинают с изображения основания цилиндра, т.е. двух проекций окружности (рис. 165, б). Так как окружность расположена на плоскости Н, то она проецируется на эту плос­кость без искажения. Фронтальная проекция ок­ружности представляет собой отрезок горизон­тальной прямой линии, равный диаметру окруж­ности основания.

После построения основания на фронтальной проекции проводят две очерковые (крайние) обра­зующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, кото­рый является фронтальной проекцией верхнего основания цилиндра (рис. 165, в).

Определение недостающих проекции точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном слу­чае затруднений нс вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рис. 166. а). Следовательно, горизонтальные проекции точек А и В можно найти, проводя из данных точек а’ и b‘ вертикальные линии связи до их пересечения с окружностью в искомых точ­ках а и Ь.

Профильные проекции точек А и В строят так­же с помощью вертикальных и горизонтальных линий связи.

Изометрическую проекцию цилиндра вычерчи­вают, как показано на рис. 166, б.

В изометрии точки A и В строят по координа­там. Например, для построения точки В от начала координат О по оси х откладывают координату x_B = n, а затем через ее конец проводят прямую, параллельную оси у, до пересечения с контуром основания в точке 1. Из этой точки параллельно оси x проводят прямую, на которой откладывают координату x_B = h₁ точки В.

Видео:Построение проекций пирамиды. Анимация.Скачать

Проекции конусов

Нагляднее изображение прямого кругового ко­нуса показано на рис. 167, а. Боковая поверхность конуса получена вращением отрезка BS вокруг оси, пересекающей отрезок в точке S. Последова­тельность построения двух проекций конуса пока­зана на рис. 167, б и в. Сначала строят две проекции основания. Горизонтальная проекция основа­ния — окружность. Фронтальной проекцией будет отрезок горизонтальной прямой, равный диаметру этой окружности (рис. 167, б). На фронтальной проекции из середины основания восставляют перпендикуляр и на нем откладывают высоту конуса (рис. 167, в). Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и по­лучают фронтальную проекцию конуса.

Если на поверхности конуса задана одна проек­ция точки А (например, фронтальная проекция на рис. 168, а). то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности ко­нуса и проведенной через точку А, или окружнос­ти, расположенной в плоскости, параллельной основанию конуса.

В первом случае (рис 168. а) проводят фрон­тальную проекцию s’a‘f ’ вспомогательной обра­зующей. Пользуясь вертикальной линией связи, проведенной из точки f, расположенной на фрон­тальной проекции окружности основания, находят горизонтальную проекцию sf этой образующей, на которой с помощью линии связи, проходящей через а’, находят искомую точку а.

Во втором случае (рис. 168. б) вспомогательной линией, проходящей через точку А, будет окруж­ность. расположенная на конической поверхности и параллельная плоскости Н. Фронтальная проек­ция этой окружности изображается в виде отрезка Ь’с’ горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция а точки А на­ходится на пересечении линии связи, опущенной из точки а’, с горизонтальной проекцией вспомо­гательной окружности.

Если заданная фронтальная проекция Ь’ точки В расположена на контурной (очерко­вой) образующей SK, то горизонтальная проекция точки находится без вспомогательных линий (рис. 168. б).

В изометрической проекции точку А, находя­щуюся на поверхности конуса, строят по трем координатам (рис. 168, в): x_А = n, y_А = m, z_А = h. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата x_А = n; из конца ее параллельно оси у проведена прямая, на которой отложена координата y_А = m; из конца отрезка, равного т, параллельно оси z проведена прямая, на которой отложена координата z_А = h. В резуль­тате построений получим искомую точку А.

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Проекции шара

На рис. 169, а изображена половина шара, сферическая поверхность этого шара образована вращением четверти окружности АВ вокруг ради­уса АО.

Проекции этой фигуры приведены на рис. 169, б. Горизонтальная проекция — окруж­ность радиуса, равного радиусу сферы, а фрон­тальная — полуокружность того же радиуса.

Если точка А расположена на сферической поверхности (рис. 169, в), то вспомогательная линия Ь’с’, проведенная через эту точку параллельно горизонтальной плоскости проекций, прое­цируется на горизонтальную плоскость проекций окружностью. На горизонтальной проекции вспо­могательной окружности находят с помощью ли­нии связи искомую горизонтальную проекцию а точки А.

Величина диаметра вспомогательной окружнос­ти равна фронтальной проекции Ь’с’.

Видео:Построение проекции пирамидыСкачать

Проекции кольца и тора

Поверхность кругового кольца (рис. 170, а) образована вращением образующей окружности ABCD вокруг оси ОО₁.

Тор — поверхность, образованная вращением части дуги окружности, являющейся образующей, вокруг оси ОО₁, расположенной в плоскости этой окружности и не проходящей через ее центр.

На рис. 171, а и б приведены два вида тора. В первом случае образующая дуга окружности радиуса R отстоит от оси вращения на расстоянии меньше радиуса R, а во втором случае — больше.

В обоих случаях фронтальные проекции тора представляют собой действительный вид двух образующих дуг окружности радиуса R, располо­женных симметрично относительно фронтальной проекции оси вращения. Профильными проекция­ми тора будут окружности.

Круговое кольцо (или открытый тор) имеет горизонтальную проекцию в виде двух концентри­ческих окружностей, разность радиусов которых равна толщине кольца или диаметру образующей окружности (рис. 170, б). Фронтальная проекция ограничивается справа и слева дугами полуокруж­ностей диаметра образующей окружности.

В случае, когда точка А лежит на поверхности кругового кольца и дана одна се проекция, для нахождения второй проекции этой точки приме­няется вспомогательная окружность, проходящая через данную точку А и расположенная на повер­хности кольца в плоскости, перпендикулярной оси кольца (рис. 172).

Если задана фронтальная проекция а’ точки А, лежащей на поверхности кольца, то для нахожде­ния ее второй проекции (в данном случае — про­фильной) через а’ проводят фронтальную проек­цию вспомогательной окружности — отрезок вер­тикальной прямой линии b‘c‘. Затем строят про­фильную проекцию b«с» этой окружности и на ней, применяя линию связи, находят точку а“.

Если задана профильная проекция а» точки D, расположенной на поверхности этого кольца, то для нахождения фронтальной проекции точки D через d« проводят профильную проекцию вспомо­гательной окружности радиуса O«d“. Затем через верхнюю и нижнюю точки е» f« этой окружности проводят горизонтальные линии связи до пересечения с фронтальными проекциями образующей окружности радиуса r и получают точки e‘ и f‘. Эти точки соединяют вертикальной прямой, кото­рая представляет собой фронтальную проекцию вспомогательной окружности (она будет невиди­ма). Проводя горизонтальную линию связи из точки d« до пересечения с прямой e‘f ‘, получаем искомую точку d‘.

Такие же приемы построения применимы и для точек, находящихся на поверхности тора.

Видео:ПОСТРОИТЬ ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА ПО ЗАДАННЫМ УСЛОВИЯМ. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.Скачать

Комплексные чертежи группы геометрических тел и моделей

Для развития пространственного воображения полезно выполнять комплексные чертежи группы геометрических тел и несложных моделей с натуры.

Наглядное изображение группы геометрических тел показано на рис. 173, а. Построение комплек­сного чертежа этой группы геометрических тел следует начинать с горизонтальной проекции, так как основания цилиндра, конуса и шестигранной пирамиды проецируются на горизонтальную плос­кость проекции без искажений. С помощью вертикальных линий связи строят фронтальную проек­цию. Профильную проекцию строят с помощью вертикальных и горизонтальных линий связи (рис. 173, б).

Чтобы перейти к более сложным моделям, не­обходимо усвоить построение простых комплек­сных чертежей. Проекции моделей следует распо­лагать таким образом, чтобы фронтальная проек­ция давала наиболее полное представление о фор­ме и размерах модели (рис. 174).

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

💥 Видео

Построить профильную и горизонтальную проекцию обрезанной ромбовидной призмы. Проекционное черчение.Скачать

Построение линии пересечения поверхности пирамиды с проецирующей плоскостьюСкачать

[Решение задач по начертательной геометрии] Построение проекции пирамидыСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Второй физический стрим!Скачать