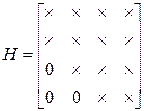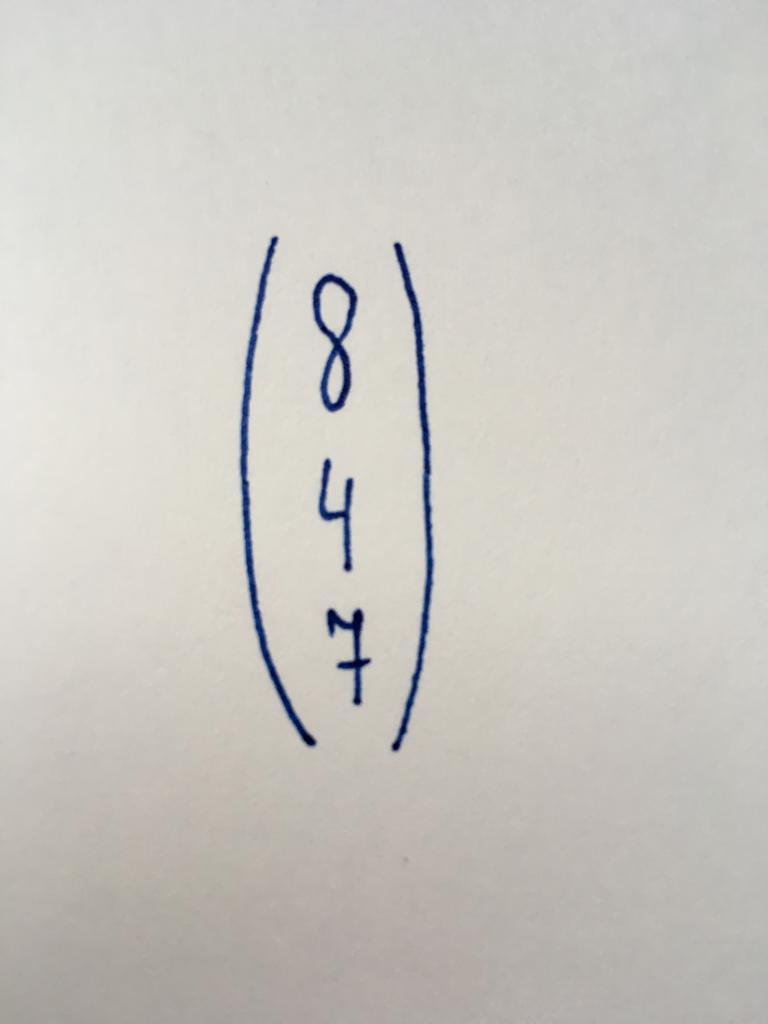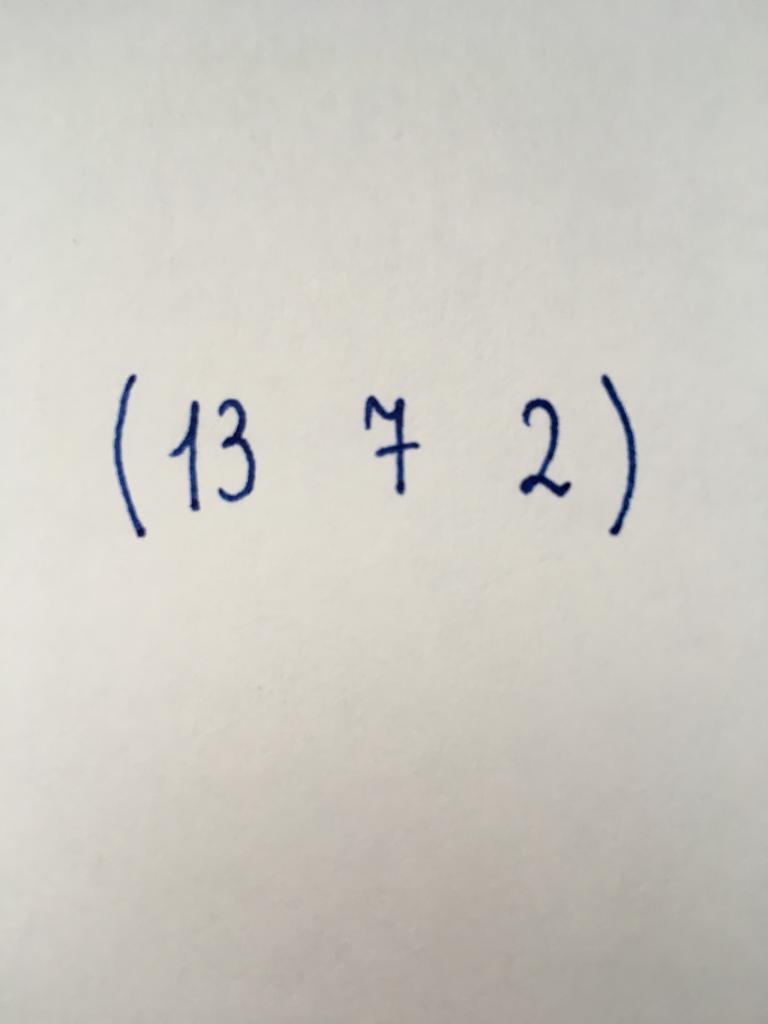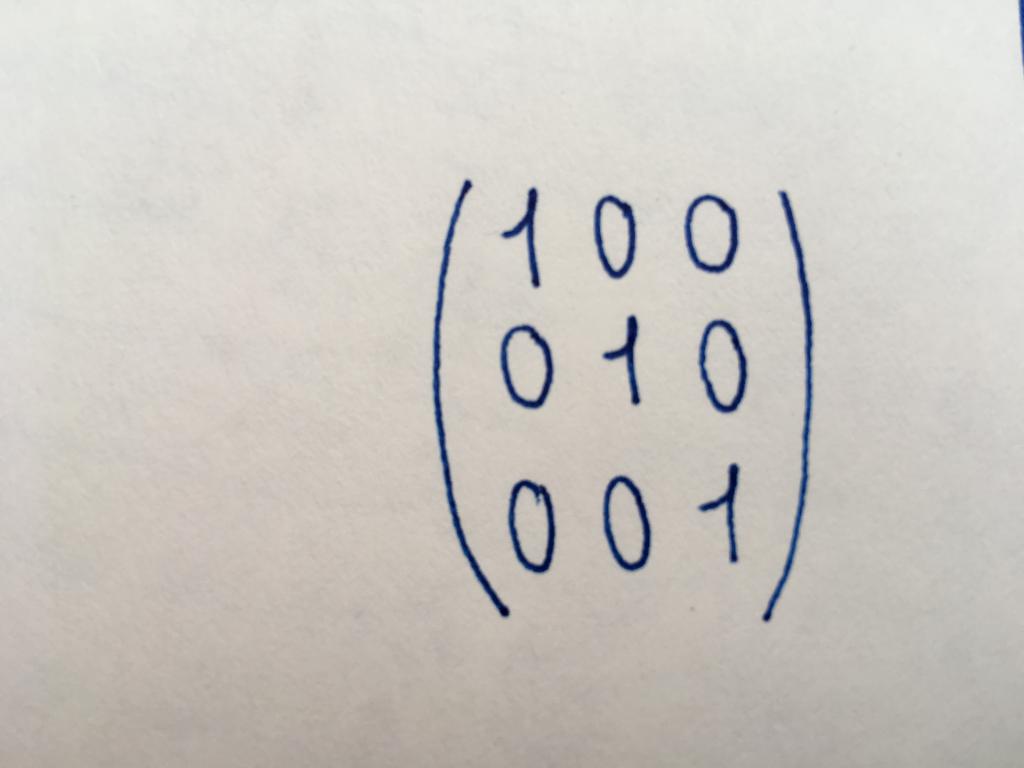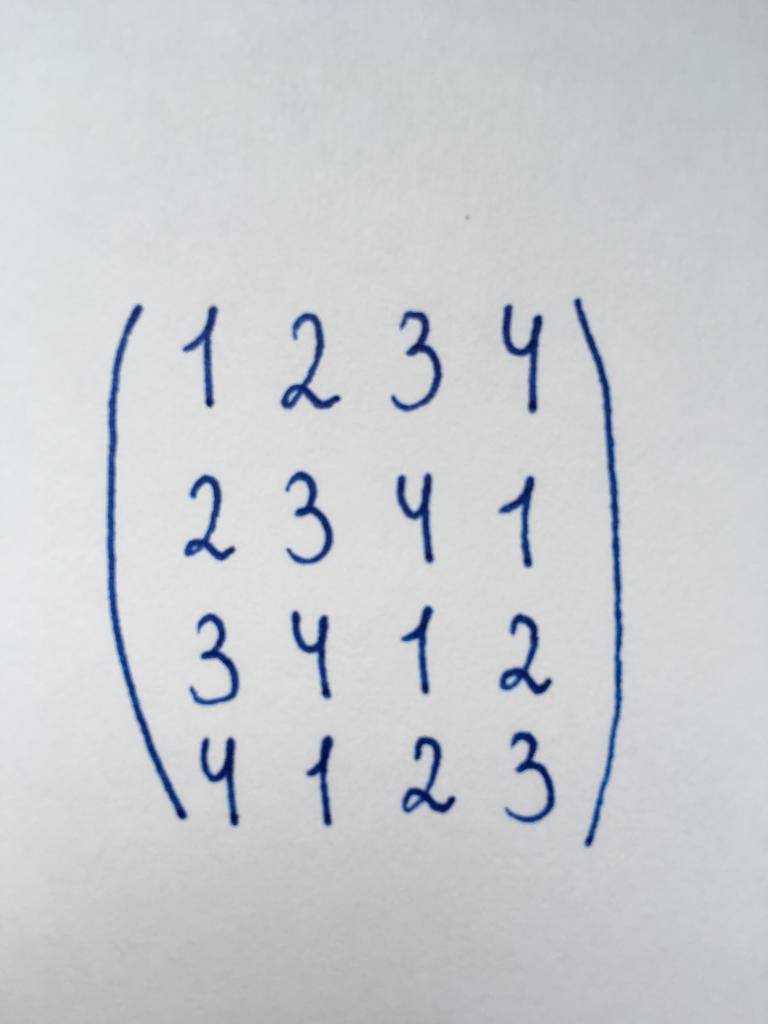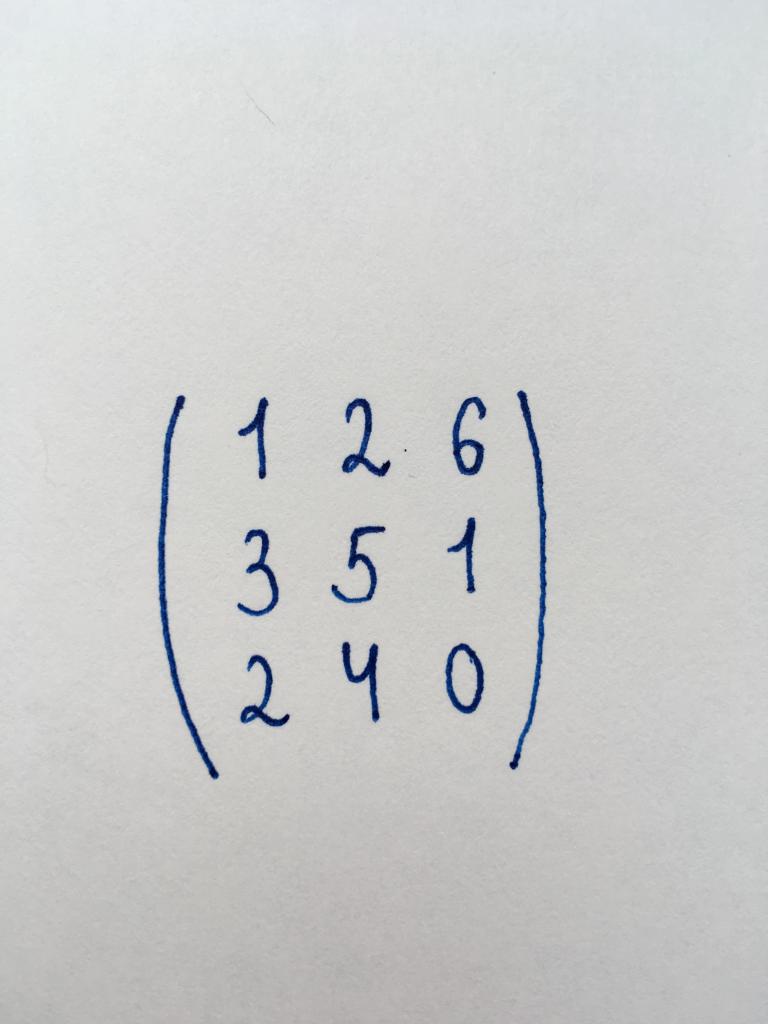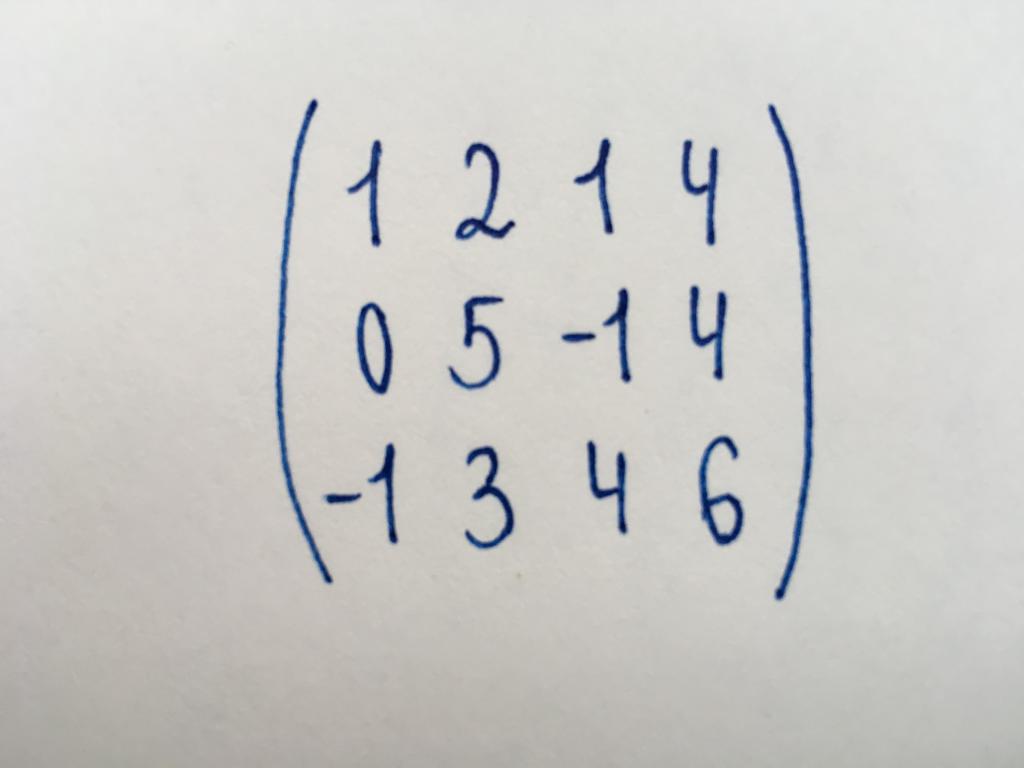Верхний треугольник вид матрицы

Квадратная матрица, у которой все элементы, расположенные ниже или выше главной диагонали, равны нулю, называется треугольной. Треугольная матрица может быть верхнего и нижнего строения. Верхняя и нижняя формы имеют соответственно вид:

, .

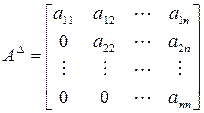
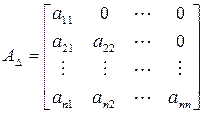
Треугольные матрицы обладают рядом важных в практическом отношении свойств:

1) Определитель треугольной матрицы равен произведению ее диагональных элементов:

.

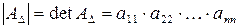
Следовательно, треугольная матрица является неособенной только тогда, когда все элементы ее главной диагонали отличны от нуля.

2) Сумма и произведение треугольных матриц одинакового строения есть также треугольная матрица того же строения.

3) Неособенная треугольная матрица легко обращается, и ее обратная матрица снова имеет треугольную структуру того же строения.

4) Всякая неособенная матрица при помощи элементарных преобразований только над строками или только над столбцами может быть приведена к треугольной матрице. В качестве примера рассмотрим известную в теории устойчивости матрицу Гурвица

.

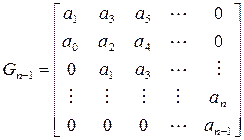
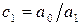
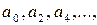
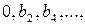
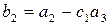
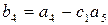
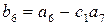
Для перехода к верхнему треугольному виду проделаем следующие элементарные преобразования. Из каждого элемента второй строки вычтем стоящий над ним элемент первой строки, предварительно умноженный на . Вместо строки с элементами получим строку с элементами где , , , . и т. д.

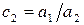
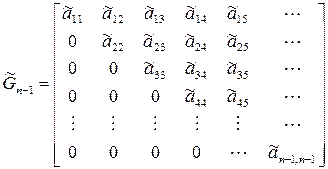
Выполним аналогичные операции в остальных нижележащих строках. Затем вычтем из каждого элемента третьей строки преобразованной матрицы стоящие над ней элементы строки, умноженные на , и повторим аналогичные операции в остальных строках. Продолжим процесс по этой процедуре до тех пор, пока на m-м шаге не получим верхнюю треугольную матрицу

.

Такие преобразования по существу эквивалентны умножению матрицы справа (или слева) на некоторую другую вспомогательную матрицу.

Определитель матрицы Гурвица

.

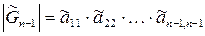
Существует теорема о разложении любой квадратной матрицы в произведение двух треугольных. Согласно этой теореме, всякая квадратная матрица может быть представлена в виде произведения нижней и верхней треугольных матриц:

,

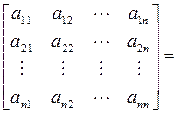
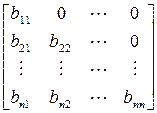
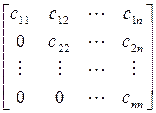
при условии, что ее диагональные миноры отличны от нуля:

, , .

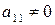
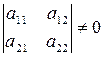
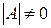
Это разложение является единственным, если зафиксировать диагональные элементы одной из треугольных матриц (например, положить их равными единице). Разложение любой квадратной матрицы в произведение двух треугольных с предписанными диагональными элементами широко используется в вычислительных методах при решении задач с помощью ЭВМ.

Однозначное представление матрицы в виде произведения двух треугольных может быть обобщено на клеточные матрицы. В таких матрицах сами элементы являются матрицами. При этом матрица может быть разложена в произведение нижней и верхней квазитреугольных матриц.

Определитель квазитреугольной матрицы равен произведению ее диагональных клеток.

В отличие от диагональных матриц операция умножения треугольных матриц в общем случае не коммутативна.

В вычислительных методах теории управления существенную роль играют не только треугольные, но и так называемые почти треугольные матрицы. Многие методы используют разложение матрицы в виде произведения двух матриц, одна из которых имеет треугольное строение. Матрица А называется правой (левой) почти треугольной или матрицей Хессенберга, если для ее элементов а_ij выполняются соотношения:

; ; .

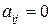
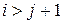
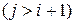
Например, матрица Хессенберга правой почти треугольной формы размерности (4×4) имеет вид

Отметим полезные особенности рассматриваемых матриц, которые используются в вычислительных методах:

а) сумма почти треугольных матриц одинакового строения будет треугольной матрицей того же строения, а произведение — нет;

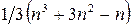
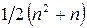
б) построение характеристического полинома почти треугольных матриц экономично, так как требует гораздо меньшего объема вычислений, чем при произвольной форме матрицы. Число операций умножений составляет , сложений — ;

в) почти треугольная матрица может быть разложена в произведение двух треугольных, причем в разложении одна из матриц будет иметь более простую структуру, а именно, будет двухдиагональной.

В современных инженерных методах, заложенных в системы автоматизированного проектирования, широко используется мультипликативное представление матриц, например, QR-представление. Его сущность состоит в том, что любую квадратную матрицу А можно представить в виде произведения ортогональной и почти треугольной форм

, или , (4.4)

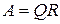
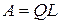
где Q — ортогональная матрица; R — правая (верхняя) треугольная форма; L — левая (нижняя) треугольная форма матрицы.

Представление (4.4) называется QR-разложением (в случае нижней треугольной матрицы QL-разложением) и для матрицы А является единственным.

QR- и QL-алгоритмы принципиально мало различаются. Их использование зависит от того, как расположены элементы матрицы. Если они сосредоточены в нижнем правом углу, эффективнее использовать QL-алгоритм. Если элементы матрицы сосредоточены в левой верхней части, то целесообразнее использовать QR-алгоритм. При правильной реализации на ЭВМ ошибки округления во многих случаях не оказывают большого влияния на точность вычисления.

Дата добавления: 2014-12-27 ; просмотров: 6304 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:5 способов вычисления определителя ★ Какой способ лучше?Скачать

Виды матриц. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому и треугольному виду

Матрица — это особый объект в математике. Изображается в форме прямоугольной или квадратной таблицы, сложенной из определенного числа строк и столбцов. В математике имеется большое разнообразие видов матриц, различающихся по размерам или содержанию. Числа ее строк и столбцов именуются порядками. Эти объекты употребляются в математике для упорядочивания записи систем линейных уравнений и удобного поиска их результатов. Уравнения с использованием матрицы решаются посредством метода Карла Гаусса, Габриэля Крамера, миноров и алгебраических дополнений, а также многими другими способами. Базовым умением при работе с матрицами является приведение к стандартному виду. Однако для начала давайте разберемся, какие виды матриц выделяют математики.

Видео:Приведение определителя к треугольному видуСкачать

Нулевой тип

Все компоненты этого вида матрицы — нули. Между тем, число ее строк и столбцов абсолютно различно.

Видео:Как привести матрицу к ступенчатому виду - bezbotvyСкачать

Квадратный тип

Количество столбцов и строк этого вида матрицы совпадает. Иначе говоря, она представляет собой таблицу формы «квадрат». Число ее столбцов (или строк) именуются порядком. Частными случаями считается существование матрицы второго порядка (матрица 2×2), четвертого порядка (4×4), десятого (10×10), семнадцатого (17×17) и так далее.

Видео:Определитель матрицы 3 порядка. Как легко найти? Метод треугольников и Саррюса. Просто и наглядноСкачать

Вектор-стобец

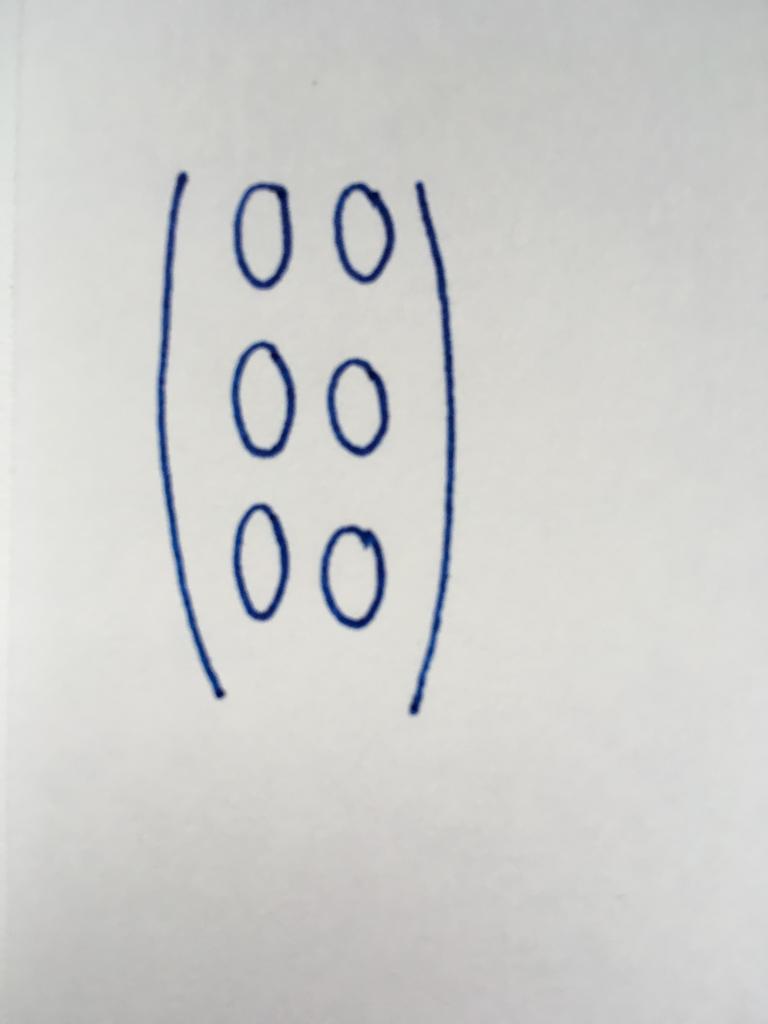
Это один из простейших видов матриц, содержащий только один столбец, который включает в себя три численных значения. Она представляет ряд свободных членов (чисел, независимых от переменных) в системах линейных уравнений.

Видео:§16 Приведение определителей к треугольному видуСкачать

Вектор-строка

Вид, аналогичный предыдущему. Состоит из трех численных элементов, в свою очередь организованных в одну строку.

Видео:Определитель 5 порядка приводим к треугольному видуСкачать

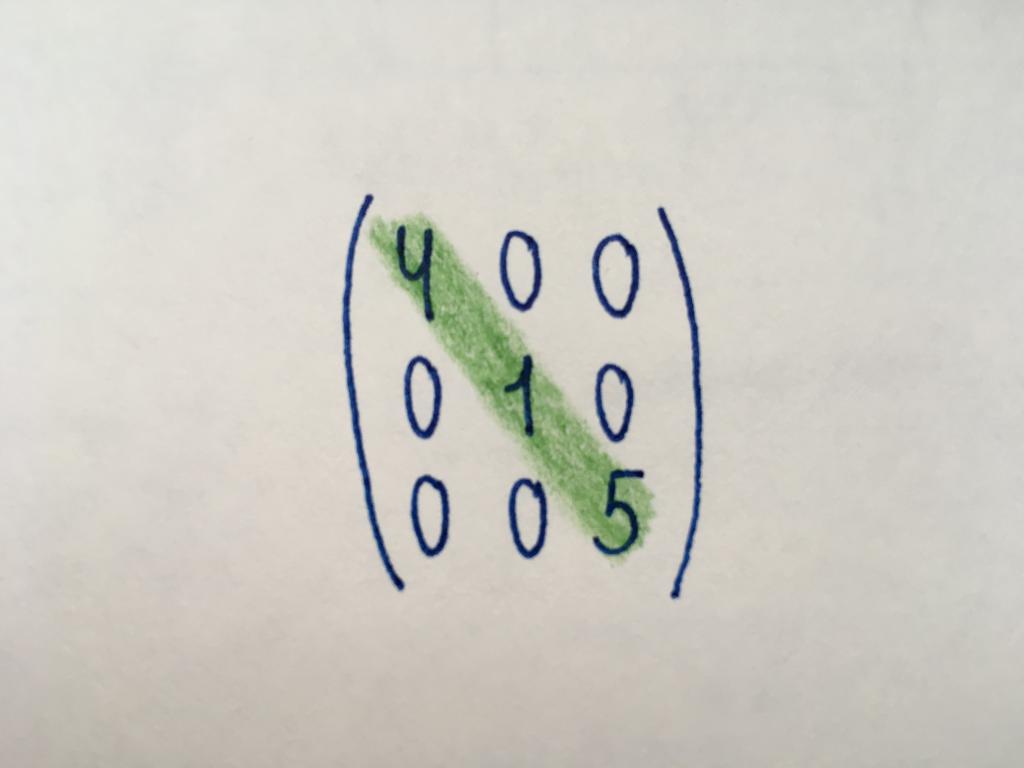
Диагональный тип

Числовые значения в диагональном виде матрицы принимают только компоненты главной диагонали (выделена зеленым цветом). Основная диагональ начинается с элемента, находящегося в левом верхнем углу, а заканчивается элементом в правом нижнем соответственно. Остальные компоненты равны нулю. Диагональный тип представляет собой только квадратную матрицу какого-либо порядка. Среди матриц диагонального вида можно выделить скалярную. Все ее компоненты принимают одинаковые значения.

Видео:Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать

Единичная матрица

Подвид диагональной матрицы. Все ее числовые значения являются единицами. Используя единичный тип матричных таблиц, выполняют ее базовые преобразования или находят матрицу, обратную исходной.

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

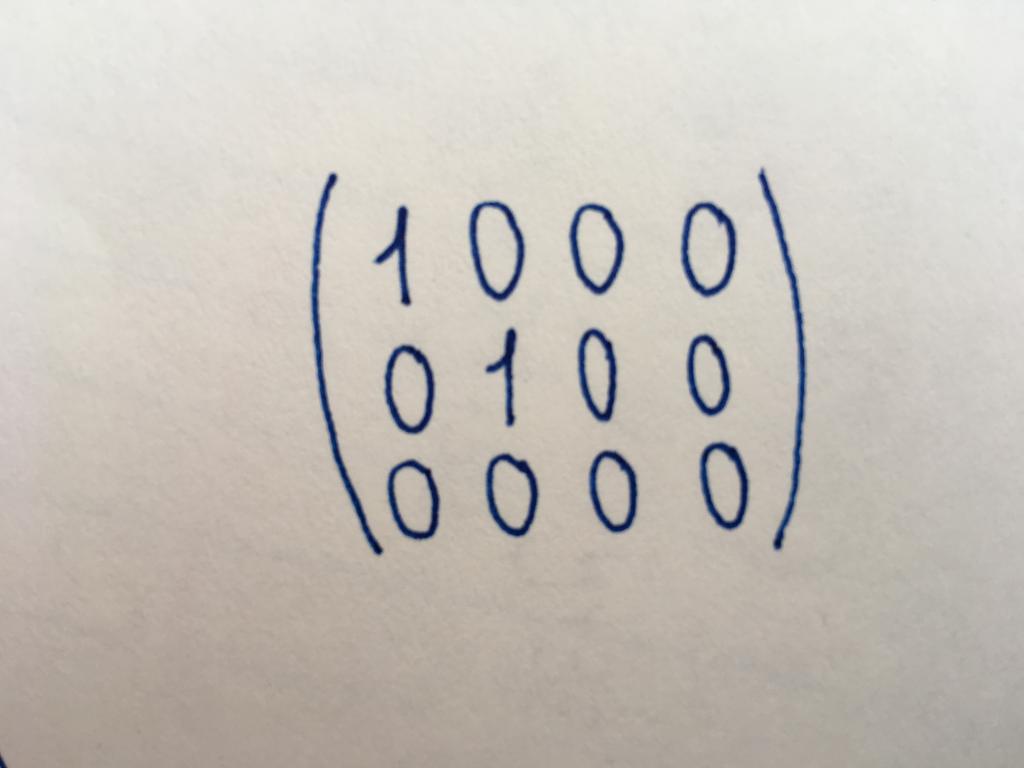
Канонический тип

Канонический вид матрицы считается одним из основных; приведение к нему часто необходимо для работы. Число строк и столбцов в канонической матрице различно, она необязательно принадлежит к квадратному типу. Она несколько похожа на единичную матрицу, однако в ее случае не все компоненты основной диагонали принимают значение, равное единице. Главнодиагональных единиц может быть две, четыре (все зависит от длины и ширины матрицы). Или единицы могут не иметься вовсе (тогда она считается нулевой). Остальные компоненты канонического типа, как и элементы диагонального и единичного, равны нулю.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Треугольный тип

Один из важнейших видов матрицы, применяемый при поиске ее детерминанта и при выполнении простейших операций. Треугольный тип происходит от диагонального, поэтому матрица также является квадратной. Треугольный вид матрицы подразделяют на верхнетреугольный и нижнетреугольный.

В верхнетреугольной матрице (рис. 1) только элементы, которые находятся над главной диагональю, принимают значение, равное нулю. Компоненты же самой диагонали и части матрицы, располагающейся под ней, содержат числовые значения.

В нижнетреугольной (рис. 2), наоборот, элементы, располагающиеся в нижней части матрицы, равны нулю.

Видео:Обратная матрицаСкачать

Ступенчатая матрица

Вид необходим для нахождения ранга матрицы, а также для элементарных действий над ними (наряду с треугольным типом). Ступенчатая матрица названа так, потому что в ней содержатся характерные «ступени» из нулей (как показано на рисунке). В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю. Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.

Таким образом, мы рассмотрели важнейшие типы матриц, необходимые для работы с ними. Теперь разберемся с задачей преобразования матрицы в требуемую форму.

Видео:Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Приведение к треугольному виду

Как же привести матрицу к треугольному виду? Чаще всего в заданиях нужно преобразовать матрицу в треугольный вид, чтобы найти ее детерминант, по-другому называемый определителем. Выполняя данную процедуру, крайне важно «сохранить» главную диагональ матрицы, потому что детерминант треугольной матрицы равен именно произведению компонентов ее главной диагонали. Напомню также альтернативные методы нахождения определителя. Детерминант квадратного типа находится при помощи специальных формул. Например, можно воспользоваться методом треугольника. Для других матриц используют метод разложения по строке, столбцу или их элементам. Также можно применять метод миноров и алгебраических дополнений матрицы.

Подробно разберем процесс приведения матрицы к треугольному виду на примерах некоторых заданий.

Видео:Вычислить определитель 3 порядка. Правило треугольникаСкачать

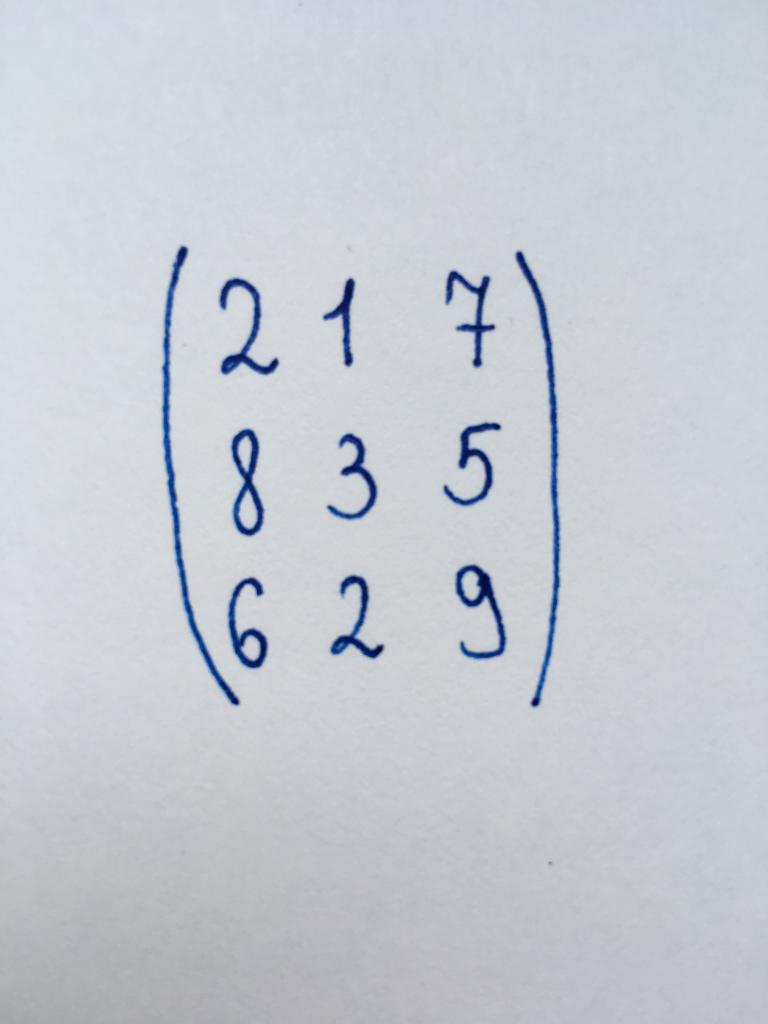
Задание 1

Необходимо найти детерминант представленной матрицы, используя метод приведения его к треугольному виду.

Данная нам матрица представляет собой квадратную матрицу третьего порядка. Следовательно, для ее преобразования в треугольную форму нам понадобится обратить в нуль два компонента первого столбца и один компонент второго.

Чтобы привести ее к треугольному виду, начнем преобразование с левого нижнего угла матрицы — с числа 6. Чтобы обратить его в нуль, умножим первую строку на три и вычтем ее из последней строки.

Важно! Верхняя строка не изменяется, а остается такой же, как и в исходной матрице. Записывать строку, в четыре раза большую исходной, не нужно. Но значения строк, компоненты которых нужно обратить в нуль, постоянно меняются.

Далее займемся следующим значением — элементом второй строки первого столбца, числом 8. Умножим первую строку на четыре и вычтем ее из второй строки. Получим нуль.

Осталось только последнее значение — элемент третьей строки второго столбца. Это число (-1). Чтобы обратить его в нуль, из первой строки вычтем вторую.

detA = 2 x (-1) x 11 = -22.

Значит, ответ к заданию: -22.

Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

Задание 2

Нужно найти детерминант матрицы методом приведения его к треугольному виду.

Представленная матрица принадлежит к квадратному типу и является матрицей четвертого порядка. Значит, необходимо обратить в нуль три компонента первого столбца, два компонента второго столбца и один компонент третьего.

Начнем приведение ее с элемента, находящегося в нижнем углу слева, — с числа 4. Нам нужно обратить данное число в нуль. Удобнее всего сделать это, умножив на четыре верхнюю строку, а затем вычесть ее из четвертой. Запишем итог первого этапа преобразования.

Итак, компонент четвертой строки обращен в нуль. Перейдем к первому элементу третьей строки, к числу 3. Выполняем аналогичную операцию. Умножаем на три первую строку, вычитаем ее из третьей строки и записываем результат.

Далее видим число 2 во второй строке. Повторяем операцию: умножаем верхнюю строку на два и вычитаем ее из второй.

Нам удалось обратить в нуль все компоненты первого столбца данной квадратной матрицы, за исключением числа 1 — элемента главной диагонали, не требующего преобразования. Теперь важно сохранить полученные нули, поэтому будем выполнять преобразования со строками, а не со столбцами. Перейдем ко второму столбцу представленной матрицы.

Снова начнем с нижней части — с элемента второго столбца последней строки. Это число (-7). Однако в данном случае удобнее начать с числа (-1) — элемента второго столбца третьей строки. Чтобы обратить его в нуль, вычтем из третьей строки вторую. Затем умножим вторую строку на семь и вычтем ее из четвертой. Мы получили нуль вместо элемента, расположенного в четвертой строке второго столбца. Теперь перейдем к третьему столбцу.

В данном столбце нам нужно обратить в нуль только одно число — 4. Сделать это несложно: просто прибавляем к последней строке третью и видим необходимый нам нуль.

После всех произведенных преобразований мы привели предложенную матрицу к треугольному виду. Теперь, чтобы найти ее детерминант, нужно только произвести умножение получившихся элементов главной диагонали. Получаем: detA = 1 x (-1) x (-4) x 40 = 160. Следовательно, решением является число 160.

Итак, теперь вопрос приведения матрицы к треугольному виду вас не затруднит.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Приведение к ступенчатому виду

При элементарных операциях над матрицами ступенчатый вид является менее «востребованным», чем треугольный. Чаще всего он используется для нахождения ранга матрицы (т. е. количества ее ненулевых строк) или для определения линейно зависимых и независимых строк. Однако ступенчатый вид матрицы является более универсальным, так как подходит не только для квадратного типа, но и для всех остальных.

Чтобы привести матрицу к ступенчатому виду, сначала нужно найти ее детерминант. Для этого подойдут вышеназванные методы. Цель нахождения детерминанта такова: выяснить, можно ли преобразовать ее в ступенчатый вид матрицы. Если детерминант больше или меньше нуля, то можно спокойно приступать к заданию. Если же он равен нулю, выполнить приведение матрицы к ступенчатому виду не получится. В таком случае нужно проверить, нет ли ошибок в записи или в преобразованиях матрицы. Если подобных неточностей нет, задание решить невозможно.

Рассмотрим, как привести матрицу к ступенчатому виду на примерах нескольких заданий.

Задание 1. Найти ранг данной матричной таблицы.

Перед нами квадратная матрица третьего порядка (3×3). Мы знаем, что для нахождения ранга необходимо привести ее к ступенчатому виду. Поэтому сначала нам необходимо найти детерминант матрицы. Воспользуемся методом треугольника: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) — (1 x 1 x 4) — (2 x 3 x 0) — (6 x 5 x 2) = 12.

Детерминант = 12. Он больше нуля, значит, матрицу можно привести к ступенчатому виду. Приступим к ее преобразованиям.

Начнем его с элемента левого столбца третьей строки — числа 2. Умножаем верхнюю строку на два и вычитаем ее из третьей. Благодаря этой операции как нужный нам элемент, так и число 4 — элемент второго столбца третьей строки — обратились в нуль.

Далее обращаем в нуль элемент второй строки первого столбца — число 3. Для этого умножаем верхнюю строку на три и вычитаем ее из второй.

Мы видим, что в результате приведения образовалась треугольная матрица. В нашем случае продолжить преобразование нельзя, так как остальные компоненты не удастся обратить в нуль.

Значит, делаем вывод, что количество строк, содержащих числовые значения, в данной матрице (или ее ранг) — 3. Ответ к заданию: 3.

Задание 2. Определить количество линейно независимых строк данной матрицы.

Нам требуется найти такие строки, которые нельзя какими-либо преобразованиями обратить в нуль. Фактически нам нужно найти количество ненулевых строк, или ранг представленной матрицы. Для этого выполним ее упрощение.

Мы видим матрицу, не принадлежащую к квадратному типу. Она имеет размеры 3×4. Начнем приведение также с элемента левого нижнего угла — числа (-1).

Прибавляем первую строку к третьей. Далее вычитаем из нее вторую, чтобы обратить число 5 в нуль.

Дальнейшие ее преобразования невозможны. Значит, делаем вывод, что количество линейно независимых строк в ней и ответ к заданию — 3.

Теперь приведение матрицы к ступенчатому виду не является для вас невыполнимым заданием.

На примерах данных заданий мы разобрали приведение матрицы к треугольному виду и ступенчатому виду. Чтобы обратить в нуль нужные значения матричных таблиц, в отдельных случаях требуется проявить фантазию и правильно преобразовать их столбцы или строки. Успехов вам в математике и в работе с матрицами!

Видео:6. Вычисление определителя 2 и 3 порядка.Скачать

Приведение матрицы к виду верхней треугольной «Алгоритм Барейса»

Матрица — двумерный массив. Это особый тип организации данных, который выступает как единое и неразрывное целое.

1. Актуальность Алгоритма Барейса
2. Матрицы треугольного вида
3. Суть Алгоритма Барейса
4. Исходный код VBA EXCEL

Данные в матрице строго структурированы и несут (сохраняют) причинно следственные связи.

Видео:8 Гц, 64 Гц, 128 Гц Треугольник Святого Духа Исцеляющий Сеанс по ЛевашовуСкачать

Актуальность Алгоритма Барейса

Как и вся матричная арифметика, алгоритм Барейса совершенствует (упрощает) способ обработки данных, находящихся в матрице.

Приведение матрицы к треугольному виду требуется, прежде всего, для решения систем линейных уравнений, а именно для вычисления определителя матрицы. Ведь самый быстрый способ вычислить определитель — это привести матрицу к треугольному виду (по алгоритму Гаусса), а затем перемножить её диагональные элементы.
О дополнительных преимуществах алгоритма Барейса сказано ниже…

Видео:МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицамиСкачать

Матрицы треугольного вида

Название говорит само за себя.

Если все элементы матрицы ниже главной диагонали равны 0, то это верхняя треугольная матрица. Если выше главной диагонали все 0, то это нижняя треугольная матрица.

Видео:Ранг матрицыСкачать

Суть Алгоритма Барейса

Изучив преимущества и недостатки имеющихся алгоритмов (Гаусса и Барейса), я остановился на алгоритме Барейса, так как:

• если матрица состоит из целых чисел, алгоритм Барейса позволяет привести её к треугольному виду с использованием только целочисленной арифметики;
• определитель исходной матрицы равен правому нижнему элементу матрицы, полученной в результате алгоритма Барейса, т.е. не нужно выполнять перемножение элементов главной диагонали, как после алгоритма Гаусса;
• алгоритм Барейса так же, как и алгоритм Гаусса, может быть улучшен путём добавления перестановки строк, но в нашей задаче это излишне;

Поэтому код VBA приведения будет следующим:
For j = 1 To n — 1
jj = mR.Cells(j, j) ‘определяем первый множитель

If j = 1 Then ‘определяем знаменатель
znm = 1
Else
znm = mR.Cells(j — 1, j — 1)
If znm = 0 Then Exit Function
End If

For i = j + 1 To n
ij = mR.Cells(i, j) ‘определяем второй множитель

For k = j To n
mR.Cells(i, k) = (jj * mR.Cells(i, k) — ij * mR.Cells(j, k)) / znm
Next k

Где mR as Range – переменная модуля, ссылающаяся на выделенная область.

j— индексы строк, а i— индексы столбцов выделенной области.
Ячейка, обозначенная как а_-1,-1 лежит вне области выделения (т.е. выше и левее ячейки а_0,0 ) и ей в начальный период обязательно присваивается 1. В своей функции вместо а_-1,-1 я использую переменную znm (от знаменатель) и базовое значение счетчиков 1 вместо 0. Суть алгоритма это не меняет. При пошаговом выполнении программы прекрасно прослеживается постепенное приведение матрицы к верхнему треугольному виду.

Видео:Как найти ранг матрицы (пример) - bezbotvyСкачать

Исходный код VBA EXCEL

Для работы с матрицами в Microsoft EXCEL существует три функции листа Excel.
Это:

1. МОПРЕД(массив) — возвращает определитель матрицы (матрица хранится в массиве);
2. МОБР(массив) — возвращает обратную матрицу для матрицы, хранящейся в массиве;
3. МУМНОЖ(массив1;массив2) — возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2;

Первую из этих функций буду использовать для проверки результата.

Кроме того:

• в макросе проводится проверка на соответствие выделенной области, и если размеры не совпадают (а матрица должна быть квадратной), то выдается сообщение и работа макроса завершается;
• в ячейку AJ2 вводится формула для вычисления определителя (на основе функции МОПРЕД) выделенной области; (просто для проверки)
• в завершающем сообщении предлагается очистить лист «Результат» по желанию пользователя;

Если у Вас остались вопросы, то задать их Вы можете, нажав на эту кнопочку .

🔥 Видео

Как вычислить определитель матрицы четвертого порядка | Высшая математикаСкачать