Знание — сила. Познавательная информация
- Рисунок правильной пирамиды
- Как лучше нарисовать пирамиду
- Правило метода изображений.
- Читабельность рисунка.
- Фронтальное изображение тетраэдра. Правило репетитора.
- Правильная треугольная пирамида
- В основании пирамиды правильный треугольник (все стороны которого равны, углы между сторонами основания составляют 60 градусов).
- Популярное
- 🎥 Видео
Видео:оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How to make Paper PyramidСкачать

Рисунок правильной пирамиды
Чертеж — первый и очень важный шаг в решении геометрической задачи. Каким должен быть рисунок правильной пирамиды?
Сначала вспомним свойства параллельного проектирования:
— параллельные отрезки фигуры изображаются параллельными отрезками;
— сохраняется отношение длин отрезков параллельных прямых и отрезков одной прямой.
Рисунок правильной треугольной пирамиды
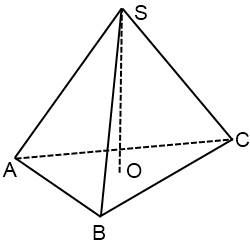
Центр правильного треугольника — точка пересечения медиан треугольника. Поскольку медианы в точке пересечения делятся в отношении 2:1, считая от вершины, мысленно соединяем вершину основания с серединой противолежащей стороны, приблизительно делим ее на три части, и на расстоянии 2 частей от вершины ставим точку. Из этой точки вверх проводим перпендикуляр. Это — высота пирамиды. Перпендикуляр рисуем такой длины, чтобы боковое ребро не закрывало изображение высоты.
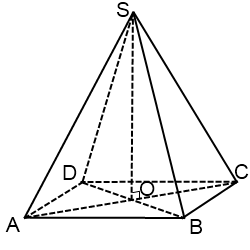
Рисунок правильной четырехугольной пирамиды
Рисунок правильной четырехугольной пирамиды также начинаем с основания. Поскольку параллельность отрезков сохраняется, а величины углов — нет, то квадрат в основании изображается параллелограммом. Желательно острый угол этого параллелограмма делать поменьше, тогда боковые грани получаются больше. Центр квадрата — точка пересечения его диагоналей. Проводим диагонали, из точки пересечения восстанавливаем перпендикуляр. Этот перпендикуляр — высота пирамиды. Выбираем длину перпендикуляра таким образом, чтобы боковые ребра не сливались между собой.
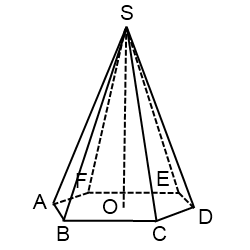
Рисунок правильной шестиугольной пирамиды
Поскольку при параллельном проектировании параллельность отрезков сохраняется, основание правильной шестиугольной пирамиды — правильный шестиугольник — изображаем шестиугольником, у которого противолежащие стороны параллельны и равны. Центр правильного шестиугольника — точка пересечения его диагоналей. Чтобы не загромождать рисунок, диагонали не проводим, а находим эту точку приблизительно. Из нее восстанавливаем перпендикуляр — высоту пирамиды — так, чтобы боковые ребра не сливались между собой.
Видео:Как начертить правильную треугольную пирамиду на #ЕГЭ2023 #стереометрияСкачать

Как лучше нарисовать пирамиду
by Колпаков А.Н. on 8 июля 2011
К азалось бы, что может быть сложного или неправильного в изображении пирамиды? Неужели и здесь репетитор по математике не обходится без специальных приемов и методик? Отмечается всего лишь 4 точки (любые 3 из которых не лежат на одной прямой) и соединяются шестью отрезками. И все. Что здесь обсуждать? Но даже в такой простой ситуации репетитору по математике приходится исправлять ученические ошиби. Даже не столько математические, сколько стратегические. Какие? Рисунок, на котором невозможно рассмотреть или показать элементы пространственного тела, подписать значения величин, на котором не развернуться с дополнительными построениями, лучше переделать. Это должен понимать любой репетитор и в начале курса подготовки к ЕГЭ потратить некоторое время на обучение правилам и культуре чертежа. Кроме требований к его аккуратности и удобному расположению информации из условия задачи существуют еще и математические законы его выполнения. Рассмотрим их подробнее.
Правило метода изображений.
Метод изображений — отдельный предмет, изучению которого на математическом факультете МПГУ отводится целый семестр. То, что мы рисуем на бумаге – следы от проекций частей тела на некоторую плоскость. От нее зависит то, какие отрезки и какие сечения будут отчетливо видны, а какие окажутся «наползающими» друг на друга или скрытыми. Когда репетитор по математике решает, с какой стороны нарисовать ученику пирамиду, он определяет расположение плоскости и направление проецирования.
Существуют геометрические законы проецирования простейших стереометрических объектов. Длины непараллельных отрезков, например, при изображении могут менять соотношение своих длин (преподавателю лучше произнести «искажаются»). Если в реальности один из них больше другого, то в проекции может быть все с точностью до наоборот. Тоже самое и с углами. Прямой угол может проецироваться как в острый, так и в тупой. Для того, чтобы репетитору математики убедить в этом ученика стоит покрутить перед его глазами обычный угольник. Однако отношение длин отрезков, лежащих на параллельных или совпадающих прямых, не меняется и, в частности, не искажаются середины сторон многоугольников (граней пирамиды). Это объясняет закон расположения основания высоты правильной треугольной пирамиды: оно должно являться точкой пересечения его медиан (центром тяжести). Не искажается также параллельность. Если в пространстве имеется параллельность между прямыми, то она сохраняется и между их следами. Поэтому изображением основания правильной четырехугольной пирамиды выбирается параллелограмм.
Читабельность рисунка.
Важно расположить пирамиду так, чтобы все ее части не просто были видны, а допускали бы дальнейшее усложнение чертежа: проведение апофем, следов от сечений и т.д.
Для этого строить, например, правильную пирамиду желательно снизу вверх через высоту (так она используется почти во всех задачах). Сначала репетитор по математике рисует основание пирамиды, затем ее центр и из этой точки восстанавливает перпендикуляр. 
Построение основания.
Независимо от вида основания тетраэдра его изображают остроугольным треугольником и вытягивают влево или вправо. Зачем? Если он будет равнобедренным, то одно из боковых ребер закроет высоту (если конечно ее основание правильно расположено). Это показано на рисунке.
Фронтальное изображение тетраэдра. Правило репетитора.
Каким краем лучше всего изобразить пирамиду? То есть как оптимально выбрать плоскость для проецирования? Некоторые преподаватели и репетиторы по математике, к сожалению, не обращают внимание на такую «мелочь» как фронтальное расположение пирамиды. А зря. Существует два вида рисунка: «уголком основания к нам» или «уголком от нас» Рассмотрим рисунок с «уголком ABC от нас»:
Восстанавливаем высоту снизу вверх и выбираем положение ее конца (вершины пирамиды) с расчетом на приемлемый размах грани ABP. Для этого самое главное не попасть точкой P на линию AB. Иначе мы грань не увидим. Значительное отклонение от точки пересечения (в изображении) линий AB и OP вызывает довольно небольшое отклонение луча AP от луча AB и поэтому, чтобы добиться размаха грани ABP, необходимо выбирать точку P или очень низко или очень высоко. 



Прорисовка невидимых линий.
Репетитор по математике, конечно, может обойтись и без пунктиров. Однако что русскому то хорошо, то немцу смерь. Ученику — важно воспринять тело именно с той стороны, с которой его видит репетитор. Особенно при работе с гранями. Я советую преподавателю математики чаще называть грани не по вершинам, а по их естественному расположению: «ближняя», «дальняя», «левая», «правая». Если в голове у ребенка сформируется образ объекта «задом наперед», то возникнут проблемы с описанием хода дополнительных построений, чтением рисунка и даже с объяснением непонятных моментов решений.
о построении четырехугольной пирамиды.
Основание правильной четырехугольной пирамиды следует изображаться в виде параллелограмма. Почему? Конечно, можно так расположить квадрат к плоскости проецирования, чтобы прямые углы сохранились (и мы получим прямоугольник), но тогда апофемы двух ближних граней будут закрывать высоту пирамиды. Другого объяснения сложившимся стандартам изображений я не нахожу.
Александр Колпаков, репетитор по математике в Москве. Подготовка к ЕГЭ.
Сайт вызывает восхищение уровнем профессионализма, прежде всего, в методическом плане. Нашел много поучительного для себя, имея опыт репетиторства с 70-х годов прошлого века (по физике).
Сейчас развивается онлайн репетиторство и там непочатый край работы для мастеров класса Александра Николаевича.
Я,ученик 11 класса,рад что прочитал эту страничку,потому что до этого я рисовал чертежи как попало.Теперь,под конец года, я понял многие вещи о построении фигур.
Видео:Как нарисовать пирамиду?Скачать
Правильная треугольная пирамида
Видео:Как начертить ПИРАМИДУ в объемеСкачать
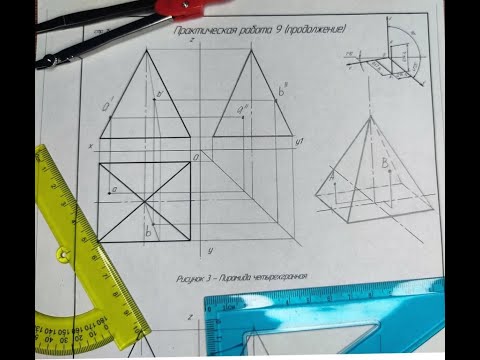
В основании пирамиды правильный треугольник (все стороны которого равны, углы между сторонами основания составляют 60 градусов).
Популярное
В естественной среде правильные многогранники можно встретить в виде кристаллов (минералов). Форму тетраэдра передает сурьмянистый сернокислый натрий.
Сделать новогодний праздник красивым и необычным, чтобы дети видели в нём сказку, а гости восхищались, можно только своими руками. Бумажные многогранники –.
Одинаковым узором, повторяющимся на каждой грани многогранника, можно создать чередующуюся комбинацию рисунков на объемном геометрическом теле.
Бывают совпадения, о которых мы даже сами не подозреваем. 12 апреля — День Космонавтики!
Существует концепция, что вершина многогранника отдает энергию, а плоскость энергию принимает. В том случае, если в многограннике вершин больше чем плоскостей, то он обладает.
Совершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира.
Он круглый, но развёртку деталей для его сборки никто не отменял!
🎥 Видео
Треугольная пирамида. Проекции точек на гранях. Сечение. Урок23.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Построение проекции пирамиды. Метод прямого треугольника.Скачать

УРОК 3.КАК НАРИСОВАТЬ ПРИЗМУ,ПИРАМИДУ.Обучение рисунку.Урок рисования карандашом.построение поэтапноСкачать

Как рисовать правильный шестиугольник в основанииСкачать
Треугольная пирамида. Ортогональные и изометрическая проекции.Урок22.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

«КАК РИСОВАТЬ ШЕСТИГРАННУЮ ПИРАМИДУ?» Цикл уроков от Дениса Чернова | Урок №2 | AkademikaСкачать

Пирамида из бумаги/Paper pyramid/DIYСкачать

3D Пирамида-Треугольник Объемный рисунок по Клеточкам #pixelvideoСкачать

Как строить сечения тетраэдра и пирамидыСкачать

Развертка треугольной равносторонней пирамиды. Урок24.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Развертка пирамидыСкачать

Развертка тетраэдра - это легко! Как сделать объёмную правильную треугольную пирамиду из бумаги?Скачать

КАК НАРИСОВАТЬ ТРЕУГОЛЬНИК В КОНСОЛИ C# | C# ДОМАШНИЕ ЗАДАНИЯ | #5Скачать

ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Построить модель ПИРАМИДЫ в КОМПАС-3DСкачать

Как начертить ПРИЗМУ ТРЕХГРАННУЮСкачать