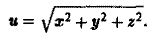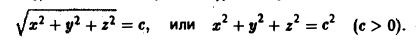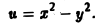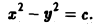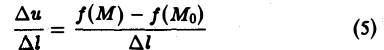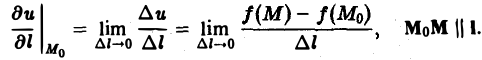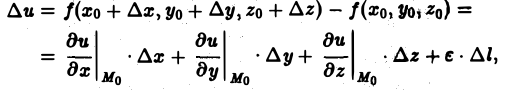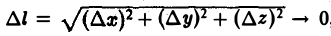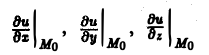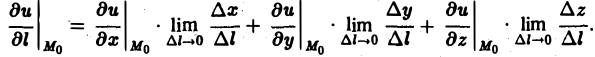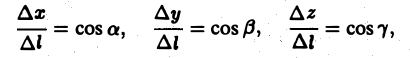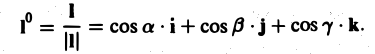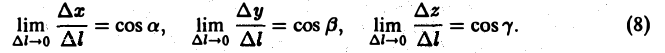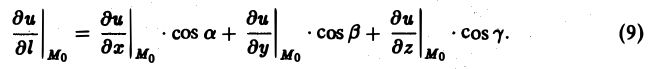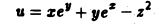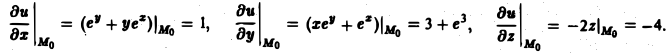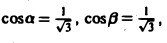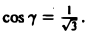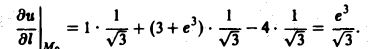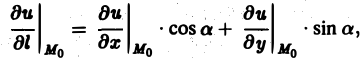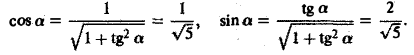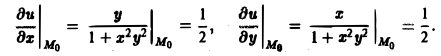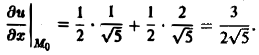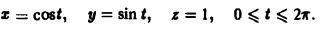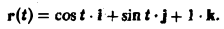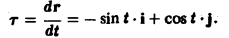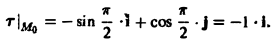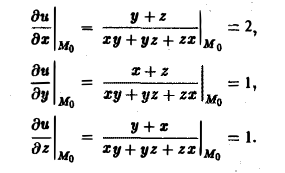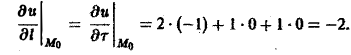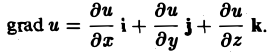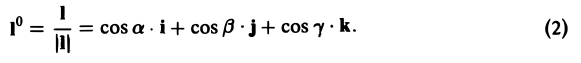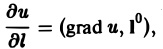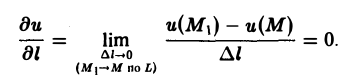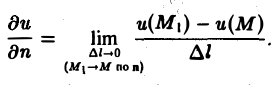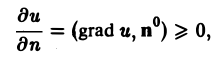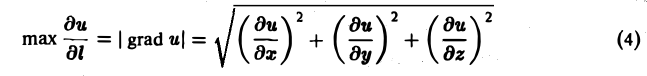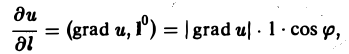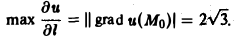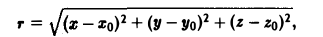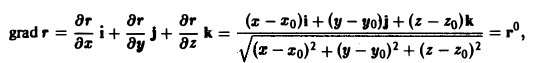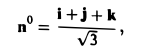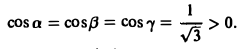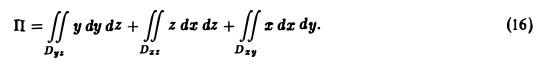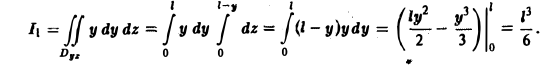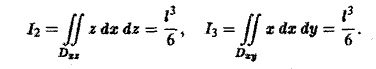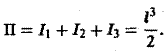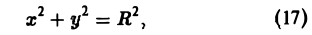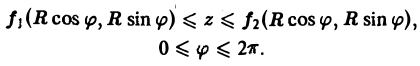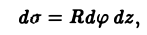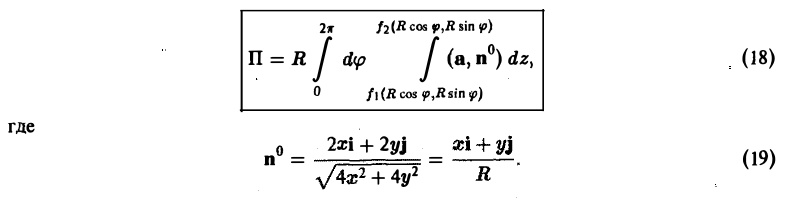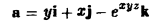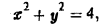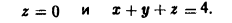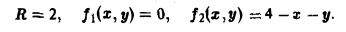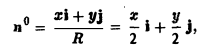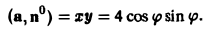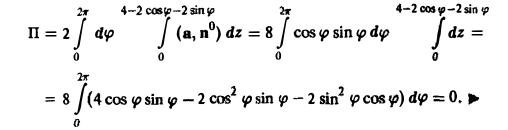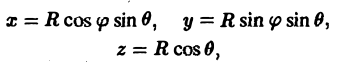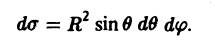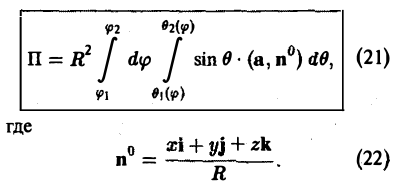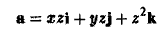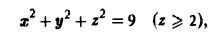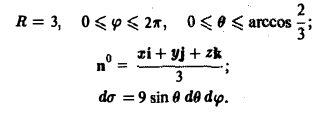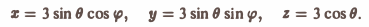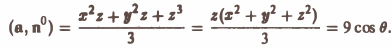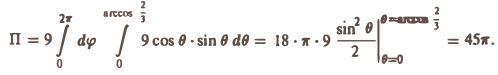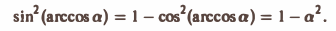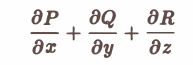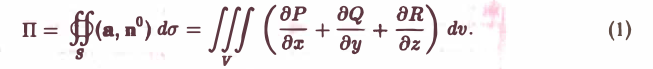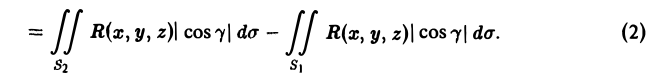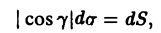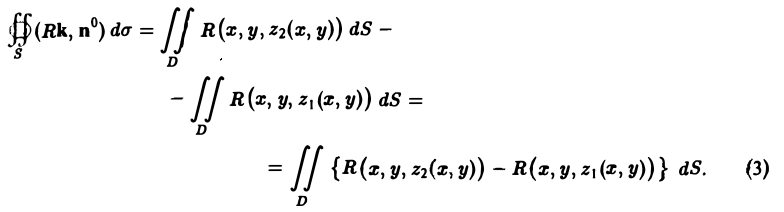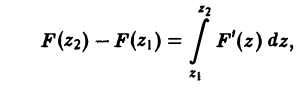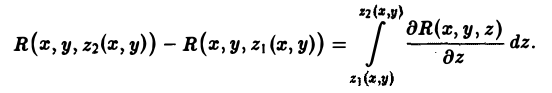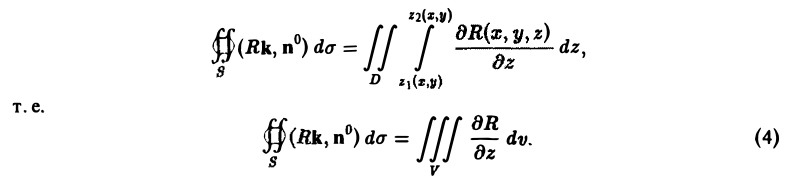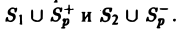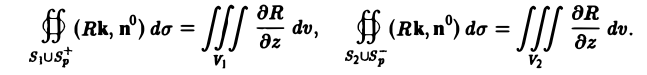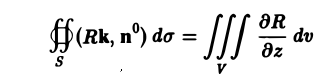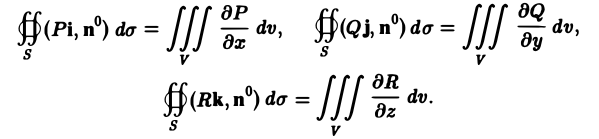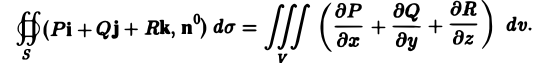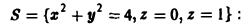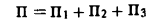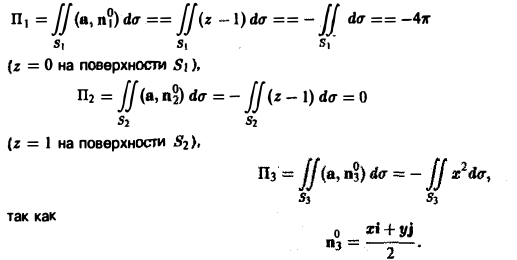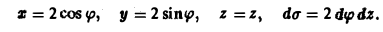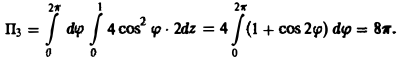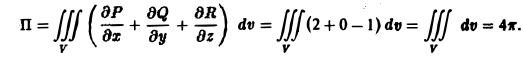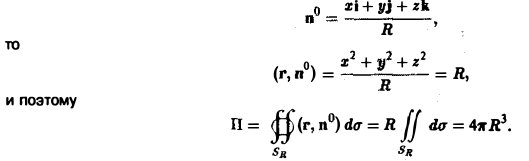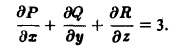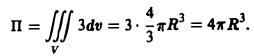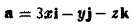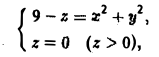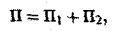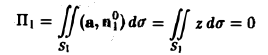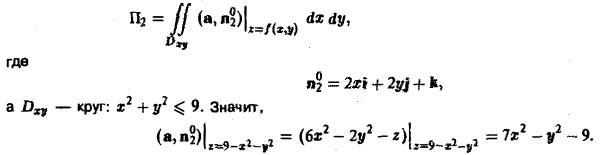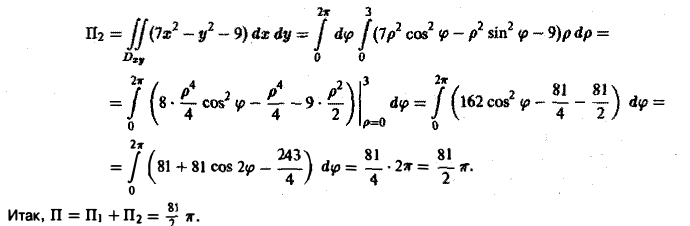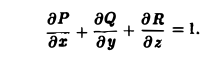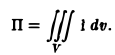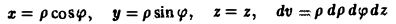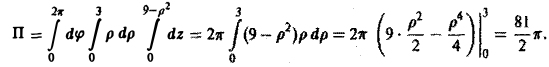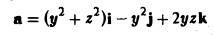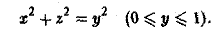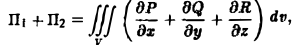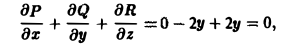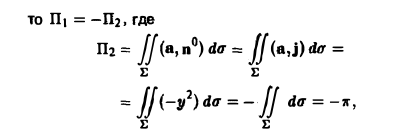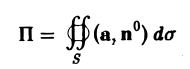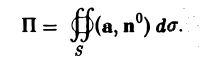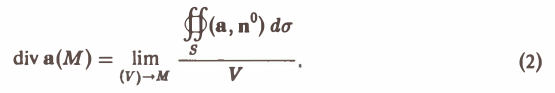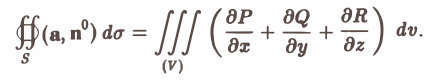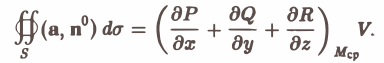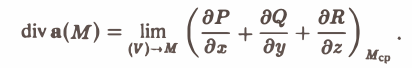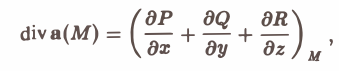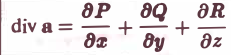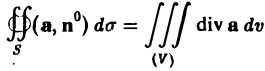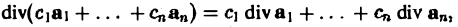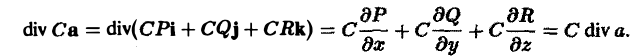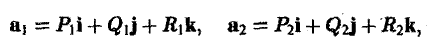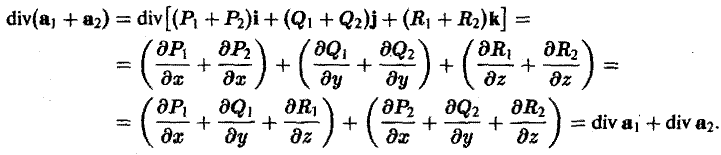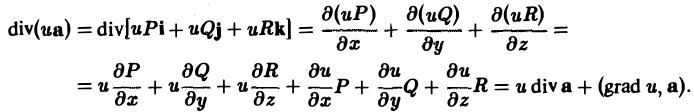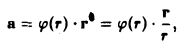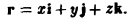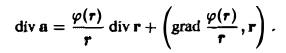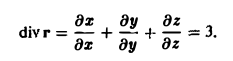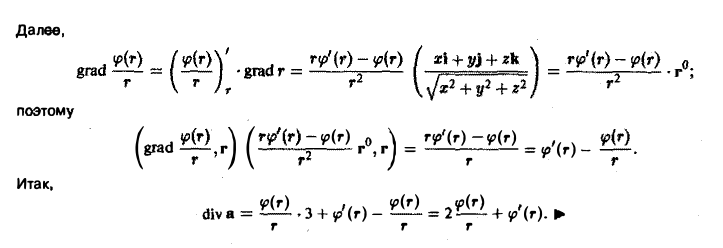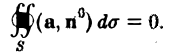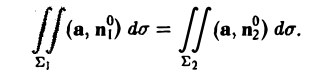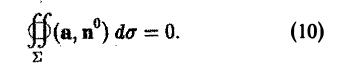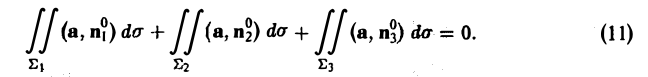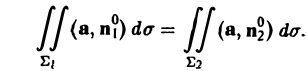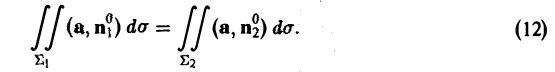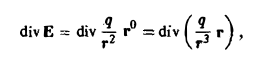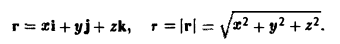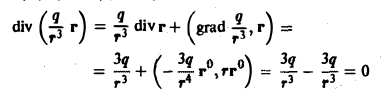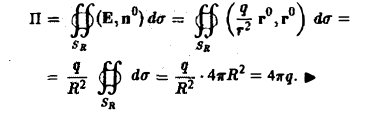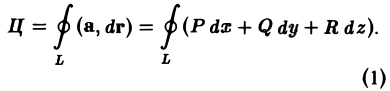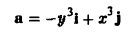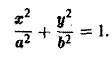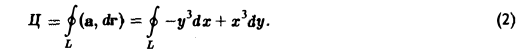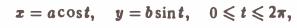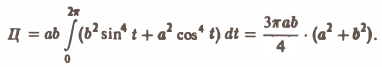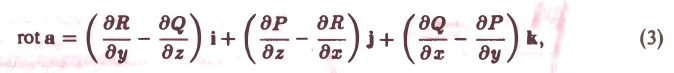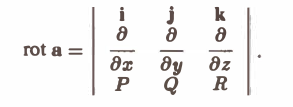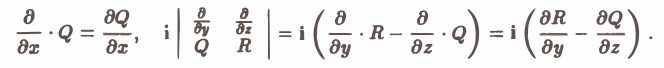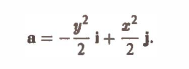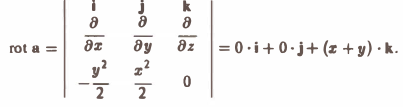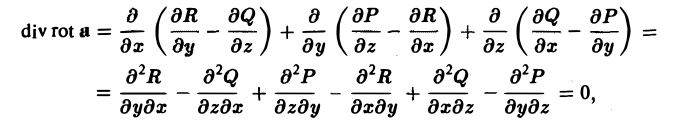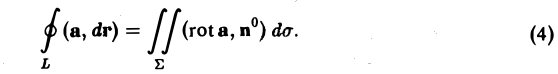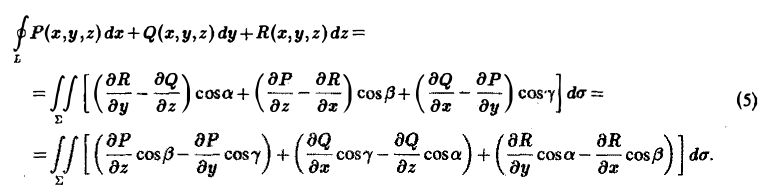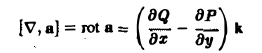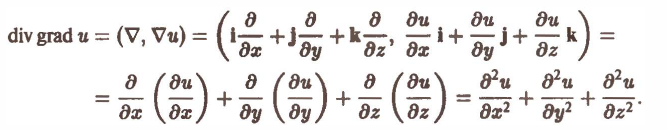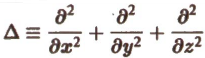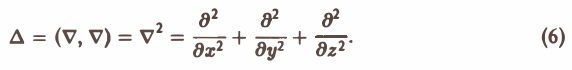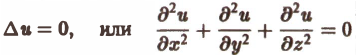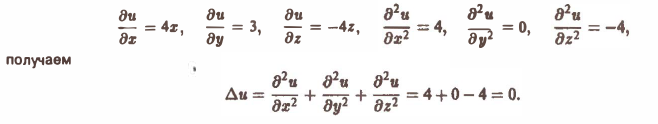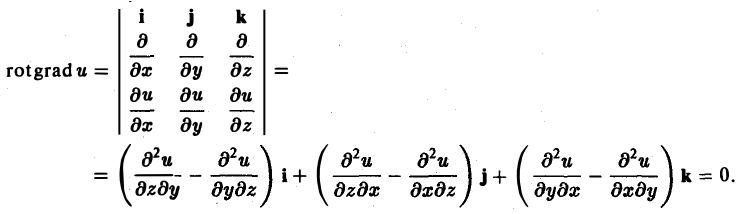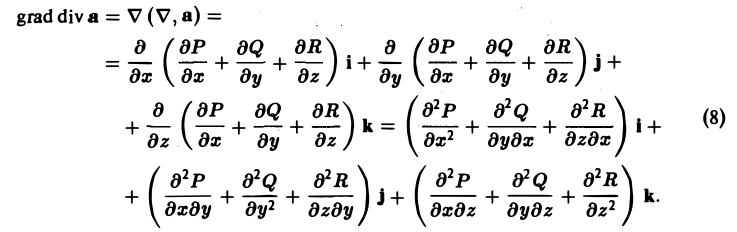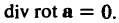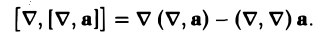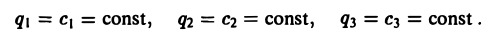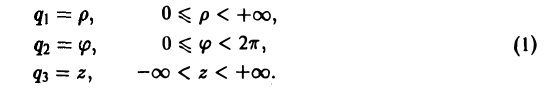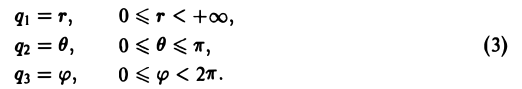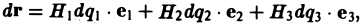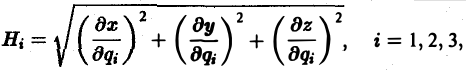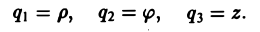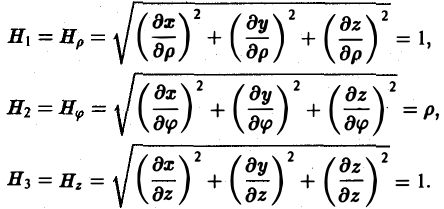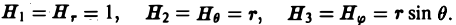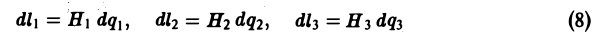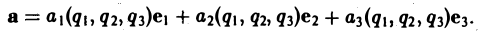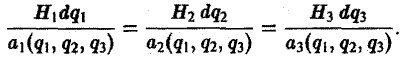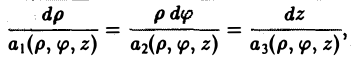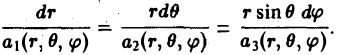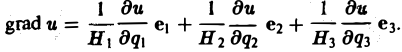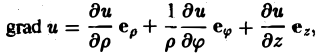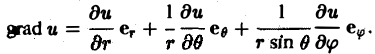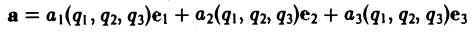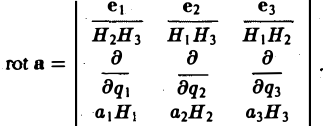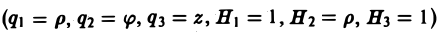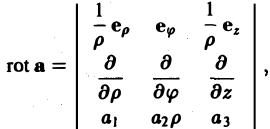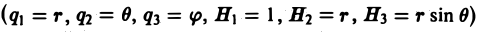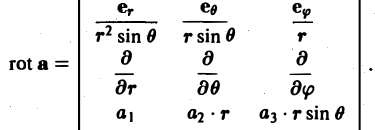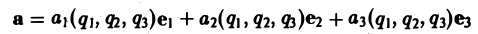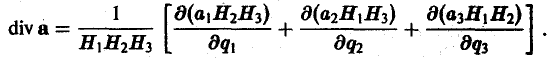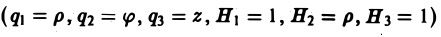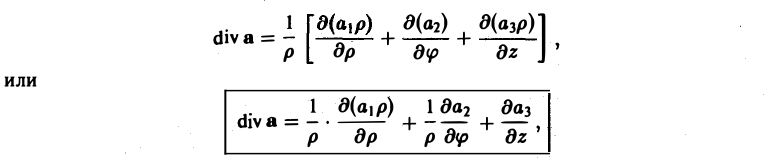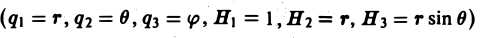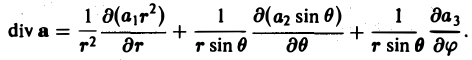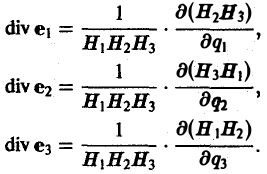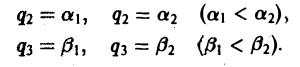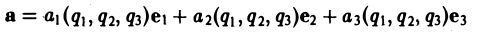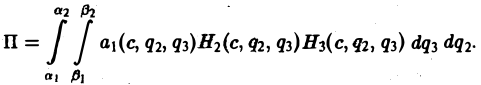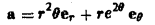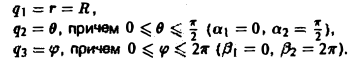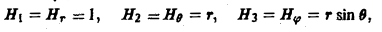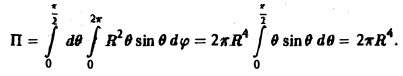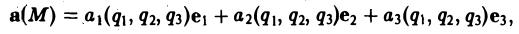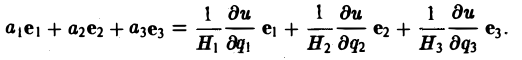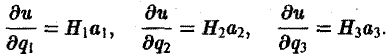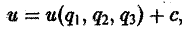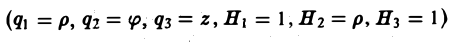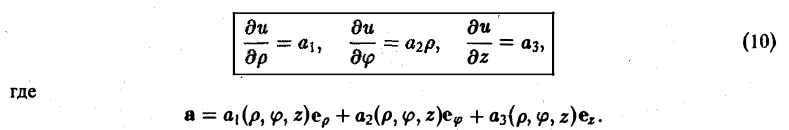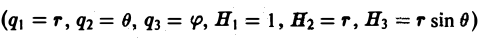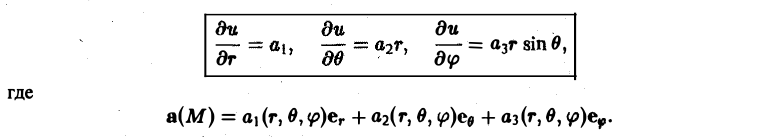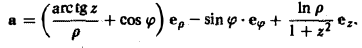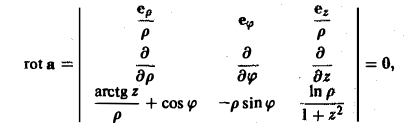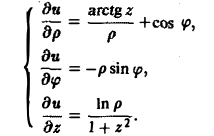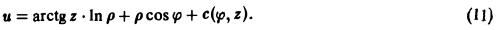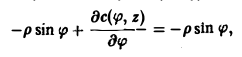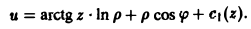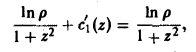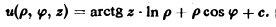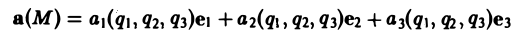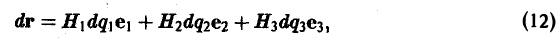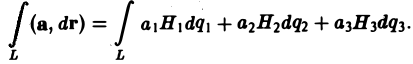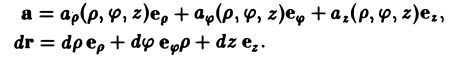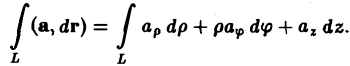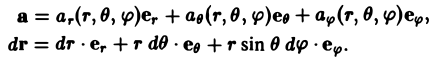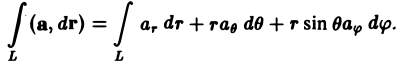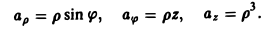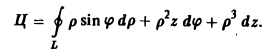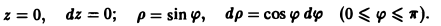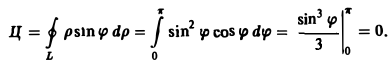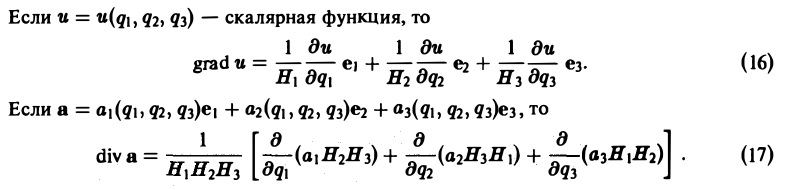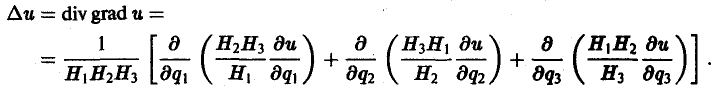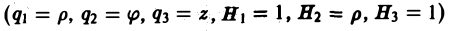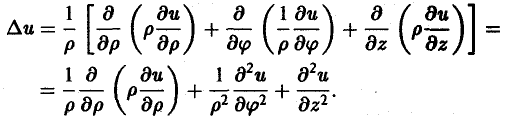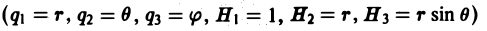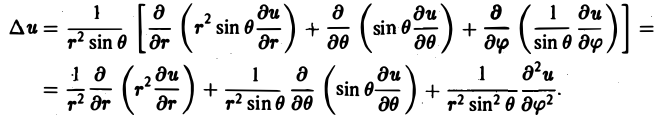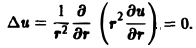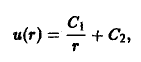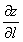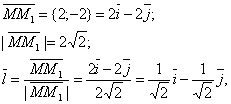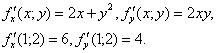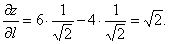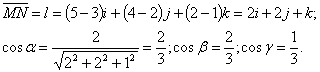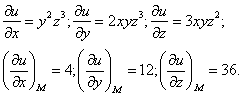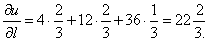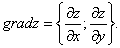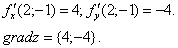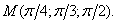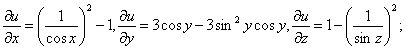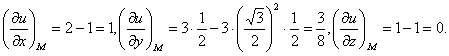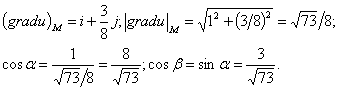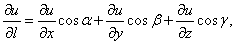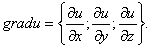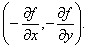Длина вектора градиента в точке

Градиент функции — это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:

где , , — частные производные функции по переменным , , соответственно.

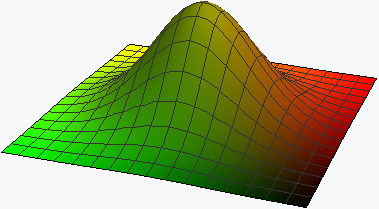
Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .

Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.

Видео:Нахождение градиента функции в точкеСкачать

Найти длину вектора градиента

Видео:Градиент в точке.Скачать

Градиент функции онлайн

Градиент функции — это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:

где , , — частные производные функции по переменным , , соответственно.

Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .

Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.

Видео:10. ФНП. Градиент и производная по направлению функции двух переменных.Скачать

Векторный анализ с примерами решения и образцами выполнения

Векторный анализ — раздел математики, распространяющий методы математического анализа на векторы, как правило в двух- или трёхмерном пространстве. Объектами приложения векторного анализа являются: Векторные поля — отображения одного векторного пространства в другое.

Видео:ВМ. 9.5 Производная в точке по направлению вектора.Скачать

Скалярное поле. Поверхности и линии уровня. Производная по направлению

Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано иоде данной величины. Поле называется скалярным, если рассматриваемая величина скалярна, т.е. вполне характеризуется своим числовым значением. Например, поле температур.

Скалярное поле задается скалярной функцией точки и = f(М). Если в пространстве введена декартова система координат, то и есть функция трех переменных х, у, z — координат точки М:

u = f(x,y,z). (1)

Определение:

Поверхностью уровня скалярного поля называется множество точек, в которых функция f(М) принимает одно и то же значение. Уравнение поверхности уровня

f(x, y, z) = с = const. (2)

Пример:

Найти поверхности уровня скалярного поля

Согласно определению уравнением поверхности уровня будет

Это уравнение сферы (с ≠ 0) с центром в начале координат.

Скалярное поле называется плоским, если во всех плоскостях, параллельных некоторой плоскости, поле одно и то же. Если указанную плоскость принять за плоскость хОу, го функция поля не будет зависеть от координаты г, т. е. будетфункцией только аргументов х и у,

u=f(x, y). (3)

Плоское поле можно характеризовать с помощью линий уровня — множества точек плоскости, в которых функция f(x, у) имеет одно и то же значение. Уравнение линии уровня —

f(х, у) = с = const. (4)

Пример:

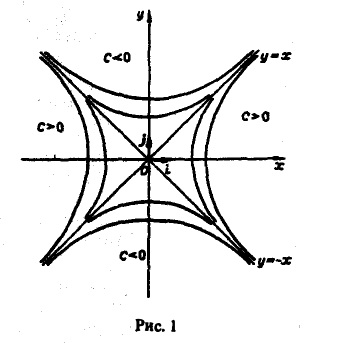
Найти линии уровня скалярного поля

Линии уровня задаются уравнениями

При с = О получаем пару прямых у = х, у = -х. При с ≠ 0 получаем семейство гипербол (рис. 1).

Производная по направлению

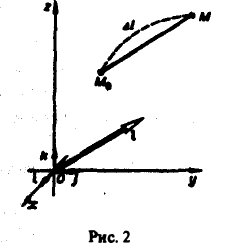
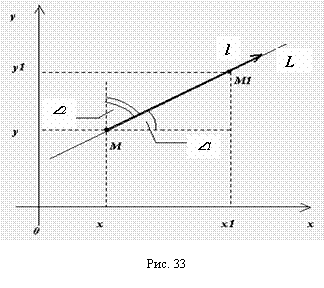
Пусть имеется скалярное поле, определяемое скалярной функцией и = f(M). Возьмем точку М0 и выберем направление, определяемое вектором I. Возьмем другую точку М так, чтобы вектор М0М был параллелен вектору 1 (рис.2). Обозначим длину вектора МоМ через ∆l, а приращение функции f(М) — f(Mo), соответствующее перемещению ∆l, через ∆и. Отношение

определяет среднюю скорость изменения скалярного поля на единицу длины поданному направлению I.

Пусть теперь ∆l стремится к нулю так, чтобы вектор М0М все время оставался параллельным вектору I.

Определение:

Если при ∆l —> 0 существует конечный предел отношения (5), то его называют производной функции и = f(M) в данной точке М0 по данному направлению I и обозначают символом

Так что, по определению,
(6)

Это определение не связано с выбором системы координат, т. е. Hocит вариантный характер.

Найдем выражение для производной по направлению в декартовой системе координат. Пусть функция f(М) = f(х, у, z) дифференцируема в точке Мо(хо, yо, zо). Рассмотрим значение f(M) в точке М(х0 + ∆х,у0 + ∆y, zo + ∆z). Тогда полное приращение функции можно записать в следующем виде:

означают, что частные производные вычислены в точке Мо. Отсюда (7)

Здесь величины 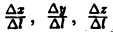суть направляющие косинусы вектора МоМ = ∆xi + ∆yj + ∆zk. Так как векторы МоМ и I сонаправлены (М0М ↑↑ I), то их направляющие косинусы одинаковы:

Так как M —» Mo, оставаясь все время на прямой, параллельной вектору I, то углы а, β, γ постоянны, а потому

Окончательно из равенств (7) и (8) получаем

Замечание:

Частные производные 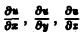являются производными функции и по направлениям координатных осей Ox, Оу, Oz соответственно.

Пример:

Найти производную функции

в точке Mo(3,0,2) по направлению к точке M1(4,1, 3).
Имеем

Вектор МoМ = имеет длину |МоМ| = /3. Его направляющие косинусы:

По формуле (9) будем иметь

Тот факт, что 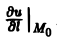>0, означает, что скалярное поле в точке М0 в данном направлении возрастает.
Для плоского поля U = f(x, у) производная по направлению 1 в точке Мо(х0, у0) вычисляется по формуле (10)

где а — угол, образованный вектором I с осью Ох.

Замечание:

Формула (9) для вычисления производной по направлению I в данной точке М0 остается в силе и тогда, когда точка М стремится к точке Мо по кривой, для которой вектор I является касательным в точке Мо.

Пример:

Вычислить производную скалярного поля

и = arctg(xy)

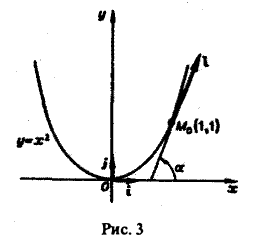
в точке Mo(1, 1), принадлежащей параболе у = х2, по направлению этой кривой (в направлении возрастания абсциссы).

Пусть касательная к параболе в точке Мо образует с осью Ох угол a. Тогда tga =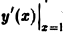= 2, откуда направляющие косинусы касательной

Вычислим значения 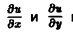в точке Mo(1, 1). Имеем

Теперь по формуле (10) получаем

Пример:

Найти производную скалярного поля и = In(xy + yz + zx) в точке Mo(0, 1, 1) по направлению окружности

Векторное уравнение окружности имеет вид

Находим единичный вектор т касательной к окружности

Точке Mo(0,1, 1) соответствует значение параметра t= π/2 Значение т в точке Мо будет равно

Отсюда получаем направляющие косинусы касательной к окружности в точке Mо: cos a = — 1, cos β = 0, cos γ = 0.

Вычислим значения частных производных данного скалярного поля в точке Mo(0, 1, 1)

Значит, искомая производная

Градиент скалярного поля

Пусть скалярное поле определяется скалярной функцией

u = f(x, y. z),

которая предполагается дифференцируемой.

Определение:

Градиентом скалярного поля u в данной точке М называется вектор, обозначаемый символом grad и и определяемый равенством
(1)

Ясно, что этот вектор зависит от функции f, так и от точки М, в которой вычисляется ее производная.
Пусть I° — единичный вектор в направлении I, т. е.

Тогда формулу для производной по направлению можно записать в следующем виде:
(3)

тем самым производная от функции и по направлению I равна скалярному произведению градиента функции u(M) на орт I° направления I.

Основные свойства градиента

Теорема:

Градиент скалярного поля перпендикулярен к поверхности уровня (или к линии уровня, если поле плоское).
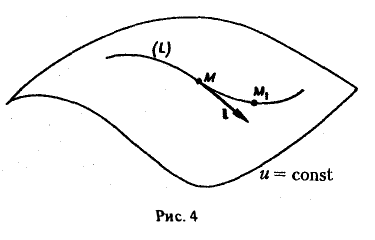
Проведем через произвольную точку М поверхность уровня и = const и выберем на этой поверхности гладкую кривую L, проходящую через точку М (рис. 4). Пусть 1 — вектор, касательный к кривой L в точке М.

Так как на поверхности уровня и(М) = и(М1) для любой точки М1 ∈ L, то

С другой стороны, 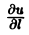= (grad и, I°). Поэтому (grad и, I°) = 0. Это означает, что векторы grad и и I° ортогональны, grad u ⊥ I°.

Итак, вектор grad и ортогонален к любой касательной к поверхности уровня в точке М. Тем самым он ортогонален к самой поверхности уровня в точке М.

Теорема:

Градиент направлен в сторону возрастания функции поля.

Ранее мы доказали, что градиент скалярного поля направлен по нормали к поверхности уровня, которая может быть ориентирована либо в сторону возрастания функции и(М), либо в сторону ее убывания.

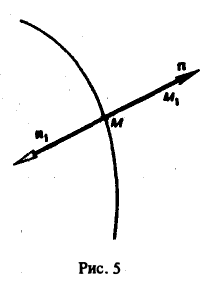
Обозначим через п нормаль к поверхности уровня, ориентированную в сторону возрастания функции и(М), и найдем производную функции и в направлении этой нормали (рис. 5). Имеем

Так как по условию и(М1) > и(М), то и(М1) — и(М) > 0, и поэтому

Отсюда следует, что grad и направлен в ту же сторону, что и выбранная нами нормаль п, т.е. в сторону возрастания функции и(М).

Теорема:

Длина градиента равна наибольшей производной по направлению в данной точке поля,

(здесь mах 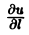берется по всевозможным направлениям в данной точке М поля).
Имеем

где φ — угол между векторами I и grad n. Так как наибольшее значение cos φ равно 1, то наибольшим значением производной 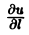как раз и является |grad и|.

Пример:

Найти направление наибольшего изменения скалярного поля

и = ху + yz + zx

в точке Mо(1, 1, 1), а также величину этого наибольшего изменения в указанной точке.

Направление наибольшего изменения скалярного поля указывается вектором grad u(M). Имеем grad u(М) = (у + z)i + (х + г)j + (у + х)к, так что

Этот вектор определяет направление наибольшего возрастания поля в точке Мо(1,1,1). Величина наибольшего изменения поля в этой точке равна

Инвариантное определение градиента

Величины, характеризующие свойства изучаемого объекта и не зависящие от выбора системы координат, называются инвариантами данного объекта. Например, длина кривой — инвариант этой кривой, а угол касательной к кривой с осью Ох — не инвариант.

Основываясь на доказанных выше трех свойствах градиента скалярного поля, можно дать следующее инвариантное определение градиента.

Определение:

Градиент скалярного поля есть вектор, направленный по нормали к поверхности уровня в сторону возрастания функции поля и имеющий длину, равную наибольшей производной по направлению (в данной точке).
Пусть п° — единичный вектор нормали, направленный в сторону возрастания поля. Тогда

Пример:

Найти градиент расстояния

где Мo(хo,уo,zo) — некоторая фиксированная точка, а М(х,у,z) — текущая.

где r° — единичный вектор направления MoM.

Правила вычисления градиента

1. grad си(М) = с grad и 0), x=0, у — 0, z = 0 (угол γ — острый) (рис. 17).
   Имеем

Значит, перед всеми интегралами в формуле (15) следует взять знак « + ». Полагая Р = у, Q = z, R = х, получим

Вычислим первый интеграл в правой части формулы (16). Область Dyz — треугольник ВОС в плоскости yOz, уравнение стороны ВС: y+z = l, 0 ≤ у ≤ I. Имеем

Значит, искомый лоток равен

Метод введения криволинейных координат на поверхности

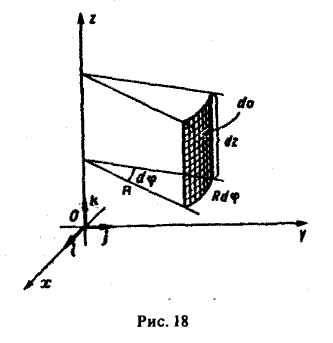
Если поверхность S является частью кругового цилиндра или сферы, при вычислении потока удобно, не применяя проектирования на координатные плоскости, ввести на поверхности криволинейные координаты.

А. Поверхность S является частью кругового цилиндра

ограниченного поверхностями z = f1(x,y) и z = f2(х. у), где f1(x. y) ≤ f2(x, y) (рис. 18). Полагая х = R cos φ, у = R sin φ, z = z, будем иметь

Элемент площади поверхности выражается так:

и поток вектора а через внешнюю сторону поверхности S вычисляется по формуле:

Пример:

Найти поток вектора

через внешнюю сторону поверхности цилиндра

то скалярное произведение (а, п°) на цилиндре (х = 2 cos φ, у = 2 sin φ, z = z) равно:

Тогда по формуле (18) получим

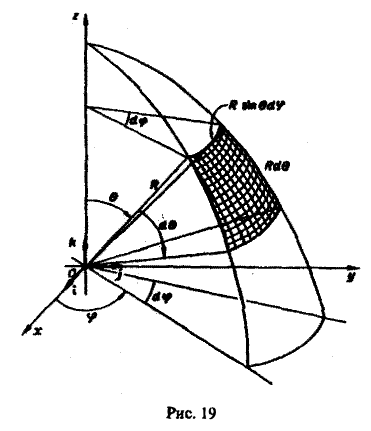
В. Поверхность S является частью сферы

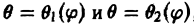
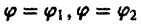
ограниченной коническими поверхностями, уравнения которых в сферических координатах имеют вид и полуплоскостями (рис. 19).Точки данной сферы описываются соотношениями

где 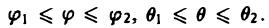Поэтому элемент площади

В этом случае поток векторного поля а через внешнюю часть поверхности S вычисляется по формуле

Пример:

Найти поток вектора

через внешнюю часть сферы

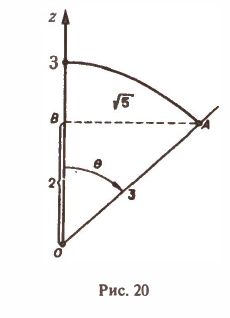
отсеченную плоcкостью z = 2 (рис. 20).

В данном случае имеем

Тогда скалярное произведение (а, п°) выразится так:

По формуле (21) получим

Замечание:

Здесь мы воспользовались формулой

Видео:Длина вектора через координаты. 9 класс.Скачать

Поток вектора через замкнутую поверхность. Теорема Гаусса—Остроградского

Теорема:

Если в некоторой области G пространства R3 координаты вектора

а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k

непрерывны и имеют непрерывные частные производные 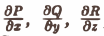, то поток вектора а через любую замкнутую кусочно-гладкую поверхность S, лежащую в области G, равен тройному интегралу от

по области V, ограниченной поверхностью S:

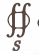
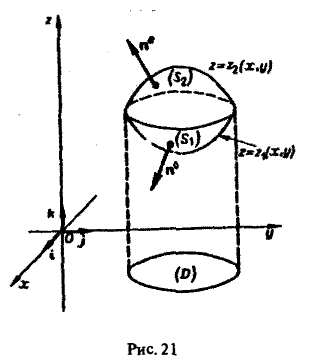
Здесь п0 — орт внешней нормали к поверхности, а символ означает поток через замкнутую поверхность S. Эта формула называется формулой Гаусса—Остроградского.

Рассмотрим сначала вектор а, имеющий только одну компоненту а = R(x, у, z)k, и предположим, что гладкая поверхность S пересекается каждой прямой, параллельной оси Oz, не более чем в двух точках. Тогда поверхность S разбивается на две части S1 и S2, однозначно проектирующиеся на некоторую область D плоскости хОу (рис.21).

Внешняя нормаль к поверхности S2 образует острый угол γ с осью Oz, а внешняя нормаль к поверхности S1 образует тупой угол с осью Oz. Поэтому cos γ = (п°, к) > 0 на S2 и cos γ

Пусть dσ — элемент площади на поверхности S. Тогда

где dS — элемент площади области D. Сведем интегралы по поверхности к двойным интеграл ам по области D плоскости хОу, на которую проектируются поверхности S1 и S2. Пусть S2 описывается уравнением z = z2(x, у), а S, — уравнением z = z1(x, у). Тогда

Так как приращение непрерывно дифференцируемой функции можно представить как интеграл от ее производной

то для функции R(x, у, z) будем иметь

Пользуясь этим, получаем из формулы (3)

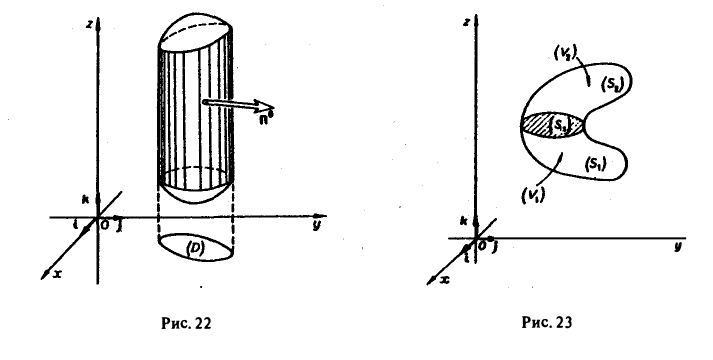
Если поверхность S содержит часть цилиндрической поверхности с образующими, параллельными оси Oz (рис. 22), то на этой части поверхности (Rk, п°) = 0 и интеграл ∫∫ (Rk, n°) dσ по ней равен нулю. Поэтому формула (4) остается справедливой и для поверхностей, содержащих указанные цилиндрические части.

Формула (4) переносится и на случай, когда поверхность 5 пересекается вертикальной прямой более, чем в двух точках (рис. 23).

Разрежем область V на части, поверхность каждой из которых пересекается вертикальной прямой не более чем в двух точках, и обозначим через Sp поверхность разреза. Пусть S1 и S2 — те части поверхности S, на которые она разбивается разрезом Sp,a V1 и V2 — соответствующие части области V, ограниченные поверхностями

Здесь Sp+ означает, что вектор нормали к разрезу Sp направлен вверх (образует с осью Oz острый угол), a Sp — — что этот вектор нормали направлен вниз (образует с осью Oz тупой угол). Имеем:

Складывая полученные равенства и пользуясь аддитивностью потока и тройного интеграла, получим

(интегралы по разрезу Sp взаимно уничтожаются). Рассмотрим, наконец, вектор

Для каждой компоненты Pi, Qj, Rк мы можем написать формулу, аналогичную формуле (4) (все компоненты равноправны). Получим

Складывая эти равенства и пользуясь линейностью потока и тройного интеграла, получаем формулу Гаусса—Остроградского

Пример:

Вычислить поток вектора

а = 2xi — (z — 1)k

через замкнутую поверхность

1) по определению, 2) по формуле Остроградского.

1) Поток вектора а равен сумме

Перейдем на цилиндре к криволинейным координатам

Следовательно, П = -4π + 0 + 8π = 4π.

2) По формуле Гаусса—Остроградского имеем

Пример:

Вычислить поток радиус-вектора

r = xi + yj + zk

через сферу радиуса R с центром в начале координат:

1) по определению; 2) по формуле Остроградского.

1) Так как для сферы

2) Сначала находим

Пример:

Вычислить поток вектора

через замкнутую поверхность S, заданную условиями:

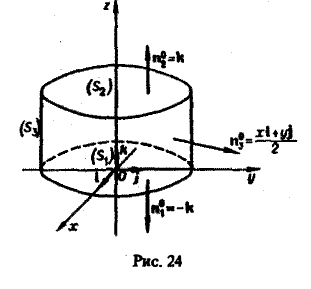
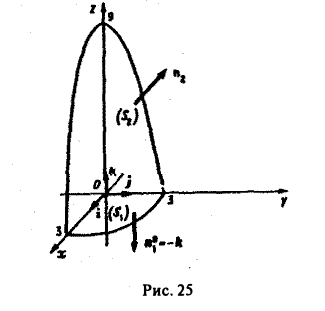
1) по определению; 2) по формуле Остроградстого (рис.25).

(на S1 имеем z = 0),

Переходя к цилиндрическим координатам

и замечая, что z = 9 — р на поверхности S, имеем

Замечание:

При вычислении потока через незамкнутую поверхность часто бывает удобно подходящим образом дополнить ее до замкнутой и воспользоваться формулой Гаусса—Оcтроградского.

Пример:

Вычислить поток вектора

через поверхность S:

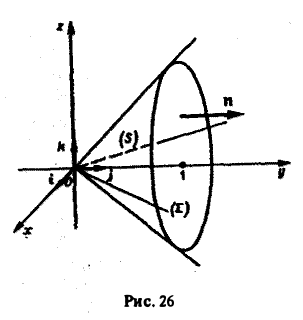
Заданная поверхность S есть конус с осью Оу (рис. 26).

Замкнем этот конус куском Σ плоскости у = I. Тогда, обозначая через П1 искомый поток, а через П2 поток по поверхности Σ, будем иметь

где V — объем конуса, ограниченного поверхностями S и Σ.
Так как

т.к. на поверхности Σ выполняется равенство у = 1. Следовательно, П1 = π.

Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Дивергенция векторного поля. Соленоидальные (трубчатые) поля

Пусть S — замкнутая поверхность. Рассмотрим поле скоростей v течения жидкости и вычислим поток жидкости через поверхность 5. Если он положителен, то это означает, что из той части пространства, которая ограничена поверхностью S, вытекает больше жидкости, чем втекает в нее. В этом случае говорят, что внутри S имеются источники (выделяющие жидкость). Напротив, если поток отрицателен, то внутрь S втекает больше жидкости, чем вытекает из нее. В этом случае говорят, что внутри S имеются стоки (поглощающие жидкость).

Тем самым, величина

позволяет судить о природе части векторного поля, заключенного внутри поверхности S, а именно, о наличии источников или стоков внутри нее и их производительности (мощности).

Понятие о потоке вектора через замкнутую поверхность приводит к понятию дивергенции, или расходимости поля, которое дает некоторую количественную характеристику поля в каждой его точке.

Пусть М — изучаемая точка поля. Окружим ее поверхностью S произвольной формы, например, сферой достаточно малого радиуса. Область, ограниченную поверхностью 5, обозначим через (V), а ее объем через V.

Вычислим поток вектора а через поверхность S. Имеем

Составим отношение этого потока П к величине объема V,

Так как числитель представляет собой производительность источников (стоков) внутри области (V), то отношение (1) дает среднюю производительность единицы объема.

Определение:

Если отношение (1) имеет конечный предел, когда область (V) стягивается в точку М, то этот предел называют дивергенцией векторного поля (дивергенцией вектора а) в точке М и обозначают div а(М). То есть по определению

Дивергенция векторного поля есть скалярная величина (числитель и знаменатель дроби (2) суть скалярные величины).

Если diva(M) > 0, то в точке М расположен источник, если diva(M)

Пользуясь теоремой о среднем для тройного интеграла, получим

Подставляя это выражение в формулу (2), определяющую дивергенцию, найдем

Когда область (V) стягивается в точку М, то и точка Мcp стремится к точке М и, в силу предположенной непрерывности частных производных, получаем

(все величины в формуле (3) вычисляются водной и той же точке).

Формула (3) дает выражение дивергенции в декартовых координатах. Попутно доказано само существование дивергенции вектора а при условии, что производные 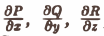непрерывны.

Используя формулу (3) для дивергенции, запишем формулу Гаусса—Остроградского в векторной форме. Имеем
(4)

— поток вектора а через замкнутую поверхность S равен тройному интегралу от дивергенции вектора а по области (V), ограниченной поверхностью S.

Правила вычисления дивергенции

1, Дивергенция обладает свойством линейности
(5)

где С1,…, Сп — постоянные числа.

а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k

и С — постоянное число. Тогда

2. Дивергенция постоянного вектора с равна нулю

div e = 0. (6)

3. Дивергенция произведения скалярной функции и(М) на вектор а(М) вычисляется по формуле

div(ua) = u diva + (gprad u,a). (7)

Пример:

Найти дивергенцию вектора

где r = |r| — расстояние от начала координат до переменной точки М(х,у,z),

По формуле (7) имеем

Так как r = xi + уj + zk. то

Трубчатое (соленоидальное) поле

Если во всех точках некоторой области G дивергенция векторного поля, заданного в этой области, равна нулю

div а ≡ 0, (8)

то говорят, что в этой области поле соленоидальное (или трубчатое).

Из формулы Гаусса—Остроградского вытекает, что в трубчатом поле поток вектора через любую замкнутую поверхность S, лежащую в этом поле, равен нулю
(9)

Свойства трубчатого поля

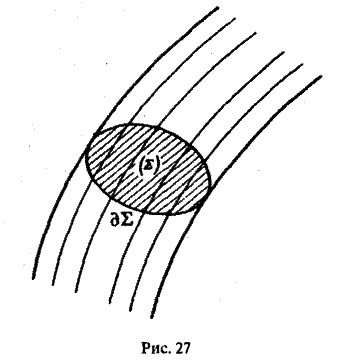
Рассмотрим в области, где задано поле вектора а, какую-нибудь площадку Σ (рис.27). Назовем векторной трубкой совокупность векторных линий, проходящих через границу γ = θΣ этой площадки. Пусть Σ1 — некоторое сечение векторной трубки. Выберем вектор нормали щ к сечению Σ1 так, чтобы он был направлен в ту же сторону, что и вектор а поля.

Теорема:

В трубчатом поле поток вектора а через любое сечение векторной трубки один и тот же.

Пусть Σ1 и Σ2 —непересекающиеся сечения одной и той же векторной трубки. Надо доказать, что

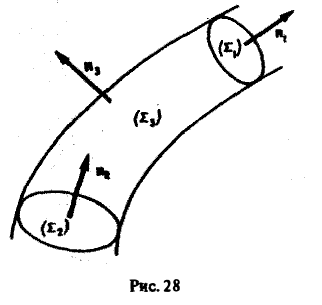
Обозначим через Σ3 часть поверхности векторной трубки, заключенную между сечениями Σ1 и Σ2. Поверхности Σ1, Σ2, Σ3 вместе образуют замкнутую поверхность Σ (рис.28).

Так как по условию поле вектора а — трубчатое, то

В силу аддитивности потока соотношение (10) можно переписать так:

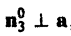
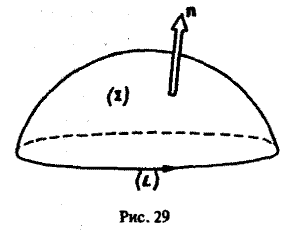
В точках поверхности Σ3, составленной из векторных линий, имеем , так что (а, п°3) = 0 на Σз, и значит, последний интеграл в левой части (11) равен нулю. Таким образом, из (11) находим

Пусть поверхность Σ имеет ориентированный замкнутый контур L своей границей. Будем говорить, что поверхность Σ натянута на контур L. Вектор нормали п к поверхности Σ будем ориентировать так, чтобы из конца нормали обход контура L был виден против часовой стрелки (рис. 29).

Теорема:

В трубчатом поле поток вектора а через любую поверхность, натянутую на данный контур, один и тот же:

Замечание:

В трубчатом поле векторные линии могут быть либо замкнутыми кривыми, либо иметь концы на границе области, где поле задано.

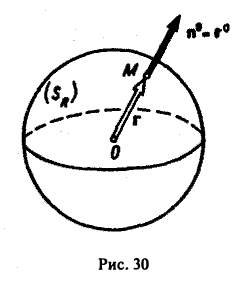
Пример:

Рассмотрим силовое поле, создаваемое точечным зарядом q, помешенным в начале координат. Вычислим дивергенцию вектора Е напряженности

Пользуясь формулой (7), получим

для r ≠ 0. Таким образом, поле вектора Σ, заданного формулой (13), будет трубчатым в любой области G, не содержащей точки O(0,0,0).

Вычислим поток вектора Σ через сферу Sr радиуса R с центром в начале координат O(0,0,0) (рис.30).

Замечание:

Можно показать, что поток вектора (13) через любую замкнутую поверхность Σ, охватывающую точку O(0,0,0), всегда равен 4 πg.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Циркуляция векторного поля. Ротор вектора. Теорема Стокса

Пусть в некоторой области G задано непрерывное векторное поле

а(М) = Р(х, у, х)i + Q(x, у, z)j + R(х, у, z)k

и замкнутый ориентированный контур L.

Определение:

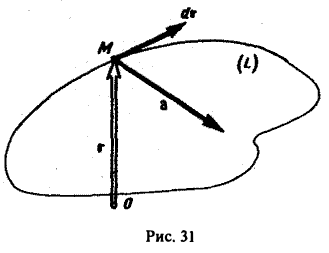
Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от вектора а по контуру L

Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, определяемым ориентацией контура (рис. 31) символ 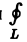означает, что интеграл берется по замкнутому контуру L.

Пример:

Вычислить циркуляцию векторного поля

вдоль эллипса L:

По определению циркуляции имеем

Параметрические уравнения данного эллипса имеют вид:

и, значит, dx = -a sin tdt, dy = b cos tdt. Подставляя эти выражения в формулу (2), найдем

Видео:Вектор-градиент (теория)Скачать

Ротор (вихрь) векторного поля

Рассмотрим поле вектора

а(М) = Р(х, у, z)i + Q(x, у, z)j + R(х, у, z)k,

Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам.

Определение:

Ротором вектора а(M) называется вектор, обозначаемый символом rot а и определяемый равенством

или, в символической, удобной для запоминания форме,

Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,

Определение:

Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называется безвихревым.

Пример:

Найти ротор вектора

Согласно формуле (3) имеем

Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим

div rot a = 0. (3′)

Таким образом, поле вектора rot а соленоидально.

Теорема Стокса:

Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L,

При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Σ, и что ориентация орта нормали п° к поверхности Σ С G согласована с ориентацией контура L так, что из конца нормали обход контура в заданном направлении виден совершающимся против часовой стрелки.

Учитывая, что а = Pi + Qj + Rk, n° = cos ai + cos βj + cos γk, и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде:

Рассмотрим сначала случай, когда гладкая поверхность Σ и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур λ соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура λ. Для определенности будем считать, что контур L ориентирован так, что поверхность Σ остается слева, так что веkтор нормали п к поверхности Σ составляет с осью Oz острый угол γ (cos γ > 0).

Пусть z = φ не будет, вообще говоря, перпендикулярным вектору а (впрочем, для плоского поля а = Р(х, y)i + Q(x, y)j вектор

перпендикулярен плоскости хОу, а значит, и вектору а).

Не имеет смысла и понятие коллинеарности по отношению к символическому вектору ∇. Например, выражение [∇ φ, ∇ ψ] где φ и ψ — скалярные функции, формально напоминает векторное произведение двух кoллинеарных векторов, которое всегда равно нулю. Однако в общем случае это не имеет места. В самом деле, вектор ∇ φ = grad φ направлен по нормали к поверхности уровня φ = const, а вектор ∇ ψ = grad ψ определяет нормаль к поверхности уровня ψ = const. В общем случае эти нормали не обязаны быть коллинеарными (рис. 40). С другой стороны, в любом дифференцируемом скалярном поле φ (х, у, z) имеем [∇ φ, ∇ ψ] = 0.

Эта примеры показывают, что с оператором «набла» нужно обращаться с большой осторожностью и при отсутствии уверенности в полученном результате его следует проверить аналитическими методами.

Видео:МОДУЛЬ ВЕКТОРА длина вектора 10 и 11 классСкачать

Дифференциальные операции второго порядка. Оператор Лапласа

Дифференциальные операции второго порядка получаются в результате двукратного применения оператора ∇.

1, Пусть имеем скалярное поле и = и(x,y,z). В этом поле оператор ∇ порождает векторное поле

∇u = grad и.

В векторном поле grad и можно определить две операции:

( ∇, ∇u) = div grad u, (1)

что приводит к скалярному полю, и

[ ∇, ∇m] = rot grad u, (2)

что приводит к векторному полю.

2. Пусть задано векторное поле а = Pi + Qj + Rk. Тогда оператор (2) порождает в нем скалярное поле

(∇, а) = div a.

В скалярном поле div а оператор ∇ порождает векторное поле

∇ (∇,a) = grad div а. (3)

3. В векторном поле а = Pi + Qj + Rк оператор ∇ порождает также векторное поле

[∇, а] = rot a.

Применяя к этому полю снова оператор ∇, получим:

а) скалярное поле

(∇, [∇, а]) = div rot а, (4).

б) векторное поле

(∇, [∇, а]) = rot rot а. (5)

Формулы (1)-(5) определяют так называемые дифференциальные операции второго порядка.

Выберем в пространстве прямоугольную декартову систему координат Oxyz и рассмотрим каждую из формул (1)-(5) более подробно.

1, Предполагая, что функция и(х, у, z) имеет непрерывные вторые частные производные по х, у и z, получим

называется оператором Лапласа, или лапласианом. Его можно представить как скалярное произведение оператора Гамильтона ∇ на самого себя, т.е.

Оператор ∆ (дельта) играет важную роль в математической физике. Уравнение (6)

называется уравнением Лапласа. С его помощью описывается, например, стационарное распределение тепла.

Скалярное поле и(х, у, z), удовлетворяющее условию ∆и = 0, называется лапла-совым или гармоническим полем.

Например, скалярное поле и = 2х 2 + Зу — 2x 2 является гармоническим во всем трехмерном пространстве: из того, что

2. Пусть функция u(z, у, z) имеет непрерывные частные производные второго порядка включительно. Тогда

rot grad u ≡ 0. (7)

В самом деле, действуя формально, получим

rot grad и = [∇, ∇u] = [ ∇, ∇ ] u = 0,

ибо [∇, ∇] = 0 как векторное произведение двух одинаковых «векторов».

Тот же результат можно получить, используя выражения градиента и ротора в декартовых координатах

3. Пусть задано векторное поле

а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k,

координаты которого P, Q, R имеют непрерывные частные производные второго порядка. Тогда получим

4. При тех же условиях, что и в пункте 3, имеем (9)

Это соотношение уже было доказано ранее путем непосредственных вычислений. Здесь мы приведем его формальное доказательство, используя известную формулу из векторной алгебры

(А, [В, С]) = (С,[А,В])= (В, [С, А]).

div rot а = (∇, [∇, а]) = (а, [∇, ∇]) = О,

так как [∇, ∇] = 0 как векторное произведение двух одинаковых «векторов».

5. Покажем, наконец, что при тех же условиях, что и ранее,

rot rot а = grad div а — ∆а. (10)

rot rot а = [ ∇, [∇,a]),

то, полагая в формуле для двойного векторного произведения [А, [В, С]] = В(А, С) — (А, В)С,

А = ∇, B = ∇, С = а,

Но ( ∇, а) = div а и ( ∇, ∇) = ∆. Поэтому окончательно будем иметь

rot rot а = grad div а — ∆а,

где grad div а выражается по формуле (8), а ∆а для вектора а = Pi + Qj + Rk надо понимать так:

∆а = ∆Р • i + ∆Q • j + ∆R • k.

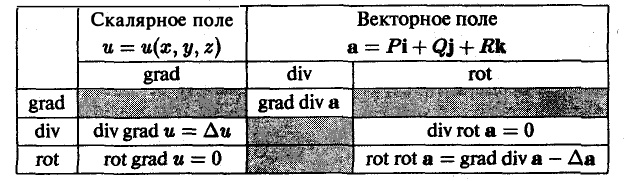
В заключение приведем таблицу дифференциальных операций второго порядка.

Заштрихованные прямоугольники означают, что соответствующая операция не имеет смысла (например, градиент от rot а).

Видео:ГрадиентСкачать

Понятие о криволинейных координатах

Во многих задачах бывает удобно определять положение точки простр анства не декартовыми координатами (х, у, z), а тремя другими числами (q1, q2, q3), более естественно связанными с рассматриваемой частной задачей.

Если задано правило, согласно которому каждой точке М пространства отвечает определенная тройка чисел (q1, q2, q3) и, обратно, каждой такой тройке чисел отвечает единственная точка М, то говорят, что в пространстве задана криволинейная координатная система. В этом случае величины q1, q2, q3 называют криволинейными координатами точки М.

Координатными поверхностями в системе криволинейных координат q1, q2, q3 называются поверхности

На координатных поверхностях одна из координат сохраняет постоянное значение. Линии пересечения двух координатных поверхностей называются координатными линиями.

В качестве примеров криволинейных координат рассмотрим цилиндрические и сферические координаты.

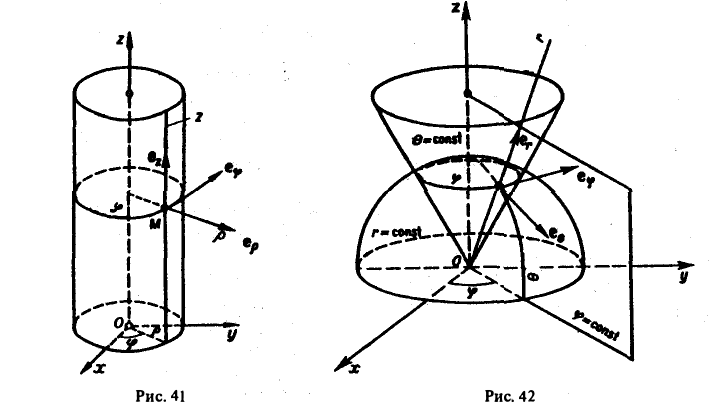
Цилиндрические координаты

В цилиндрических координатах положение точки М в пространстве определяется тремя координатами:

р = const — круговые цилиндры с осью Оz;

φ = const — полуплоскости, примыкающие к оси Oz;

z = const — плоскости, перпендикулярные оси Oz (рис. 41).

1) линии (р) — лучи, перпендикулярные оси Oz и имеющие начало на этой оси, т. е. линии пересечения координатных поверхностей φ = const, z = const;

2) линии (φ) — окружности с центрами на оси Oz, лежащие в плоскостях, перпендикулярных оси Oz;

3) линии (z) — прямые, параллельные оси Oz.

Связь декартовых координат точки (х, у, z) с цилиндрическими координатами (р, φ, z) задается формулами

x = p cos φ, y = p sin φ, z = z. (2)

Сферические координаты

В сферических координатах положение точки М в пространстве определяется следующими координатами:

Координатные поверхности (рис. 42):

r = const — сферы с центром в точке О;

θ = const — круговые полуконусы с осью Oz;

φ = const — полуплоскости, примыкающие к оси Oz.

1) линии (г) — лучи, выходящие из точки О;

2) линии (θ) — меридианы на сфере;

3) линии (φ) — параллели на сфере.

Связь декартовых координат (х, у, z) точки М с ее сферическими координатами (r, θ, φ) задается формулами

х = r cos φ sin θ,

у = r sin φ sin θ, (4)

z = r cos θ.

Введем единичные векторы e1, е2, е3 (орты), направленные по касательным к координатным линиям(q1),(q2),(q3)в тoчке М в сторону возрастания переменных q1,q2,q3 соответственно.

Определение:

Система криволинейных координат называется ортогональной, если в каждой точке М орты e1, е2, е3 попарно ортогональны.
В такой системе ортогональны и координатные линии, и координатные поверхности.
Примерами ортогональных криволинейных координат служат системы цилиндрических и сферических координат. Мы ограничимся рассмотрением только ортогональных систем координат.

Пусть r = r(q1, q2, q3) — радиус-вектор точки М. Тогда можно показать, что
(5)

— коэффициенты Ламэ данной криволинейной системы координат. Вычислим коэффициенты Ламэ для цилиндрических координат

Так как х = р cos φ, у = р sin φ, z = z, то
(6)

Аналогично для сферических координат имеем
(7)

являются дифференциалами длин дуг соответствующих координатных линий.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Основные операции векторного анализа в криволинейных координатах

Дифференциальные уравнения векторных линий

Рассмотрим поле вектора

Уравнения векторных линий в криволинейных координатах q1,q2, q3 имеют вид

В цилиндрических координатах (q1 = р, q2= φ, q3 = z)
(1)

в сферических координатах (q1 = r, q2 = θ, q3 = φ)
(2)

Градиент в ортогональных координатах

Пусть и = u(q1, q2, q3) — скалярное пoле. Тогда

В цилиндрических координатах (q1 = р, q2 = φ, q3 = z)
(3)

в сферических координатах (q1 = r, q2 = θ, q3 = φ) (4)

Ротор в ортогональных координатах

Рассмотрим векторное поле

и вычислим rot а. Имеем

В цилиндрических координатах

в сферических координатах

Дивергенция в ортогональных координатах

Дивергенция div а векторного поля

вычисляется по формуле
(7)

В цилиндрических координатах

в цилиндрических координатах

в сферических координатах

Применяя формулу (7) к единичным векторам е1, е2, е3, получим

Вычисление потока в криволинейных координатах

Пусть S — часть координатной поверхности q1 = с = const, ограниченная координатными линиями

Тогда поток вектора

через поверхность S в направлении вектора e1 вычисляется по формуле
(8)

Аналогично вычисляется поток через часть поверхности q2 = с, а также через часть поверхности д3 = с, где с = const.

Пример:

Найти поток П векторного поля

через внешнюю сторону верхней полусферы S радиуса R с центром в начале координат.
Полусфера S есть часть координатной поверхности r = const, а именно r = R. На полусфере S имеем

Учитывая, что в сферических координатах

по формуле (8) найдем

Вычисление потенциала в криволинейных координатах

Пусть в некоторой области Ω задано потенциальное векторное поле

т. e. rot а = 0 в области Ω.

Для нахождения потенциала и = и(q1, q2, q3) этого векторного поля запишем равенство а(М) = grad u(M) в следующем виде:

Отсюда следует, что
(9)

Интегрируя систему дифференциальных уравнений с частными производными (9), найдем искомый потенциал

где с — произвольная постоянная.

В цилиндрических координатах

система (9) принимает вид

В сферических координатах

система (9) имеет вид

Пример:

Найти потенциал векторного поля, заданного в цилиндрических координатаx

Убедимся, что rot a = 0. По формуле (S) получим

т.е. данное поле потенциально.

Искомый потенциал u = и(р, φ, z) является решением следующей системы дифференциальных уравнений с частными производными (см. формулу (10)):

Интегрированием по р из первого уравнения находим

Дифференцируя соотношение (11) no φ и используя второе уравнение, получим

или 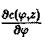= 0, откуда с = c1(z). Таким образом,

Дифференцируя это соотношение по z и используя третье уравнение, получим

или c1`(z) =0, откуда c1(z) = с. Итак, потенциал данного поля

Линейный интеграл и циркуляция в ортогональных криволинейных координатах

Пусть векторное поле

определено и непрерывно в области Ω изменения ортогональных криволинейных координат q1, q2, q3. Так как дифференциал радиус-вектора r любой точки M(q1, q2, q3) ∈ Ω выражается формулой

то криволинейный интеграл вектора а(М) по ориентированной гладкой или кусочно-гладкой кривой L ⊂ Ω будет равен
(13)

В частности, для цилиндрических координат (q1 = р, q2 = φ, q3 = z, Н1 = 1, Н2 = р, Н3=1) будем иметь

Отсюда по формуле (13) получим
(14)

Аналогично для сферических координат (q1 = r, q2 = θ, q3 = φ, Н1 = 1, Н2 = r, H3 = r sin θ будем иметь

Отсюда по формуле (13) получим
(15)

Если кривая L замкнута (начальная и конечная точки кривой L совпадают), то циркуляция Ц векторного поля а (М) в криволинейных координатах q1, q2, q3 вычисляется по формуле (13), а в случае цилиндрических или сферических координат — по формулам (14) или (15) соответственно.

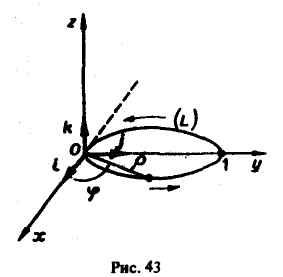
Пример:

Вычислить циркуляцию векторного поля, заданного в цилиндрических координатах

по замкнутой кривой L,

Координаты данного вектора равны соответственно

Контур L представляет собой замкнутую кривую, расположенную в плоскости z = 0 (рис. 43).

Подставляя координаты данного вектора в формулу .(14), получим

На кривой L имеем

Искомая циркуляция будет равна

Оператор Лапласа в ортогональных координатах

Используя формулы (16) и (17), для оператора Лапласа ∆ получим следующее выражение:

В цилиндрических координатах

В сферических координатах

Пример:

Найти все решения уравнения Лапласа ∆и = 0, зависящие только от расстояния r.

Так как искомое решение и должно зависеть только от расстояния точки М от начала координат г, т. е. и = и (r), то уравнение Лапласа ∆и = 0 в сферических координатах будет иметь вид

Отсюда 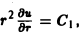так что

где С1 и С2 — постоянные.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:ГрадиентСкачать

5.6. Производная по направлению. Градиент. Линии уровня функции

Определение. Предел отношения 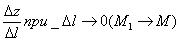, если он существует, называется Производной функции Z=F(M) в точке M(X; Y) по направлению вектора L .

Обозначение.

Если функция F(M) дифференцируема в точке М(х; у), то в точке М(х; у) существует производная по любому направлению L, исходящему из М; вычисляется она по следующей формуле:

(8)

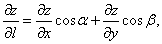
Где Cos И Cos — направляющие косинусы вектора L.

Пример 46. Вычислить производную функции Z=X2+Y2X в точке М(1; 2) по направлению вектора ММ1, где М1 – точка с координатами (3; 0).

Решение. Найдем единичный вектор L, имеющий данное направление:

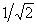
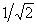
Откуда Cos=; Cos=-.

Вычислим частные производные функции в точке М(1; 2):

По формуле (8) получим

Пример 47. Найти производную функции U = Xy2Z3 в точке М(3; 2; 1) В направлении вектора MN, где N(5; 4; 2).

Решение. Найдем вектор 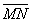и его направляющие косинусы:

Вычислим значения частных производных в точке М:

Следовательно,

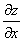
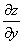
Определение. Градиентом Функции Z=F(M) в точке М(х; у) называется вектор, координаты которого равны соответствующим частным производным и, взятым в точке М(х; у).

Обозначение.

Решение. Находим частные производные: 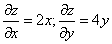и их значения в точке М(2; -1):

Пример 49. Найти величину и направление градиента функции 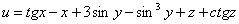в точке

Решение. Найдем частные производные и вычислим их значения в точке М:

Аналогично определяется производная по направлению для функции трех переменных U=F(X, Y, Z), выводятся формулы

Вводится понятие градиента

Подчеркнем, что Основные свойства градиента функции важнее для анализа экономических оптимизационных задач: в направлении градиента функция возрастает. В экономических задачах находят применение следующие свойства градиента:

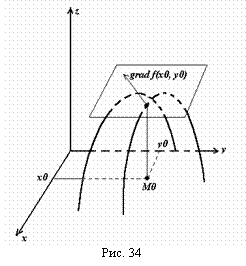
1) Пусть задана функция Z=F(X, Y), имеющая частные производные в области определения. Рассмотрим некоторую точку М0(х0, у0) из области определения. Значение функции в этой точке пусть равно F(X0, Y0). Рассмотрим график функции. Через точку (X0, Y0, F(X0, Y0)) трехмерного пространства проведем плоскость, касательную к поверхности графика функции. Тогда градиент функции, вычисленный в точке (х0, у0), рассматриваемый геометрически как вектор, приложенный в точке (X0, Y0, F(X0, Y0)), будет перпендикулярен касательной плоскости. Геометрическая иллюстрация приведена на рис. 34.

2) Градиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого возрастания функции в точке М0. Кроме того, любое направление, составляющее с градиентом острый угол, является направлением роста функции в точке М0. Другими словами, малое движение из точки (х0, у0) по направлению градиента функции в этой точке ведет к росту функции, причем в наибольшей степени.

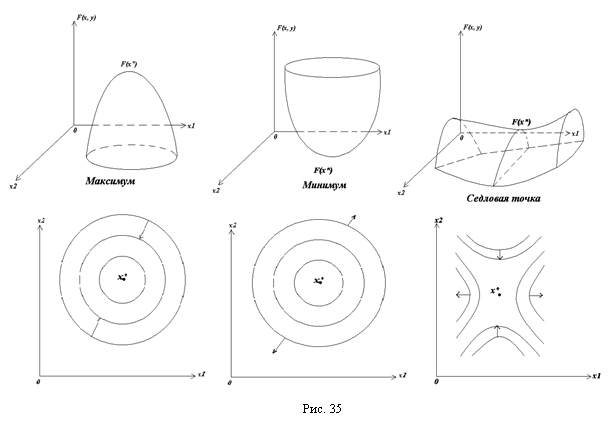
Рассмотрим вектор, противоположный градиенту. Он называется Антиградиентом. Координаты этого вектора равны:

Антиградиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого убывания функции в точке М0. Любое направление, образующее острый угол с антиградиентом, является направлением убывания функции в этой точке.

3) При исследовании функции часто возникает необходимость нахождения таких пар (х, у) из области определения функции, при которых функция принимает одинаковые значения. Рассмотрим множество точек (X, Y) из области определения функции F(X, Y), таких, что F(X, Y)=Const, где запись “Const” означает, что значение функции зафиксировано и равно некоторому числу из области значений функции.

Линии уровня геометрически изображаются на плоскости изменения независимых переменных в виде кривых линий. Получение линий уровня можно представить себе следующим образом. Рассмотрим множество С, которое состоит из точек трехмерного пространства с координатами (X, Y, F(X, Y)=Const), которые, с одной стороны, принадлежат графику функции Z=F(X, Y), с другой — лежат в плоскости, параллельной координатной плоскости ХОУ, и отстоящей от неё на величину, равную заданной константе. Тогда для построения линии уровня достаточно поверхность графика функции пересечь плоскостью Z=Const и линию пересечения спроектировать на плоскость ХОУ. Проведенное рассуждение является обоснованием возможности непосредственно строить линии уровня на плоскости ХОУ.

Определение. Множество линий уровня называют Картой линий уровня.

Хорошо известны примеры линий уровня – уровни одинаковых высот на топографической карте и линии одинакового барометрического давления на карте погоды.

Определение. Направление, вдоль которого скорость увеличения функции максимальна, называется «предпочтительным» направлением, или Направлением наискорейшего роста.

«Предпочтительное» направление задается вектором-градиентом функции. На рис. 35 изображены максимум, минимум и седловая точка в задаче оптимизации функции двух переменных при отсутствии ограничений. В нижней части рисунка изображены линии уровня и направления наискорейшего роста.

Решение. Уравнение семейства линий уровня имеет вид X2+Y2=C (C>0). Придавая С различные действительные значения, получим концентрические окружности с центром в начале координат.

Построение линий уровня. Их анализ находит широкое применение в экономических задачах микро — и макроуровня, теории равновесия и эффективных решений. Изокосты, изокванты, кривые безразличия – это все линии уровня, построенные для разных экономических функций.

Пример 51. Рассмотрим следующую экономическую ситуацию. Пусть производство продукции описывается Функцией Кобба-Дугласа F(X, Y)=10х1/3у2/3, где Х – количество труда, У – количество капитала. На приобретение ресурсов выделено 30 у. ед., цена труда составляет 5 у. ед., капитала – 10 у. ед. Зададимся вопросом: какой наибольший выпуск можно получить в данных условиях? Здесь под «данными условиями» имеются в виду заданные технологии, цены на ресурсы, вид производственной функции. Как уже отмечалось, функция Кобба-Дугласа является монотонно возрастающей по каждой переменной, т. е. увеличение каждого вида ресурса ведет к росту выпуска. В данных условиях ясно, что увеличивать приобретение ресурсов можно до тех пор, пока хватает денег. Наборы ресурсов, стоимость которых составляет 30 у. ед., удовлетворяют условию:

Т. е. определяют линию уровня функции:

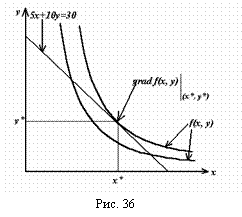
С другой стороны, с помощью линий уровня Функции Кобба-Дугласа (рис. 36) можно показать возрастание функции: в любой точке линии уровня направление градиента – это направление наибольшего возрастания, а для построения градиента в точке достаточно провести касательную к линии уровня в этой точке, построить перпендикуляр к касательной и указать направление градиента. Из рис. 36 видно, что движение линии уровня функции Кобба-Дугласа вдоль градиента следует производить до тех пор, пока она не станет касательной к линии уровня 5х + 10у = 30. Таким образом, с помощью понятий линии уровня, градиента, свойств градиента можно выработать подходы к наилучшему использованию ресурсов с точки зрения увеличения объемов выпускаемой продукции.

💡 Видео

Производная по направлениюСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Модуль вектора. Длина вектора.Скачать

ГРАДИЕНТ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХСкачать

Производная по направлениюСкачать

Производная по вектору и по направлению. Градиент. Примеры.Скачать

Производная по направлению. Градиент. Примеры.Скачать

Градиент. ТемаСкачать