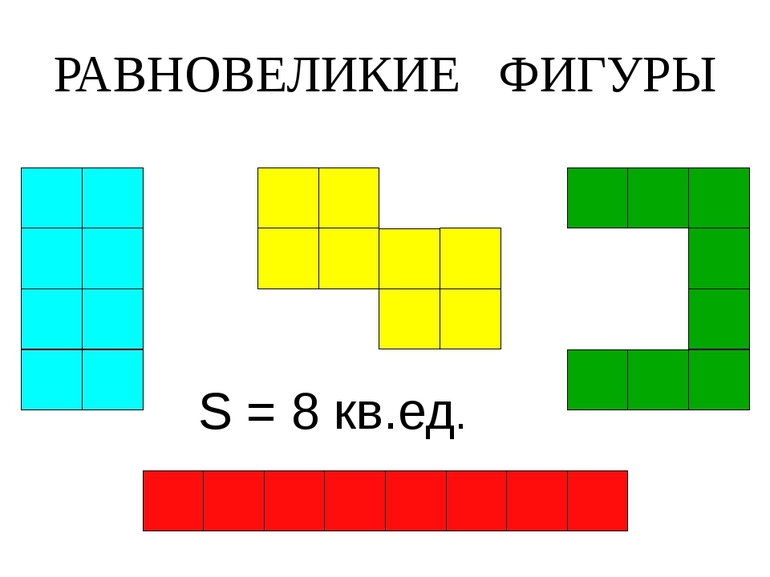
Равновеликие фигуры — это фигуры, которые имеют одинаковые площади.
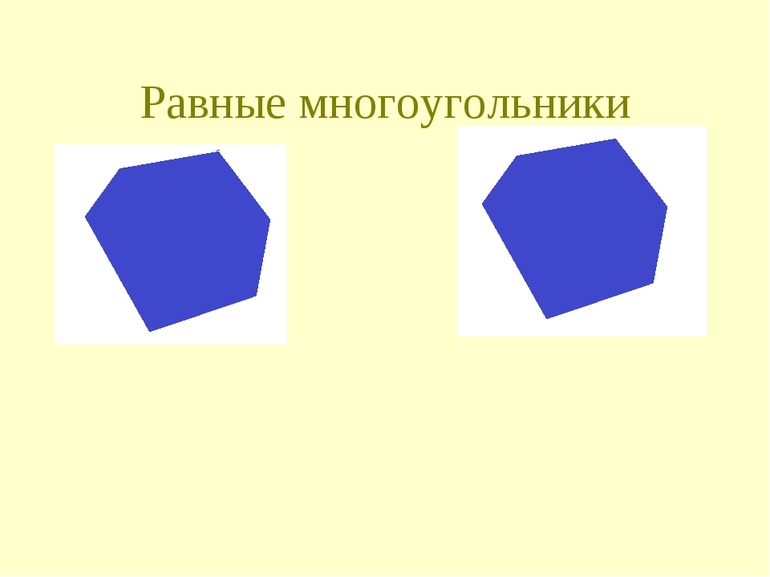
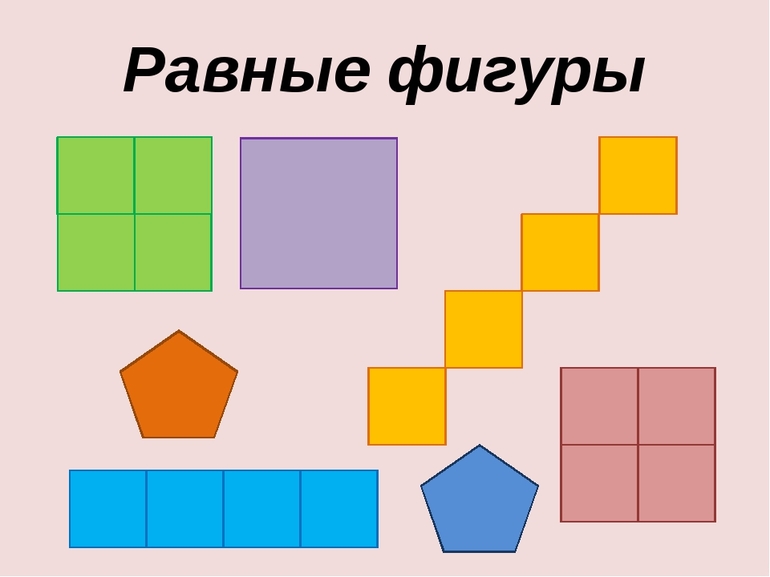
Равновеликие тела — это тела, которые имеют равные объёмы (равновеликие тела часто также называют равновеликими фигурами). Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).
Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.
Примеры равновеликих фигур .
1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.
То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если
2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.
Площадь квадрата S=3²=9.
Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если
3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.
Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если
Видео:Равновеликие треугольникиСкачать
Равновеликие фигуры — свойства, формулы и примеры
Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Равные многоугольники
По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:
- По трём сторонам.
- По стороне и двум прилегающим к ней углам.
- По двум сторонам и углу между ними.
Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.
Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».
В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.
Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.
Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Равность правильных фигур
Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».
Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.
Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.
Видео:Как выпуклый четырёхугольник разрезать по прямой, содержащей его вершину, на две равновеликие части?Скачать

Вычисление площади треугольника
Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.
Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.
- По двум сторонам и углу между ними.
- По стороне и высоте, проведённой к ней.
- По трём сторонам и полупериметру.
- По полупериметру и радиусу вписанной окружности.
- По трём сторонам и радиусу описанной окружности.
То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.
Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Визуальный способ
Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.
Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Равновеликие фигуры
Презентация к уроку
Загрузить презентацию (299 кБ)
Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Ход урока
I. Повторение.
1) Устно по готовому чертежу вывести формулу площади параллелограмма.
2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?
(по готовому чертежу)
зависимость обратно пропорциональная.
3) Найти вторую высоту (по готовому чертежу)
4) Найти площадь параллелограмма по готовому чертежу.
Решение:
5) Сравните площади параллелограммов S1, S2, S3. (Они имеют равные площади, у всех основание a и высота h).
Определение: Фигуры, имеющие равные площади, называются равновеликими.
II. Решение задач.
1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.
Решение:
2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.
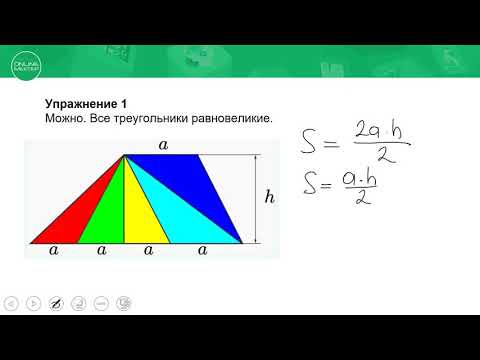
3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?
Решение: Можно. Все треугольники равновеликие.
4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.
Решение:
5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?
Решение: В точке пересечения диагоналей.
6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.
Решение:
III. Изучение темы «Площадь треугольника»
начать с задачи:
«Найти площадь треугольника, у которого основание a, а высота h».
Ребята, используя понятие равновеликих фигур, доказывают теорему.
Достроим треугольник до параллелограмма.
Площадь треугольника равна половине площади параллелограмма.
Задание: Начертите равновеликие треугольники.
Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).
Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».
У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь
Вывод: Фигуры, имеющие равные площади, называются равновеликими.
Вопросы к классу:
- Равновелики ли равные фигуры?
- Сформулируйте обратное утверждение. Верно ли оно?
- Верно ли:
а) Равносторонние треугольники равновелики?
б) Равносторонние треугольники с равными сторонами равновелики?
в) Квадраты с равными сторонами равновелики?
г) Докажите, что параллелограммы, образованные при пересечении двух полос одинаковой ширины под разными углами наклона друг к другу, равновелики. Найдите параллелограмм наименьшей площади, образующийся при пересечении двух полос одинаковой ширины. (Показать на модели: полоски одинаковой ширины)
IV. Шаг вперёд!
На доске написаны задания по выбору:
1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».
Решение:

2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».
Решение:
3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур 
Решение:
Ответ:
3. Из олимпиадных задач:
«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.
Решение: провести диагональ BD.
Упражнение №475.
«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».
Использовать теорему Фалеса (разделить АC на 3 равные части).
V. Задача дня.
Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).
«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».
Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.
Дополнительные задачи (из олимпиадных задач):
1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».
Решение:
Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S∆ABK = 2m, ∆BCM = ∆MDK, SABCD = S∆ABK = 2m.
2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».
Решение:
S∆BCD = S∆ABC, т.к. у них общее основание BC и одинаковая высота.
3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?
Решение:
В треугольнике МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,
Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.
4) Сцепленные параллелограммы.
2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.
Решение:

и
, значит,
Список использованной литературы:
- Учебник «Геометрия 7-9» (авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
- Олимпиадные задачи разных лет, в частности из учебного пособия «Лучшие задачи математических олимпиад» (составитель А.А. Корзняков, Пермь, «Книжный мир», 1996).
- Подборка задач, накопленных за много лет работы.
🔥 Видео
8 класс, 3 урок, ЧетырехугольникСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Миникурс по геометрии. ЧетырехугольникиСкачать

Запомни: все формулы для площади треугольникаСкачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать

ЧУДЕСА ТВОРЯТ СРЕДНИЕ ЛИНИИ! С ума можно сойти! Видишь ответ?Скачать

Вписанные четырехугольники. 9 класс.Скачать

Задание 26 Площадь четырехугольникаСкачать

Математика 3 класс. Равносоставленные и равновеликие фигурыСкачать
8 класс. Геометрия. Равновеликость и равносоставленность фигур. 15.05.2020.Скачать
Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать


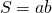
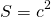
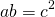

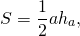
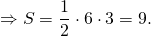
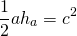

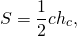
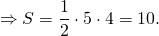
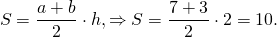












































 и
и  , значит,
, значит, 