Условия принадлежности 4 точек окружности доказательство

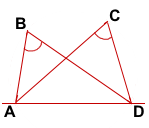
Признак принадлежности четырёх точек одной окружности

Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

Доказать: точки A, B, C, D лежат на одной окружности

Обозначим ∠ABD=∠ACD=α.

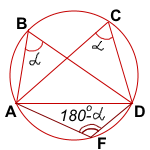
Опишем около треугольника ABD окружность.

Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.

Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:

Рассмотрим четырехугольник ACDF.

Отсюда следует, что четырёхугольник ABDF — вписанный.

Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.

Видео:ЕГЭ Задание 16 Условие принадлежности четырех точек окружностиСкачать

Презентация на тему «Признак принадлежности четырёх точек одной окружности»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Условие принадлежности четырёх точек одной окружностиСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описанная и вписанная окружности четырёхугольника Автор: учитель математики Румянцева Р.Г.

Признак принадлежности четырёх точек окружности

Признак принадлежности четырёх точек окружности Если точки А, М, N, В таковы что угол АМВ равен углу АNВ, причём точки M и N лежат в одной полуплоскости относительно прямой АВ, то точки А, М, N, В лежат на одной окружности.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 942 человека из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 315 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 694 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 479 939 материалов в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 10. Описанная и вписанная окружности четырёхугольника

Видео:Первое условие принадлежности четырех точек одной окружностиСкачать

Дистанционные курсы для педагогов

Другие материалы

• 25.11.2020
• 54

• 24.11.2020
• 138

• 24.11.2020
• 160

• 24.11.2020
• 158

• 24.11.2020
• 142

• 24.11.2020
• 270

• 24.11.2020
• 156

• 24.11.2020
• 88

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 25.11.2020 1024 —> —> —> —>
• PPTX 79.6 кбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Румянцева Рита Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На проекте: 5 лет и 1 месяц
• Подписчики: 0
• Всего просмотров: 2930
• Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Принадлежность четырех точек одной окружности. Попытка 2.Скачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В местах сдачи ЕГЭ будут применены антиковидные меры

Время чтения: 1 минута

Первые результаты по сокращению отчетности у учителей ожидаются осенью

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Первое условие принадлежности четырех точек окружностиСкачать

Применение комплексных чисел в элементарной геометрии

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Кафедра прикладной математики

«Применение комплексных чисел в элементарной геометрии»

Выполнила: студентка 2 курса

«Прикладная математика и

Научный руководитель: старший

§ 1. Параллельный перенос 4

§ 3. Подобие и движение 5

§ 4. Принадлежность трех точек прямой 7

§ 5. Принадлежность четырех точек окружности 8

§ 6. Ортоцентр треугольника 9

§ 7. Окружность и прямая Эйлера 10

§ 8. Прямая Симсона треугольника 12

Библиографический список 19

Большое значение комплексных чисел в математике и ее приложениях широко известно. Особенно часто применяются функции комплексного переменного. Вместе с тем алгебру комплексных чисел можно успешно использовать в элементарной геометрии, тригонометрии, теории геометрических преобразований, а также в электротехнике и различных задачах с механическим и физическим содержанием.

Метод комплексных чисел позволяет решать планиметрические задачи по готовым формулам прямым вычислением, элементарными выкладками. Выбор этих формул с очевидностью диктуется условиями задачи и ее требованием. В этом состоит простота данного метода, по сравнению с другими методами, ведь готовое решение может быть очень коротким.

В данной работе рассматривается применение комплексных чисел в планиметрии: описание преобразований плоскости, вывод некоторых формул для решения задач и доказательство некоторых свойств.

1. Описать параллельный перенос, вращение, движение первого и второго рода, подобие первого и второго рода с помощью операций над комплексными числами. Вывести условие принадлежности трех точек одной прямой и четырех точек одной окружности.

2. Доказать с помощью комплексных чисел свойства ортоцентра треугольника, существование окружности и прямой Эйлера.

3. Используя комплексные числа, доказать свойства прямой Симсона треугольника.

Работа состоит из введения, основной части, заключения и библиографического списка. Во введении кратко описывается значение выбранной темы, цель работы и структура работы. В основной части рассмотрены преобразования плоскости с помощью комплексных чисел, условия принадлежности точек прямой и окружности, свойства ортоцентра треугольника и прямой Симсона треугольника, а также доказательство существования окружности и прямой Эйлера и примеры решения задач с помощью комплексных чисел. В заключении представлены выводы о применении комплексных чисел в планиметрии.

Любое комплексное число можно единственным образом отобразить на плоскости как точку или радиус-вектор точки . Поэтому число называют точкой или вектором.

Зафиксируем два комплексных числа и . Найдем их сумму , которая означает, что , т.е. что вектор совпадает с вектором (геометрический смысл сложения комплексных чисел). Поэтому данное равенство определяет параллельный перенос плоскости на вектор .

Пусть даны точки , где , а arg ; , где , . Произведение двух комплексных чисел производится следующим образом:

где , а . Геометрически это обозначает, что точка , характеризующаяся модулем , является образом точки с модулем при композиции поворота с центром на угол =arg и гомотетии с центром и коэффициентом . Поскольку , точка будет также образом точки при композиции поворота с центром на угол , и гомотетии с центром и коэффициентом . Для построения точки удобно привлечь точку , которая равна единице. Имеем:

и ориентированные углы и равны ; следовательно, треугольники и подобны, что позволяет построить точку по точкам .

Таким образом умножение комплексных чисел определяет центрально-подобное вращение плоскости, составляющееся из вращения вокруг т. O на угол в положительном направлении (в направлении против часовой стрелки) и центрально-подобного преобразования с коэффициентом подобия t. Если модуль комплексного числа t=1, то данное преобразование представляет собой вращение на угол .

Любое движение плоскости можно представить или как вращение вокруг фиксированной точки O, сопровождаемое параллельным переносом, или как симметрию относительно фиксированной прямой o, сопровождаемую вращением вокруг выбранной точки O и параллельным переносом. Таким образом каждое движение плоскости можно представить в виде:

Подобие и движение

Преобразованием подобия (или подобием) называется преобразование, при котором каждые две точки отображены в такие две точки , что , где — постоянное действительное положительное число, называемое коэффициентом подобия. В частности, при расстояния равны, т. е. подобие является движением. Гомотетия с коэффициентом является подобием с коэффициентом

Фигура называется подобной фигуре , если существует подобие, отображающее . В частности, подобные треугольники являются соответственными при подобии. Преобразование, обратное подобию с коэффициентом , есть также подобие с коэффициентом . Существует два рода подобий плоскости. Подобие первого рода отображает каждый треугольник в одинаково ориентированный с ним (подобный) треугольник, а подобие второго рода меняет ориентацию каждого треугольника на противоположную.

Преобразование подобия плоскости задаётся тремя парами соответственных точек , заданных так, что треугольник подобен треугольнику . Однако если род подобия известен, то для его задания достаточно наличия двух пар соответственных точек.

По определению, треугольники называются подобными и одинаково ориентированными (подобие 1 рода) тогда и только тогда, когда (углы ориентированные). С помощью комплексных чисел эти равенства можно записать так:

где — комплексное число, – коэффициент подобия.

Составим формулы подобия первого и второго рода. При одинаковой ориентации треугольников имеем:

При противоположных ориентациях этих треугольников получим:

откуда

Итак, получены формулы для подобия первого и второго рода.

Проведем обратное рассуждение: пусть преобразование плоскости определено одной из формул

где и – постоянные комплексные числа, не может быть равна нулю. Тогда это преобразование первого или второго рода соответственно. Если точки переходят в точки , то при первом преобразовании
, а при втором Следовательно, в обоих случаях

Очевидно, если , то вышеприведенными формулами задаются движения плоскости первого и второго рода соответственно.

Принадлежность трех точек прямой

есть отношение трех точек . Угол между прямыми, пересекающимися в точке и проходящими через точки равен аргументу отношения :

есть ориентированный угол между ориентированными прямыми .

Условием того, что три точки лежат на одной прямой, является вещественность отношения этих трех точек или то, что угол или .

Т.к. три точки лежат на одной прямой, то они коллинеарны. Следовательно, по условию коллинеарности, отношение – действительное число.∎

Принадлежность четырех точек окружности

Условием того, что четыре точки лежат на одной окружности является то, что разность углов или , или вещественность их двойного отношения , т.е., аналогично условию принадлежности трех точек прямой, отношение

является двойным отношением четырех точек .

Если точки коллинеарны, то отношения – действительные числа (по критерию коллинеарности точек). Следовательно, в этом случае будет действительно и двойное отношение.

Если точки лежат на окружности, то рассмотрим два возможных случая:

1) точки находятся в одной полуплоскости относительно прямой ,

2) точки лежат в различных полуплоскостях относительно прямой .

В первом случае ориентированные углы равны, во втором случае , т.е. В обоих случаях разность или . Но т.к. эта разность равна

то w – действительное число.∎

Рассмотрим треугольник . Условимся, что , т.е. все вершины треугольника принадлежат единичной окружности (центр описанной окружности O — начало координат, а радиус — единица длины). Таким образом очевидно, что точка , которая равна есть вершина ромба , из чего следует, что прямые взаимно перпендикулярны как диагонали ромба; точка

является серединой стороны треугольника . Точка – вершина параллелограмма , т.е. , т.е. — высота треугольника , а – точка пересечения высоты со стороной . Аналогично можно доказать, что прямые и — высоты треугольника . Поэтому — точка пересечения высот треугольника, т.е. является ортоцентром.

Рассмотрим теперь некоторые свойства ортоцентра треугольника.
Из рисунка видно, что расстояние от ортоцентра треугольника до точки , симметричной центру описанной окружности относительно стороны , равно радиусу окружности , описанной вокруг треугольника . Аналогично для и , симметричных центру описанной окружности относительно сторон треугольника. Поэтому окружности , с центром в точках соответственно, равны окружности , и ортоцентр треугольника является точкой пересечения этих окружностей.

Также мы можем увидеть, что расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны треугольника. Возьмем отрезки и . Они равны, как противоположные стороны параллелограмма, а прямая является половиной отрезка (по свойствам ромба).

Окружность и прямая Эйлера

Рассмотрим точку

Очевидно, что это точка пересечения диагоналей параллелограмма , и через неё проходит средняя линия параллелограмма, причем

Таким образом, окружность с центром и радиусом проходит через точку — середину стороны — и через точку — середину отрезка . Аналогично можно доказать, что эта окружность проходит и через точки

двух других сторон и середины отрезков двух других высот. Окружность впервые была рассмотрена Леонардом Эйлером и называется окружностью Эйлера. Также её называют окружностью девяти точек треугольника, т.к. она проходит через девять замечательных точек: – середины сторон, — основания высот, — середины отрезков, соединяющих вершины треугольника с ортоцентром.

Прямая называется прямой Эйлера треугольника. Ей принадлежат центр O описанной окружности треугольника , точка

пересечения медиан, точка пересечения высот и центр

окружности Эйлера, причем

Прямая Симсона треугольника

Дана единичная окружность S плоскости комплексных чисел, описанная вокруг треугольника . Найдем основания перпендикуляров , опущенных из некоторой точки этой окружности на стороны . Основание перпендикуляра, опущенного из точки окружности на хорду выражается числом

т.к. является точкой пересечения перпендикулярных секущих к окружности.

Отсюда следует, что

Поскольку точки , , и принадлежат одной окружности S, то полученное двойное отношение вещественно, из этого следует, что вещественно и исходное отношение и следовательно, три точки принадлежат одной прямой. Эта прямая называется прямой Симсона (точки относительно треугольника ).

Выведем теперь уравнение прямой Симсона . Будем исходить из формы уравнения прямой, проходящей через точки :

нормируем это уравнение, поделив все его члены на коэффициент при :

Положив здесь , получим следующее выражение для коэффициента при :

(т.к. и аналогично для , и ). Чтобы определить свободный член C уравнения, достаточно подставить это уравнение

тогда

а т.к.

Получаем окончательное уравнение:

Очевидно, что точка

лежит на прямой Симсона. Если составить четырехугольник , где , то получим, что прямая Симсона вершины вписанного в окружность четырехугольника проходит через центр Z окружностиЭйлера этого четырехугольника.

Решим некоторые задачи методом комплексных чисел.

В результате поворота на вокруг точки отрезок перешёл в отрезок . Доказать, что медиана треугольника перпендикулярна прямой .

Пусть координаты равны соответственно . Тогда точки и будут иметь координаты , а середина отрезка — координату Находим:

число – чисто мнимое. На основании критерия перпендикулярности (отрезки и перпендикулярны тогда и только тогда, когда число является чисто мнимым), прямые перпендикулярны.

Из основания высоты треугольника опущены перпендикуляры на две стороны, не соответственные этой высоте. Доказать, что расстояние между основаниями этих перпендикуляров не зависит от выбора высоты треугольника.

Пусть дан треугольник , причём описанная около него окружность имеет уравнение . Если — высота треугольника, то

Комплексные координаты оснований перпендикуляров, опущенных из точки на соответственно, равны

Так как . Это выражение симметрично относительно , т.е. расстояние не зависит от выбора высоты треугольника.

На плоскости даны четыре окружности такие, что окружности пересекаются в точках , окружности пересекаются в точках , окружности — в точках и окружности — в точках . Доказать, что если точки лежат на одной окружности или прямой, то и точки также лежат на одной окружности или прямой.

Так как точки лежат на одно окружности, то вещественным будет выражение

Аналогично для остальных точек составим вещественные выражения

Поэтому, вещественным будет и выражение

Следовательно, из вещественности двойного отношения вытекает и вещественность двойного отношения .

Известно, сколь широко используются комплексные числа в математике и её приложениях. Особенно часто применяется функции комплексного переменного, в частности, аналитические функции.

Вместе с тем алгебру комплексных чисел можно успешно использовать и в более простых разделах математики – элементарной геометрии, тригонометрии, теории движений и подобий, аффинных и круговых преобразований, а также в электротехнике и в различных механических и физических задачах.

Названные выше разделы элементарной математики хорошо описываются с использованием комплексных чисел, однако в литературе

это отражено мало. На русском языке фактически отсутствуют руководства по элементарной геометрии и примыкающей к ней теории преобразований, в которых использовался бы алгебраический аппарат комплексных чисел.

В работе большое место занимает вывод формул для решения планиметрических задач с помощью комплексных чисел, а также рассмотрены основные свойства некоторых фигур планиметрии. Также приведенные в ней вычисления сопровождаются иллюстрациями, с помощью которых можно легко разобраться с рассмотренными формулами и полученными результатами. В конце работы разобраны решения трех задач с помощью комплексных чисел.

Данная работа может быть использована, как пособие для решения задач планиметрии с помощью приведенных здесь формул.

1. Маркушевич А. И. Комплексные числа и конформные отображения – М.: Государственное издательство технико-теоретической литературы, 1954. – 52 с.

2. Понарин Я. П. Алгебра комплексных чисел в геометрических задачах: Книга для учащихся математических классов школ, учителей и студентов педагогических вузов – М.: МЦНМО, 2004. — 160 с.

3. Швецов Д. От прямой Симсона до теоремы Дроз-Фарни, Квант. — №6, 2009. – с. 44-48

4. Яглом И. М. Геометрические преобразования. Линейные и круговые преобразования. — Государственное издательство технико-теоретической литературы, 1956. – 612 с.

5. Яглом И. М. Комплексные числа и их применение в геометрии – М.: Физматгиз, 1963. – 192 с.

📽️ Видео

Второе условие принадлежности четырех точек окружностиСкачать

ОКРУЖНОСТЬ (признак принадлежности четырех точек одной окружности) ЧАСТЬ 4Скачать

ОГЭ Задание 25 Условие принадлежности четырёх точек одной окружностиСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Определение принадлежности точки окружностиСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Доказать, что точки лежат на одной окружностиСкачать

ОГЭ Задание 25 Две окружностиСкачать

Геометрия Точки A, M, N, B таковы, что угол AMB = углу ANB, причем точки M и N лежат в однойСкачать

Принадлежность точки прямой, лучу, отрезкуСкачать

Доказать, что точки лежат в одной плоскости - bezbotvyСкачать

Доказать, что точки лежат на одной окружности Д301Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать