Вектор диполя магнитного поля (5 видео) | Курс школьной геометрии

Понятие о магнитном диполь-дипольном взаимодействии

К магнитному диполю относят небольшую петлю с током. Слово «небольшая» означает, что размеры витка с током немного меньше, чем геометрические величины, характеризующие размеры петли. Любая петля с током может создавать магнитное поле, которое можно уподобить электрическому при помощи электрического диполя. Магнитный диполь обладает магнитным моментом p m → и электрическим моментом диполя p e → = q l → .

Выражение I S → = p m → ( 1 ) получило название момента магнитного диполя.

По формуле ( 1 ) видно, что величина по модулю равняется произведению силы тока, протекающего в контуре, на площадь, охваченную им. Магнитный момент и положительная нормаль к поверхности S имеют одинаковое направление. Значение векторного потенциала магнитного диполя по формуле определено как:

A → r → = μ 0 4 π p m → × r → r 3 ( 2 ) .

Магнитное поле, создающее магнитный диполь, запишется:

B → = μ 0 4 π 3 p m → · r → r → r 5 — p m → r 3 ( 3 ) .

Если даны большие расстояния от диполя в любом направлении, то наблюдается пропорциональные r 3 убывание поля и рост площади витка.

Слово диполь в применении к токам запутывает, так как не имеет отдельных магнитных полюсов, соответствующих электрическим зарядам. Создание магнитного «дипольного» поля происходит за счет элементарной петли с током, а не при помощи двух зарядов.

Содержание

Взаимодействие магнитных диполей
Энергия диполь-дипольного взаимодействия
И элементы вектора геомагнитного поля
Поля элементарных излучателей. Ближняя и дальняя зоны
🔍 Видео

Видео:Лекция №8 "Электричество и магнетизм" (Попов П.В.): Магнитный дипольСкачать

Взаимодействие магнитных диполей

Из данного представления о магнитном диполе как о витке с током можно представить следующую схему взаимодействия магнитных диполей. Один из витков ( 1 ) тока создает магнитное поле, описываемое формулой ( 3 ) , другой ( 2 ) , находясь в нем, взаимодействует с полем. Если магнитный диполь создает поле, но оно не значится однородным, то B → ≠ c o n s t . Следовательно, действующая сила магнитного поля на виток с током не равняется нулю. Элемент контура ( 2 ) подвергается силе d F → , перпендикулярной к вектору индукции поля, B → , создающего диполь ( 1 ) , то есть к линии в месте пересечения ее с элементом витка d l → . Отсюда следует, что прилагаемые к разным элементам контура (магнитного диполя 2 ) силы имеют форму симметричного конусного веера. Направление их результирующей идет вдоль стороны возрастания магнитной индукции поля, это говорит о втягивании диполя к стороне более сильного поля.

При неизменной ориентации магнитного момента диполя ( 2 ) , постоянной по отношению к полю диполя ( 1 ) , легко находится количественное выражение для силы взаимодействия диполей. Зависимость потенциальной энергии механического взаимодействия диполей W p m от x (через B ) возможно по формуле:

F x = — ∂ W p m ∂ x = p m 2 ∂ B 1 ∂ x cos a ( 4 ) , где B 1 является индукцией поля, создаваемого магнитным диполем ( 1 ) , p m 2 – магнитным моментом диполя ( 2 ) , a – углом между вектором поля и вектором магнитного момента. Некоторые случаи говорят об слабом изменении поля при других направлениях:

F = F x = p m 2 ∂ B 1 ∂ x cos a ( 5 ) .

Из выражения ( 5 ) видно, что сила, действующая на магнитный диполь в поле другого диполя, находится в зависимости от взаимной ориентации магнитных моментов. Когда вектор p m 2 → ↑ ↑ B 1 → ( a = 0 ) , тогда значение силы взаимодействия диполей положительная и направлена в сторону возрастания B 1 → (считается, что ∂ B 1 ∂ x > 0 ), кроме силы F .

При действии на контур с током вращательного момента M → :

M → = p m 2 → B 1 → ( 6 ) .

Модуль вектора М запишется как:

M = p m 2 B sin a ( 7 ) .

Видео:Электродинамика | "магнитный диполь"Скачать

Энергия диполь-дипольного взаимодействия

Допустим, что два диполя обладают магнитными моментами p m i → , p m j → и располагаются в точках, определенных радиус-векторами r i → r j → . Тогда запись энергии их взаимодействия имеет вид:

W i j = — p m i → , B j → p m j → , r j → = — μ 0 4 π p m i → , 3 p m j → · r → r → r 5 — p m j → r 3 ( 8 ) .

Энергия диполь-дипольного взаимодействия зависит от взаимного расположения диполей.

Провести сравнение поля электрического диполя и поля магнитного диполя.

Формула напряженности поля электрического диполя записывается как:

E → = 1 4 πε 0 ε 3 p e → · r → r → r 5 — p e → r 3 ( 1 . 1 ) , где p e → = q l → является электрическим моментом диполя.

По выражению ( 1 . 1 ) наблюдается убывание напряженности поля диполя пропорционально третьей степени расстояния от диполя до точки, в которой рассматривается данное поле.

Создаваемое магнитным диполем магнитное поле запишется как:

B → = μ 0 4 π 3 p m → · r → r → r 5 — p m → r 3 ( 1 . 2 ) , p m → = I S → обозначает магнитный момент магнитного диполя.

Следуя из ( 1 . 1 ) , ( 1 . 2 ) , поведение магнитного и электрического полей аналогичное. Это способствовало тому, чтобы элементарный ток стали называть магнитным диполем. Их схожесть объясняется возникновением дипольных полей при нахождении наблюдателя далеко относительно токов и зарядов. Тогда в большей части пространства уравнения для напряженности электрического поля и индукции магнитного схожи по форме. Дивергенция и ротор у них равняются нулю. Это говорит о том, что решения будут аналогичными. Но источники, конфигурацию которых мы описываем при помощи дипольных моментов, физически сильно отличаются. В магнитном поле – это ток, в электрическом – заряды.

Показать, что энергия диполь-дипольного взаимодействия находится в зависимости от взаимной ориентации диполей.

Для решения необходимо применить формулу энергии магнитного взаимодействия полей, которая имеет вид:

W i j = — p m i → , B j → p m j → , r j → = — μ 0 4 π p m i → , 3 p m j → · r → r → r 5 — p m j → r 3 ( 2 . 1 ) .

Где p m i → , p m j → являются магнитными моментами диполей, r i → , r j → – радиус-векторами, определяющими положения диполей.

Произведем преобразование ( 2 . 1 ) , тогда:

W i j = μ 0 4 π p m j p m i r i j 2 — 3 r i j p m j r i j p m i r i j 5 = μ 0 4 π p m j p m j cos υ i j — 3 cos υ j cos υ i r i j 3 ( 2 . 2 ) , с r i j = r i — r j , υ i j , являющимся углом между векторами p m i → , p m j → .

Из ( 2 . 2 ) понятно, что энергия W i j находится в зависимости от взаимного расположения диполей. Для пары диполей с одинаковыми дипольными моментами p m j = p m i = p , с их горизонтальной параллельной ориентацией выявляется минимальность энергии взаимодействия диполей. Запишем в виде получившегося выражения:

Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

И элементы вектора геомагнитного поля

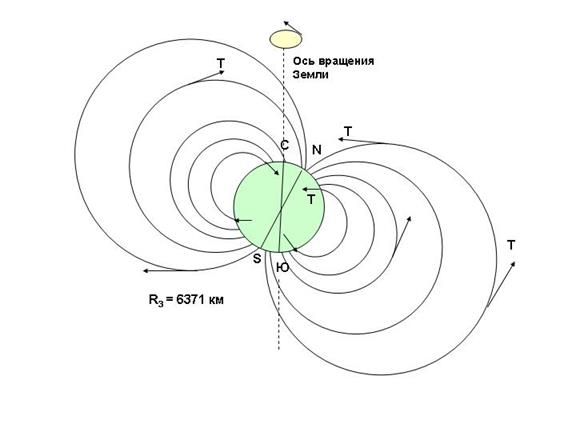
В первом приближении магнитное поле Земли подобно полю магнитного диполя (рис. 3.1), вектор магнитной индукции Т в точках магнитного экватора горизонтален, а на магнитных полюсах вертикален. На северном полюсе он направлен вниз, на южном — вверх. Модуль вектора увеличивается от экватора к каждому из полюсов примерно от 42 до 70 мкТл. Модуль соответствующего ему вектора напряженности магнитного поля Т изменяется от 33,4 до 55,7 А/м. Наилучшее совпадение поля диполя с фактическим наблюдается при условии, если магнитную ось диполя считать отклоненной от оси вращения Земли на 11,5°

Рис. 3.1. Магнитное поле Земли как поле диполя

Следует обратить внимание на то, что в северном полушарии, поскольку здесь вектор Т направлен вниз, расположен южный полюс диполя (по физической сущности у постоянных магнитов силу взаимного притяжения испытывают всегда разноименные полюсы). Несмотря на это, магнитный полюс северного полушария принято называть северным.

Из сказанного следует, что при переходе от одной точки поверхности Земли к другой вектор Т будет изменять и величину, и направление.

Если считать земное магнитное поле полем диполя, то для него потенциал определится по формуле:

Где М – магнитный момент Земли, равный 8,3 10 22 А*м2 или 8.3 10 25 ед. СГС, r – радиус Земли (6371 км), φ – магнитная широта.

Составляющие полного вектора индукции можно определить как производные по соответствующему направлению:

-(dU/dr) = Z = (2M/r 3 ) cos (90 – φ)

-(dU/rd(90 – φ)) = H = (M/r 3 )/sin(90 – φ). (3.2)

Полный вектор определится, как

T = (M/r 3 )[1+ 3cos2(90 – φ)] 1/2 , (3.3)

а магнитное наклонение

I 0 =arctg (Z/H) = 2 tgφ. (3.4)

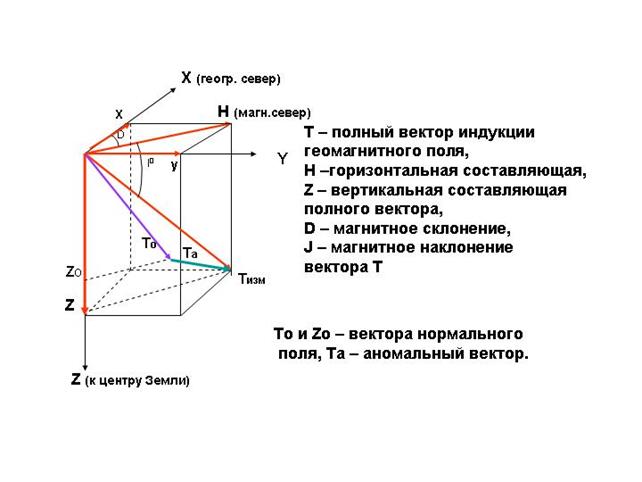
При изучении геомагнитного поля условились использовать единую систему прямоугольных координат Ох, Оу, Оz, у которой оси Ох и Оу горизонтальны (ось Ох направлена на север, ось Оу — на восток), а ось Оz — вертикальна (направлена вниз) (рис. 3.2).

Рис. 3.2. Элементы вектора геомагнитного поля

Полный вектор Т в большинстве точек земной поверхности не совпадает ни с одной из осей. Вертикальную плоскость, проходящую через вектор Т, называют плоскостью магнитного меридиана. Проекцию вектора Т на горизонтальную плоскость называют горизонтальной составляющей магнитной индукции и обозначают через Н. Очевидно, Н всегда располагается в плоскости магнитного меридиана. Иногда вместо Н рассматривают ее проекции на оси Ох и Оу, т.е. Н заменяют северной Х- и восточной Y- составляющими. Угол от географического меридиана до магнитного или от оси Ох до Н, отсчитанный по часовой стрелке, называют магнитным склонением или просто склонением и обозначают через D. Угол между вектором Т и Н — составляющей или угол наклона T к горизонту называют наклонением и обозначают через I. Эти составляющие и углы принято называть элементами земного магнетизма или элементами вектора геомагнитного поля.

Для полной характеристики поля достаточно знать три из них, например D, I,. и Н, или D, Н и Z, или X, У и Z. Часто измеряют D, I, и Н, по которым можно вычислить все другие элементы по формулам

Х=НсоsD, Y=НsinD, Z=HtgI, Т=Н/соsI (3.5)

В магниторазведке при решении некоторых задач оперируют вектором напряженности поля. Будем обозначать модули вектора магнитной индукции и его составляющих через Т, Z, Н, Х, Y, а модули элементов вектора напряженности геомагнитного поля и его составляющих через Т 0 , Z 0 , Н 0 , X 0 , Y 0 .

Единицы измерения магнитных величин

Величина	Ед. СИ	Ед. СГС	Связь
Магнитный потенциал	Ампер	Ед. СГС	1ед. СГС =10/4π А
Магнитная индукция	Тесла	Гаусс	1 Гс = 10 -4 Тл
Поток магнитной индукции	Вебер	Максвелл	1 Мкс = 10 -8 Вб
Напряженность поля	Ампер/метр	Эрстед	1 Э = 1000/4π А/м
Абсолютная магнитная проницаемость	Генри/метр	Ед. СГС	μ₀μ (СГС) = μ_А (СИ)
Магнитная восприимчивость	Ед. Си	Ед.СГС	1 ед. СГС = 4π ед. СИ
Магнитный момент	А/м 2	Ед. СГС	1 ед. СГС = 10 -3 А/м
Намагниченность	А/м	Ед. СГС	1 ед.СГС = 1000 А/м

Дата добавления: 2015-06-27 ; просмотров: 2357 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:ЧК_МИФ 3_2_3_3_(ЭД) МАГНИТНЫЙ ДИПОЛЬ В МАГНИТНОМ ПОЛЕ МАГНИТНОГО ДИПОЛЯСкачать

Поля элементарных излучателей. Ближняя и дальняя зоны

Характер электромагнитного поля в той или иной точке пространства существенно зависит от того, насколько близко или далеко от излучателя расположена рассматриваемая точка. В электродинамике и в теории антенн имеются соответствующие понятия — ближняя и дальняя зоны поля. Связано такое деление с тем, что отдельные компоненты поля имеют различную зависимость от расстояния.

Любой сложный излучатель можно представить как систему элементарных излучателей, электрических или магнитных. В качестве элементарных излучателей выступают:

— электрический диполь — идеализированная электронейтральная система, представляющая собой совокупность двух равных по абсолютной величине разноименных точечных зарядов, находящихся на некотором расстоянии друг от друга;
— магнитный диполь — идеализированная магнитонейтральная система, моделируемая по причине отсутствия в природе магнитных зарядов в виде небольшой (по сравнению с расстояниями, на которых излучается генерируемое диполем магнитное поле) плоской замкнутой проводящей рамки с током.

Рассмотрим поле излучение элементарного электрического диполя. Для этого возьмем проводник очень малой длины / по сравнению с длиной волны Я, т.е. I « Я. Пусть ток, протекающий по проводнику, изменяется по гармоническому закону: / = l_m cos cot, причем ввиду малости длины проводника амплитуду тока можно считать постоянной (стационарной) по всей длине проводника, т.е. /_т = 1_ст. Это означает, что изменение значения тока происходит лишь на концах проводника: от нуля до /,„, и, наоборот, от 1_т до нуля. Тогда, согласно закону сохранения заряда, в этих точках должны существовать сосредоточенные колеблющиеся электрические заряды, равные по абсолютной величине и противоположные по зна К У : q = q„,smcot, q_m=I_mlco. Таким образом, мы имеем дело с электрическим диполем, совершающим гармонические колебания.

Опираясь на уравнения Максвелла, можно определить компоненты поля, создаваемого элементарным электрическим излучателем, в произвольной точке пространства. Анализ поля излучения элементарного электрического излучателя обычно выполняют в сферической системе координат, в центр которой помещен излучатель (рис. 3.26).

Электрический диполь длиной / с однородным током / создает сферическое поле. Возьмем поле произвольную точку М с координатами г — радиус-вектор, ср- азимутальный угол и в- полярный угол. При этом рассматриваемое расстояние значительно превышает размер диполя: г » I.

Рисунок 3.26 — Элементарный электрический излучатель в сферической системе координат

Проекции напряженностей электрического и магнитного полей в точке Мопределяются соотношениями:

где к = — — волновое число.

Из формул (3.124) следует, что каждая компонента поля (Е_г, Е₀, и Н _{2 г 2 и 1/кг. В результате получим только две отличные от нуля составляющие поля:}

где — Z₀ = Е_т/H_m = J/Ifs волновое сопротивление неограниченной среды (для вакуума Z₀ = Jpjel = 120л Ом или примерно 377 Ом).

Система уравнений (3.127) соответствуют полю излучения, представляющего собой сферическую волну. Векторы ? и Я расположены перпендикулярно к направлению распространения волны, взаимно перпендикулярны и находятся в одной фазе.

Вектор Умова-Пойтинга в дальней зоне имеет только одну радиальную составляющую:

причем ее мгновенное значение всегда оказывается положительным вследствие того, что векторы поля имеют одинаковую фазу колебаний. Это означает, что энергия движется в направлении радиусов только от излучателя (рис. 3.26). Она не возвращается обратно к излучателю и представляет собой энергию излученной электромагнитной волны. Максимальное излучение максимально в экваториальной плоскости 0 = л/2 и отсутствует в осевом направлении 0 = 0.

В ряде случаев между ближней и дальней зоной вводят еще одну зону. Под промежуточной зоной поля излучения понимается область пространства вокруг излучателя, характеризуемая расстояниями, соизмеримыми с длиной излучаемой волны. Тогда ни одним слагаемым в системе уравнений (3.124) пренебречь нельзя.

Теперь рассмотрим особенности поля излучения элементарного магнитного диполя. Простейшей физически осуществимой моделью элементарного магнитного излучателя является плоская проводящая рамка (одиночный виток провода) площадью S, по которой течет переменный ток I = I _т cos cot и периметр которой весьма мал по сравнению с длиной создаваемого ею поля. Такой виток (рамку) с переменным током называют элементарным магнитным излучателем, или магнитным диполем Герца, создающим такое же магнитное поле, как если бы на его месте находился абстрактный (воображаемый) элементарный магнитный диполь, ориентированный перпендикулярно плоскости рамки. Следовательно, при расположении магнитного диполя в центре сферической системы координат вдоль оси г элементарная электрическая рамка должна лежать в экваториальной ПЛОСКОСТИ 0 = 71/2.

Поле элементарного магнитного излучателя также имеет характер сферической волны достаточно сложного строения. Поле отличается только тем, что теперь электрические силовые линии представляют собой концентрические окружности вокруг оси z, а магнитные силовые линии лежат в меридиональных областях.

Из выражения (3.129) известным способом получаем компоненты ближнего поля:

а также поля излучения (дальней зоны):

Итак, в дальней зоне элементарный магнитный излучатель создает волновое поле, отличающееся от поля элементарного электрического излучателя только ориентацией векторов напряженностей ? и Я.

Поле любого сложного электрического излучателя может быть представлено как суперпозиция полей, создаваемых отдельными его элементами, принимаемыми за электрические или магнитные диполи. Рассчитывается это сложное поле для любой точки наблюдения с помощью приведенных здесь выражений это сложное поле возможно рассчитать. Принцип суперпозиции в таком контексте справедлив как для сложных электрических, так и магнитных излучателей.

Для защиты информации от утечки за счет электромагнитных излучений способом экранирования необходимо иметь четко сформулированные критерии деления пространства на зоны (области).

Наиболее простым является деление пространства на две части исходя из условия, что в некоторой точке пространства совпадают значения составляющих, определяемых слагаемыми, пропорциональными первой и второй степени 1 /г, т.е. формула критерия равна:

Этим расстоянием от источника поля все пространство делится на две области: ближнюю и дальнюю. Этот критерий используется наиболее часто. Однако при таком выборе границы областей ее положение будет изменяться в зависимости от частоты сигнала, излучаемого диполем или антенной.

Согласно другому критерию границу зон определяют исходя из изменений волнового импеданса. Этот критерий особенно важен при проектировании систем экранирования и защиты от электромагнитных излучений, если параметры излучения источника и расстояние до него точно известны. И этот критерий важен также для проектировщиков антенных систем, когда необходимо знать, как спадает поле при удалении от антенны.

Границей областей при волновом критерии принято считать расстояние, на котором волновое сопротивление перестает меняться и становится постоянным и равным волновому сопротивлению вакуума Z₀ = 120л: (377 Ом). Поскольку отношение импеданса экрана к импедансу падающей волны определяет эффективность системы экранирования, при ее проектировании знание сопротивления падающей волны очень важно.

Импеданс падающей волны определяется как отношение напряженности электрического поля, создаваемого излучателем в данной точке, к напряженности магнитного поля в той же точке. В этом случае критерий можно записать более точно, поделив все пространство на три зоны с двумя границами. Тогда для ближней области граница дается примерным соотношением

Для промежуточной (переходной) области соотношение для границы имеет вид

И для дальней области граница задается соотношением

В результате волновое пространство делится на три зоны:

1) Ближняя зона, называемая реактивной, поскольку поле имеет реактивной характер, так как переноса энергии практически не происходит и излучение отсутствует. Это означает, что в ближней зоне поля, запасающие энергию, преобладают над излучающими полями.
2) Промежуточная зона, называемая областью излучения ближнего поля или зоной дифракции Френеля.
3) Дальняя зона, называемая волновой областью или по-другому зоной Фраунгофера.

Зависимость волнового сопротивления от расстояния для различных критериев деления пространства на зоны представлена на рис. 3.27.

Итак, вдали от источника, изменяющегося во времени электромагнитного поля, отношение амплитуд электрических и магнитных полей равно 377 Ом. Вблизи от источника полей это отношение может быть совершенно другим, и будет зависеть от характера источника. Ближняя область составляет приблизительно около длины волны источника. При частоте 1 МГц это — приблизительно 45,7 м, и при 10 МГц — примерно 4,57 м. Знать размеры ближней зоны необходимо потому, что электромагнитные излучения в ней могут определяться либо электрическим полем, либо

магнитным полем. От характера основного поля несанкционированного побочного излучения зависит выбор системы экранирования и, следовательно, эффективность защиты информации.

Рисунок 3.27 — Зависимость волнового сопротивления от расстояния

В заключение данного параграфа следует отметить, что существование электрических, магнитных и электромагнитных полей в пространстве вокруг радиоэлектронных технических средств и систем есть объективная реальность. Поля, с одной стороны, выступая в качестве физического носителя информации, а, с другой стороны, воздействую на окружающие физические объекты, способствуют образованию каналов утечки информации. Поэтому для защиты информации необходимо решать задачу по ограждению физических тел от воздействия на них электрических, магнитных и электромагнитных полей.