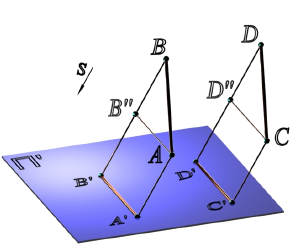
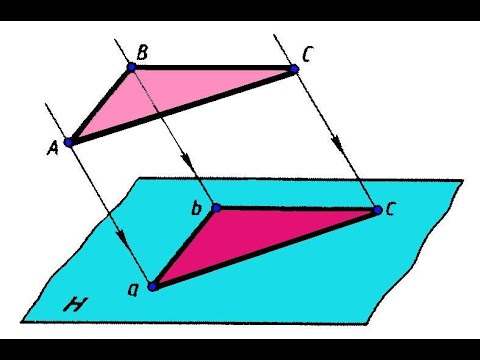
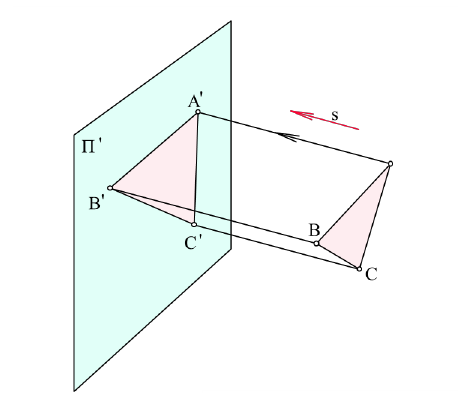
Геометрические фигуры проецируются на плоскость проекции, в общем случае, с искажениями. Причем характер искажений проекций по сравнению с оригиналом зависит от аппарата проецирования и положения проецируемой фигуры по отношению к плоскости проекции. В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин). Действительно, пусть дана прямоугольная трапеция ABCD. Плоскость трапеции не параллельна плоскости проекции α. Определим параллельную проекцию при заданном направлении проецирования s.
Из рисунка видно, что проекция ABCD Существенно отличается от оригинала ABCD. Изменились длины сторон трапеции, другими стали величины углов при ее вершинах. При таких условиях, естественно, нарушается равенство площадей фигуры оригинала и ее проекции.
Наряду с этим, между оригиналом и его проекцией существует определенная связь, заключающаяся в том, что некоторые свойства оригинала сохраняются и на его проекции. Такие свойства принято называть проективными или инвариантными (независимыми) для данного способа проецирования.
Основу любой геометрии составляет система аксиом. Любые геометрические определения и предложения, равно как и доказательства теорем, базируются на принятой системе аксиом. В процессе параллельного проецирования (получения проекций геометрической фигуры по ее оригиналу) или реконструкции чертежа (воспроизведение оригинала по заданным его проекциям), любое определение, любую теорему можно составить и доказать, опираясь на инвариантные свойства параллельного проецирования, которые играют в начертательной геометрии такую же важную роль, как аксиомы в геометрии.
Таким образом, можно утверждать, что в начертательной геометрии существует, как бы, две системы аксиом: — первая используется в процессе построения проекции геометрической фигуры по ее оригиналу. На этом этапе функции аксиом выполняют инвариантные свойства параллельного проецирования; После того, как проекции определены, можно рассматривать задачу как плоскую, вступает в силу вторая система — аксиоматика евклидовой геометрии.
Основные инвариантные свойства параллельного проецирования:
1. Проекция точки есть точка.
Это очевидно из самого определения проекции как точки пересечения проецирующего луча с плоскостью проекций.
2. Проекция прямой на плоскость есть прямая.
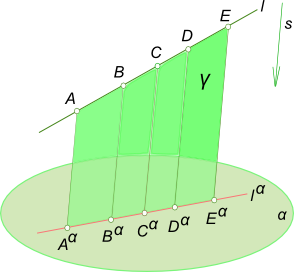
Действительно, при параллельном проецировании все лучи, проецирующие точки A,B,C,D,E прямой l, принадлежат одной плоскости Υ, параллельной направлению проецирования s. Эта плоскость пересекает плоскость проекции по прямой l α . (Исходя из этого справедливо и следующее утверждение. Прямая может быть проекцией не только прямой, но и любой кривой линии, если эта кривая находится в плоскости, перпендикулярной плоскости проекций.)
3. Если в пространстве точка принадлежит (инцидентна) линии, то проекция этой точки принадлежит проекции линии. Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.
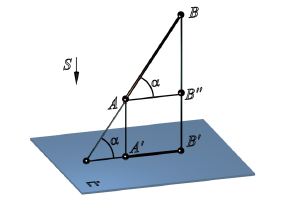
4. Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.
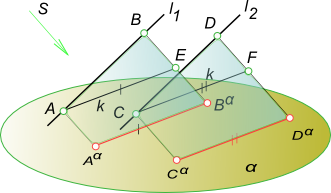
Если [AB]║[CD], то плоскости ABB α A α и CDD α C α параллельны как имеющие углы при вершинах B и D с соответственно параллельными сторонами — (BA)║(DC) и (BB α )║(DD α ). Эти плоскости пересекаются плоскостью проекции α по параллельным прямым l α 1║l α 2. Проведем в проецирующей плоскости ABB α A α через точку A прямую k1║l1, а в плоскости CDD α C α прямую k2║l2. Эти прямые пересекут проецирующие лучи [BB α ) и [DD α ) в точках E и F. Отрезок [AE] [A α B α ], а [CF] [C α F α ] как отрезки параллельных между параллельными. ΔABE подобен ΔCDF. На основании подобия треугольников можно записать:
Из четвертого свойства следует:
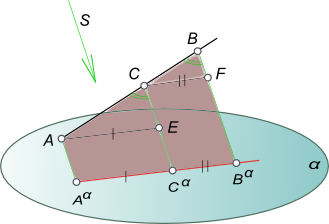
а) если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией этой точки в том же отношении.
Доказательство этого свойства аналогично предыдущему, понятно из чертежа на рисунке и не требует дополнительных пояснений.
Как следствие пункт a) можно записать: середина отрезка оригинала проецируется в середину его проекции. Поэтому медианы треугольника проецируются в медианы его проекций, а следовательно, центр тяжести треугольной пластинки проецируется в центр тяжести треугольника — проекций; центр окружности, как точка, делящая все диаметры пополам, проецируется в центр эллипса. Взаимно перпендикулярные диаметры окружности проецируются в сопряженные диаметры эллипса.
б) Проекции конгруентных отрезков взаимно параллельных прямых взаимно параллельны и конгруэнтны.
Поэтому проекцией любого параллелограмма будет параллелограмм. В параллелограммы проецируется также произвольно расположенный по отношению к плоскости проекции прямоугольник, ромб, квадрат.
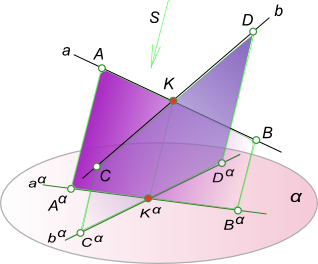
5. Точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих прямых. Пусть две прямые a и b пересекаются в точке K. Так как точка K принадлежит прямой a, то на основании свойства 3 K α ∈ a α . Одновременно K ∈ b, следовательно, K α ∈ b α . Эти два условия могут быть удовлетворены только в том случае, если K α будет точкой пересечения проекций прямых a и b.
6. Плоская фигура, параллельная плоскости проекции, проецируется на эту плоскость в конгруентную фигуру.
7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
Следствием этого свойства будут: — плоская ломанная линия проецируется, в общем случае, в ломанную линию с тем же числом вершин; — плоская кривая проецируется, в общем случае, в кривую линию; — проекция в виде отрезка прямой не определяет оригинала, которым могут быть: прямая, плоская ломанная или кривая линии, любая плоская фигура.
8. Параллельный перенос оригинала или плоскости проекции не изменяет вида и размеров проекции оригинала.
- Методы проецирования в начертательной геометрии с примерами
- Методы проецирования
- Центральное проецирование
- Параллельное проецирование
- Проецирование на плоскости координат
- Аксонометрические проекции
- Свойства прямоугольного проецирования
- Комплексный чертёж точки (эпюр точки)
- Центральный метод проецирования
- Параллельный метод проецирования
- Свойства параллельных проекций
- Ортогональные проекции
- Лекция 1. Методы проецирования
- 1.1. Центральное проецирование
- 1.2. Параллельное проецирование
- 1.3. Ортогональное проецирование. Метод Монжа
- 1.4. Прямоугольные проекции точки. Свойства ортогонального чертежа
- Упражнение
- 1.5. Задачи для самостоятельного решения
- 🌟 Видео
Видео:Начертательная геометрия. Методы проецированияСкачать

Методы проецирования в начертательной геометрии с примерами
Содержание:
Правила начертательной геометрии предусматривают построение изображений плоских или объёмных предметов с помощью приёма, называемого проецированием.
В начертательной геометрии для решения геометрических задач используется графический способ, при котором геометрические свойства предметов изучаются непосредственно по чертежу’. Для того, чтобы чертеж соответствовал изображаемому предмету, он должен быть построен по определенным геометрическим законам. Правила построения изображений в начертательной геометрии основаны на методе проекции. Метод проекций предполагает наличие плоскости проекций, объекта проецирования и проецирующих лучей.
Принятые обозначения:
Обозначения геометрических фигур
1. Точки, расположенные в пространстве, обозначаются прописными буквами латинского алфавита
2. Последовательность точек (и других элементов) — подстрочными индексами:
3. Линии в пространстве — по точкам, определяющим линию или строчными буквами латинского алфавита:
4. Углы — строчными буквами греческого алфавита
5. Плоскости — строчными буквами греческого алфавита
6. Поверхности — римскими цифрами 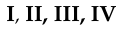
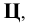
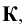
7. Плоскости проекций — строчной буквой греческого алфавита 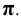
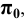
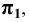
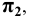
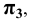
8. Оси проекций — строчными буквами 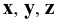
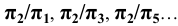
9. Проекции точек:
- на произвольную плоскость
- на горизонтальную плоскость
- на фронтальную плоскость
- на профильную плоскость
- на дополнительную плоскость
10. Проекции линий — по проекциям точек, определяющих линию; кроме того:
- горизонтальная линия — буквой
- фронтальная линия — буквой
- профильная линия — буквой
11. Обозначение плоскостей, заданных следами:
- горизонтальный след плоскости
- фронтальный след плоскости
- профильный след плоскости
В тех случаях, когда плоскость не требует наименования, обозначение следов упрощенно —
Для проецирующих плоскостей задаётся проекция плоскости:
— горизонтально — проецирующая плоскость
— фронтально — проецирующая плоскость
— профильно — проецирующая плоскость
Точки схода следов плоскости — прописными буквами X, Y, Z с индексом соответствующей плоскости: Xtt, Ya, Ztt.
12. При преобразовании эпюра (чертежа) вращением (или совмещением) в новом положении:
- точки —
- плоскости —
- следы плоскости —
После второго вращения соответственно:
Новое положение точки схода следов при вращении плоскости
Обозначения отношений между геометрическими элементами
1. Совпадение
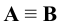
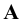
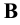
2. Параллельность ( 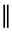
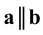
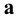
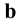
3. Перпендикулярность
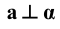
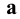
1. Принадлежность ( 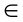
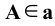
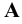
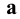
2. Включение (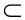
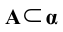
3. Пересечение ( 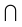
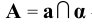
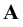
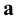
4. Импликация — логическое следствие
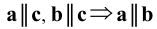
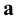
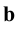
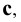
Видео:Параллельность прямой к плоскостиСкачать

Методы проецирования
Методы проецирования — это правила построения изображений, рассматриваемых в начертательной геометрии и применяемые в техническом черчении.
Изображение на плоскости предмета, расположенного в пространстве, полученное при помощи прямых линий — лучей, проведенных через каждую характерную точку предмета до пересечения этих лучей с плоскостью, называется проекцией этого предмета на данную плоскость.
Различают два метода проецирования: центральное и параллельное.
Центральное проецирование
Предположим, что в пространстве заданы (Рис. 1.1) кривая 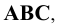
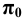
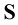
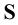
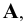
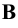
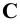
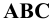
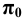
Обозначим полученные точки соответственно буквами 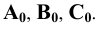
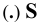
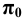
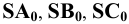
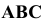
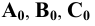
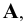
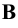
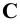
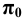
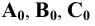
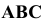
Центральное проецирование — это проецирование на заданную плоскость из заданного полюса (центра) проецирования.
Основные свойства центрального проецирования:
- любой геометрический элемент имеет на плоскости проекций единственную проекцию;
- любая точка на плоскости проекций является проекцией бесчисленного множества точек (любой точки, расположенной на проецирующем луче);
- проекцией прямой линии является прямая линия.
Достоинством центрального проецирования является наглядность изображения.
Недостаток — сложность определения истинных размеров оригинала по его изображению. Это ограничивает применение центрального проецирования, так как в технике определение истинных размеров проецируемого предмета по его изображению является одним из основных требований.
Данный метод, называемый перспективой, применяется в живописи, архитектуре. Кроме того, фотографии и киноизображения также являются центральными проекциями.
Дополнительное объяснение центрального проецирования:
Аппарат проецирования включает в себя проецирующие лучи, проецируемый объект и плоскость, на которой получается изображение оригинала.
Изображение точки 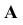
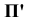
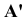
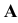
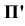
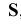
Рисунок 1.1 — Центральное проецирование
Центральное проецирование обладает наглядностью, оно используется при построении изображений архитектурно-строительных объектов, но дает значительное искажение размеров, вследствие чего не применяется для выполнения чертежей.
Подробное объяснение центрального проецирования:
Задается плоскость проекций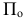
Проведем из S через А прямую до пересечения с плоскостью 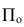
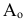
- S — центр или полюс проецирования /а
— плоскость проекций
— проецирующий луч (проецирующая прямая)
— центральная проекция точки А на плоскость
1 свойство: при заданных плоскости проекций и центре проёцирования одна точка в пространстве имеет одну центральную проекцию.
Но если есть проекция точки, S и П, то точку в пространстве найти нельзя.
2 свойство: каждая точка на плоскости проекций может быть проекцией бесконечного множества точек.
Центральным проецированием может быть построена проекция любой линии или поверхности как множество проекций всех её точек.
Центральные проекции линии не определяют проецируемую линию.
Для построения проекций линий, поверхностей или тел часто достаточно построить проекции лишь некоторых характерных точек.
ПРИМЕР: При построении на 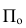

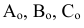
Центральное проецирование применяют для изображения предметов в перспективе, но для технического черчения этот метод неудобен.
Параллельное проецирование
Параллельное проецирование — проецирование с помощью параллельных проецирующих лучей, что наблюдается при бесконечном удалении полюса от плоскости проекций.
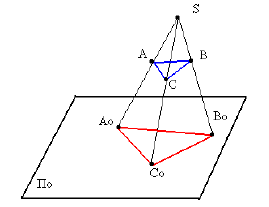
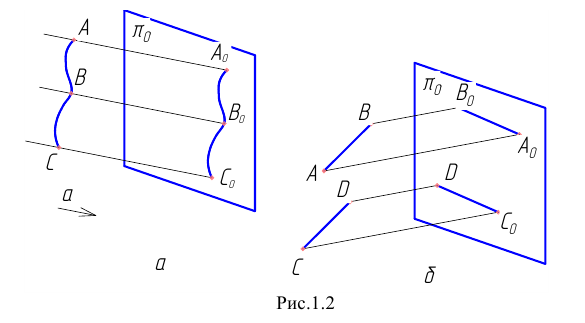
Пусть (Рис. 1.2, а) требуется построить изображение кривой 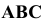
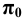
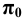
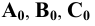
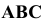
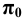
Параллельное проецирование обладает теми же свойствами, что и центральное. Кроме того, параллельные прямые проецируются в виде параллельных прямых (см. Рис. 1.2, б); отношение отрезков двух параллельных прямых 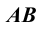
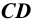
Параллельное проецирование разделяется на косоугольное и прямоугольное.
Косоугольное проецирование — это проецирование с помощью лучей, наклонённых к плоскости проекций под некоторым отличным от прямого углом.
Прямоугольное (ортогональное) проецирование — это проецирование с помощью лучей, перпендикулярных к плоскости проекций.
Плоскость проекций обычно относят к декартовой системе координат. Так, прямоугольное проецирование на горизонтальную и вертикальную плоскости проекций получило наименование «Метод прямоугольного проецирования на плоскости координат» (метод Г. Монжа).
Метод прямоугольного проецирования положен в основу выполнения технических чертежей.
Дополнительное объяснение параллельного проецирования:
При параллельном проецировании проецирующие лучи параллельны заданному направлению 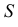
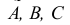
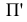
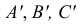
Параллельное проецирование можно рассматривать как частный случай центральною при бесконечно удаленном центре проекций В зависимости от направления проецирующих лучей относительно плоскости проекций параллельное проецирование может быть прямоугольным (проецирующие лучи перпендикулярны плоскости проекций) и косоугольным (проецирующие лучи составляют с плоскостью проекций угол, не равный 90°).
Если центр проекций удален в бесконечность, то все проецирующие лучи становятся параллельными и проецирование называется параллельным. В этом случае задается направление проецирования 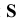
Ортогональное (прямоугольное) проецирование есть частный случай параллельного проецирования, когда все проецирующие лучи перпендикулярны к плоскости проекций 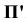
Ортогональная проекция получила наибольшее распространение в технических чертежах. Чертежи, полученные рассмотренными методами проецирования, не обладают свойством обратимости, т.е. по данному чертежу воспроизвести оригинал не решается однозначно.
Рисунок 1.2 — Параллельное проецирование
Подробное объяснение параллельного проецирования:
Его можно рассматривать как частный случай центрального, при котором центр проецирования удален в бесконечность.
Применяют параллельные проецирующие прямые, проведенные в заданном направлении.
Если направление проецирования перпендикулярно плоскости проекций, то проецирование называют прямоугольным или ортогональным.
При параллельном проецировании сохраняются все свойства центрального, а так же возникают следующие свойства:
- а) Проекции взаимно // прямых //, а отношение длин отрезков таких прямых равно отношению длин их проекций
- б) Плоская фигура, // плоскости проекций проецируется на эту плоскость в натуральную величину
- в) Если прямая перпендикулярна направлению проецирования, то её проекци ей является точка
Если есть центр параллельной проекции, мы не сможем определить положение точки в пространстве.
Гаспар Монж предложил взять две взаимно перпендикулярные плоскости проекций (горизонтальную 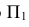
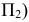
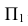
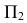
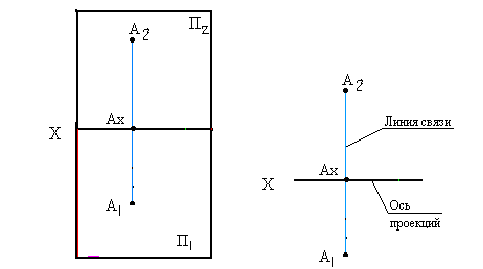
Ах А] и АхА2- перпендикулярны оси X -линии связи
Если есть в пространстве точка А, то опускаем из неё перпендикуляр на 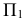
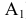
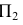
Но данное наглядное изображение точки в системе 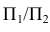
Преобразуем его так, чтобы горизонтальная плоскость проекций совпала с фронтальной, образуя одну плоскость чертежа.
Это преобразование осуществляется путем поворота вокруг оси X плоскости П| на угол 90° вниз. При этом 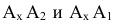
Получили чертеж под названием эпюр Монжа.
Горизонтальная и фронтальная проекции всегда лежат на одной линии связи у перпендикулярной оси.
В зависимости от сложности для полного выявления форм деталей бывает необходимо три и более изображений. Поэтому вводят три и более плоскостей проекций.
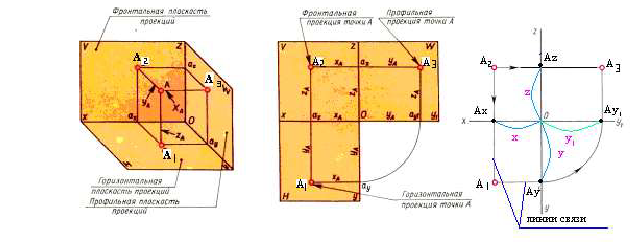
Проецирование точки на три плоскости проекций. Комплексный чертеж точки.
Получили эпюр Монжа для трех плоскостей или комплексный чертеж точки А
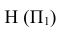
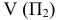
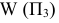
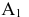
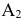
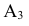
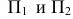
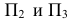
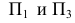
Две проекции точки лежат на одной линии связи, перпендикулярной оси.
Отрезки проецирующих линий от точки А до плоскостей проекций — координаты точки 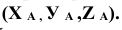
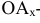
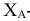
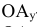
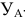
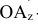
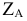
Проецирование на плоскости координат
Плоскости координат могут в пространстве располагаться произвольно. Принято одну из плоскостей располагать горизонтально, а две другие — вертикально. Одну из вертикальных плоскостей координат располагают перед наблюдателем (фронтально).
Зададим (Рис. 1.3) прямоугольную систему координат 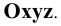
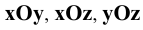
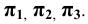
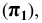
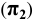
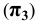
Возьмём произвольную точку 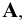
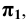
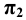
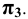
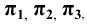
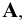
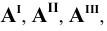
Каждая пара проецирующих лучей определяет плоскость, параллельную плоскости координат и, следовательно, перпендикулярную к соответствующей оси координат. Так плоскость 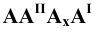
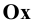
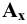
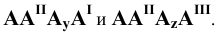
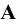
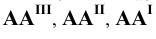
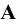
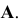
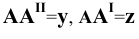
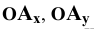
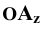
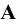
Таким образом, положение точки 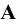
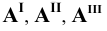
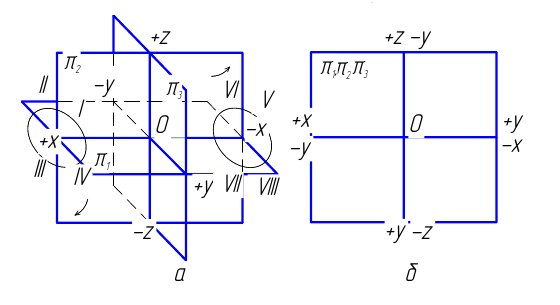
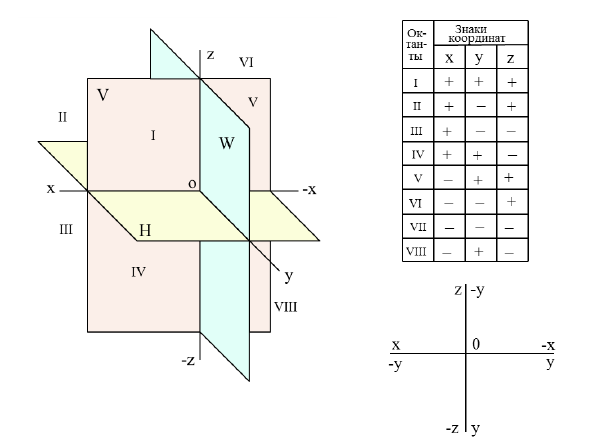
В общем случае плоскости 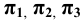
Причём для правой системы координат, изображённой на Рис. 1.4, а принята следующая нумерация углов:
- I угол — левый, передний, верхний (х, у, z);
- II угол — левый, задний, верхний (х, -у, z);
- III угол — левый, задний, нижний (х, -у, -z);
- IV угол — левый, передний, нижний (х, y,-z);
- V угол — правый, передний, верхний (-х, у, z);
- VI угол — правый, задний, верхний (-х,-у, z);
- VII угол — правый, задний, нижний (-х, -у, -z);
- VIII угол — правый, передний, нижний (-x, y, -z);
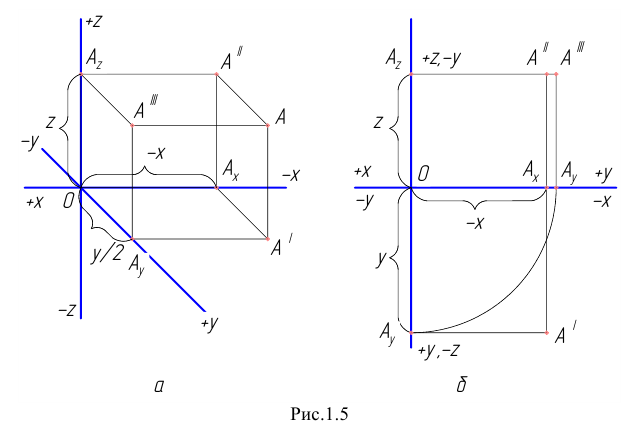
Практически изображение выполняется на одной плоскости (листе бумаги, доске и т. п.), называемой плоскостью чертежа. С этой целью плоскость 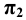
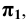
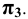
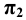
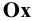
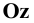
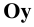
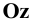
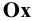
Проецируемая точка может располагаться в любом из координатных углов (октантов). Поэтому для построения её проекций кроме численных значений координат необходимо учитывать их знаки.
Рассмотрим случай общего положения точки, т.е. случай, когда требуется построить проекции точки 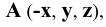
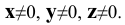
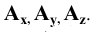
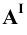
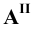
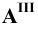
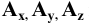
По полученному чертежу легко установить, что данная точка 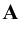
Построим прямоугольные проекции точки 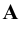
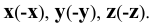
При этом координата 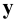
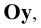
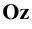
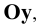
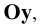
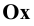

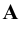
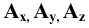
Отметим, что в прямоугольных проекциях горизонтальная 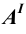
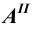
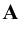
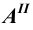
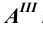
Изображения, полученные при совмещении плоскостей проекций с плоскостью чертежа, называются эпюрами. Эпюр (эпюра) — чертёж, на котором пространственная фигура изображена методом ортогональных проекций на три плоскости; эпюр позволяет определить форму и размеры проецируемого предмета, так как координаты 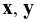
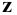
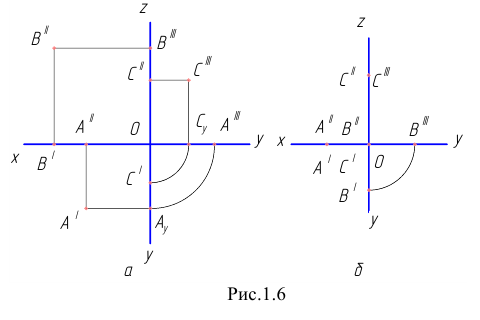
В частных случаях точка может быть расположена в одной из плоскостей координат или лежать на одной из осей (Рис. 1.6, а, б). При этом, если точка лежит в плоскости координат, то её проекция на данную плоскость совпадает с самой точкой, а две другие её проекции расположены на осях координат (см. Рис. 1.6, а). Если же точка лежит на оси координат, то две её проекции совпадают с самой точкой, а третья совпадает с началом координат (см. Рис. 1.6, б).
Аксонометрические проекции
Если оси прямоугольной системы координат и отнесённый к ним предмет спроецировать центрально или параллельно на некоторую плоскость, то полученное изображение называется аксонометрией. Рассмотрим наиболее часто употребляемые на практике виды аксонометрических проекций.
Косоугольным аксонометрическим проецированием на фронтальную плоскость называют косоугольное проецирование на плоскость, совмещённую с плоскостью 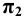
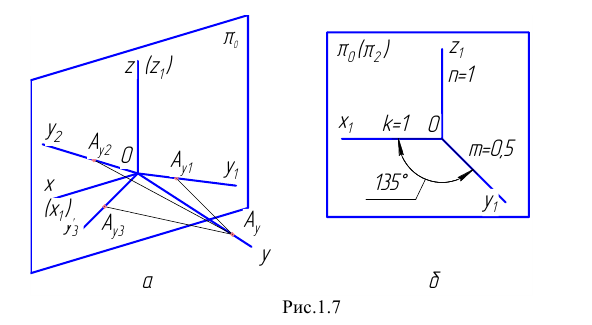
Возьмём прямоугольную координатную систему (Рис. 1.7, а) и спроецируем её косоугольно на плоскость 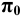
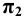
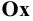
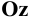
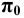
Для этого выберем на оси 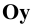
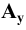
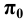
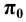
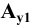
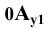
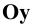
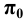
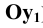
Если изменять направление проецирования, то на плоскости 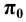
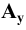
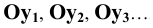
Обозначим: k — коэффициент искажения для оси 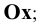
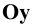
При косоугольном проецировании на фронтальную плоскость (см. Рис. 1.7, а, б) имеем 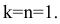
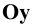
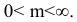
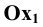
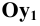
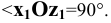
Иногда данную проекцию называют косоугольной диметрией в связи с тем, что два измерения по оси 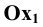
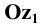
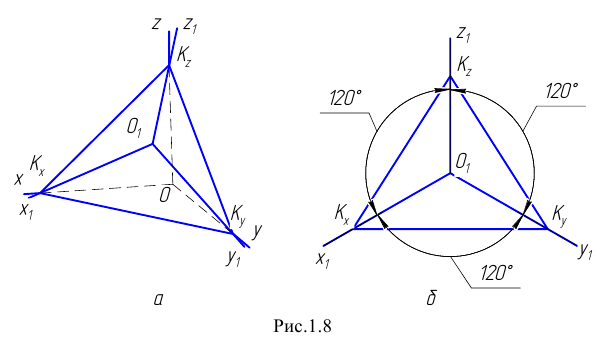
Прямоугольной изометрией называют случай прямоугольного проецирования на плоскость, одинаково наклонённую к трём плоскостям проекций. Такая плоскость проекций пересекает оси координат на равных расстояниях от начала координат.
Изобразим (Рис. 1.8, а) прямоугольную координатную систему 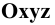
Соединим попарно прямыми линиями точки 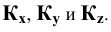
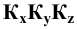
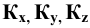
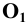
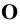
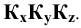
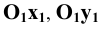
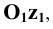
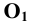
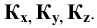
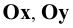
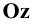
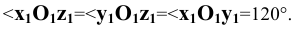
Если изометрическая проекция имеет целью выявление формы предмета (без наглядного отражения его размеров), то при построении точек допускается откладывать на осях значения координат точек с приведенными коэффициентами искажения, равными единице (k=m=n=l). При этом изображение предмета получается увеличенным в отношении 1,0/0,82=1,22.
Прямоугольной диметрией называют случай прямоугольного проецирования на плоскость, равно наклонённую к двум осям координат. Обычно проецируют на плоскость, равно наклонённую к плоскостям
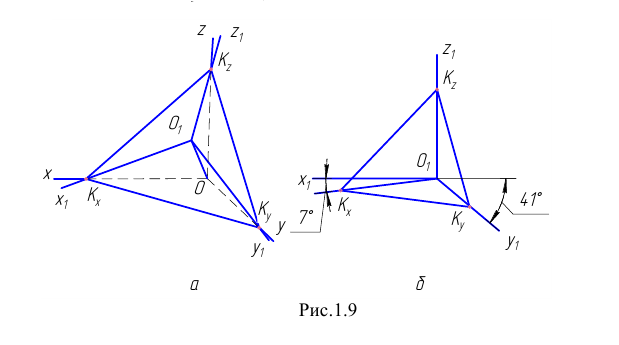
Изобразим (Рис. 1.9, а) прямоугольную координатную систему 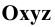
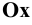
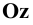
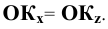
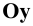
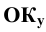
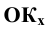
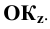
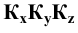
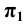
Спроецируем на неё прямоугольно начало координат ( 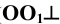
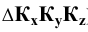
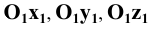
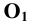
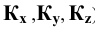
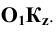
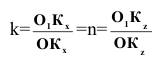
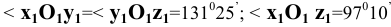
Диметрические проекции осей координат в совмещении с плоскостью чертежа показаны на Рис. 1.9, б.
Инженерная и машинная графика — одна из дисциплин, составляющих основу всего общеинженерной подготовки специалистов.
Теоретической базой инженерной и машинной графики является начертательная геометрия, позволяющая создать одно из гениальнейших изобретений человеческой мысли — чертеж. Чертеж — это своеобразный графический язык, с помощью которого, используя лишь точки, линии, геометрические знаки, буквы и цифры, изображаются самые разнообразные поверхности, машины, приборы, инженерные сооружения и т. д.
Начертательная геометрия возникла из потребностей практической деятельности человека. Задачи строительства различных сооружений, крепостных укреплений, жилья, храмов требовали предварительного их изображения. От примитивных рисунков, передававших приближенные геометрические формы сооружений, постепенно совершался переход к составлению проекционных чертежей, отражавших геометрические свойства изображаемых на них объектов.
Выдающуюся роль в развитии начертательной геометрии как науки сыграл французский геометр и инженер Гаспар Монж, который систематизировал и обобщил накопленный к тому времени опыт и теоретические познания в области изображения пространственных фигур на плоскости. В своем труде «Начертательная геометрия», изданном в 1798 году, Г. Монж дал первое научное изложение общего метода изображения пространственных фигур на плоскости.
Начертательная геометрия способствует развитию пространственного воображения и логического мышления.
Впервые отдельные правила и приемы построения изображений были систематизированы и развиты французским ученым Гаспаром Монжем (1746-1818). Изложенный Гаспаром Монжем метод параллельного проецирования является основным методом, используемым при выполнении технических чертежей в настоящее время.
Материал в учебном пособии изложен кратко в объеме, соответствующем количеству учебного времени, отведенного на изучение предмета. Теоретический материал сопровождается примерами решения задач. В конце каждой главы имеются вопросы для закрепления проработанного материала.
Может быть использовано в качестве учебного пособия при обучении студентов технического профиля очной и заочной форм обучения.
Свойства прямоугольного проецирования
- Каждая точка и прямая в пространстве имеет единственную проекцию на плоскости, так как через любую точку в пространстве можно провести только один проецирующий луч.
- Каждая точка на плоскости проекций может быть проекцией множества точек, если через них проходит общий проецирующий луч.
- Если точка принадлежит прямой, то проекция точки принадлежит проекции этой прямой.
- Отношение отрезков прямой равно отношению их проекций.
- Отношение отрезков параллельных прямых равно отношению их проекций.
- Если прямая перпендикулярна плоскости проекций, то проекцией этой прямой является точка.
- Если отрезок прямой параллелен плоскости проекций, то на эту плоскость отрезок спроецируется в натуральную величину.
Комплексный чертёж точки (эпюр точки)
Комплексный чертеж (эпюр) точки состоит из двух или трех ортогональных проекций. Эти проекции получают на взаимно перпендикулярных плоскостях проекций. Одна из плоскостей проекций Н называется горизонтальной плоскостью проекций, вторая V — фронтальной, а третья W — профильной.
Рисунок 1.3 — плоскости проекций, знаки координат
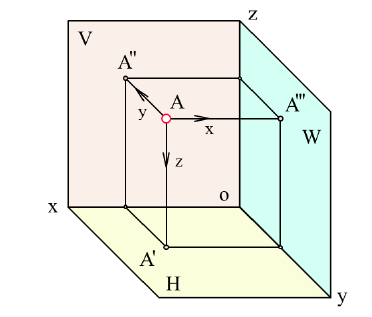
Спроецируем точку А на плоскости проекций Y, V и W. Точка А’ называется горизонтальной проекцией точки А, точка А» — ее фронтальная проекция, точка А’» — ее профильная проекция. Расстояние 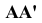
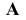
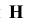
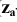
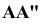
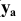
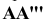
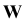
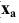
Таким образом, какая-либо точка пространства А будет определяться тремя ее координатами:
Чтобы получить плоский чертеж точки А, плоскости Н и W вращают до совмещения с плоскостью V. Прямые 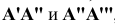
Рисунок 1.4 — Точка в системе плоскостей проекций
Рисунок 1.5 — Эпюр точки
Центральный метод проецирования
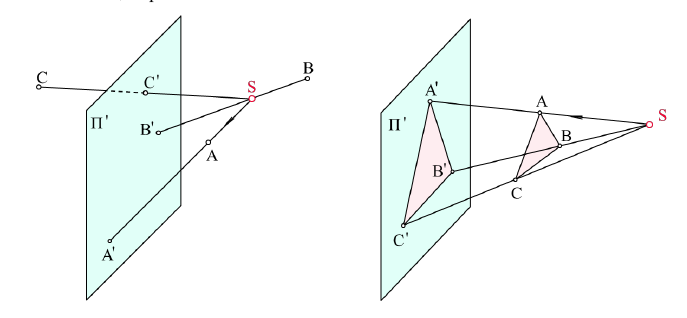
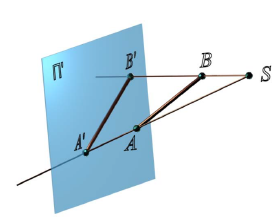
В пространстве выбирают произвольную точку S — центр проецирования и плоскость П’ — плоскость проекций или картинную плоскость (рис. 2.1). Для получения центральной проекции предмета, например отрезка [AB], необходимо через центр проекций и каждую точку предмета (точки A и B) провести прямые до пересечения с картинной плоскостью. Эти прямые называются проецирующими лучами. Точка пересечения проецирующего луча с картинной плоскостью называется проекцией точки на эту плоскость.
Проекция предмета на плоскость — это множество проекций всех его точек на заданную плоскость.
Рис. 2.1. Центральный метод проецирования:
[ SA) и [ SB) — проецирующие лучи;
A[ ‘ = ‘SA 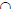
Чертежи, полученные методом центрального проецирования, отличаются большой наглядностью, поскольку построены на том же принципе, что и аппарат человеческого зрения. Однако такие чертежи сложно выполнять и измерять, поскольку размеры предмета искажаются.
Параллельный метод проецирования
Если центр проекций удалить в бесконечность, то угол между проецирующими лучами будет стремиться к нулю, и проецирующие лучи окажутся параллельными (рис. 2.2).
Рис. 2.2. Параллельный метод проецирования: s — направление проецирования;
[SA), [SB) и [SC) — проецирующие лучи;
A’, B’ и C’ — параллельные проекции точек A, B и C на плоскость П’ в направлении s
Свойства параллельных проекций
- Проекцией точки является точка (см. рис. 2.2).
- Проекцией прямой линии является прямая линия (см. рис. 2.2), за исключением случая, когда прямая параллельна направлению проецирования.
- При параллельном проецировании сохраняются пропорции.
- Если точка принадлежит какой-либо линии, то проекция этой точки принадлежит проекции этой линии C ∈ AB
C’∈ A’B’ (см. рис. 2.2).
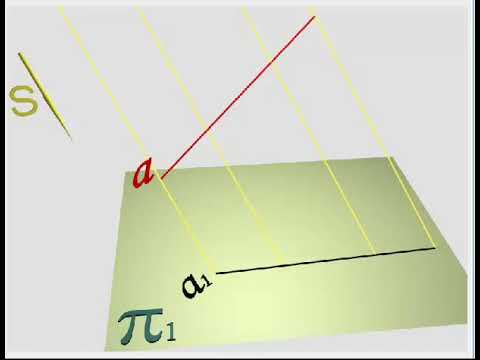
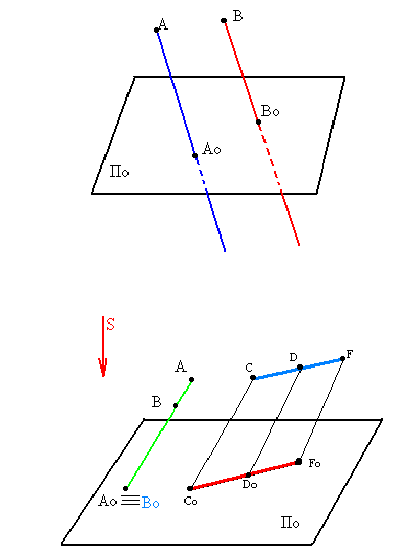
- Если прямые параллельны между собой, то их проекции также параллельны (рис. 1.3).
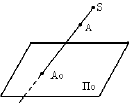
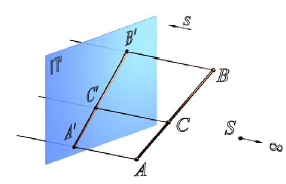
Рис. 2.3. Проекции параллельных прямых:
[AB ]//[DC] [A’ B’]//[D’ C’]
Ортогональные проекции
Если направление проецирования s перпендикулярно плоскости проекций, то метод проецирования называется ортогональным (рис. 2.4), а полученные проекции — ортогональными.
Рис. 2.4. Ортогональное проецирование:
s 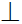
Ортогональное проецирование является частным случаем параллельного проецирования и имеет те же свойства.
Изображения, полученные при проецировании на одну плоскость проекций, не являются обратимыми, то есть задача о восстановлении оригинала по заданной проекции a´ не решается однозначно. Проекции всех точек, расположенных на проецирующем луче AA ´ на плоскость П’, совпадают.
Для получения обратимых чертежей нужны некоторые дополнительные условия. Например, изображаемый предмет жестко связывают с координатными осями и проецируют на плоскость вместе с ними. Такие чертежи называются аксонометрическими. Другой метод состоит в том, что предмет проецируют на несколько взаимно перпендикулярных плоскостей проекций. Такие чертежи называются ортогональными и именно они получили наибольшее распространение в технике.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Образование проекций
- Точка и прямая
- Прямая линия
- Плоскость
- Создание спецификации, связанной с моделью сборочного изделия, в полуавтоматическом режиме в КОМПАС — 3D
- Создание трёхмерных объектов в KOMПAC-3D
- Моделирование трехмерных объектов в KOMПAC-3D
- Метод проекций
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Лекция 1. Методы проецированияСкачать

Лекция 1. Методы проецирования
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

1.1. Центральное проецирование
Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.
Известны два метода проецирования: центральное и параллельное .
Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB, >… — проецирующего луча).
Рисунок 1.1 – Центральное проецирование
Введём следующие обозначения (Рисунок 1.1):
SA, SB – проецирующие прямые (проецирующие лучи).
Примечание: левой клавишей мыши можно переместить точку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и можно будет ее переместить по вертикали.
Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.
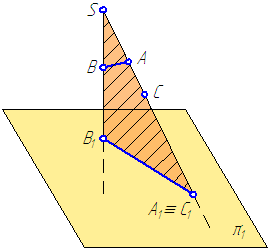
Свойство 1 . Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.
Докажем это утверждение.
На рисунке 1.1: точка А1 – центральная проекция точки А на плоскости проекций π1. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С. Центральная проекция точки С (С1) на плоскости проекций π1 совпадает с проекцией точки А (А1):
Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.
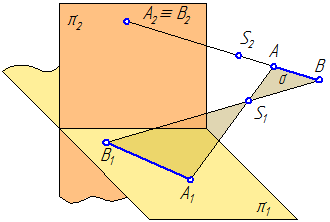
Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым, введём еще одну плоскость проекций (π2) и ещё один центр проецирования (S2) (Рисунок 1.2).
Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств
Построим проекции точки А на плоскости проекций π2. Из всех точек пространства только точка А имеет своими проекциями А1 на плоскость π1 и А2 на π2 одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В).
Свойство 2 . Проекция прямой есть прямая.
Докажем данное свойство.
Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ, задающий прямую. Треугольник ΔSAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π1=А1В1, где А1В1 – центральная проекция прямой, заданной отрезком АВ.
Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.
Видео:виды проецирования - начертательная геометрияСкачать
1.2. Параллельное проецирование
Рассмотрим метод параллельного проецирования. Наложим три ограничения, которые позволят нам, пусть и в ущерб наглядности изображения, получить чертёж более удобным для использования его на практике:
- Удалим оба центра проекции в бесконечность. Таким образом, добьемся того, что проецирующие лучи из каждого центра станут параллельными, а, следовательно, соотношение истинной длины любого отрезка прямой и длины его проекции будут зависеть только от угла наклона этого отрезка к плоскостям проекций и не зависят от положения центра проекций;
- Зафиксируем направление проецирования относительно плоскостей проекций;
- Расположим плоскости проекций перпендикулярно друг другу, что позволит легко переходить от изображения на плоскостях проекций к реальному объекту в пространстве.
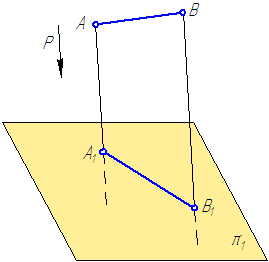
Таким образом, наложив эти ограничения на метод центрального проецирования, мы пришли к его частному случаю – методу параллельного проецирования (Рисунок 1.3).Проецирование, при котором проецирующие лучи, проходящие через каждую точку объекта, параллельно выбранному направлению проецирования P, называется параллельным.
Рисунок 1.3 – Метод параллельного проецирования
Проведём через точки А и В проецирующие лучи, параллельные заданному направлению проецирования Р. Проецирующий луч проведённый через точку А пересечёт плоскость проекций π1 в точке А1. Аналогично проецирующий луч, проведённый через точку В пересечет плоскость проекций в точке В1. Соединив точки А1 и В1, получим отрезок А1 В1– проекция отрезка АВ на плоскость π1.
Видео:Проецирование прямой общего положенияСкачать

1.3. Ортогональное проецирование. Метод Монжа
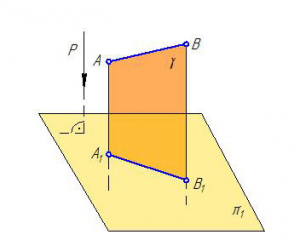
Если направление проецирования Р перпендикулярно плоскости проекций p1, то проецирование называется прямоугольным (Рисунок 1.4), или ортогональным (греч. ortos – прямой, gonia – угол), если Р не перпендикулярно π1, то проецирование называется косоугольным .
Четырехугольник АА1В1В задаёт плоскость γ, которая называется проецирующей, поскольку она перпендикулярна к плоскости π1 (γ⊥π1). В дальнейшем будем использовать только прямоугольное проецирование.
Рисунок 1.4 – Ортогональное проецирование
Рисунок 1.5- Монж, Гаспар (1746-1818)
Основоположником ортогонального проецирования считается французский учёный Гаспар Монж (Рисунок 1.5).
До Монжа строители, художники и учёные обладали довольно значительными сведениями о проекционных способах, и, всё же, только Гаспар Монж является творцом начертательной геометрии как науки.
Гаспар Монж родился 9 мая 1746 года в небольшом городке Боне (Бургундия) на востоке Франции в семье местного торговца. Он был старшим из пяти детей, которым отец, несмотря на низкое происхождение и относительную бедность семьи, постарался обеспечить самое лучшее образование из доступного в то время для выходцев из незнатного сословия. Его второй сын, Луи, стал профессором математики и астрономии, младший — Жан также профессором математики, гидрографии и навигации. Гаспар Монж получил первоначальное образование в городской школе ордена ораторианцев. Окончив её в 1762 году лучшим учеником, он поступил в колледж г. Лиона, также принадлежавший ораторианцам. Вскоре Гаспару доверяют там преподавание физики. Летом 1764 года Монж составил замечательный по точности план родного города Бона. Необходимые при этом способы и приборы для измерения углов и вычерчивания линий были изобретены самим составителем.
Во время обучения в Лионе получил предложение вступить в орден и остаться преподавателем колледжа, однако, вместо этого, проявив большие способности к математике, черчению и рисованию, сумел поступить в Мезьерскую школу военных инженеров, но (из-за происхождения) только на вспомогательное унтер-офицерское отделение и без денежного содержания. Тем не менее, успехи в точных науках и оригинальное решение одной из важных задач фортификации (о размещении укреплений в зависимости от расположения артиллерии противника) позволили ему в 1769 году стать ассистентом (помощником преподавателя) математики, а затем и физики, причём уже с приличным жалованием в 1800 ливров в год.
В 1770 году в возрасте 24-х лет Монж занимает должность профессора одновременно по двум кафедрам — математики и физики, и, кроме того, ведёт занятия по резанию камней. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке – начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года, книга вышла под названием Начертательная геометрия (Géométrie descriptive) (стенографическая запись этих лекций была сделана в 1795 году). Изложенный в ней подход к чтению лекций по этой науке и выполнению упражнений сохранился до наших дней. Еще один значительный труд Монжа – Приложение анализа к геометрии (L’application de l’analyse à la géometrie, 1795) – представляет собой учебник аналитической геометрии, в котором особый акцент делается на дифференциальных соотношениях.
В 1780 был избран членом Парижской академии наук, в 1794 стал директором Политехнической школы. В течение восьми месяцев занимал пост морского министра в правительстве Наполеона, заведовал пороховыми и пушечными заводами республики, сопровождал Наполеона в его экспедиции в Египет (1798–1801). Наполеон пожаловал ему титул графа, удостоил многих других отличий.
Метод изображения объектов по Монжу заключается в двух основных моментах:
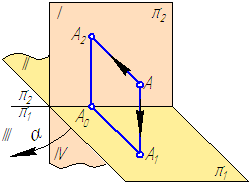
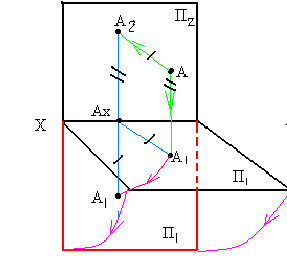
1. Положение геометрического объекта в пространстве, в данном примере точки А, рассматривается относительно двух взаимно перпендикулярных плоскостей π1 и π2 (Рисунок 1.6).
Они условно разделяют пространство на четыре квадранта. Точка А расположена в первом квадранте. Декартова система координат послужила основой для проекций Монжа. Монж заменил понятие координатных осей проекций на линию пересечения плоскостей проекций (ось проекций) и предложил совместить координатные плоскости в одну путем поворота их вокруг координатных осей.
Рисунок 1.6 – Модель построения проекций точки
π1 – горизонтальная (первая) плоскость проекций
π2 – фронтальная (вторая) плоскость проекций
Рассмотрим пример проецирования точки А на две взаимно перпендикулярные плоскости проекций π1 и π2.
Опустим из точки А перпендикуляры (проецирующие лучи) на плоскости π1 и π2 и отметим их основания, то есть точки пересечения этих перпендикуляров (проецирующих лучей) с плоскостями проекций. А1 – горизонтальная (первая) проекция точки А;А2 – фронтальная (вторая) проекция точки А; АА1 и АА2 – проецирующие прямые. Стрелки показывают направление проецирования на плоскости проекций π1 и π2. Такая система позволяет однозначно определить положение точки относительно плоскостей проекций π1 и π2:
2. Совместим поворотом вокруг оси проекций π2/π1 плоскости проекций в одну плоскость (π1 с π2), но так, чтобы изображения не накладывались друг на друга, (в направлении α, Рисунок 1.6), получим изображение, называемое прямоугольным (ортогональным) чертежом (Рисунок 1.7):
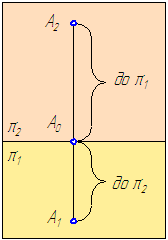
Рисунок 1.7 – Ортогональный чертеж
Прямоугольный или ортогональный носит название эпюр Монжа .
Прямая А2А1 называется линией проекционной связи , которая соединяет разноимённые проекции точки (А2 — фронтальную и А1 — горизонтальную) всегда перпендикулярна оси проекций (оси координат) А2А1⊥π2/π1. На эпюре отрезки, обозначенные фигурными скобками, представляют собой:
Видео:Методы проецированияСкачать

1.4. Прямоугольные проекции точки. Свойства ортогонального чертежа
1. Две прямоугольные проекции точки лежат на одной линии проекционной связи, перпендикулярной к оси проекций.
2. Две прямоугольные проекции точки однозначно определяют её положение в пространстве относительно плоскостей проекций.
Убедимся в справедливости последнего утверждения, для чего повернём плоскость π1 в исходное положение (когда π1⊥π2). Для того, чтобы построить точку А необходимо из точек А1 и А2 восстановить проецирующие лучи, а фактически – перпендикуляры к плоскостям π1и π2, соответственно. Точка пересечения этих перпендикуляров фиксирует в пространстве искомую точку А. Рассмотрим ортогональный чертеж точки А (Рисунок 1.8).
Рисунок 1.8 – Построение эпюра точки
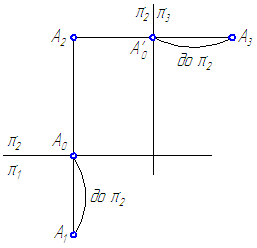
Введём третью (профильную) плоскость проекций π3 перпендикулярную π1 и π2 (задана осью проекций π2/π3).
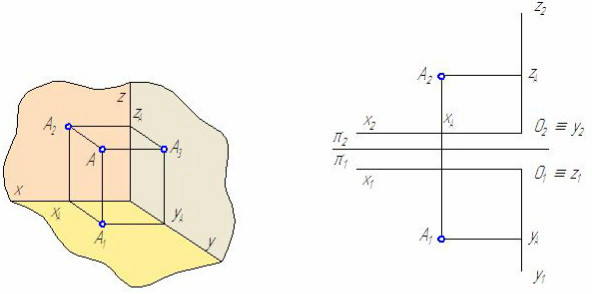
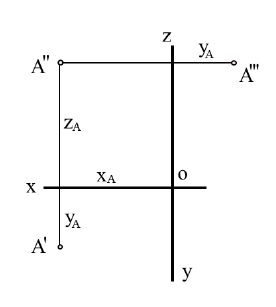
Расстояние от профильной проекции точки до вертикальной оси проекций А‘0A3 позволяет определить расстояние от точки А до фронтальной плоскости проекций π2. Известно, что положение точки в пространстве можно зафиксировать относительно декартовой системы координат с помощью трёх чисел (координат) A(XA; YA; ZA) или относительно плоскостей проекций с помощью её двух ортогональных проекций (A1=(XA; YA); A2=(XA; ZA)). На ортогональном чертеже по двум проекциям точки можно определить три её координаты и, наоборот, по трём координатам точки, построить её проекции (Рисунок 1.9, а и б).
а б
Рисунок 1.9 – Построение эпюра точки по её координатам
По расположению на эпюре проекций точки можно судить о её расположении в пространстве:
- если на эпюре горизонтальная проекция точки А — А1 лежит под осью координат X , а фронтальная — А2 – над осью X, то можно говорить, что точка А принадлежит 1-му квадранту;
- если на эпюре горизонтальная проекция точки А — А1 лежит над осью координат X, а фронтальная — А2 – под осью X, то точка А принадлежит 3-му квадранту;
- если на эпюре горизонтальная и фронтальная проекции точки А — А1 и А2 лежат над осью X, то точка А принадлежит 2-му квадранту;
- если на эпюре горизонтальная и фронтальная проекции точки А — А1 и А2 лежат под осью X, то точка А принадлежит 4-му квадранту;
- если на эпюре проекция точки совпадает с самой точкой, то значит – точка принадлежит плоскости проекций;
- точка, принадлежащая плоскости проекций или оси проекций (оси координат), называется точкой частного положения.
Для определения в каком квадранте пространства расположена точка, достаточно определить знак координат точки.
| X | Y | Z | |
|---|---|---|---|
| I | + | + | + |
| II | + | — | + |
| III | + | — | — |
| IV | + | + | — |
Видео:Лекция 1. Классификация прямых линий.Скачать

Упражнение
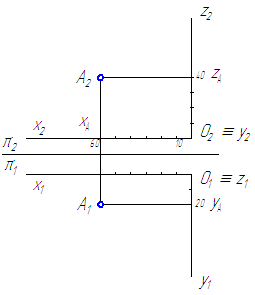
Построить ортогональные проекции точки с координатами А (60, 20, 40) и определить в каком квадранте расположена точка .
Решение задачи: по оси OX отложить значение координаты XA=60, затем через эту точку на оси OX восстановить линию проекционной связи, перпендикулярную к OX, по которой вверх отложить значение координаты ZA=40, а вниз – значение координаты YA=20 (Рисунок 1.10). Все координаты положительные, значит точка расположена в I квадранте.
Рисунок 1.10 – Решение задачи
Видео:Лекция 2. Проецирование прямого угла.Скачать

1.5. Задачи для самостоятельного решения
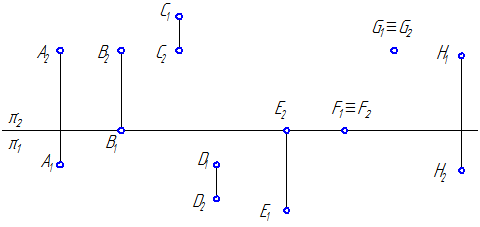
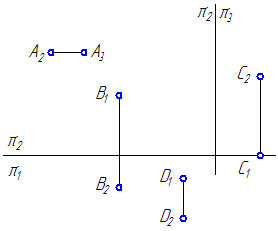
1. По эпюру определите положение точки относительно плоскостей проекций (Рисунок 1.11).
Рисунок 1.11
2. Достройте недостающие ортогональные проекции точек А, В, С на плоскости проекций π1, π2, π3 (Рисунок 1.12).
Рисунок 1.12
3. Постройте проекции точки:
- Е, симметричной точке А относительно плоскости проекций π1;
- F, симметричной точке В относительно плоскости проекций π2;
- G, симметричной точке С относительно оси проекций π2/π1;
- H, симметричной точке D относительно биссекторной плоскости второго и четвертого квадрантов.
4. Постройте ортогональные проекции точки К, расположенной во втором квадранте и удаленной от плоскостей проекций π1 на 40 мм, от π2 — на 15 мм.
🌟 Видео
Следы прямой Взаимное положение двух прямыхСкачать

виды проецирования и свойства параллельного проецированияСкачать
тема 8 3 Параллельное проектирование и его свойстваСкачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Инженерная графика Метод проецированияСкачать

Параллельное проектирование и его свойстваСкачать

Параллельность прямых. 10 класс.Скачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Параллельная проекцияСкачать

Лекция №1, 2-я часть. Методы проецирования. Решение задач.Скачать

Проецирование прямых частного положенияСкачать

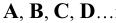
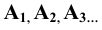
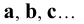
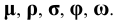
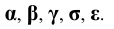
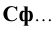
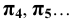
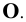
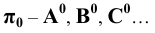
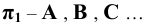
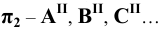
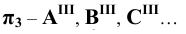
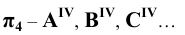
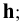
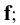
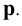
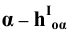
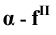
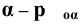
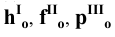
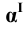 — горизонтально — проецирующая плоскость
— горизонтально — проецирующая плоскость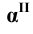 — фронтально — проецирующая плоскость
— фронтально — проецирующая плоскость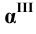 — профильно — проецирующая плоскость
— профильно — проецирующая плоскость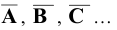
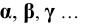
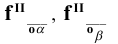
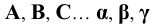
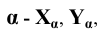
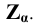
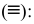
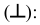
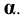
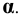
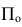 — плоскость проекций
— плоскость проекций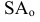 — проецирующий луч (проецирующая прямая)
— проецирующий луч (проецирующая прямая)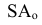 — центральная проекция точки А на плоскость
— центральная проекция точки А на плоскость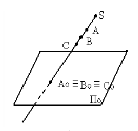
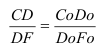
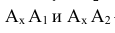
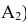
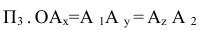
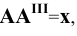
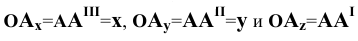
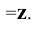
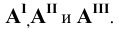
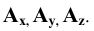
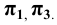
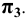
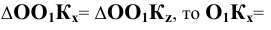
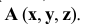
 C’∈ A’B’ (см. рис. 2.2).
C’∈ A’B’ (см. рис. 2.2).