Видео:Периметр равнобедренного треугольникаСкачать

Формула
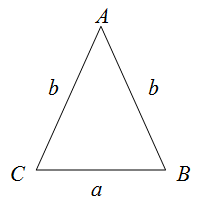
Чтобы найти периметр равнобедренного треугольника $ABC$, нужно к длине его основание прибавить удвоенную длину боковой стороны.
Периметр равнобедренного треугольника — это сумма длин его сторон. У равнобедренного треугольника боковые стороны равны. Поэтому если $a$ — длина основания равнобедренного треугольника, а $b$ — длина боковых сторон, то периметр равен
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Примеры вычисления периметра равнобедренного треугольника
Задание. В равнобедренном треугольнике $ABC$ основание равно 7 м, а длины боковых сторон — 4 м. Найти его периметр.
Решение. Воспользуемся формулой для нахождения периметра равнобедренного треугольника
Тогда искомый периметр равен:
Ответ. $P_=15$ (м)
Задание. Найти периметр равнобедренного треугольника $ABC$, если его основание равно $a=8$ см и каждая из боковых сторон $b$ составляют 75% от основания.
Решение. Найдем длину боковой стороны, для этого найдем 75% от длины основания:
$b=8 cdot 0,75=6$ (см)
Для вычисления периметра равнобедренного треугольника воспользуемся формулой:
Тогда периметр $ABC$ равен:
Ответ. $P_=20$ (см)
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Формула периметра равнобедренного треугольника
Периметр равнобедренного треугольника ABC , длины сторон которого соответственно равны: боковые стороны AB = BC = a , основание AC = b вычисляется по формуле:
Периметр равнобедренного треугольника вычисляется по формуле:
( P_ = a + b + c = 2 cdot a + b)
где a,b,c – стороны равнобедренного треугольника.
Основные понятия, справедливые для треугольников
- Сумма углов треугольника равна 180°.
- Высота – это отрезок перпендикуляра, опущенного из вершины на противоположную сторону.
- Центр описанной окружности лежит на пересечении медиатрис.
- Медиатриса – это перпендикулярна прямая, проходящая через середину стороны.
- Центр вписанной окружности лежит на пересечении биссектрис углов.
- Биссектриса угла делит угол на две равные части.
- Медиана – это отрезок, соединяющий вершину с серединой противоположной стороны.
- Медианы пересекаются в центре тяжести, который делит каждую медиану в отношение 2:1.
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
© 2022 Все калькуляторы online
Копирование материалов запрещено
Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Периметр равнобедренного треугольника

Средняя оценка: 4.5
Всего получено оценок: 122.
Средняя оценка: 4.5
Всего получено оценок: 122.
Периметр – это сумма длин всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это вытекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и вытекает формула периметра:
P=2a+b, где b – это основание треугольника, a – значение боковой стороны.
Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. Рассмотрим несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра.
Видео:№108. Периметр равнобедренного треугольника ABC с основанием ВС равен 40 см, а периметрСкачать

Задача 1
- В равнобедренном треугольнике основание равно 6, а высота, проведенная к этому основанию, равна 4. Необходимо найти периметр фигуры.
Высота равнобедренного треугольника, проведенная к основанию, является также медианой и биссектрисой. Это свойство очень часто используется при решении задач, связанных с равнобедренными треугольниками.
Треугольник АВС высотой ВM делится на два прямоугольных треугольника: АВM и ВСM. В треугольнике АВM катет ВM известен, катет АM равен половине основания треугольника АВС, так как ВM является медианой, биссектрисой и высотой. По теореме Пифагора найдем значение гипотенузы АВ.
Найдем периметр: P=AC+AB*2=6+5*2=16
Видео:Урок. Как найти периметр равностороннего треугольника. Математика 2 класс. #учусьсамСкачать

Задача 2
- В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам. нужно найти периметр треугольника.
Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)==$$ – синус 30 градусов является табличным значением.
Выразим нужную сторону:
Через котангенс найдем значение AH:
$$AH=<BHoversqrt>=10*sqrt=17,32$$ – получившееся значение округлим до сотых.
Теперь, когда все требуемые значения найдены, определим периметр:
Видео:Периметр равнобедренного треугольникаСкачать

Задача 3
- В равнобедренном треугольнике ABC известна площадь, которая равна $$16oversqrt$$ и острый угол при основании 30 градусов. Найти периметр треугольника.
Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.
Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято.
Подставим полученное значение в формулу площади.
Подставим значение a в формулу площади и определим значение высоты:
Через теорему Пифагора найдем боковую сторону треугольника:
Подставим значения в формулу периметра:
Видео:Площадь равнобедренного треугольникаСкачать

Что мы узнали?
Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.
💡 Видео
№253. Периметр равнобедренного треугольника равен 25см, разность двух сторон равна 4 см, а одинСкачать

Свойства равнобедренного треугольника. Практическая часть. 7 класс.Скачать

Периметр равнобедренного треугольника равен 240. ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Свойства равнобедренного треугольника. 7 класс.Скачать

Площадь равнобедренного треугольникаСкачать
Периметр равнобедренного треугольника равен 250 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Равнобедренный треугольник. 7 класс.Скачать

Найдите площадь равнобедренного треугольника, основание которого равно 12 см, а боковая сторона 10.Скачать

КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать