Геометрические парадоксы невозможный треугольник

Презентация была опубликована 8 лет назад пользователемmatem43.narod.ru

Похожие презентации

Видео:РАСКРЫТ НЕВЕРОЯТНЫЙ ПАРАДОКС С ТРЕУГОЛЬНИКАМИСкачать

Презентация на тему: » Геометрические парадоксы Парадокс-явление, кажущееся невероятным и неожиданным. Геометрические парадоксы основаны на том, что наш мозг всегда пытается.» — Транскрипт:

1 Геометрические парадоксы Парадокс-явление, кажущееся невероятным и неожиданным. Геометрические парадоксы основаны на том, что наш мозг всегда пытается представить нарисованные на бумаге двухмерные рисунки как трехмерные.

2 Основные типы геометрических парадоксов «Невозможный треугольник» «Бесконечная лестница» «Космическая вилка» «Сумасшедший ящик»

3 «Невозможный треугольник» Первую невозможную фигуру изобразил шведский художник Оскар Реутерсвард в 1934 году. Шведское правительство решило увековечить три картины художника на почтовых марках, одной из них стал и невозможный треугольник.

4 Трибар Трибар – разновидность невозможного треугольника. Его авторы — отец и сын Лайонелл и Роджер Пенроузы, генетик и математик. Трибар появился в 1958 году в журнале British Journal of Psychology, в статье под заголовком «Удивительные фигуры, особый вид оптических иллюзий».

5 Литография М.Эшера «Водопад» основана на фигуре невозможного треугольника. В этой работе два невозможных треугольника соединены в единую невозможную фигуру. Создается впечатление, что водопад является замкнутой системой, работающей по типу вечного двигателя, нарушая закон сохранения энергии.

6 «Бесконечная лестница» Эту фигуру называют еще «Вечной лестницей», «Непрерывно восходящей и нисходящей тропой» или «Лестницей Пенроуза» – по имени ее создателей. Впервые эта фигура была опубликована в 1958 году Лайонелом и Роджером Пенроузами в British Journal of Psychology. Перед нами предстает лестница, ведущая, казалось бы, вверх или вниз, но при этом человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути.

7 «Бесконечной лестницей» с успехом воспользовался художник М. Эшер в своей литографии «Восхождение и нисхождение«(1960 году) Вполне узнаваемая «Бесконечная лестница» аккуратно вписана в крышу монастыря. Монахи непрерывно движутся по лестнице в направлении по часовой стрелке и против нее. Они идут навстречу друг другу по невозможному пути. Им так и не удается ни подняться наверх, ни спуститься вниз.

8 «Космическая вилка» Этот невозможный объект с тремя (или двумя?) зубцами стал популярен у инженеров и любителей головоломок в 1964 году. Впервые он появился в печати как часть рекламы California Technical Industries 23 марта 1964 года в номере журнала Aviation Week and Space Technology.

9 «Сумасшедший ящик» «Сумасшедший ящик» – это вывернутый наизнанку каркас куба. Фигуру можно воспринять двояко. Как и многие другие невозможные объекты, «Сумасшедший ящик» основан на неправильных соединениях, допущенных при рисовании.

10 Непосредственным предшественником «Сумасшедшего ящика» была «невозможная коробка», которую держит сидящий мальчик в знаменитой гравюре М. Эшера «Бельведер» (1958). Предшественником невозможной коробки Эшера был, в свою очередь, куб Неккера.

11 Куб Неккера был впервые описан в 1832 году швейцарским кристаллографом Льюисом А. Неккером, который заметил, что кристаллы иногда зрительно меняют форму, когда на них смотришь. Он не является невозможным объектом, однако представляет собой фигуру, в, которой параметр глубины может восприниматься неоднозначно. Когда мы вглядываемся в куб, то замечаем, что голубая грань куба находится то на переднем, то на заднем плане.

12 Имп-Арт – искусство парадоксальных картин Многие известные художники рисовали работы, в основе которых лежали геометрические парадоксы. Эти работы выделяют в отдельное направление изобразительного искусства — «имп-арт», от английских слов impossible («невозможный») и art («искусство»). Художнику требуется определённое мастерство, чтобы убедить зрителя в наличии объёма, перспективы, создать иллюзию пространства в своём произведении. «Рисовать – значит обманывать» – эти слова М.К. Эшера исполнены глубокого смысла. Невозможные фигуры дают почувствовать масштабы этого обмана.

13 Геометрические парадоксы и психология Очень интересно наблюдать за человеком, рассматривающим невозможный объект, и так же интересно наблюдать за тем, как он пытается понять его. Невозможные объекты важны для психологов, выясняющих, что же привлекает внимание людей.

Видео:Самая сложная задача из самой сложной олимпиады [3Blue1Brown]Скачать

Парадоксальный мир невозможных объектов

Наши глаза познавать не умеют
природу предметов.
А потому не навязывай им
заблуждений рассудка.

Тит Лукреций Кар

Расхожее выражение «обман зрения» по сути своей неверно. Глаза не могут обмануть нас, поскольку являются только промежуточным звеном между объектом и мозгом человека. Обман зрения обычно возникает не из-за того, что мы видим, а из-за того, что бессознательно рассуждаем и невольно заблуждаемся: «посредством глаза, а не глазом смотреть на мир умеет разум».

Одним из наиболее эффектных направлений художественного течения оптического искусства (op-art) является имп-арт (imp-art, impossible art), основанный на изображении невозможных фигур. Невозможные объекты представляют собой рисунки на плоскости (любая плоскость двухмерна), изображающие трехмерные структуры, существование которых в реальном трехмерном мире невозможно. Классической и одной из самых простых фигур является невозможный треугольник.

В невозможном треугольнике каждый угол сам по себе является возможным, но парадокс возникает, когда мы рассматриваем его целиком. Стороны треугольника направлены одновременно и к зрителю, и от него, поэтому отдельные его части не могут образовать реальный трехмерный объект.

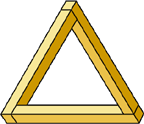Невозможный треугольник Пенроуза	Треугольник, воспринимаемый как «возможный»

Собственно говоря, наш мозг интерпретирует рисунок на плоскости как трехмерную модель. Сознание задает «глубину», на которой находится каждая точка изображения. Наши представления о реальном мире сталкиваются с противоречием, с некоей непоследовательностью, и приходится делать некоторые допущения:

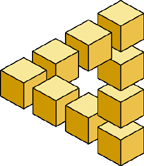Треугольник Рейтерсвэрда

• прямые двухмерные линии интерпретируются как прямые трехмерные линии;
• двухмерные параллельные линии интерпретируются как трехмерные параллельные линии;
• острые и тупые углы интерпретируются как прямые углы в перспективе;
• внешние линии рассматриваются как граница формы. Эта внешняя граница чрезвычайно важна для построения полного изображения.

Человеческое сознание сначала создает общее изображение предмета, а затем рассматривает отдельные части. Каждый угол совместим с пространственной перспективой, но, воссоединившись, они образуют пространственный парадокс. Если закрыть любой из углов треугольника, то невозможность пропадает.

Видео:ПАРАДОКС ЛЕСТНИЦЫ | ПИФАГОР ОШИБАЛСЯ? | ТЕОРЕМА НЕ ВЕРНА?Скачать

История невозможных фигур

Ошибки пространственного построения встречались у художников и тысячу лет тому назад. Но первым построившим и проанализировавшим невозможные объекты по праву считается шведский художник Оскар Рейтерсвэрд (Oscar Reutersvärd), нарисовавший в 1934 г. первый невозможный треугольник, состоявший из девяти кубиков.

Водопад Эшера	«Москва», графика (тушь, карандаш), 50х70 см, 2003 г.

Независимо от Рейтерсвэрда английский математик и физик Роджер Пенроуз повторно открывает невозможный треугольник и публикует его изображение в британском журнале по психологии в 1958 г. В иллюзии использована «ложная перспектива». Иногда такую перспективу называют китайской, так как подобный способ рисования, когда глубина рисунка «двусмысленна», часто встречался в работах китайских художников.

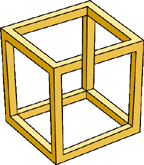Невозможный куб

В 1961 г. голландец М. Эшер (Maurits C. Escher), вдохновленный невозможным треугольником Пенроуза, создает известную литографию «Водопад». Вода на картине течет бесконечно, после водяного колеса она проходит дальше и попадает обратно в исходную точку. По сути это изображение вечного двигателя, но любая попытка в реальности построить данную конструкцию обречена на неудачу.

С тех пор невозможный треугольник не раз использовался в работах других мастеров. Помимо уже упомянутых можно назвать бельгийца Жоса де Мея (Jos de Mey), швейцарца Сандро дель Пре (Sandro del Prete) и венгра Иштвана Ороса (Istvan Orosz).

Как из отдельных пикселов на экране формируются изображения, так и из основных геометрических фигур можно создавать объекты невозможной реальности. Например, рисунок «Москва», на котором изображена не совсем обычная схема московского метрополитена. Сначала мы воспринимаем изображение целиком, но прослеживая взглядом отдельные линии, убеждаемся в невозможности их существования.

«Три улитки (RDL-куб)», графика (тушь, карандаш), 50х70 см, 2003 г.

На рисунке «Три улитки» маленький и большой кубы ориентированы не в нормальной изометрической проекции. Меньший по размерам куб сопрягается с большим по передним и задним сторонам, а значит, следуя трехмерной логике, он имеет такие же размеры некоторых сторон, что и большой. Сначала рисунок кажется реальным представлением твердого тела, но по мере анализа выявляются логические противоречия этого объекта.

Рисунок «Три улитки» продолжает традиции второй знаменитой невозможной фигуры — невозможного куба (ящика).

«IQ», графика (тушь, карандаш), 50х70 см, 2001 г.	«Вверх и вниз», М. Эшер

Сочетание различных объектов можно найти и в не совсем серьезном рисунке «IQ» (intelligence quotient — коэффициент интеллекта). Интересно, что некоторые люди не воспринимают невозможные объекты из-за того, что их сознание не способно отождествлять плоские картины с трехмерными объектами.

Дональд Е. Симанек высказал мнение, что понимание визуальных парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Многие работы с парадоксальными объектами можно отнести к «интеллектуальным математическим играм». Современная наука говорит о 7-мерной или 26-мерной модели мира. Моделировать подобный мир можно только с помощью математических формул, человек представить его просто не в состоянии. И здесь оказываются полезными невозможные фигуры. С философской точки зрения они служат напоминанием о том, что любые явления (в системном анализе, науке, политике, экономике и т. д.) следует рассматривать во всех сложных и неочевидных взаимосвязях.

Компьютерная графика на основе картины «Невозможный алфавит», 70х50 см, 1999 г.

Разнообразные невозможные (и возможные) объекты представлены на картине «Невозможный алфавит».

Третьей популярной невозможной фигурой является невероятная лестница, созданная Пенроузом. Вы будете по ней непрерывно или подниматься (против часовой стрелки) или спускаться (по часовой стрелке). Модель Пенроуза легла в основу знаменитой картины М. Эшера «Вверх и вниз» («Ascending and Descending»).

Существует еще одна группа объектов, реализовать которые не получится. Классической фигурой является невозможный трезубец, или «чертова вилка».

При внимательном изучении картинки можно заметить, что три зубца постепенно переходят в два на едином основании, что приводит к конфликту. Мы сравниваем количество зубцов сверху и снизу и приходим к выводу о невозможности объекта.

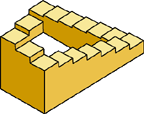Невероятная лестница Пенроуза	«Чертова вилка»

Есть ли какая-либо более существенная польза от невозможных рисунков, чем игра ума? В некоторых больницах специально развешивают изображения невозможных объектов, поскольку их рассматривание способно надолго занять больных. Логично было бы развесить такие рисунки в кассах, в милиции и прочих местах, где ожидание своей очереди длится порой целую вечность. Рисунки могли бы выступить в роли этаких «хронофагов», т.е. пожирателей времени.

Видео:Как это решить?Скачать

Что такое невозможный треугольник

Невозможный треугольник — один из удивительных математических парадоксов. При первом взгляде на него ни на секунду не можешь усомниться в его реальном существовании. Однако это только иллюзия, обман. А саму возможность такой иллюзии объяснит нам математика!

Видео:Невозможные Объекты | Vsauce3 на русскомСкачать

Открытие Пенроузов

В 1958 году Британский психологический журнал опубликовал статью Л. Пенроуза и Р. Пенроуза, в которой они ввели в рассмотрение новый тип оптической иллюзии, названной ими «невозможный треугольник».

Зрительно невозможный треугольник воспринимается как реально существующая в трехмерном пространстве конструкция, составленная из прямоугольных брусков. Но это всего лишь оптическая иллюзия. Построить реальную модель невозможного треугольника нельзя.

Статья Пенроузов содержала несколько вариантов изображения невозможного треугольника. — его «классическое» представление.

Видео:Разгадка, в которую невозможно поверить: задача о 100 заключённых [Veritasium]Скачать

Из каких элементов строится невозможный треугольник?

Точнее, из каких элементов он кажется нам построенным? В основе конструкции лежит прямоугольный уголок, который получается соединением под прямым углом двух одинаковых прямоугольных брусков. Таких уголков требуется три штуки, а брусков, стало быть, шесть штук. Эти уголки надо определенным образом зрительно «соединить» один с другим так, чтобы они образовали замкнутую цепь. То, что получится, и есть невозможный треугольник.

Первый уголок поместим в горизонтальной плоскости. К нему присоединим второй уголок, направив одно из его ребер вверх. Наконец, к этому второму уголку пристроим третий уголок так, чтобы его ребро было параллельно исходной горизонтальной плоскости . При этом два ребра первого и третьего уголков будут параллельны и направлены в разные стороны.

Если считать брусок отрезком единичной длины, то концы брусков первого уголка имеют координаты , и , второго уголка — , и , третьего — , и . Мы получили реально существующую в трехмерном пространстве «закрученную» конструкцию .

А теперь попробуем мысленно посмотреть на нее из разных точек пространства . Представьте, как она выглядит из одной точки, из другой, из третьей. При изменении точки наблюдения будет казаться, что два «концевых» ребра наших уголков перемещаются относительно друг друга. Не трудно подобрать такое положение, при котором они соединятся .

Но если расстояние между ребрами намного меньше расстояния от уголков до точки, из которой мы рассматриваем нашу конструкцию, то оба ребра будут иметь для нас одинаковую толщину, и возникнет представление о том, что эти два ребра — на самом деле продолжение один другого. Такая ситуация изображена 4.

Кстати, если мы одновременно посмотрим на отражение конструкции в зеркале, то там замкнутой цепи не увидим.

А из выбранной точки наблюдения мы собственными глазами видим свершившееся чудо: имеется замкнутая цепь из трех уголков. Только не меняйте точку наблюдения, чтобы эта иллюзия не разрушилась. Теперь можно нарисовать видимый вам объект или поместить в найденную точку объектив фотоаппарата и получить фотографию невозможного объекта.

Первыми этим явлением заинтересовались Пенроузы. Они использовали возможности, которые возникают при отображении трехмерного пространства и трехмерных объектов на двумерную плоскость и обратили внимание на некоторую неопределенность проектирования — незамкнутая конструкция из трех уголков может восприниматься как замкнутая цепь.

Видео:10 Невозможных фигур. Оптические иллюзии.Скачать

Доказательство невозможности треугольника Пенроузов

Анализируя особенности двумерного изображения трехмерных объектов на плоскости, мы поняли, как особенности этого отображения приводят к невозможному треугольнику. Возможно, кого-то заинтересует и чисто математическое доказательство.

Доказать, что невозможный треугольник не существует, крайне легко, ведь каждый его угол прямой, а их сумма равна 270 градусов вместо «положенных» 180 градусов.

Более того, даже если мы будем рассматривать невозможный треугольник, склеенный из уголков, меньших 90 градусов, то в этом случае можно доказать, что невозможный треугольник не существует.

Мы видим три плоские грани . Они попарно пересекаются вдоль прямых. Плоскости, содержащие эти грани, попарно ортогональны, поэтому они пересекаются в одной точке.

Кроме того, через эту точку должны проходить линии взаимного пересечения плоскостей. Следовательно, прямые линии 1, 2, 3 должны пересекаться в одной точке.

Но это не так. Следовательно, представленная конструкция невозможна.

Видео:Удивительный парадокс! Как такое может быть? 63=64=65?Скачать

«Невозможное» искусство

Судьба той или иной идеи — научной, технической, политической — зависит от очень многих обстоятельств. И далеко не в последнюю очередь от того, в какой именно форме эта идея будет представлена, в каком образе она явится широкой публике. Будет ли воплощение сухим и сложным для восприятия, или, наоборот — явление идеи будет ярким, захватывающим наше внимание даже вопреки нашей воле.

У невозможного треугольника судьба счастливая. В 1961 г. голландский художник Мориц Эшер завершил литографию, названную им «Водопад» . Художник прошел немалый, но быстрый путь от самой идеи невозможного треугольника до ее потрясающего художественного воплощения. Напомним, статья Пенроузов появилась в 1958 году.

В основе «Водопада» — два невозможных треугольника, показанных. Один треугольник — большой, внутри него расположен другой треугольник. Может показаться, что изображены три одинаковых невозможных треугольника. Но не в этом суть, представленная конструкция достаточно сложная.

При беглом взгляде ее абсурдность не всякому и не сразу будет видна, так как каждое соединение, представленное , — возможно. как говорят, локально, то есть на небольшом участке чертежа, такая конструкция осуществима… Но в целом она невозможна! Ее отдельные куски не стыкуются, не согласуются друг с другом.

А чтобы понять это, мы должны затратить определенные интеллектуальные и зрительные усилия.

Давайте совершим путешествие по граням конструкции. Этот путь замечателен тем, что вдоль него, как нам кажется , уровень относительно горизонтальной плоскости остается неизменным. Двигаясь вдоль этого пути, мы ни вверх не поднимаемся, ни вниз не опускаемся.

И все-то было бы хорошо, привычно, если бы в конце пути — а именно в точке — мы не обнаружили бы, что относительно исходной, начальной точки мы каким-то таинственным немыслимым образом поднялись вверх по вертикали!

Чтобы прийти к этому парадоксальному результату, мы должны выбрать именно этот путь, да еще следить за уровнем относительно горизонтальной плоскости… Непростая задача. В ее решении Эшеру на помощь пришла…вода. Вспомним песню о движении из чудесного вокального цикла Франца Шуберта «Прекрасная Мельничиха»:

И сначала в воображении, а затем под рукой замечательного мастера голые и сухие конструкции превращаются в акведуки , по которым бегут чистые и быстрые потоки воды. Их движение захватывает наш взгляд, и вот уже помимо нашей воли мы устремляемся по течению, следуя всем поворотам и изгибам пути, вместе с потоком срываемся вниз, падаем на лопасти водяной мельницы, затем снова устремляемся вниз по течению…

Обходим этот путь раз, другой, третий… и только тут осознаем: двигаясь в н и з, мы каким-то фантастическим образом подымаемся в в е р х! Первоначальное удивление перерастает в некий интеллектуальный дискомфорт. Кажется, что мы стали жертвой какого-то розыгрыша, объектом какой-то шутки, которую пока еще не поняли.

И снова мы повторяем этот путь по странному водоводу, теперь уже не спеша, с осторожностью, словно опасаясь подвоха со стороны парадоксальной картинки, критически воспринимая все то, что происходит на этом таинственном пути.

Мы пытаемся разгадать ту тайну, которая поразила нас, и не можем вырваться из ее плена до тех пор, пока не найдем скрытую пружину, лежащую в ее основе и приводящую немыслимую круговерть в безостановочное движение.

Художник специально подчеркивают, навязывает нам восприятие его картины как изображения реальных трехмерных объектов. Объемность подчеркивается изображением вполне реальных многогранников на башнях, кирпичной кладкой с аккуратнейшим представлением каждого кирпича в стенах акведука, поднимающимися вверх террасами с садами на заднем плане. Все призвано убедить зрителя в реальности происходящего. И благодаря искусству и великолепной технике эта цель достигнута.

Когда же мы вырываемся из плена, в который попадает наше сознание, начинаем сравнивать, сопоставлять, анализировать, то находим что основа, источник этой картины скрыты в особенностях проектирования.

И мы получили еще одно — «физическое» доказательство невозможности «невозможного треугольника»: если бы такой треугольник существовал, то существовал бы и «Водопад» Эшера, который есть по сути дела вечный двигатель. Но вечный двигатель невозможен, следовательно, невозможен и «невозможный треугольник». И, наверное, это «доказательство» — самое убедительное.

Что сделало Морица Эшера феноменом, уникумом, который не имел в искусстве явных предшественников и которому невозможно подражать? Это комбинация плоскостей и объемов, пристальное внимание к причудливым формам микромира — живого и неживого, к необычным точкам зрения на обычные вещи. Основной эффект его композиций — эффект появления невозможных отношений между знакомыми предметами. Эти ситуации с первого взгляда могут и напугать, и вызвать улыбку. Можно радостно смотреть на забаву, которую предлагают художник, а можно серьезно погрузиться в глубины диалектики.

Мориц Эшер показал, что мир может быть совсем не таким, каким мы его видим и привыкли воспринимать — надо только посмотреть на него под другим, новым углом зрения!

Видео:ЗАНИМАТЕЛЬНАЯ ГЕОМЕТРИЯ. ПАРАДОКСЫ ТРЕУГОЛЬНИКОВ.Скачать

Мориц Эшер

Морицу Эшеру более повезло как ученому, чем как художнику. В его гравюрах и литографиях видели ключи к доказательству теорем или оригинальные контрпримеры, бросающие вызов здравому смыслу. На худой конец их воспринимали как прекрасные иллюстрации к научным трактатам по кристаллографии, теории групп, когнитивной психологии или компьютерной графике. Мориц Эшер работал в области соотношений пространства, времени и их тождественности, использовал базовые образцы мозаик, применяя к ним трансформации. Это великий мастер оптических обманов. Гравюры Эшера изображают не мир формул, а красоту мира. Их интеллектуальный склад коренным образом противоположен алогичным творениям сюрреалистов.

Голландский художник Мориц Корнелиус Эшер родился 17 июня 1898 года в провинции Голландии. В доме, котором родился Эшер, сейчас находится музей.

С 1907 года Мориц учится плотницкому делу и игре на пианино, обучается в средней школе. Оценки по всем предметам у Морица были плохими за исключением рисования. Учитель рисования заметил талант у мальчика и научил его делать гравюры по дереву.

В 1916 году Эшер выполняет свою первую графическую работу, гравюру на фиолетовом линолеуме — портрет своего отца Г. А. Эшера. Он посещает мастерскую художника Герта Стигемана, имевшего печатный станок. На этом станке были отпечатаны первые гравюры Эшера.

В 1918-1919 годах Эшер посещает Технический колледж в голландском городке Дельфт. Он получает отсрочку от службы в армии для продолжения учебы, но из-за плохого здоровья Мориц не справился с учебным планом, и был отчислен. В результате, он так и не получил высшего образования. Он учится в Школе архитектуры и орнамента в городе Гаарлеме, Там он берет уроки рисования у Самюэля Джесерена де Месквита, оказавшего формирующее влияние на жизнь и творчество Эшера.

В 1921 году семья Эшера посетила Ривьеру и Италию. Очарованный растительностью и цветами средиземноморского климата, Мориц сделал детальные рисунки кактусов и оливковых деревьев. Он зарисовал много эскизов горных пейзажей, которые позже легли в основу его работ. Позже он будет постоянно возвращаться в Италию, которая будет служить для него источником вдохновения.

Эшер начинает экспериментировать в новом для себя направлении, уже тогда в его работах встречаются зеркальные отображения, кристаллические фигуры и сферы.

Конец двадцатых годов оказалась очень плодотворным периодом для Морица. Его работы демонстрировались на многих выставках Голландии, а к 1929 году его популярность достигла такого уровня, что за один год прошли пять персональных выставок в Голландии и Швейцарии. Именно в этот период картины Эшера впервые были названы механическими и «логическими».

Эшер много путешествует. Живет в Италии и Швейцарии, Бельгии. Изучает мавританские мозаики, делает литографии, гравюры. На основе эскизов путешествий он создает свою первую картину невозможной реальности Still Life with Street.

В конце тридцатых годов Эшер продолжает эксперименты с мозаиками и трансформациями. Он создает мозаику в виде двух птиц, летящих навстречу друг другу, которая легла в основу картины «День и ночь».

В мае 1940 года нацисты оккупируют Голландию и Бельгию, а 17 мая в зону оккупации попадает и Брюссель, где на тот момент проживал Эшер с семьей. Они находят дом в Варне и переезжают туда в феврале 1941 года. До конца своих дней Эшер будет жить в этом городе.

В 1946 году Эшер начинает интересоваться технологией глубокой печати. И хотя эта технология была намного сложнее той, которой пользовался Эшер до этого и требовала больше времени для создания картины, но результаты были впечатляющими — тонкие линии и точная передача теней. Одна из самых известный работ в технике глубокой печати «Капля росы» была закончена в 1948 году.

В 1950 году Мориц Эшер обретает популярность как лектор. Тогда же в 1950 году проходит его первая персональная выставка в Соединенных Штатах и начинают покупаться его работы. 27 апреля 1955 года Морица Эшера посвящают в рыцари и он становится дворянином.

В середине 50-х годов Эшер объединяет мозаику с фигурами, уходящими в бесконечность.

В начале 60-х годов вышла в свет первая книга с работами Эшера «Grafiek en Tekeningen», в которой 76 работ прокомментировал сам автор. Книга помогла обрести понимание среди математиков и кристаллографов, включая некоторых из России и Канады.

В августе 1960 Эшер прочитал лекцию по кристаллографии в Кембридже. Математические и кристаллографические аспекты творчества Эшера становятся очень популярными.

В 1970 году после новой серии операций Эшер переехал в новый дом в Ларене , в котором была студия, но плохое здоровье не давало возможности много работать.

В 1971 году Мориц Эшер скончался в возрасте 73 лет. Эшер прожил достаточно долго, чтобы увидеть книгу «Мир М. К. Эшера», переведенную на английский язык и остался ею очень доволен.

Различные невозможные картины встречаются на сайтах математиков и программистов. Самой полной версией из просмотренных нами, на наш взгляд, является сайт Влада Алексеева

На этом сайте представлены не только широко известные картины, в том числе и М. Эшера, но, и анимированные изображения, забавные рисунки невозможных животных, монет, марок и т.п. Этот сайт живет, он периодически обновляется и пополняется удивительными рисунками.

📸 Видео

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Геометрический софизм ➄ Парадоксы в математикеСкачать

Задача, которую исключили из экзамена в АмерикеСкачать

Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Парадокс Бертрана – что не так со случайностью // Vital MathСкачать

Парадокс: 5=7. Доказательство, с которыми не поспоришьСкачать

парадоксСкачать

РЕШЕНИЕ ПАРАДОКСА ТРЕУГОЛЬНИКОВСкачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

мой способ вычисления площади круга, парадокс треугольникаСкачать