Орт вектора и оси

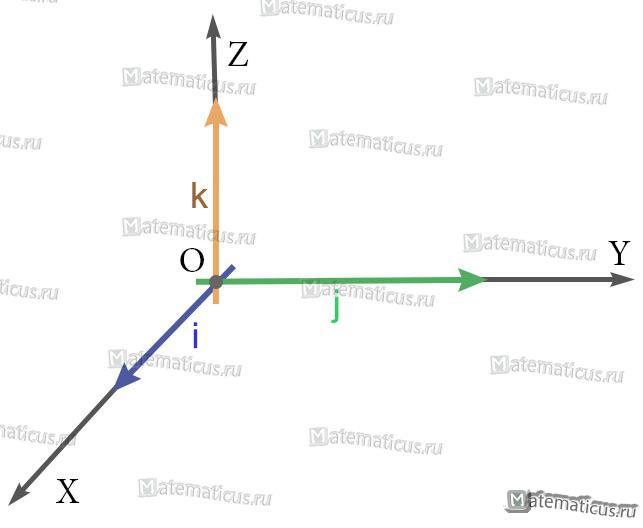
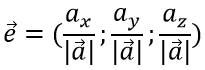Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.

i — единичный вектор оси абсцисс;

j — единичный вектор оси ординат;

k — единичный вектор оси аппликат.

i⊥j⊥k, i=j=k=1

В прямоугольной системе координат в пространстве координаты векторов равны:

i(1;0;0), j(0;1;0), k(0;0;1)

Единичные векторы являются некомпланарными.

Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.

a=xi+уj+zk

где x, y, z — координаты вектора проекции на соответствующие координатные оси.

Эта формула называется разложением вектора по ортам координатных осей.

Единичный вектор определяется по формуле:

Дан вектор а = (1; 2; -2)

Требуется найти длину (модуль) и единичный вектор e направления вектора а

Находим длину вектора a

затем вычисляем единичный вектор e

Видео:#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

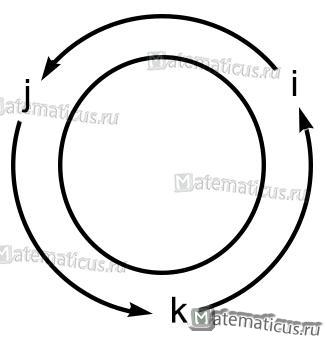
Векторное произведения единичных векторов

Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.

На основании схемы получаем таблицу векторного произведения единичных векторов

Пример 1
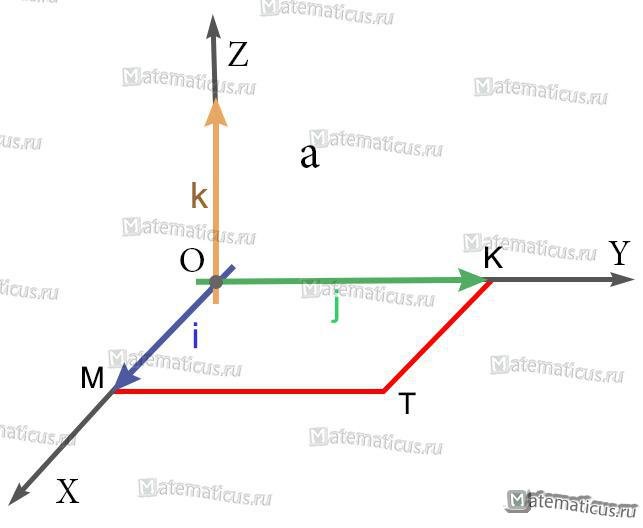
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.

Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).

iхj=k

Пример 2
Найти векторное произведение jхi.

Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.5 / 5. Количество оценок: 4

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Что такое орты

Орт:

• это вектор,
• он лежит на оси,
• направлен туда же, куда направлена ось,
• его длина равна единице.

На рисунке 1 изображены орты для двумерного а) и трехмерного б) случаев.

Орты сонаправлены с осями, на которых они лежат:

• Орт ( vec ) направлен вдоль оси Ox;
• Орт ( vec ) направлен вдоль оси Oy;
• Орт ( vec ) направлен вдоль оси Oz;

Орты обладают единичной длиной:

Все три орта взаимно перпендикулярны. Перпендикулярные векторы часто называют ортогональными.

Любые два орта из трех, лежат в одной плоскости:

• Орты ( vec ) и ( vec ) лежат в плоскости xOy;
• Орты ( vec ) и ( vec ) лежат в плоскости xOz;
• Орты ( vec ) и ( vec ) лежат в плоскости yOz;

Векторы, лежащие в одной плоскости, называют компланарными. Об этом подробно написано «здесь» (откроется в новой вкладке).

Координаты вектора можно указать двумя способами. Либо, перечислив эти координаты в скобках, либо, с помощью разложения вектора по ортам.

Видео:2 37 Нахождение орта вектораСкачать

Как найти орт вектора

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Формула

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Примеры нахождения орта вектора

Задание. На плоскости задан вектор $bar=(-2 ; 2)$ . Найти его орт.

Решение. Для нахождения орта заданного вектора воспользуемся формулой:

Подставляя заданные координаты, получим:

Задание. Даны точки $A(3 ;-1 ; 4)$ и $B(2 ; 0 ; 2)$ . Найти орт вектора $overline$

Решение. Найдем координаты вектора $overline$, для этого из координат конца вектора (точки $B$ ) вычтем соответствующие координаты начала (точки $A$ ):

Для нахождения орта полученного вектора воспользуемся формулой

Подставим в неё координаты вектора $overline$, будем иметь:

Таким образом, орт вектора $overline$ имеет координаты $bar=left(-frac<sqrt> ; frac<sqrt> ;-frac<sqrt>right)$

💥 Видео

Единичный векторСкачать

§7 Направляющие косинусы вектораСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

§4 Проекция вектора на осьСкачать

Угол между векторами | МатематикаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Координаты вектора в пространстве. 11 класс.Скачать

Построение проекции вектора на осьСкачать

Координаты вектора. 9 класс.Скачать

Урок 9. Проекции вектора на координатные осиСкачать

Линейная алгебра. Векторы и операции над векторами.Скачать

Проекция вектора на вектор.Скачать

Координаты точки и координаты вектора 1.Скачать