Определи вид четырехугольника pp1q1q и рассчитай его периметр (5 видео)

Как найти периметр сторон четырехугольника, формула нахождения

Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.

Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.

Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.

Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме. С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.

Содержание

Школьное задание
124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках P1и Q1. Докажите, что PQ = P1Q1.
124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках P1и Q1. Докажите, что PQ = P1Q1.
Презентация на тему Перпендикулярные прямые в пространстве
Слайды и текст этой презентации
📹 Видео

Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Школьное задание

Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?

Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».

Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.

Вопросы:

Что такое «периметр»?
Как находить периметр четырехугольника?

Ответы на вопросы:

Для тех, кто знает, вспоминаем, а кто не знает — объясняем:

Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.

Решение:

В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.

2+2+3+3=10

Как мы видим, периметр нашей четырехугольной фигуры равен 10.

В математике сумму всех сторон (периметр) мы обозначаем символом Р.

Теперь записываем правильное решение этой задачи:

Р=2+2+3+3;

Ответ: Р=10.

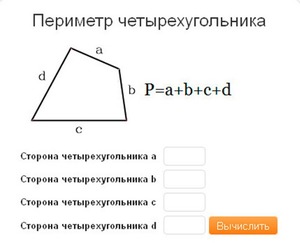
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:

P = a + b + c + d (где a , b, c, d являются границами четырехугольника).

Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.

Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.

Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.

На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.

Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.

Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.

В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках P1и Q1. Докажите, что PQ = P1Q1.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках P₁и Q₁. Докажите, что PQ = P₁Q₁.

PP₁ || Q₁Q, как перпендикулярные одной плоскости.

Следовательно, РР₁ и QQ₁ принадлежат одной плоскости. Назовем ее β. Пусть P₁Q₁ — линия пересечения плоскостей α и β.

Таким образом, PQQ₁P₁ — параллелограмм, следовательно, PQ =

Что и требовалось доказать.

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №124
к главе «Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости».

Видео:Описанные четырехугольники. 9 класс.Скачать

Презентация на тему Перпендикулярные прямые в пространстве

Презентация на тему Презентация на тему Перпендикулярные прямые в пространстве, предмет презентации: Математика. Этот материал содержит 27 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!

Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Слайды и текст этой презентации

«Перпендикулярные прямые в пространстве»

«Параллельные прямые, перпендикулярные к плоскости».
«Перпендикулярность прямой и плоскости»

Ввести понятие перпендикулярных прямых в пространстве;
Доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой;
Дать определение перпендикулярности прямой и плоскости;
Доказать теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярности к плоскости.

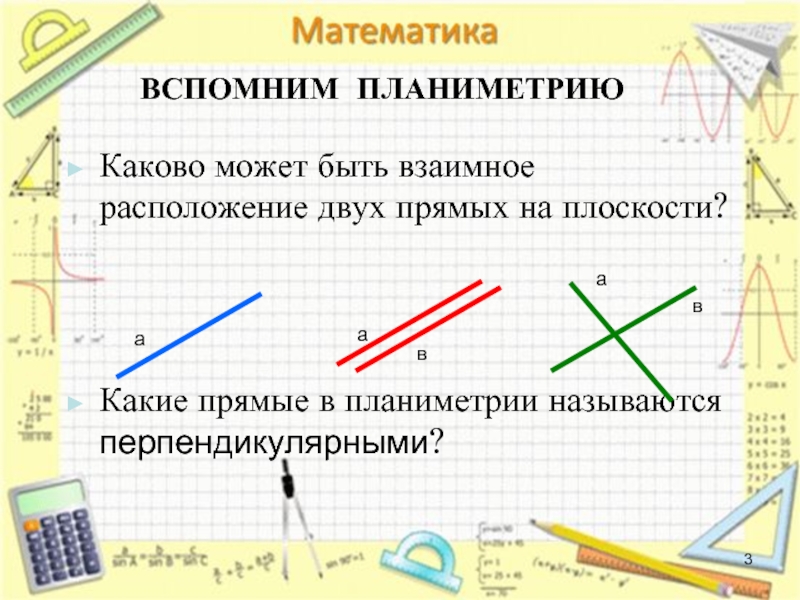
Каково может быть взаимное расположение двух прямых на плоскости?

Какие прямые в планиметрии называются перпендикулярными?

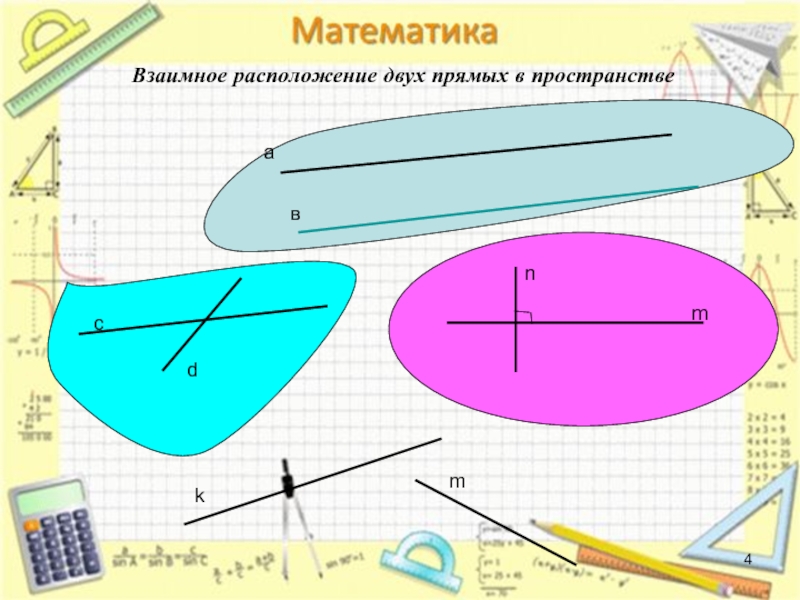
Взаимное расположение двух прямых в пространстве

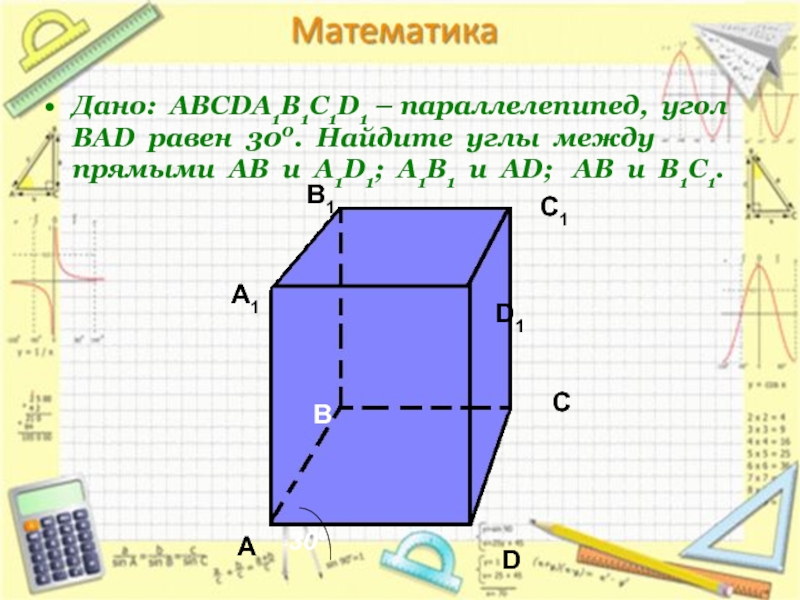
Дано: АВСDA1B1C1D1 – параллелепипед, угол ВАD равен 300. Найдите углы между прямыми АВ и А1D1; А1В1 и АD; АВ и В1С1.

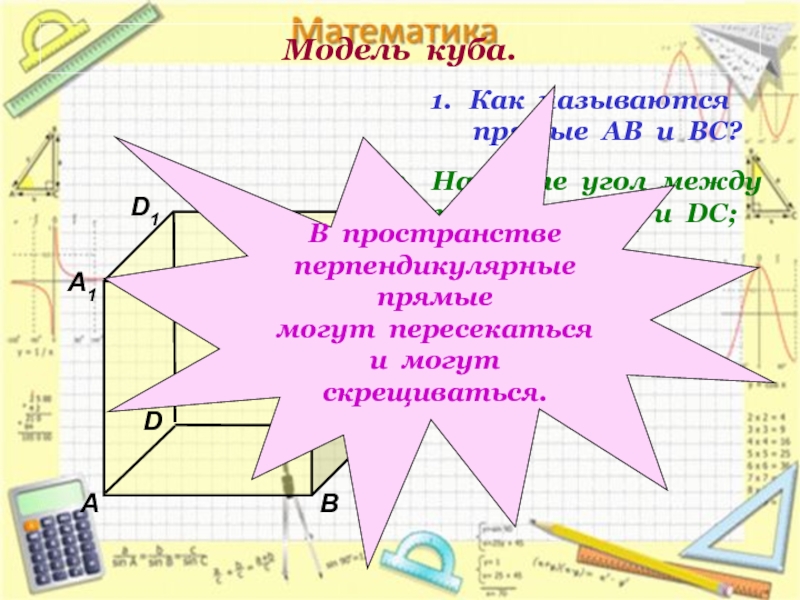
Как называются
прямые АВ и ВС?

Найдите угол между
прямыми АА1 и DC;
ВВ1 и АD.

В пространстве
перпендикулярные прямые
могут пересекаться
и могут скрещиваться.

Перпендикулярные прямые в пространстве

Две прямые в пространстве
называются перпендикулярными
(взаимно перпендикулярными),
если угол между ними равен 90°.
Обозначается a ┴ b
Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

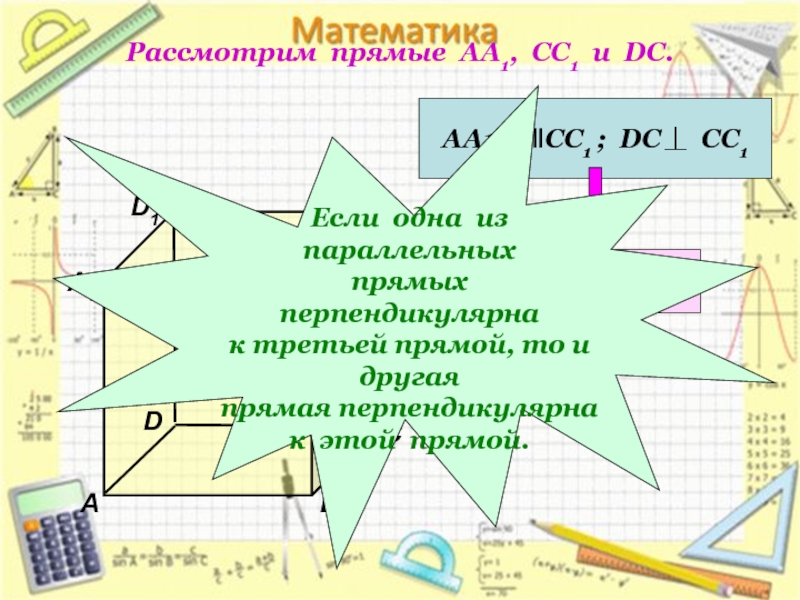
Рассмотрим прямые АА1, СС1 и DC.

АА1 ‌ ‌ ǁСС1 ; DC СС1

Если одна из параллельных
прямых перпендикулярна
к третьей прямой, то и другая
прямая перпендикулярна
к этой прямой.

1. Если плоскость перпендикулярна одной
из двух параллельных прямых,
то она перпендикулярна другой
прямой. (a ⊥ α b и a II b => b ⊥ α)

2. Если две прямые перпендикулярны
одной и той же плоскости,
то они параллельны. (a ⊥ α и b ⊥ α => a II b)

3. Если прямая перпендикулярна
одной из двух параллельных
плоскостей, то она перпендикулярна
и другой плоскости. (α II β и a ⊥ α => a ⊥ β)

4. Если две различные плоскости
перпендикулярны одной и той же прямой,
то эти плоскости параллельны.
(a ⊥ α и a ⊥ β => a II β)

5. Через любую точку пространства можно
провести прямую, перпендикулярную
данной плоскости, и притом только одну.

6. Через любую точку прямой можно
провести плоскость, перпендикулярную ей
и притом только одну.

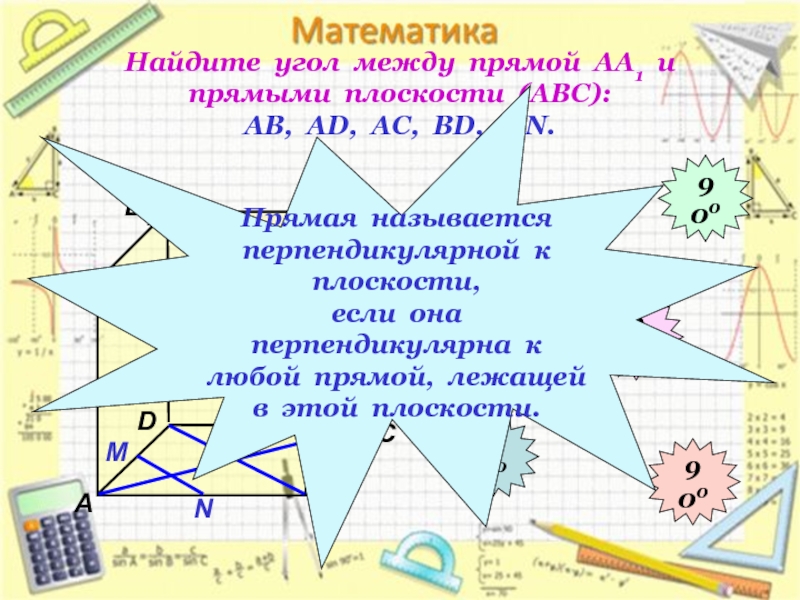
Найдите угол между прямой АА1 и прямыми плоскости (АВС): АВ, АD, АС, ВD, МN.

Прямая называется
перпендикулярной к плоскости,
если она перпендикулярна к
любой прямой, лежащей
в этой плоскости.

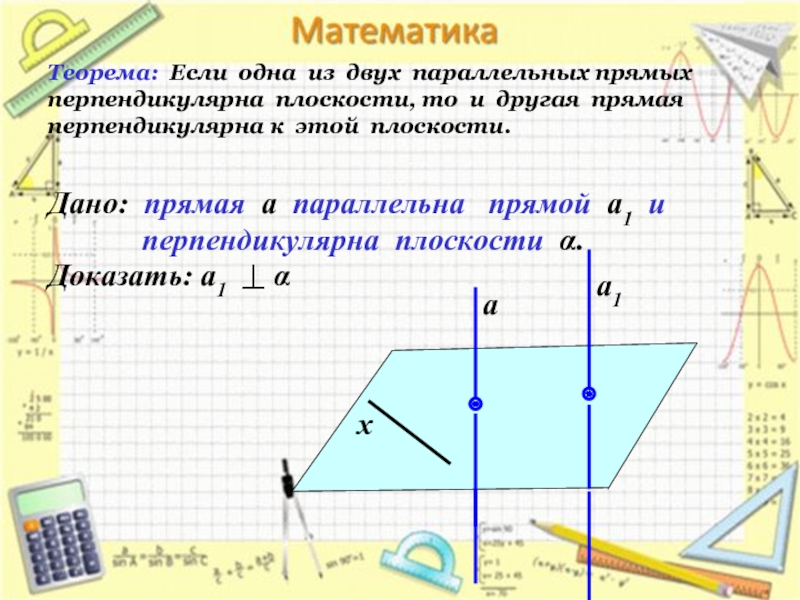
Теорема: Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости.

Дано: прямая а параллельна прямой а1 и
перпендикулярна плоскости α.
Доказать: а1 α

Проведем прямую х в плоскости α. Так как а⊥α, то а⊥х. По лемме о перпендикулярности двух параллельных прямых к третьей а ⊥х. Т.о., прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α, т.е. а ⊥α.

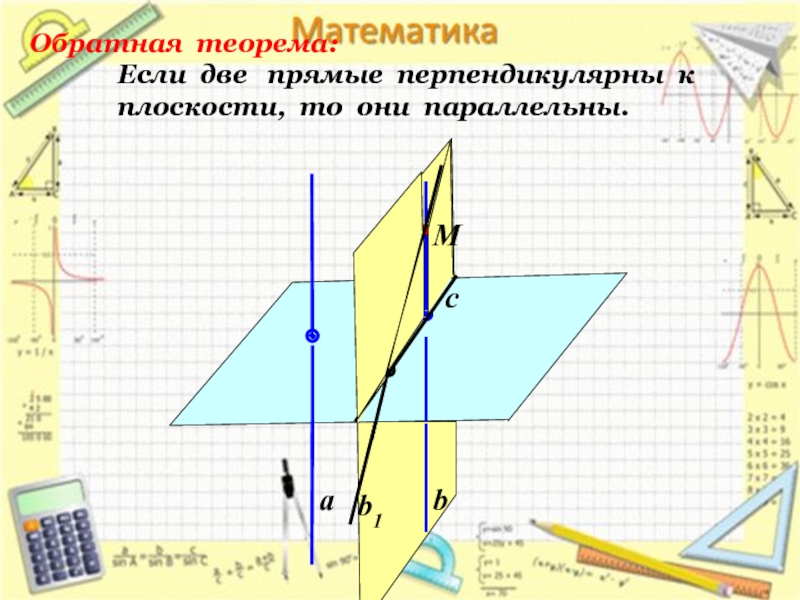
Обратная теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.

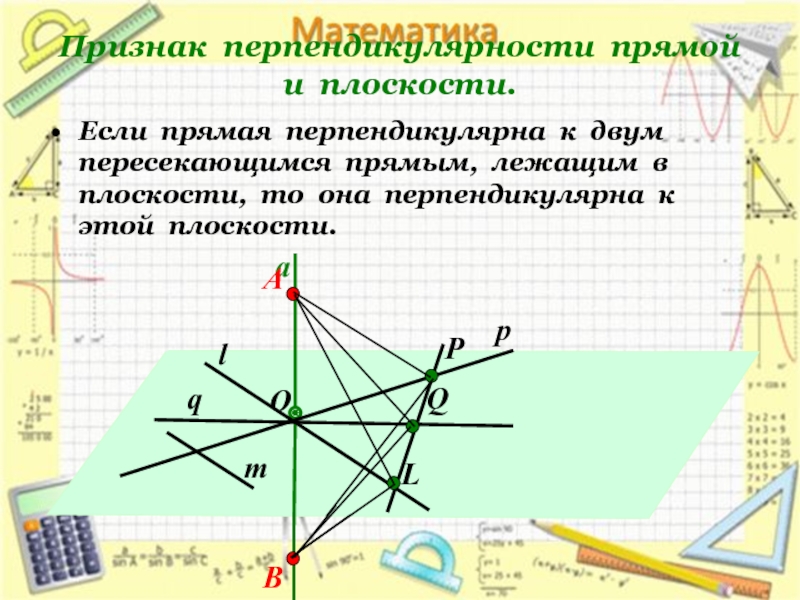
Признак перпендикулярности прямой и плоскости.

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

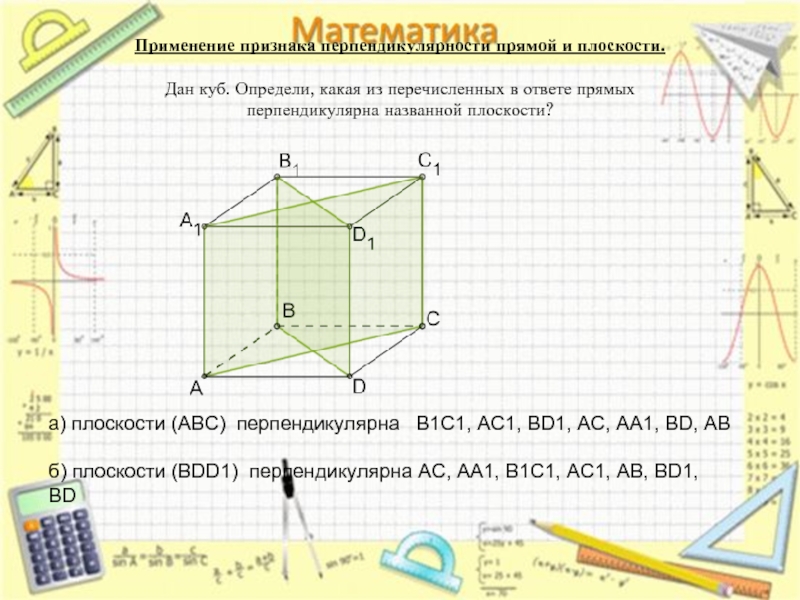
Применение признака перпендикулярности прямой и плоскости. Дан куб. Определи, какая из перечисленных в ответе прямых перпендикулярна названной плоскости?

а) плоскости (ABC) перпендикулярна B1C1, AC1, BD1, AC, AA1, BD, AB

б) плоскости (BDD1) перпендикулярна AC, AA1, B1C1, AC1, AB, BD1, BD

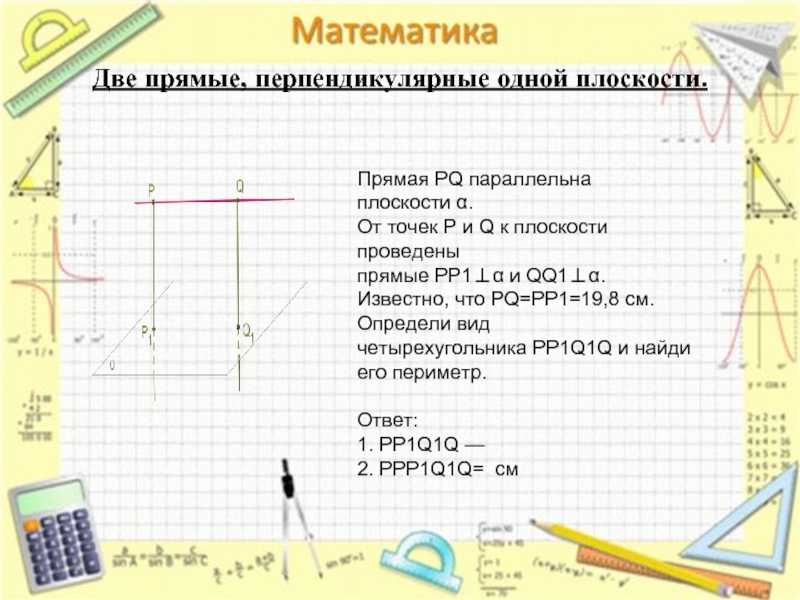
Две прямые, перпендикулярные одной плоскости.

Прямая PQ параллельна плоскости α.
От точек P и Q к плоскости проведены прямые PP1⊥α и QQ1⊥α. Известно, что PQ=PP1=19,8 см.
Определи вид четырехугольника PP1Q1Q и найди его периметр.

Ответ:
1. PP1Q1Q —
2. PPP1Q1Q= см

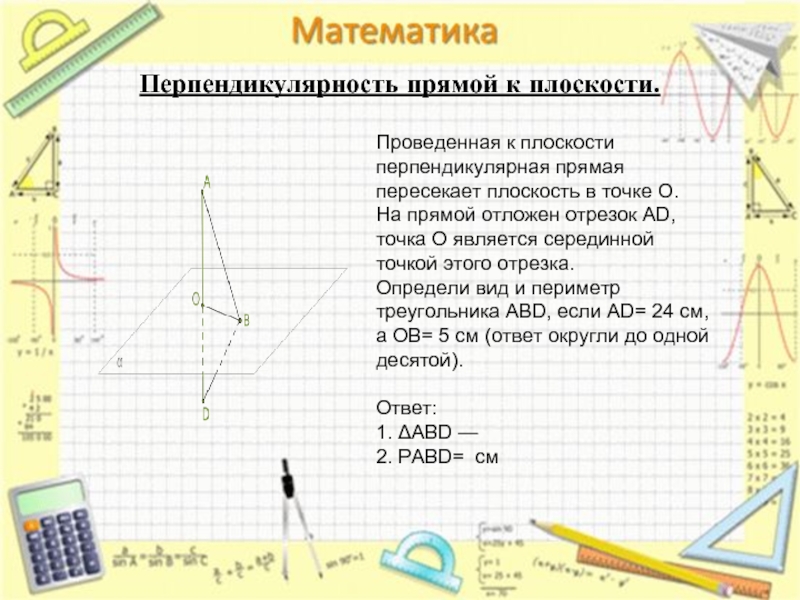
Перпендикулярность прямой к плоскости.

Проведенная к плоскости перпендикулярная прямая пересекает плоскость в точке O.
На прямой отложен отрезок AD, точка O является серединной точкой этого отрезка.
Определи вид и периметр треугольника ABD, если AD= 24 см, а OB= 5 см (ответ округли до одной десятой).

Ответ:
1. ΔABD —
2. PABD= см

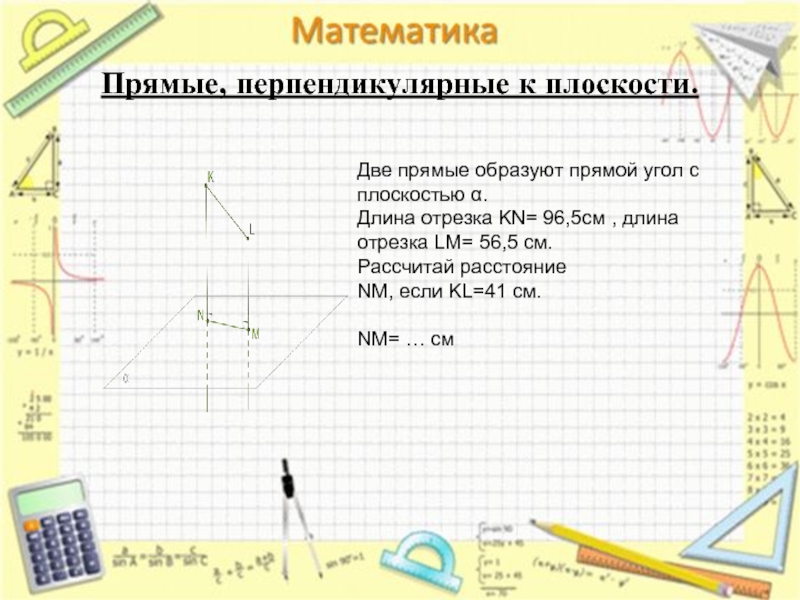
Прямые, перпендикулярные к плоскости.

Две прямые образуют прямой угол с плоскостью α.
Длина отрезка KN= 96,5cм , длина отрезка LM= 56,5 см.
Рассчитай расстояние NM, если KL=41 см.

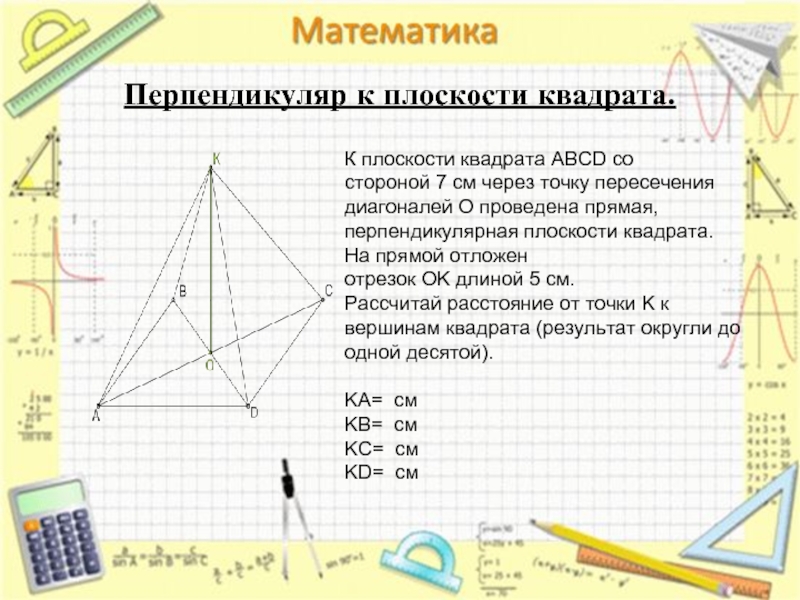
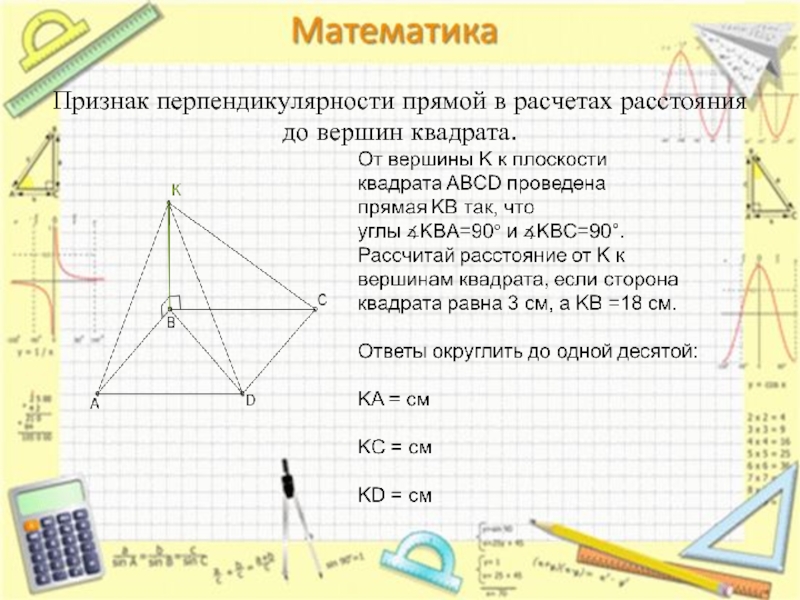
Перпендикуляр к плоскости квадрата.

К плоскости квадрата ABCD со стороной 7 см через точку пересечения диагоналей O проведена прямая, перпендикулярная плоскости квадрата.
На прямой отложен отрезок OK длиной 5 см.
Рассчитай расстояние от точки K к вершинам квадрата (результат округли до одной десятой).

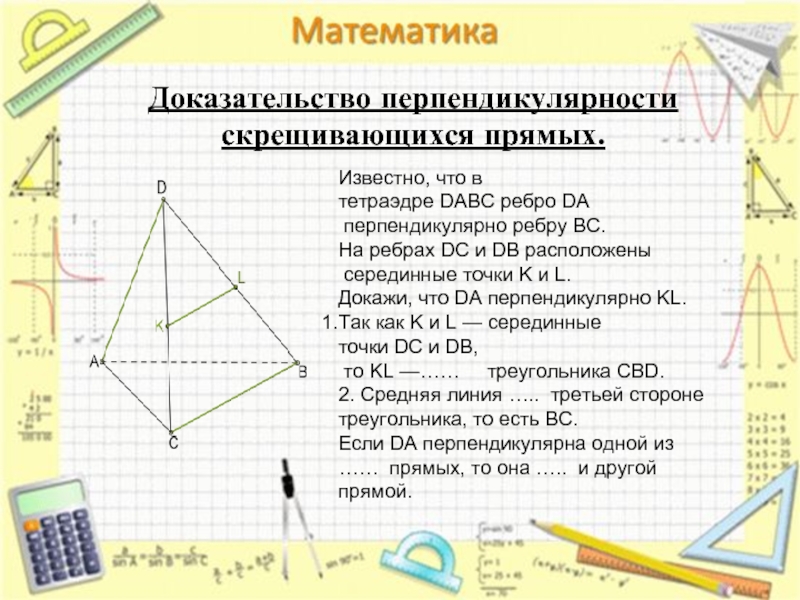
Доказательство перпендикулярности скрещивающихся прямых.

Известно, что в тетраэдре DABC ребро DA
перпендикулярно ребру BC.
На ребрах DC и DB расположены
серединные точки K и L.
Докажи, что DA перпендикулярно KL.
Так как K и L — серединные точки DC и DB,
то KL —…… треугольника CBD.
2. Средняя линия ….. третьей стороне треугольника, то есть BC.
Если DA перпендикулярна одной из …… прямых, то она ….. и другой прямой.

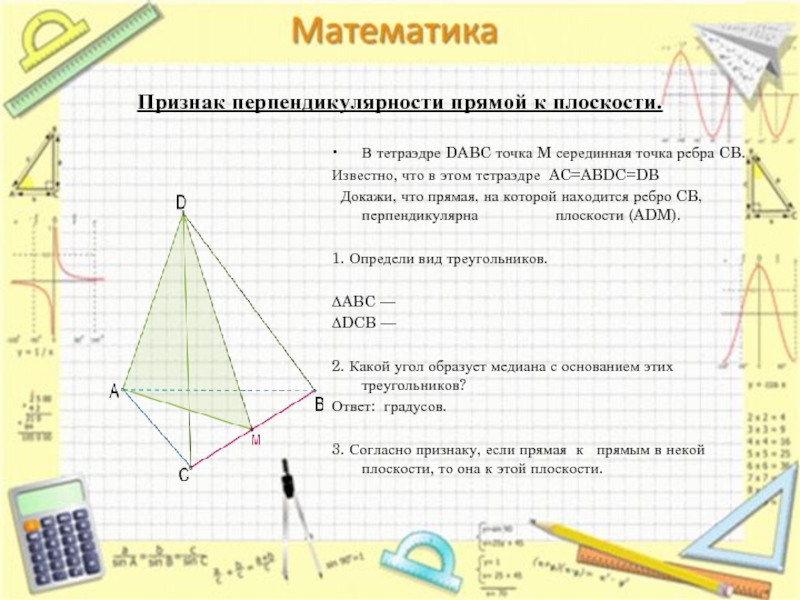
Признак перпендикулярности прямой к плоскости.

В тетраэдре DABC точка M серединная точка ребра CB.
Известно, что в этом тетраэдре AC=ABDC=DB
Докажи, что прямая, на которой находится ребро CB, перпендикулярна плоскости (ADM).

1. Определи вид треугольников.

2. Какой угол образует медиана с основанием этих треугольников?
Ответ: градусов.

3. Согласно признаку, если прямая к прямым в некой плоскости, то она к этой плоскости.

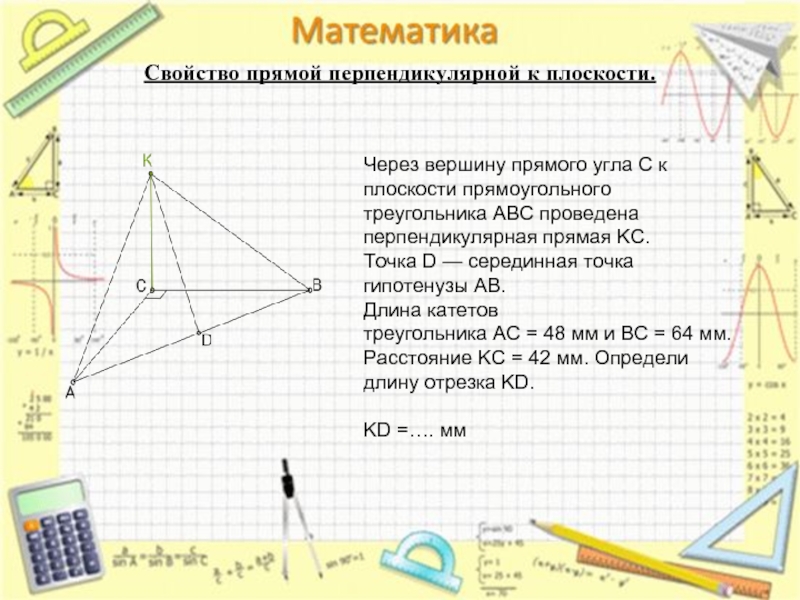
Свойство прямой перпендикулярной к плоскости.

Через вершину прямого угла C к плоскости прямоугольного треугольника ABC проведена перпендикулярная прямая KC.
Точка D — серединная точка гипотенузы AB.
Длина катетов треугольника AC = 48 мм и BC = 64 мм.
Расстояние KC = 42 мм. Определи длину отрезка KD.

(сложное) Доказательство от противного.

Прямая d перпендикулярна плоскости α и прямой m, которая не лежит в плоскости α.
Докажи, что прямая m параллельна плоскости α.

1. Согласно данной информации, если прямая не лежит в плоскости, она может или быть …плоскости, или … плоскость.
2. Допустим, что прямая m не …. а …..плоскость α.
3. Если прямая d по данной информации перпендикулярна плоскости α, то она …… каждой прямой в этой плоскости, в том числе и прямой, которая проведена через точки, в которых плоскость пересекает прямые d и m.
4. Мы имеем ситуацию, когда через одну точку к прямой d проведены две …… прямые.
5. Это противоречие, из чего следует, что прямая m….. плоскости α, что и требовалось доказать.