Диагонали четырехугольника равны 8 и 4. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Это задание ещё не решено, приводим решение прототипа.
Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно,
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Найти периметр четырехугольника вершинами которого являются середины сторон ромба 8 и 12
БАЗА ЗАДАНИЙ
Задание № 3. Планиметрия.
95. Найдите высоту ромба, сторона которого равна √3, а острый угол равен 60°.
96. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
97. Найдите большую диагональ ромба, сторона которого равна √3, а острый угол равен 60°.
98. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
99. В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60°. Найдите ее периметр.
100. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
101. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
102. Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.
103. Основания трапеции относятся как 2:3, а средняя линия равна 5. Найдите меньшее основание.
104. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
105. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
106. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
107. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50°? Ответ дайте в градусах
108. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
109. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
110. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
111. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
112. В трапеции АВСD основание AB равно 10. Средняя линии EF пересекается с диагональю BD в точке О. Разность отрезков ЕО и OF равна 3. Найдите среднюю линию EF.
113. Основания равнобедренной трапеции равны 5 и 17, а ее периметр равен 42. Найдите площадь трапеции.
114. Основания равнобедренной трапеции равны 10 и 40. Боковые стороны равны 25. Найдите косинус острого угла трапеции.
115. Найдите площадь прямоугольной трапеции, основания которой равны 7 и 3, большая боковая сторона составляет с основанием угол 45°.
116. Радиус окружности, вписанной в правильный треугольник равен 2/√3. Найдите сторону этого треугольника.
117. Периметр треугольника равен 70, а радиус вписанной окружности равен 4. Найдите площадь этого треугольника.
118. Сторона ромба равна 1, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
120 Периметр правильного шестиугольника равен 30. Найдите диаметр описанной окружности.
121. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен √3.
122. Найдите сумму углов выпуклого семиугольника. Ответ дайте в градусах.
123. Угол между двумя соседними сторонами правильного многоугольника равен 168°. Найдите число вершин многоугольника. (без рисунка)
124. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
125. Площадь круга равна 1/π. Найдите длину его окружности.
126. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
127. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
128. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
129. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
130. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
131. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
132. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
133. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.
134. Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружности, вписанной в этот треугольник.
135. Боковые стороны равнобедренного треугольника равны 5, основание 6. Найдите радиус вписанной окружности.
136. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
137. В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
138. В треугольнике ABC угол A равен 44°, угол С равен 62°. На продолжении стороны AB за точку B отложен отрезок BD, равный стороне BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.
Видео:ЕГЭ Математика Задание 6#27845Скачать

Геометрия. 8 класс
Выберите верные утверждения.
Средняя линия треугольника соединяет его вершину и середину противоположной стороны.
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника.
Средняя линия трапеции равна полусумме её оснований.
Средняя линия треугольника параллельна одной из сторон треугольника и равна половине этой стороны.
Середины сторон четырёхугольника являются вершинами ромба.
Середины сторон ромба являются вершинами прямоугольника.
Впишите правильный ответ.
В треугольнике NKP: A – середина NK, B – середина KP, C – середина NP. Найдите периметр треугольника NKP, если AB = 7 см, BC = 9 см, AC = 12 см. Ответ дайте в сантиметрах.
Установите соответствие между фигурой и её периметром.
Диагонали параллелограмма равны 23 см и 27 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон параллелограмма.
Диагональ прямоугольника равна 20 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон прямоугольника.
Диагонали ромба равны 24 см и 36 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон ромба.
💥 Видео
Геометрия Вершинами четырехугольника являются середины сторон ромба с диагоналями 8 см и 14 смСкачать

№564. Дан треугольник, стороны которого равны 8 см, 5 см и 7 см. Найдите периметр треугольника,Скачать

Диагонали четырехугольника равны 4 и 5.Скачать

№494. Найдите диагональ и площадь ромба, если его сторона равна 10 см, а другая диагональ — 12 см.Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрия Вершины четырехугольника являются середины сторон прямоугольника с диагональю 12 смСкачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

ЕГЭ 2017 | Задание 3 | Диагонали четырехугольника равны ... ✘ Школа ПифагораСкачать

Геометрия Диагонали четырехугольника равны 7 и 10. Найдите периметр четырехугольника, вершинамиСкачать

Сложные примеры с поиском периметра 3 задание проф. ЕГЭ по математикеСкачать

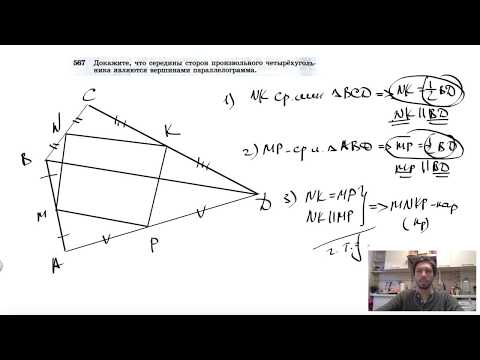
№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
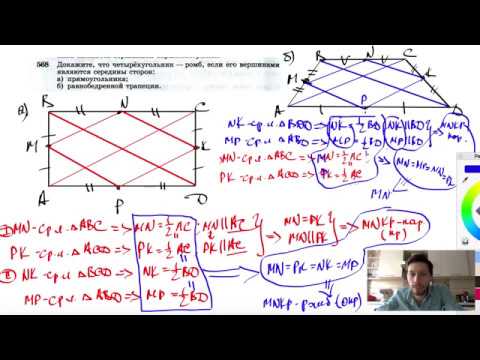
№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать
В-3 № 1-100 - Геометрия 8 класс Мерзляк дидактические материалыСкачать

Геометрия Сумма диагоналей четырехугольника равна 28 см. Найдите периметр четырехугольника, вершиныСкачать

Найти площадь параллелограмма, вершинами которого являются середины сторон данного параллелограмма.Скачать

Задание 3 (бывшее 4). Подготовка к ЕГЭ по математикеСкачать

38. Геометрия на ЕГЭ по математике. Задача на тему "Средняя линия треугольника"Скачать



































