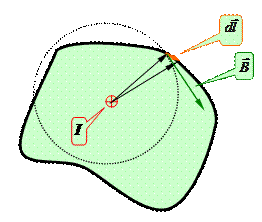
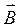
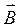
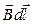
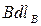
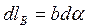
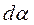
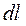
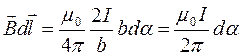
Ротор вектор магнитной индукции (2 видео)

Ротор магнитного поля

Циркуляция вектора наиболее просто вычисляется в случае прямого тока. Рассмотрим замкнутый контур, лежащий в плоскости, перпендикулярной к току. В каждой точке контура направлен по касательной к окружности с центром в месте прохождения тока и проходящей через данную точку. В выражении для циркуляции заменим на . Учтем, что — угол, на который поворачивается радиальная прямая при перемещении вдоль контура на . Таким образом,

(18.43)

Тогда для циркуляции получаем

(18.44)

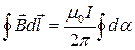
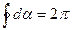
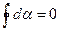
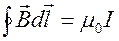
Если рассматриваемый контур охватывает ток, то при обходе по контуру радиальная прямая поворачивается в одном направлении и . Если же контур не охватывает тока, то . Поэтому можно записать:

(18.45)

где под I подразумевается ток, охватываемый контуром.

В выражении (18.45) ток рассматривается как алгебраическая величина: если направление обхода контура образует с направлением тока правовинтовую систему, то ток считают положительным, в противном случае — отрицательным.

Формула (18.45) получена для прямого тока. Но можно доказать, что онасправедлива и в общем случае, для тока произвольной формы.

Представим, что некоторый контур охватывает не один а несколько токов. Для каждого из них справедливо соотношение (18.45). В соответствии с принципом суперпозиции индукция результирующего поля равна векторной сумме полей каждого из этих токов. Поэтому циркуляция вектора индукции результирующего поля (18.46)

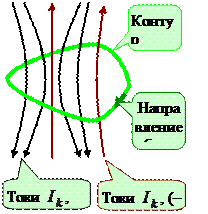
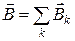
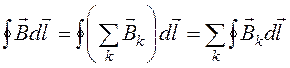
По формуле (18.45)

(18.47)

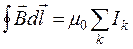
Важно помнить, что сумма в (18.47) является алгебраической.

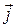
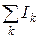
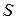
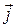
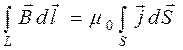
Возможны ситуации, когда токи распределены в пространстве с некоторой плотностью . Этом случае вместо в (18.47) следует взять ток, который протекает через некоторую поверхность , опирающуюся на контур L . При этом поверхность может быть произвольной, единственное требование – она должна опираться на контур L. Суммарный ток через такую поверхность равен потоку вектора через нее. Поэтому соотношение (18.47) можно представить в виде:

(18.48)

По теореме Стокса

. (18.49)

. (18.50)

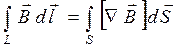
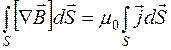
Поверхность интегрирования может быть произвольной (опирающуйся на контур L), поэтому должны быть равны подынтегральные выражения:

. (18.51)

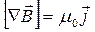
Формулы (18.48) и (18.51) отражают существенное отличие электрического и магнитного полей: циркуляция и ротор вектора напряженности электрического поля равны нулю. Это является следствием того, что электростатическое поле потенциально и может быть описано с помощью скалярного потенциала.

Магнитное поле не является потенциальным, его циркуляция не обязательно равна нулю, его нельзя описать с помощью скалярного потенциала. Такие поля называют вихревыми или соленоидальными.

Дата добавления: 2016-06-02 ; просмотров: 653 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Дивергенция и ротор векторного поля

Электромагнитные поля и волны. Основные понятия и определения

ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

Электрические заряды обусловливают электрические и магнитные явления, например, силовые взаимодействия между заряженными частицами и телами.

Взаимодействие между заряженными частицами или телами осуществляется через электромагнитное поле.

Электромагнитное поле определяется как особый вид материи, характеризующийся способностью распространяться в вакууме со скоростью, близкой к 3×10 8 м/с и оказывающий силовое воздействие на заряженные частицы.

Электромагнитное поле представляет собой единство двух своих составляющих – электрического и магнитного полей.

В каждой точке пространства, где имеет место электромагнитное поле, оно характеризуется величиной и направлением векторов:

Е– напряженности электрического поля;

D – электрического смещения (электрической индукции);

Н – напряженности магнитного поля;

В – магнитной индукции.

Векторы поля D и Н – это функции источников.

Вектор электрического смещения D, Кл/м 2 , равен

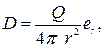
где e_r– орт, направленный вдоль радиус-вектора.

Вектор напряженности магнитного поля Н, А/м , характеризует связь электрического тока с собственным магнитным полем

где — орт в цилиндрической системе координат, у которой ось z совпадает с направлением тока.

Векторы Е и В являются силовыми характеристиками электромагнитного поля.

Эта сила является суперпозицией сил, создаваемых электрической и магнитной составляющими поля:

где – вектор скорости движения заряда.

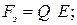Электромагнитные свойства среды

Электромагнитные взаимодействия между зарядами и полями зависят от свойств среды.

Макроскопические параметры среды в каждой точке поля связывают попарно векторы электромагнитного поля:

где J – плотность электрического тока,

s – удельная электрическая проводимость среды.

– абсолютная диэлектрическая проницаемость среды.

– абсолютная магнитная проницаемость.

Данные выражения верны только для изотропных сред.

Классификация сред

Все среды можно классифицировать в зависимости от выбранного признака, положенного в основание классификации. Различают следующие среды:

Дадим каждой среде определение.

Однородная среда — это среда, параметры которой не зависят от координат.

Неоднородная среда — это среда, параметры которой являются функциями координат.

Линейная среда — это среда, параметры которой не зависят от внешнего воздействующего поля, а материальные уравнения носят линейный характер.

Нелинейная среда — это среда, параметры которой зависят от внешнего воздействующего поля.

Изотропная среда — это среда, свойства которой не зависят от направления векторов поля и параметры которой являются скалярными величинами.

Анизотропная среда — это среда, свойства которой зависят от направления векторов поля и параметры среды являются тензорными величинами.

Дивергенция и ротор векторного поля

Дивергенцией или расхождением поля Д называется скаляр, определенный в каждой точке поля и являющийся объемной производной этого поля:

Вычисляется по формуле:

(в декартовых координатах).

Ротор (иначе ротация) поля D есть вектор, определенный в каждой точке поля и являющийся объемной производной этого поля, взятой с обратным знаком:

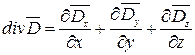
Формула для вычисления в декартовых координатах имеет следующее выражение

Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

Ротор вектор магнитной индукции

Как было показано ранее, одним из важнейших преимуществ многофазных систем является получение вращающегося магнитного поля с помощью неподвижных катушек, на чем основана работа двигателей переменного тока. Рассмотрение этого вопроса начнем с анализа магнитного поля катушки с синусоидальным током.

Магнитное поле катушки с синусоидальным током

При пропускании по обмотке катушки синусоидального тока она создает

магнитное поле, вектор индукции которого изменяется (пульсирует) вдоль этой катушки также по синусоидальному закону Мгновенная ориентация вектора магнитной индукции в пространстве зависит от намотки катушки и мгновенного направления тока в ней и определяется по правилу правого буравчика. Так для случая, показанного на рис. 1, вектор магнитной индукции направлен по оси катушки вверх. Через полпериода, когда при том же модуле ток изменит свой знак на противоположный, вектор магнитной индукции при той же абсолютной величине поменяет свою ориентацию в пространстве на 1800. С учетом вышесказанного магнитное поле катушки с синусоидальным током называют пульсирующим.

Круговое вращающееся магнитное поле
двух- и трехфазной обмоток

Круговым вращающимся магнитным полем называется поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается в пространстве с постоянной угловой частотой.

Для создания кругового вращающегося поля необходимо выполнение двух условий:

Оси катушек должны быть сдвинуты в пространстве друг относительно друга на определенный угол (для двухфазной системы – на 90 0 , для трехфазной – на 120 0 ).
Токи, питающие катушки, должны быть сдвинуты по фазе соответственно пространственному смещению катушек.

Рассмотрим получение кругового вращающегося магнитного поля в случае двухфазной системы Тесла (рис. 2,а).

При пропускании через катушки гармонических токов каждая из них в соответствии с вышесказанным будет создавать пульсирующее магнитное поле. Векторы и , характеризующие эти поля, направлены вдоль осей соответствующих катушек, а их амплитуды изменяются также по гармоническому закону. Если ток в катушке В отстает от тока в катушке А на 90 0 (см. рис. 2,б), то .

Найдем проекции результирующего вектора магнитной индукции на оси x и y декартовой системы координат, связанной с осями катушек:

Модуль результирующего вектора магнитной индукции в соответствии с рис. 2,в равен

(1)

при этом для тангенса угла a , образованного этим вектором с осью абсцисс, можно записать

(2)

Полученные соотношения (1) и (2) показывают, что вектор результирующего магнитного поля неизменен по модулю и вращается в пространстве с постоянной угловой частотой , описывая окружность, что соответствует круговому вращающемуся полю.

Покажем, что симметричная трехфазная система катушек (см. рис. 3,а) также позволяет получить круговое вращающееся магнитное поле.

Каждая из катушек А, В и С при пропускании по ним гармонических токов создает пульсирующее магнитное поле. Векторная диаграмма в пространстве для этих полей представлена на рис. 3,б. Для проекций результирующего вектора магнитной индукции на

оси декартовой системы координат, ось y у которой совмещена с магнитной осью фазы А, можно записать

;

(3)

(4)

Приведенные соотношения учитывают пространственное расположение катушек, но они также питаются трехфазной системой токов с временным сдвигом по фазе на 1200. Поэтому для мгновенных значений индукций катушек имеют место соотношения

; ; .

Подставив эти выражения в (3) и (4), получим:

;

(5)

(6)

В соответствии с (5) и (6) и рис. 2,в для модуля вектора магнитной индукции результирующего поля трех катушек с током можно записать:

а сам вектор составляет с осью х угол a , для которого

Таким образом, и в данном случае имеет место неизменный по модулю вектор магнитной индукции, вращающийся в пространстве с постоянной угловой частотой , что соответствует круговому полю.

Магнитное поле в электрической машине

С целью усиления и концентрации магнитного поля в электрической машине для него создается магнитная цепь. Электрическая машина состоит из двух основных частей (см. рис. 4): неподвижного статора и вращающегося ротора, выполненных соответственно в виде полого и сплошного цилиндров.

На статоре расположены три одинаковые обмотки, магнитные оси которых сдвинуты по расточке магнитопровода на 2/3 полюсного деления , величина которого определяется выражением

где — радиус расточки магнитопровода, а р – число пар полюсов (число эквивалентных вращающихся постоянных магнитов, создающих магнитное поле, — в представленном на рис. 4 случае р=1).

На рис. 4 сплошными линиями (А, В и С) отмечены положительные направления пульсирующих магнитных полей вдоль осей обмоток А, В и С.

Приняв магнитную проницаемость стали бесконечно большой, построим кривую распределения магнитной индукции в воздушном зазоре машины, создаваемой обмоткой фазы А, для некоторого момента времени t (рис. 5). При построении учтем, что кривая изменяется скачком в местах расположения катушечных сторон, а на участках, лишенных тока, имеют место горизонтальные участки.

Заменим данную кривую синусоидой (следует указать, что у реальных машин за счет соответствующего исполнения фазных обмоток для результирующего поля такая замена связана с весьма малыми погрешностями). Приняв амплитуду этой синусоиды для выбранного момента времени t равной ВА, запишем

(7)

;

(8)

(9)

С учетом гармонически изменяющихся фазных токов для мгновенных значений этих величин при сделанном ранее допущении о линейности зависимости индукции от тока можно записать

Подставив последние соотношения в (7)…(9), получим

;

(10)

;

(11)

(12)

Просуммировав соотношения (10)…(12), с учетом того, что сумма последних членов в их правых частях тождественно равна нулю, получим для результирующего поля вдоль воздушного зазора машины выражение

представляющее собой уравнение бегущей волны.

Магнитная индукция постоянна, если . Таким образом, если мысленно выбрать в воздушном зазоре некоторую точку и перемещать ее вдоль расточки магнитопровода со скоростью

то магнитная индукция для этой точки будет оставаться неизменной. Это означает, что с течением времени кривая распределения магнитной индукции, не меняя своей формы, перемещается вдоль окружности статора. Следовательно, результирующее магнитное поле вращается с постоянной скоростью. Эту скорость принято определять в оборотах в минуту:

Принцип действия асинхронного и синхронного двигателей

Устройство асинхронного двигателя соответствует изображению на рис. 4. Вращающееся магнитное поле, создаваемое расположенными на статоре обмотками с током, взаимодействует с токами ротора, приводя его во вращение. Наибольшее распространение в настоящее время получил асинхронный двигатель с короткозамкнутым ротором ввиду своей простоты и надежности. В пазах ротора такой машины размещены токонесущие медные или алюминиевые стержни. Концы всех стержней с обоих торцов ротора соединены медными или алюминиевыми же кольцами, которые замыкают стержни накоротко. Отсюда и произошло такое название ротора.

В короткозамкнутой обмотке ротора под действием ЭДС, вызываемой вращающимся полем статора, возникают вихревые токи. Взаимодействуя с полем, они вовлекают ротор во вращение со скоростью , принципиально меньшей скорости вращения поля Отсюда название двигателя — асинхронный.

называется относительным скольжением. Для двигателей нормального исполнения S=0,02…0,07. Неравенство скоростей магнитного поля и ротора становится очевидным, если учесть, что при вращающееся магнитное поле не будет пересекать токопроводящих стержней ротора и, следовательно, в них не будут наводиться токи, участвующие в создании вращающегося момента.

Принципиальное отличие синхронного двигателя от асинхронного заключается в исполнении ротора. Последний у синхронного двигателя представляет собой магнит, выполненный (при относительно небольших мощностях) на базе постоянного магнита или на основе электромагнита. Поскольку разноименные полюсы магнитов притягиваются, то вращающееся магнитное поле статора, которое можно интерпретировать как вращающийся магнит, увлекает за собой магнитный ротор, причем их скорости равны. Это объясняет название двигателя – синхронный.

В заключение отметим, что в отличие от асинхронного двигателя, у которого обычно не превышает 0,8…0,85, у синхронного двигателя можно добиться большего значения и сделать даже так, что ток будет опережать напряжение по фазе. В этом случае, подобно конденсаторным батареям, синхронная машина используется для повышения коэффициента мощности.

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.

Какое поле называется пульсирующим?
Какое поле называется вращающимся круговым?
Какие условия необходимы для создания кругового вращающегося магнитного поля?
Какой принцип действия у асинхронного двигателя с короткозамкнутым ротором?
Какой принцип действия у синхронного двигателя?
На какие синхронные скорости выпускаются в нашей стране двигатели переменного тока общепромышленного исполнения?