Предложенные диктанты адресованы учителям, работающим по учебнику «Геометрия. 8 класс» (авторы А.Г. Мерзляк В.Б. Полонский, М.С. Якир), но могут быть использованы и учителями, работающими по другим учебникам.
- Просмотр содержимого документа «Математические диктанты по геометрии, 8 класс»
- Геометрический диктант по теме «Четырёхугольники» (8класс)
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
- ЧЕТЫРЕХУГОЛЬНИКИ — Урок 2 — МАТЕМАТИЧЕСКИЕ ДИКТАНТЫ
- 🌟 Видео
Просмотр содержимого документа
«Математические диктанты по геометрии, 8 класс»
Математические диктанты по геометрии
(8 класс, учебник авт. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир)
Диктант 1 по теме «Четырёхугольник и его элементы»
Запишите окончание предложения.
1) Два отрезка называют соседними, если . .
2) Соседними сторонами четырёхугольника называют . .
3) Соседними вершинами четырёхугольника называют . .
4) Противолежащими сторонами четырёхугольника называют . .
5) Противолежащими вершинами четырёхугольника называют . .
6) Периметром четырёхугольника называют . .
7) Диагональю четырёхугольника называют . .
8) Четырёхугольник называют выпуклым, если . .
Сформулируйте теорему о сумме углов четырёхугольника.
Запишите стороны четырёхугольника DEFK, являющиеся соседними со стороной EF.
Запишите сторону четырёхугольника MPON, являющуюся противолежащей стороне MP.
Запишите вершины четырёхугольника BCKD, являющиеся соседними с вершиной D.
Запишите вершину четырёхугольника BCKD, являющуюся противолежащей вершине P.
Начертите четырёхугольник, обозначьте его вершины последовательно буквами A, M, K и F. Запишите какие-либо три обозначения этого четырёхугольника.
Начертите четырёхугольник, у которого один угол тупой, один угол — прямой, а два других — острые.
Начертите четырёхугольник, у которого диагонали перпендикулярны и точкой пересечения делятся пополам.
Чему равен четвёртый угол четырёхугольника, если три его угла равны 50°, 70° и 130°?
Чему равны стороны четырёхугольника, если каждая из них меньше его периметра на 12 см?
Диктант 2 по теме «Параллелограмм. Свойства параллелограмма»
Запишите окончание предложения.
1) Параллелограммом называют . .
2) Высотой параллелограмма называют . .
Сформулируйте свойство противолежащих сторон параллелограмма.
Сформулируйте свойство противолежащих углов параллелограмма.
Сформулируйте свойство диагоналей параллелограмма.
Начертите произвольный треугольник и проведите через каждую его вершину прямую, параллельную противолежащей стороне. Сколько параллелограммов образовалось на рисунке?
Проведите три параллельные прямые и ещё две параллельные прямые, которые пересекаются с первыми тремя прямыми. Сколько параллелограммов образовалось на рисунке?
Найдите периметр параллелограмма, стороны которого равны 16 см и 14 см.
Периметр параллелограмма равен 70 см, а сумма двух его сторон — 50 см. Найдите меньшую сторону параллелограмма.
Сумма трёх сторон параллелограмма равна 40 см. Найдите стороны параллелограмма, если его периметр равен 52 см.
Один из углов параллелограмма равен 20°. Запишите градусные меры трёх остальных его углов.
Сумма двух углов параллелограмма равна 150°. Найдите больший угол параллелограмма.
Найдите углы параллелограмма, если сумма трёх его углов равна 280°.
Верно ли, что любой параллелограмм имеет два угла, сумма которых равна 180°? Ответ обоснуйте.
Верно ли, что любой параллелограмм имеет два острых и два тупых угла? Ответ обоснуйте.
В параллелограмме ABCD ∠B + ∠D
Диагонали параллелограмма ABCD пересекаются в точке O.
1) Какой отрезок является медианой треугольника ABD?
2) Медианой какого треугольника является отрезок DO?
Точка пересечения диагоналей параллелограмма удалена от одной из его вершин на 7 см, а от другой — на 10 см. Какова длина диагоналей параллелограмма?
Диктант 3 по теме «Прямоугольник»
Запишите окончание предложения.
1) Прямоугольником называют . .
2) Параллелограмм является прямоугольником, если один из его углов . .
3) Параллелограмм является прямоугольником, если его диагонали . .
Запишите свойства, которыми обладает прямоугольник как любой параллелограмм.
Запишите свойства прямоугольника, которыми не обладает параллелограмм, отличный от прямоугольника.
Является ли прямоугольником параллелограмм, имеющий прямой угол?
Всякий ли четырёхугольник, имеющий прямой угол, является прямоугольником?
Сделайте рисунок, опровергающий утверждение.
1) Четырёхугольник, имеющий два прямых угла, является прямоугольником.
2) Четырёхугольник, диагонали которого равны, является прямоугольником.
В прямоугольнике ABCD AB = 4 см, AD = 9 см. Чему равно расстояние:
1) от вершины C до прямой AD;
2) от вершины B до прямой CD?
Сумма длин диагоналей прямоугольника равна 15 см. Чему равна длина его диагонали?
Диагональ прямоугольника образует с одной из его сторон угол 24°. Какой угол образует эта диагональ с другой стороной прямоугольника?
Угол между диагоналями прямоугольника равен 40°. Какие углы образует диагональ прямоугольника с его сторонами?
Периметр прямоугольника равен 24 см, а одна из его сторон — 4 см. Найдите сторону прямоугольника, соседнюю с данной его стороной.
Диагонали прямоугольника ABCD пересекаются в точке O, OC = 8 см. Какова длина диагонали BD?
Диктант 4 по теме «Ромб»
Запишите окончание предложения.
1) Ромбом называют . .
2) Параллелограмм является ромбом, если его диагонали . .
3) Параллелограмм является ромбом, если его диагональ . .
Запишите свойства, которыми обладает ромб как любой параллелограмм.
Запишите свойства, которыми не обладает параллелограмм, отличный от ромба.
Диагонали ромба ABCD пересекаются в точке O. Укажите:
1) биссектрису треугольника BCD;
2) медиану треугольника ABC;
3) высоту треугольника ADC.
Угол между диагональю ромба и его стороной равен 24°. Чему равен угол между другой диагональю ромба и той же стороной?
Найдите сторону ромба, если его периметр на 27 см больше этой стороны.
Может ли прямоугольник быть ромбом? Если да, то укажите, в каком случае это возможно.
Может ли диагональ ромба быть перпендикулярной его стороне? Ответ обоснуйте.
Может ли диагональ ромба быть равной его стороне? Ответ обоснуйте.
Периметр ромба ABCD равен 36 см, а его диагональ BD равна 9 см. Какова градусная мера угла C?
Сделайте рисунок, опровергающий утверждение:
1) четырёхугольник, диагонали которого перпендикулярны, является ромбом;
2) четырёхугольник, диагональ которого делит его угол пополам, является ромбом.
Диктант 5 по теме «Квадрат»
Запишите свойства квадрата, которыми не обладает прямоугольник, отличный от квадрата.
Запишите свойства квадрата, которыми не обладает ромб, отличный от квадрата.
Сделайте рисунок, опровергающий утверждение: четырёхугольник, диагонали которого равны и перпендикулярны, является квадратом.
Найдите периметр квадрата, если он на 18 см больше его стороны.
Диагонали квадрата ABCD пересекаются в точке O, BD = 24 см. Чему равна длина отрезка CO?
Как, используя только циркуль, проверить, является ли четырёхугольник квадратом?
Диктант 6 по теме «Средняя линия треугольника»
Запишите окончание предложения.
1) Средней линией треугольника называют . .
2) Средняя линия треугольника, соединяющая середины двух его сторон, параллельна . .
3) Средняя линия треугольника, соединяющая середины двух его сторон, равна . .
Сторона треугольника равна 7 см. Чему равна средняя линия треугольника, параллельная этой стороне?
Точки M, K и N — середины сторон треугольника ABC. Периметр треугольника MKN равен 16 см. Чему равен периметр треугольника ABC?
Чему равен периметр равностороннего треугольника, средняя линия которого равна 6 см?
Существует ли треугольник, в котором две средние линии равны? В случае утвердительного ответа укажите вид этого треугольника.
Существует ли треугольник, в котором все средние линии равны? В случае утвердительного ответа укажите вид этого треугольника.
Сделайте рисунок, опровергающий утверждение: если концы отрезка лежат на двух сторонах треугольника, а длина этого отрезка равна половине третьей стороны, то этот отрезок — средняя линия треугольника.
Диагональ квадрата равна 9 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного квадрата.
Диктант 7 по теме «Трапеция»
Запишите окончание предложения.
1) Трапецией называют четырёхугольник, у которого . .
2) Основаниями трапеции называют . .
3) Боковыми сторонами трапеции называют . .
4) Высотой трапеции называют . .
5) Равнобокой называют трапецию, у которой . .
6) Прямоугольной называют трапецию, у которой . .
7) Средней линией трапеции называют . .
8) Средняя линия трапеции параллельна . .
9) Средняя линия трапеции равна . .
10) Углы при каждом основании равнобокой трапеции . .
11) Диагонали равнобокой трапеции . .
Можно ли утверждать, что четырёхугольник, у которого есть две параллельные стороны, является трапецией? Ответ обоснуйте.
Могут ли быть равными соседние углы трапеции? Ответ обоснуйте.
Могут ли быть равными противолежащие углы трапеции? Ответ обоснуйте.
Существует ли трапеция, у которой:
1) один прямой угол;
2) два прямых угла;
3) один острый угол;
4) два острых угла;
5) один тупой угол;
6) два тупых угла;
7) три тупых угла?
Может ли один из углов при большем основании трапеции быть острым, а другой — тупым? В случае утвердительного ответа изобразите такую трапецию.
Два угла трапеции равны 70° и 150°. Чему равны два других угла трапеции?
Сумма трёх углов равнобокой трапеции равна 220°. Найдите углы трапеции.
Две противолежащие стороны равнобокой трапеции равны 3 см и 7 см, а третья сторона равна 4 см. Чему равен периметр трапеции?
Найдите периметр равнобокой трапеции, боковая сторона которой равна 8 см, а средняя линия — 12 см.
Периметр равнобокой трапеции равен 26 см, а боковая сторона — 6 см. Чему равна средняя линия трапеции?
Диктант 8 по теме «Центральные и вписанные углы»
Запишите окончание предложения.
1) Центральным углом окружности называют . .
2) Градусную меру дуги считают равной градусной мере . .
3) Вписанным углом окружности называют . .
4) Градусная мера вписанного угла равна . .
5) Вписанные углы, опирающиеся на одну и ту же дугу, . .
6) Вписанный угол, опирающийся на диаметр (полуокружность), является . .
Сделайте рисунок, опровергающий утверждение:
1) если вершина угла лежит на окружности, то этот угол является вписанным углом окружности;
2) если стороны угла пересекают окружность, то этот угол является вписанным углом окружности.
3. Начертите окружность произвольного радиуса и какой-либо её вписанный угол DEF. Постройте ещё два вписанных угла, равных углу DEF.
4. Могут ли не быть равными вписанные в одну окружность углы ABC и ADC? В случае утвердительного ответа проиллюстрируйте его рисунком.
5. Могут ли быть равными два вписанных в одну окружность угла, если они не опираются на одну дугу? В случае утвердительного ответа проиллюстрируйте его рисунком.
6. Каким углом, острым, прямым или тупым, является вписанный угол, если дуга, на которую он опирается:
1) больше полуокружности;
2) меньше полуокружности;
3) равна полуокружности?
7. Определите вид вписанного угла, если одна из его сторон проходит через центр окружности.
8. Чему равна градусная мера центрального угла окружности, опирающегося на дугу, которая составляет:
1) 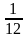
2) 
3) 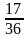
4) 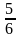
9. Чему равна градусная мера вписанного угла окружности, опирающегося на дугу, которая составляет:
1) 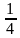
2) 
3) 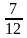
4) 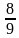
10. Какова градусная мера центрального угла окружности, если он на 40° больше вписанного угла, опирающегося на ту же дугу, что и центральный угол?
Диктант 9 по теме «Описанная и вписанная окружности четырёхугольника»
Запишите окончание предложения.
1) Окружность называют описанной около четырёхугольника, если . .
2) Если четырёхугольник является вписанным в окружность, то сумма его противолежащих углов . .
3) Около четырёхугольника можно описать окружность, если . .
4) Центр описанной окружности четырёхугольника равноудалён от . .
5) Чтобы найти центр описанной окружности четырёхугольника, достаточно найти точку пересечения . .
6) Окружность называют вписанной в четырёхугольник, если . .
7) Если четырёхугольник является описанным около окружности, то сумма его противолежащих сторон . .
8) В выпуклый четырёхугольник можно вписать окружность, если . .
9) Центр вписанной окружности четырёхугольника равноудалён от . .
10) Чтобы найти центр вписанной окружности четырёхугольника, достаточно найти точку пересечения . .
В какой прямоугольник можно вписать окружность?
Можно ли описать окружность около четырёхугольника, у которого только один прямой угол? Ответ обоснуйте.
Можно ли описать окружность около четырёхугольника, у которого только два прямых угла? Ответ обоснуйте.
Можно ли описать окружность около прямоугольной трапеции? Ответ обоснуйте.
Найдите неизвестные углы вписанного четырёхугольника, если два его угла равны 36° и 145°.
Найдите неизвестные углы вписанной трапеции, если один из её углов равен 75°.
Во вписанном в окружность четырёхугольнике ABCD угол C является наименьшим. Какой угол является наибольшим углом этого четырёхугольника?
Около какого ромба можно описать окружность?
Можно ли вписать окружность в трапецию, три стороны которой равны? Ответ обоснуйте.
Найдите периметр четырёхугольника, описанного около окружности, три последовательные стороны которого равны 8 см, 10 см и 13 см.
Три последовательные стороны четырёхугольника, в который вписана окружность, равны 5 см, 6 см и 8 см. Чему равна четвёртая сторона четырёхугольника?
Боковые стороны трапеции, описанной около окружности, равны 12 см и 26 см. Найдите среднюю линию трапеции.
Периметр равнобокой трапеции, описанной около окружности, равен 48 см. Чему равна средняя линия трапеции?
В описанном около окружности четырёхугольнике ABCD сторона BC является наибольшей. Какая сторона является наименьшей стороной этого четырёхугольника?
Радиус окружности, вписанной в трапецию, равен 14 см. Чему равно расстояние между прямыми, на которых лежат основания трапеции?
Диктант 10 по теме «Теорема Фалеса. Теорема о пропорциональных отрезках»
Запишите окончание предложения.
1) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то . .
2) Отношением двух отрезков называют . .
3) Если параллельные прямые пересекают стороны угла, то отрезки, образовавшиеся на одной стороне угла, пропорциональны . .
4) Три медианы треугольника пересекаются в одной точке, которая делит каждую из них . .
5) Биссектриса треугольника делит его сторону на отрезки . .
Три параллельные прямые пересекают стороны угла так, что на одной из его сторон образовались три равных отрезка, а один из отрезков, образовавшийся на второй стороне, равен 12 см. Чему равна сумма длин всех трёх отрезков, образовавшихся на второй стороне?
Три параллельные прямые пересекают стороны угла так, что на одной из его сторон образовались два отрезка длиной 16 см и 28 см, а один из отрезков, образовавшихся на второй стороне, равен 56 см. Найдите неизвестный отрезок, образовавшийся на второй стороне угла. Сколько решений имеет задача?
Точка пересечения медиан треугольника делит одну из медиан на отрезки, один из которых на 6 см больше другого. Какова длина этой медианы?
В каком отношении высоты равностороннего треугольника делятся точкой их пересечения?
Через точку пересечения медиан треугольника проведена прямая, параллельная одной из сторон треугольника. В каком отношении эта прямая делит каждую из двух других сторон треугольника?
Биссектриса равностороннего треугольника равна 12 см. Чему равен радиус окружности, описанной около этого треугольника?
Отрезок AD — биссектриса треугольника ABC, AB AC. Сравните отрезки BD и CD.
Две стороны треугольника равны 20 см и 45 см, а биссектриса угла между ними делит третью сторону на отрезки, меньший из которых равен 16 см. Найдите неизвестную сторону треугольника.
Диктант 11 по теме «Подобные треугольники»
Запишите окончание предложения.
1) Два треугольника называют подобными, если . .
2) Коэффициентом подобия двух подобных треугольников называют число, которое равно . .
3) Любые два равных треугольника подобны с коэффициентом подобия, равным . .
4) Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от . .
Запишите, используя соответствующую символику, что треугольник DEF подобен треугольнику MNK с коэффициентом подобия, равным 4,5.
Начертите какие-нибудь два подобных, но неравных треугольника.
Треугольник ABC подобен треугольнику A1B1C1 с коэффициентом подобия, равным 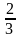
B1C1 = 9 см.
Могут ли быть подобными остроугольный и прямоугольный треугольники? Ответ обоснуйте.
Могут ли быть подобными разносторонний и равнобедренный треугольники? Ответ обоснуйте.
Подобны ли два треугольника, если стороны одного равны 2 см, 3 см и 4 см, а другого — 14 см, 21 см и 32 см? Ответ обоснуйте.
Треугольник ABC подобен треугольнику DEF с коэффициентом подобия, равным 
Треугольник ABC подобен треугольнику A1B1C1 с коэффициентом подобия, равным 1,5. Стороны треугольника A1B1C1 равны 25 см, 20 см и 15 см. Найдите периметр треугольника ABC.
Точки M и K — середины сторон AB и BC треугольника ABC соответственно. Подобны ли треугольники ABC и MBK? Ответ обоснуйте. В случае утвердительного ответа укажите коэффициент подобия.
В треугольнике проведены все средние линии. Сколько образовалось треугольников, подобных данному?
Диктант 12 по теме «Первый признак подобия треугольников»
Сформулируйте первый признак подобия треугольников.
Даны треугольники ABC и DEF. Известно, что ∠A = ∠D, ∠B = ∠E, AB : DE = 3 : 2,
AC = 18 см. Чему равна сторона DF?
Могут ли быть подобными треугольник с углом 20° и треугольник с углом 110°? Ответ обоснуйте.
Могут ли быть подобными треугольник с углом 40° и треугольник с углом 140°? Ответ обоснуйте.
Подобны ли два прямоугольных треугольника, если один из них имеет угол 25°, а другой — 65°? Ответ обоснуйте.
Могут ли быть подобными два треугольника, один из которых равнобедренный, а другой — тупоугольный? Ответ обоснуйте.
Можно ли утверждать, что любые два равнобедренных прямоугольных треугольника подобны? Ответ обоснуйте.
Диктант 13 по теме «Метрические соотношения в прямоугольном треугольнике»
Запишите окончание предложения.
1) Высота прямоугольного треугольника, проведённая к гипотенузе, делит треугольник на . .
2) Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению . .
3) Квадрат катета равен произведению . .
Начертите прямоугольный треугольник, обозначьте его вершины буквами M, K и D, где D — вершина прямого угла. Проведите высоту DA треугольника.
1) Запишите отрезок, являющийся проекцией катета DM на гипотенузу.
2) Запишите отрезок, являющийся проекцией катета DK на гипотенузу.
Проекции катетов прямоугольного треугольника на гипотенузу равны 18 см и 32 см. Найдите меньший катет данного треугольника.
Чему равна высота прямоугольного треугольника, проведённая к гипотенузе, если проекции катетов на гипотенузу равны 2 см и 72 см?
Чему равна гипотенуза прямоугольного треугольника, если один из его катетов равен 6 см, а проекция этого катета на гипотенузу равна 4 см?
Чему равна проекция катета прямоугольного треугольника на гипотенузу, если этот катет равен 9 см, а гипотенуза — 27 см?
Диктант 14 по теме «Тригонометрические функции острого угла прямоугольного треугольника»
Запишите окончание предложения.
1) Синусом острого угла прямоугольного треугольника называют . .
2) Косинусом острого угла прямоугольного треугольника называют . .
3) Тангенсом острого угла прямоугольного треугольника называют . .
4) Котангенсом острого угла прямоугольного треугольника называют . .
5) Синус, косинус, тангенс и котангенс острого угла зависят только от . .
6) Синус и косинус острого угла меньше . .
Запишите тождество, связывающее тангенс, синус и косинус одного и того же угла.
Запишите тождество, связывающее котангенс, синус и косинус одного и того же угла.
Запишите тождество, связывающее тангенс и котангенс одного и того же угла.
Запишите основное тригонометрическое тождество.
Запишите, чему равен:
1) sin (90° − α); 2) cos (90° − α);
3) tg (90° − α); 4) ctg (90° − α).
Запишите, какому числу равен:
1) sin 45°; 2) cos 45°; 3) tg 45°; 4) ctg 45°.
Запишите, какому числу равен:
1) sin 30°; 2) cos 30°; 3) tg 30°; 4) ctg 30°.
Запишите, какому числу равен:
1) sin 60°; 2) cos 60°; 3) tg 60°; 4) ctg 60°.
Известно, что tgα = 
Известно, что cosα = 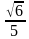
Найдите значение выражения:
1) sin 2 26° + sin 2 64°; 2) tg 2 70°ctg 2 20°.
Стороны прямоугольного треугольника равны 6 см, 8 см и 10 см. Найдите:
1) синус меньшего острого угла треугольника;
2) косинус большего острого угла треугольника;
3) тангенс меньшего острого угла треугольника;
4) котангенс меньшего острого угла треугольника.
Существует ли такой угол α, что:
1) sinα = 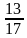
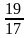
3) tg α= 0,35; 4) ctg α=2000?
В треугольнике DEF с прямым углом D DE DF. Какой из острых углов треугольника имеет:
1) больший синус; 2) больший котангенс?
В треугольнике ABC с прямым углом C sin A = 0,2. Чему равен cos B?
В треугольнике ABC с прямым углом C tg A = 4. Чему равно произведение tg Actg B?
Может ли синус острого угла прямоугольного треугольника быть равным его тангенсу? Ответ обоснуйте.
Синус острого угла вдвое больше его косинуса. Чему равен тангенс данного угла?
Диктант 15 по теме «Решение прямоугольных треугольников»
Запишите окончание предложения.
1) Катет прямоугольного треугольника равен произведению гипотенузы на синус угла, . .
2) Катет прямоугольного треугольника равен произведению гипотенузы на косинус угла, . .
3) Катет прямоугольного треугольника равен произведению другого катета на тангенс угла, . .
4) Катет прямоугольного треугольника равен произведению другого катета на котангенс угла, . .
5) Гипотенуза прямоугольного треугольника равна частному от делению катета на синус . .
6) Гипотенуза прямоугольного треугольника равна частному от делению катета на косинус . .
Можно ли решить прямоугольный треугольник:
1) по двум сторонам;
2) по двум острым углам;
3) по стороне и острому углу?
Чему равен катет прямоугольного треугольника, гипотенуза которого равна 10 см, а прилежащий к искомому катету острый угол — 45°?
Чему равен катет прямоугольного треугольника, второй катет которого равен 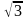
Чему равна гипотенуза прямоугольного треугольника, катет которого равен 2 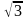
В треугольнике ABC с прямым углом C AC = 12 см, ctg B = 6. Чему равен катет BC?
В треугольнике DEF с прямым углом D EF = 8 см, sin F = 0,4. Чему равен катет DE?
В треугольнике DEF с прямым углом D DE = 8 см, sin F = 0,4. Чему равна гипотенуза EF?
Высота равнобедренного треугольника, проведённая к основанию, равна h, угол при основании треугольника равен β. Чему равно основание треугольника?
Боковая сторона равнобедренного треугольника равна a, угол при вершине треугольника равен α. Чему равна высота треугольника, проведённая к основанию?
Диктант 16 по теме «Многоугольники»
Запишите окончание предложения.
1) Периметром многоугольника называют . .
2) Диагональю многоугольника называют отрезок, соединяющий . .
3) Выпуклым называют многоугольник, все углы которого . .
4) Выпуклый многоугольник расположен в одной полуплоскости относительно . .
5) Сумма углов выпуклого n-угольника равна . .
6) Окружность называют описанной около многоугольника, если . .
7) Около многоугольника можно описать окружность, если существует точка, равноудалённая от . .
8) Если серединные перпендикуляры всех сторон многоугольника пересекаются в одной точке, то . .
9) Окружность называют вписанной в многоугольник, если . .
10) В выпуклый многоугольник можно вписать окружность, если существует точка, равноудалённая от . .
11) Если биссектрисы всех углов выпуклого многоугольника пересекаются в одной точке, то . .
Начертите произвольный выпуклый пятиугольник.
Начертите произвольный пятиугольник, не являющийся выпуклым.
Начертите восьмиугольник, каждый угол которого равен 135°, а каждая сторона —
3 см. Опишите около этого восьмиугольника окружность и впишите в него окружность.
Чему равна сумма углов выпуклого 102-угольника?
Сколько сторон имеет выпуклый многоугольник, сумма углов которого равна 1260°?
Диагональ разбивает выпуклый шестиугольник на два многоугольника, один из которых является четырёхугольником. Определите вид другого многоугольника.
Диагональ разбивает выпуклый n-угольник на два многоугольника, один из которых является треугольником. Определите вид другого многоугольника.
Периметр семиугольника, все стороны которого равны, на 42 см больше его стороны. Чему равна сторона семиугольника?
При каком значении n любой n-угольник является выпуклым?
Диктант 17 по теме «Понятие площади многоугольника. Площадь прямоугольника»
Запишите окончание предложения.
1) Площадью многоугольника называют положительную величину, которая обладает следующими свойствами . .
2) Измерить площадь многоугольника — это значит . .
3) Числовое значение площади называют . .
4) Площадь прямоугольника равна . .
5) Равновеликими называют многоугольники, имеющие . .
Многоугольник разделён на три многоугольника, площади которых равны 10 см 2 ,
20 см 2 и 30 см 2 . Чему равна площадь данного многоугольника?
Найдите площадь прямоугольника, стороны которого равны 0,8 м и 30 см.
Найдите неизвестную сторону прямоугольника, если его площадь и одна из сторон соответственно равны 270 см 2 и 3 дм.
Стороны прямоугольника равны 4 см и 9 см. Чему равна сторона равновеликого ему квадрата?
Сделайте рисунок, опровергающий утверждение: если два прямоугольника имеют равные периметры, то они являются равновеликими.
Верно ли утверждение?
1) Два равновеликих прямоугольника равны.
2) Два равновеликих квадрата равны.
Сторона квадрата равна большей стороне прямоугольника. Какой из этих четырёхугольников имеет бóльшую площадь?
Как изменится площадь квадрата, если его сторону:
2) уменьшить вдвое?
Во сколько раз надо уменьшить сторону квадрата, чтобы его площадь уменьшилась в 36 раз?
Как изменится площадь прямоугольника, если:
1) каждую его сторону увеличить в 4 раза;
2) две его противолежащие стороны уменьшить в 5 раз;
3) две его противолежащие стороны увеличить в 6 раз, а две другие — уменьшить в 3 раза?
Диктант 18 по теме «Площадь параллелограмма»
Запишите окончание предложения.
Площадь параллелограмма равна произведению . .
Запишите формулу, по которой вычисляют площадь S параллелограмма, сторона которого равна a, а проведённая к ней высота — h.
Чему равна площадь параллелограмма, сторона которого равна 12 см, а проведённая к ней высота — 50 мм?
Площадь параллелограмма равна 40 см 2 , а его стороны — 8 см и 10 см. Чему равна бóльшая высота параллелограмма?
Площадь параллелограмма равна 48 см 2 , а его высоты — 4 см и 6 см. Чему равна меньшая сторона параллелограмма?
Диктант 19 по теме «Площадь треугольника»
Запишите окончание предложения.
1) Площадь треугольника равна . .
2) Площадь прямоугольного треугольника равна . .
Запишите формулу, по которой вычисляют площадь S треугольника, сторона которого равна a, а проведённая к ней высота — h.
Запишите формулу, по которой можно вычислить площадь S прямоугольного треугольника, катеты которого равны a и b.
Запишите формулу, по которой можно вычислить площадь S ромба, диагонали которого равны d1 и d2.
Чему равна площадь треугольника, сторона которого равна 18 см, а проведённая к ней высота — 6 см?
Чему равна сторона треугольника, площадь которого равна 20 см 2 , а проведённая к искомой стороне высота — 8 см?
Чему равна высота треугольника, площадь которого равна 24 см 2 , а сторона, к которой проведена искомая высота, — 4 см?
Найдите площадь прямоугольного треугольника, катеты которого равны 20 см и 30 см.
Чему равна площадь ромба, диагонали которого равны 6 см и 14 см?
Сторона и проведённая к ней высота треугольника равны соответственно стороне и проведённой к ней высоте параллелограмма. Чему равно отношение площади данного треугольника к площади параллелограмма?
Площадь треугольника ABC равна 64 см 2 , отрезок BM — медиана этого треугольника. Чему равна площадь треугольника ABM?
Может ли биссектриса треугольника делить его на два равновеликих треугольника? Ответ обоснуйте.
Может ли высота треугольника делить его на два равновеликих треугольника? Ответ обоснуйте.
Что такое геометрическое место точек, являющихся вершинами равновеликих треугольников, имеющих общую сторону AB?
Диктант 20 по теме «Площадь трапеции»
Запишите окончание предложения.
Площадь трапеции равна произведению . .
Запишите формулу, по которой вычисляют площадь S трапеции, основания которой равны a и b, а высота — h.
Чему равна площадь трапеции, основания которой равны 7 см и 8 см, а высота — 6 см?
Найдите высоту трапеции, основания которой равны 6 см и 14 см, а площадь — 90 см 2 .
Найдите среднюю линию трапеции, площадь которой равна 40 см 2 , а высота — 8 см.
Высота равнобокой трапеции, равная 10 см и проведённая из вершины тупого угла трапеции, делит её основание на отрезки, больший из которых равен 21 см. Чему равна площадь трапеции?
Боковые стороны прямоугольной трапеции, в которую можно вписать окружность, равны 8 см и 12 см. Чему равна площадь трапеции?
Боковая сторона равнобокой трапеции, в которую можно вписать окружность, равна
9 см, а площадь трапеции — 72 см 2 . Найдите радиус окружности, вписанной в трапецию.
Диагональ равнобокой трапеции равна 6 см. Чему равна площадь трапеции, если её диагонали перпендикулярны?
Видео:ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

Геометрический диктант по теме «Четырёхугольники» (8класс)
Видео:МЕРЗЛЯК-8. ГЕОМЕТРИЯ. ЧЕТЫРЕХУГОЛЬНИК. ПАРАГРАФ-1. ТЕОРИЯСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Выбранный для просмотра документ Буквенный диктант по геометрии для 8 класса.doc
Методика проведения буквенного диктанта по геометрии в 8 классе.
Данный вид диктанта проводится по окончании изучения главы на повторительно-обобщающем уроке, когда необходимо проверить и оценить знания, умения и навыки учащихся по изученным темам.
Каждое определение, признак или теорема зашифровано буквой алфавита (например, А – четырёхугольник, Р — теорема Фалеса, И – признак параллелограмма) и записаны на доске (или представлены на слайде).
Учитель диктует учащимся вопросы поочерёдно по вариантам (определение, теорему или признак), учащиеся ищут ответ среди зашифрованных ответов.
Задания составляются в двух вариантах:
Нечётные номера вопросов для первого варианта, чётные — для второго. Учащиеся записывают в качестве ответа только букву.
Фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.
Отрезки, соединяющие вершины.
Вершины, являющиеся концами одной из сторон четырёхугольника.
Вершины, не являющиеся соседними.
Отрезки, соединяющие противолежащие вершины четырёхугольника.
Стороны, исходящие из одной вершины.
Стороны, не имеющие общего конца.
Четырёхугольник, у которого противолежащие стороны параллельны.
Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
У параллелограмма противолежащие стороны равны.
Параллелограмм, у которого все углы прямые.
У параллелограмма противолежащие углы равны.
Параллелограмм, у которого все стороны равны.
Параллелограмм, у которого все стороны равны.
Если параллельные прямые, пересекающие стороны угла, отсекают на одной из сторон равные
отрезки, то они отсекают равные отрезки и на другой его стороне.
Отрезок, соединяющий середины двух сторон треугольника.
Четырёхугольник, у которого только две противолежащие стороны параллельны.
Трапеция, у которой боковые стороны равны.
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные
Свойство диагоналей параллелограмма
Свойство противолежащих сторон параллелограмма
Свойство противолежащих углов параллелограмма
Средняя линия треугольника
Обобщённая теорема Фалеса
Такая методика проверки знаний, умений и навыков учащихся позволяет:
— учитывать индивидуальные особенности учащихся;
-проверить качество усвоения теоретического материала;
— сэкономить время на опрос учащихся;
— оперативно проверить и оценить выполнение работы.
Выбранный для просмотра документ Презентация Буквенный геометрический диктант в 8 классе.ppt
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Урок геометрии в 8классе Буквенный геометрический диктант по теме «Четырёхугольники»
№ Формулировка вопроса 1. Фигура, которая состоит из 4 точек и 4 последовательно соединяющих их отрезков. 2. Отрезки, соединяющие вершины. 3. Вершины, являющиеся концами одной из сторон четырёхугольника. 4. Вершины, не являющиеся соседними. 5. Отрезки, соединяющие противолежащие вершины четырёхугольника. 6. Стороны, исходящие из одной вершины. 7. Стороны, не имеющие общего конца. 8. Четырёхугольник, у которого противолежащие стороны параллельны.
9. Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот 4-угольник-параллелограмм. 10 Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. 11 У параллелограмма противолежащие стороны равны. 12 Параллелограмм, у которого все углы прямые. 13 У параллелограмма противолежащие углы равны. 14 Параллелограмм, у которого все стороны равны. 15 Параллелограмм, у которого все стороны равны.
16 Если параллельные прямые, пересекающие стороны угла, отсекают на одной из сторон равные отрезки, то они отсекают равные отрезки и на другой его стороне. 17 Отрезок, соединяющий середины двух сторон треугольника. 18 Четырёхугольник, у которого только две противолежащие стороны параллельны. 19 Трапеция, у которой боковые стороны равны. 20 Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
Учащиеся записывают ответ буквой А Четырёхугольник Б Стороны В Соседние вершины Г Противолежащие вершины Д Диагонали Е Соседние стороны Ж Противолежащие стороны
З Параллелограмм И Признак параллелограмма К Свойство диагоналей параллелограмма Л Свойство противолежащих сторон параллелограмма М Прямоугольник Н Свойство противолежащих углов параллелограмма О Ромб
П Квадрат Р Теорема Фалеса С Средняя линия треугольника Т Трапеция У Равнобокая трапеция Ф Обобщённая теорема Фалеса
ОТВЕТЫ К ДИКТАНТУ Вариант 1 Вариант 2 1. А 2. Б 3. В 4. Г 5. Д 6. Е 7. Ж 8. З 9. И 10. К 11. Л 12. М 13. Н 14. О 15. П 16. Р 17. С 18. Т 19. У 20. Ф
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 967 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 341 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
- Еременко Наталья АлександровнаНаписать 3936 11.11.2015
Номер материала: ДВ-147484
- 11.11.2015 457
- 11.11.2015 479
- 11.11.2015 5409
- 11.11.2015 714
- 11.11.2015 825
- 11.11.2015 908
- 11.11.2015 630
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Россия направит $10,3 млн на развитие школьного питания в нескольких странах
Время чтения: 1 минута
Названы главные риски для детей на зимних каникулах
Время чтения: 3 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

ЧЕТЫРЕХУГОЛЬНИКИ — Урок 2 — МАТЕМАТИЧЕСКИЕ ДИКТАНТЫ
МАТЕМАТИЧЕСКИЙ ДИКТАНТ № 1. Определение параллелограмма
1. Начертите параллелограмм ABCD. Проведите в нем диагонали АС и BD. Обозначьте их точку пересечения буквой О.
а) Найдите длину отрезка АО, если известно, что диагональ АС = 12 см.
б) Чему равна диагональ BD, если известно, что отрезок ВО = 3 см?
в) Найдите периметр треугольника АОВ, если сторона АВ равна 7 см, а диагонали АС и BD равны 6 см и 10 см соответственно.
2. На чертеже изображены три параллелограмма с указанными данными. Найдите в них:
в) углы параллелограмма ТМНЕ.
Указание. Нужно спроектировать на экран задание 1 в) и чертежи задания 2 а), б), в).
МАТЕМАТИЧЕСКИЙ ДИКТАНТ № 2 . Свойства параллелограмма
1. Две стороны параллелограмма равны 3 см и 6 см. Найдите периметр параллелограмма.
2. Сумма двух противолежащих углов параллелограмма равна 86°. Чему равны эти углы?
3. Периметр параллелограмма равен 16 см. Одна из его сторон равна 5 см. Определите остальные стороны параллелограмма.
4. Найдите углы параллелограмма, если известно, что один из них равен сумме двух других углов параллелограмма.
5. Если одна из сторон параллелограмма равна 2,4 см, а вторая в 3 раза меньше, то периметр параллелограмма равен . . Закончите предложение.
МАТЕМАТИЧЕСКИЙ ДИКТАНТ № 3 . Виды параллелограммов
1. Является ли параллелограмм, у которого один угол прямой, прямоугольником?
2. Верно ли, что четырехугольник, у которого один угол прямой, является прямоугольником?
3. Верно ли, что любой прямоугольник является параллелограммом?
4. Может ли параллелограмм быть прямоугольником?
5. Диагонали четырехугольника равны. Верно ли, что этот четырехугольник — прямоугольник?
6. Диагонали параллелограмма равны 4 см и 5 см. Является ли этот параллелограмм прямоугольником?
7. Две соседние стороны параллелограмма равны и образуют прямой угол. Как называется этот параллелограмм?
МАТЕМАТИЧЕСКИЙ ДИКТАНТ № 4 . Трапеция
1. Изобразите горизонтальную прямую а и точки М и К, лежащие по одну сторону от этой прямой. Изобразите перпендикуляры МН и КТ к прямой а. Определите вид четырехугольника МКТН.
2. В трапеции проведены две высоты. Они разбили трапецию на два треугольника и четырехугольник. Определите вид этого четырехугольника.
3. В трапеции АВ — боковая сторона, ВН — высота, ВАН = 45°. Определите вид треугольника АВН.
4. Существует ли трапеция, при основании которой один угол острый, а другой — тупой? Если да, то изобразите такую трапецию.
5. Основания равнобедренной трапеции равны 12 и 8, а периметр равен 36. Найдите боковую сторону.
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.
🌟 Видео
Четырехугольники. Вебинар | МатематикаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

ГЕОМЕТРИЯ 8 класс: Четырехугольники | Видеоурок с теорией и решением задачиСкачать

ПРЯМОУГОЛЬНИК. §4 геометрия 8 классСкачать

Математика это не ИсламСкачать

ВСЯ ТЕОРИЯ по ГЕОМЕТРИИ ЗА 8 КЛАСС с примерамиСкачать

Как проверяют учеников перед ЕНТСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Детская задача про телевизоры Делаем домашнее задание по математикеСкачать

Как писать математический диктант?Скачать

Геометрия 8 класс за 1 час | Математика | УмскулСкачать

Геометрия 8 класс (Урок№1 - Многоугольники. Четырёхугольник.)Скачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Четырёхугольник и его элементы Геометрия 8клСкачать







