Треугольник в сечении куба (3 видео) | Курс школьной геометрии

Узнать ещё

Знание — сила. Познавательная информация

Содержание

Сечение куба плоскостью
«Сечение куба плоскостью и практическое их применение в задачах».
Методы построения сечений многогранников
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.
(система уроков и факультативных занятий по теме “Построение сечений многогранников”)
💡 Видео

Видео:Треугольник в сечении кубаСкачать

Сечение куба плоскостью

Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.

Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.

Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.

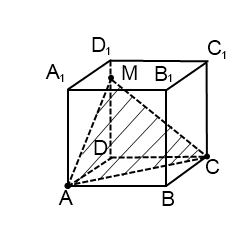
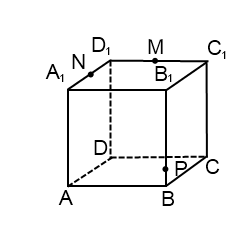
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.

Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.

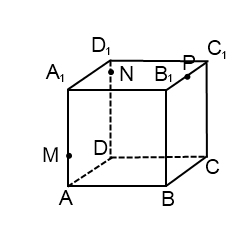
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.

Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).

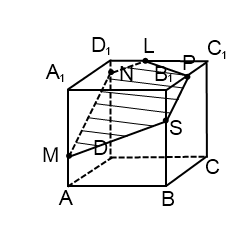
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).

Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.

Пятиугольник MNLPS — искомое сечение.

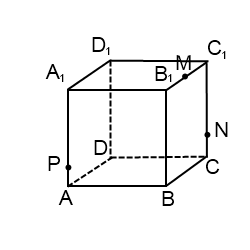
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.

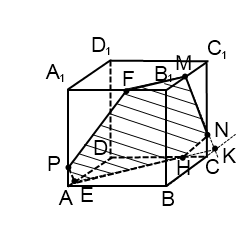
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).

Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.

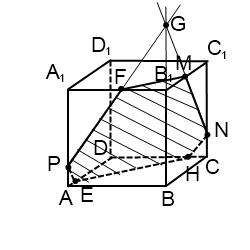
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).

Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.

Шестиугольник MNHEPF — искомое сечение.

Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.

Работа с прямой PE дает то же сечение MNHEPF.

4) Построить сечение куба плоскостью, проходящей через точку M, N, P.

Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.

Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.

Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.

Видео:Построение сечения куба по трем точкамСкачать

«Сечение куба плоскостью и практическое их применение в задачах».

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Общеобразовательная школа І-ІІІ ступеней №2

отдела образования администрации города Кировское

«Сечение куба плоскостью

и практическое их применение в задачах».

Подготовила учитель математики

Задачи на построение сечений многогранников занимают значительное место как школьном курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение этого вида задач способствует усвоению аксиом стереометрии, систематизации знаний и умений, развитию пространственного представления и конструктивных навыков. Общеизвестны трудности, возникающие при решении задач на построение сечений.

Основными действиями, составляющими метод построения сечений, являются нахождение точки пересечения прямой с плоскостью, построение линий пересечения двух плоскостей, построение прямой параллельной плоскости, построение прямой перпендикулярной плоскости.

Проиллюстрирую построение сечения на одной задаче из школьного курса математики:

Решение: Построим два требуемых сечения, взяв точку М₁ ближе к точке В, а точку М₂ближе к В₁. Оба сечения показаны на рисунке .В начале движения когда точка М₁только отошла от точки В₁, сечение представляет собой треугольник с основанием АС и высотой М₁О, которая чуть больше отрезка ВО, т.е. Если точка М₁ займёт положение М₂расположенной очень близко к точке В₁, то АМ₂С почти совпадёт с АВ₁С, а его высота М₁О – с отрезком В₁О, длина которого равна (ОВ₁==).

Отсюда по соображениям непрерывности делаем вывод:

Особо следует посмотреть, что произойдёт, если точка М₁ займёт положение вершины В.

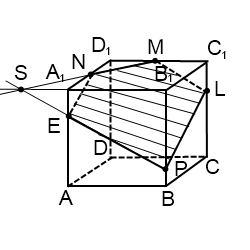
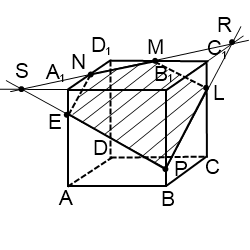
№2. Построить сечение куба плоскостью, проходящей через три точки А₁, E и L , лежащие на рёбрах куба.

Плоскости граней A ₁ ADD ₁ и DD ₁ C ₁ C пересекаются по прямой DD ₁, а плоскости граней A ₁ B ₁ C ₁ D ₁ u DD ₁ C ₁ C – по прямой D ₁ C ₁. Соединив точки А и Е , получим прямую пересечения секущей плоскости с плоскостью грани AA ₁ D ₁ D , а продолжив её, найдём точку N , принадлежащую трём плоскостям: плоскости сечения и плоскостям граней AA ₁ D ₁ D u DD ₁ C ₁ C .

Аналогично найдём точку М, общую трём плоскостям: плоскости сечения и плоскостям граней A ₁ B ₁ C ₁ D ₁ u DD ₁ C ₁ C . Таким образом, точки N u M принадлежат секущей плоскости и плоскости DD ₁ C ₁ C ; прямая MN – линия пересечения плоскости сечения с плоскостью грани DD ₁ C ₁ C , а F и K – точки пересечения её с рёбрами куба CD u CC ₁. Последовательно соединив прямыми точки A ₁, E , F , K u L , получаем пятиугольник A _! EFKL , который и даст нам искомое сечение.

При построении сечения куба плоскостью Х при произвольном расположении точек в сечении получается: треугольник, трапеция, прямоугольник, пятиугольник или шестиугольник. Естественно возник вопрос, как вид сечения зависит от вида расположения точек задающих это сечение

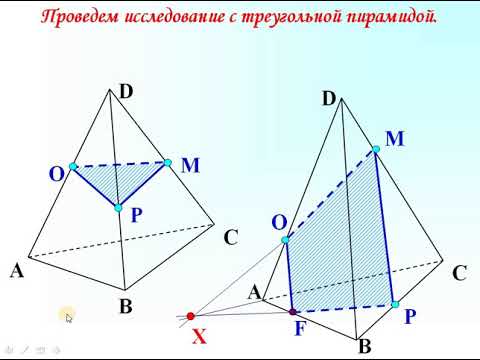
Я решил провести исследование, цель которого является выяснение.

Построить сечения куба плоскостью, когда заданы три точки принадлежащие рёбрам с одной вершиной.

Взяты три точки A ₁, D , C ₁, которые принадлежат вершине D ₁, а сами являются вершинами куба.

В сечении получился равносторонний треугольник, так как A ₁ C ₁, A ₁ D u DC ₁ – диагонали граней этого куба.

Три точки: A ₁ u C ₁ – вершины куба, а точка F принадлежит ребру куба DD ₁. Точки принадлежат прямым выходящим из вершины D ₁.

В сечении получился равнобедренный треугольник, так как F равноудалена от точек A ₁ u C ₁.

Три точки: A ₁ u C ₁ – вершины куба, а точка F принадлежит прямой ребра куба DD ₁. Точки принадлежат прямым выходящим из одной вершины D ₁.

В сечении получается равнобедренная трапеция, так как F равноудалена от точек A ₁ u C ₁, то есть LA ₁= KC ₁.

Три точки принадлежащие рёбрам с одной вершиной D ₁. Точки F u M принадлежат продолжениям рёбер D ₁ D u D ₁ C соответственно, а точка A ₁ является вершиной куба.

В сечении получился пятиугольник A ₁ KLNG .

Взяты три точки F , M u Q так, что лежат на продолжении рёбер D ₁ D , D ₁ C ₁, и D ₁ A ₁ соответственно.

В сечении получился шестиугольник KLNGJH .

Три точки лежат на рёбрах с одной вершиной D ₁.

В сечении получился произвольный треугольник, но если точки расположить так чтобы D ₁ Q = D ₁ M = D ₁ F , то есть если они были бы равноудалены от вершины D ₁ то в сечении получился бы равносторонний треугольник.

Секущая плоскость задана точками Н, Q и M . В сечении получается параллелограмм, так как KC ││ MP и MK ││ PC по теореме о пересечении двух параллельных плоскостей третьей.

Если точки H , Q и M , задают секущую плоскость, удаленные от D , на расстоянии 2 a , где а – для ребра куба, то в сечении получается правильный треугольник ACB ₁.

Вывод: три задающих сечение точки принадлежат трём рёбрам куба с общей вершиной или являются их продолжением, то в сечении получается: треугольник, пятиугольник, шестиугольник трапеция, параллелограмм.

Построение сечения куба плоскостью, когда заданы три точки, две из которых лежат на смежных рёбрах, а третья точка лежит на ребре не смежном с ними.

Три точки M , K u F , взяты так что M u F принадлежат рёбрам с одной вершиной A ₁, а точка K лежит на ребре не смежным с ними.

В сечении получается прямоугольник, так как А₁М= D ₁ K и по теореме о трёх перпендикулярах можно доказать что MKLF – прямоугольник., а если А₁М D ₁ K , то может получится трапеция или пятиугольник.

Взяты три точки так, что K u L принадлежат рёбрам выходящим из одной вершины A _1, а точка N принадлежит ребру CC ₁, не смежному сними. K , L u N середины рёбер A ₁ A , A ₁ B ₁ u CC ₁ – соответственно.

В сечении получается правильный шестиугольник KLGNHM

Взяты три точки так, что K u L принадлежат рёбрам выходящим из одной вершины A _1, а точка T принадлежит ребру DC .

В сечении получается шестиугольник KLFRTZ .

Три точки взяты так, что K u L принадлежат рёбрам куба с одной вершины A ₁, а точка M ребре DD ₁.

В сечении получается трапеция LKQM .

Три точки K u L которые принадлежат рёбрам с одной вершиной A ₁.и точка R которая лежит на ребре BC .

В сечении получается пятиугольник KLFRT .

Вывод: Если секущая плоскость задана тремя точками, две из которых лежат на смежных рёбрах, а третья на ребре не смежном с ними, то в сечении может получиться прямоугольник, пятиугольник, шестиугольник, трапеция.

В сечении куба параллелограмм и его частные случаи.

Точки T , H , J задающие сечение расположены так, что THAD , HJAD . В сечении получается квадрат HTKJ .

Сечение задано точками C , F , L , причём DF = FD ₁, BL = LB ₁. В сечении получается ромб AFCL .

Сечение задано точками C , G , H . B ₁ H = DG . В сечении параллелограмм A ₁ GCH.

Точки задающие сечение являются вершинами куба A , D , C ₁. В сечении получается прямоугольник

В сечении куба правильные многоугольники

Треугольник АВВ₁ равносторонний, так как его стороны это диагонали граней куба.

Треугольник КМТ равносторонний, так как КВ=МВ=ТВ.

КМТЕ – квадрат, так как сечение задано точками М, К, Е и МК AD , EKAD .

В сечении правильный шестиугольник КМТНЕО, так как точки Н, Е, К задающие сечение являются серединами рёбер СС₁, DC , АА₁ соответственно.

Куб и несколько задач по стереометрии с ЕГЭ.

В пособии “ЕГЭ 2005. Математика. Типовые тестовые задачи” (Корникова Т. А. и др.) Содержит 10 задач (С4) по стереометрии, объединенных общей идеей: дана треугольная призма АВСА ₁ В ₁ С ₁ стороны основания АВ и ВС взаимно перпендикулярны и перпендикулярны ребру ВВ ₁ , АВ=ВС=ВВ ₁ , вершина А является вершиной конуса (или центром одного из оснований цилиндра, или центром сферы), основание конуса (сфера или второе основание цилиндра) проходит через середину одного ребра призмы, длина его известна. Надо найти объем или поверхность конуса (сферы, цилиндра).

Общий пример решения:

Данную призму дополнить до куба. Шестиугольник DEFKLM – сечение куба плоскостью основания конуса , окружность которого проходит через середину А₁В₁, А – вершина конуса, или

DEFKLM – сечение куба плоскостью основания цилиндра, окружность которого проходит через середину А₁В₁, А – центр второго основания цилиндра, или это сечение куба плоскостью большого круга сферы с центром А, сфера которого проходит через середину А₁В₁.

Шестиугольник DEFKLM – сечение куба плоскостью, проходящей через середину рёбер А ₁ В ₁ , ВВ ₁ , ВСЖ при построении получаются точки K , L , M , которые являются серединами соответствующих рёбер. Стороны этого шестиугольника являются гипотенузами треугольников DB ₁ E , EBF , FCK , KQL , LRM , MA ₁ D , катеты которых равны половине ребра куба. Тогда центр этого шестиугольника является центром описанной около него окружности, которая пересекает рёбра куба в точках D , E , F , K , L и М, радиус этой окружности , где А ₁ В ₁ = а .

AO EL, т . к . EAL – равнобедренный: AL = AE .

( ABE u EAL – прямоугольные, AB = AQ = а, BE = LQ = )

EO = OL как середина диагонали Е L шестиугольника DEFKLM , т. е. АО – медиана ,а по свойствам равнобедренного треугольника и высота. Аналогично доказывается АО DK . Так как АО перпендикулярна к двум пересекающимся прямым плоскости шестиугольника, то АО перпендикулярна ко всей плоскости.

Если А – вершина конуса то АО – его высота, если А – центр второго основания цилиндра, то АО- высота цилиндра.

АВС: АС=, P – точки пресечения диагоналей основания куба, АР=, РР ₁ =АА ₁ = а . ОР=РР ₁ = , тогда из прямоугольного РОА АО=. И так АО=.

Тогда, если идёт речь о конусе:

(из ).

Ответ:

Корникова Т. А. и др. типовые тестовые задания. ЕГЭ – 2005

Задача. Даны призма АВСА₁В₁С₁ и цилиндр. Стороны АВ и ВС основания призмы перпендикулярны ребру ВВ₁ и взаимно перпендикулярны. Центром основания цилиндра служит точка А₁ окружность второго основания проходит через середину ребра А₁В₁.

Найдите площадь полной поверхности цилиндра, если ВВ₁=АВ=ВС=10. Найдите его объём.

. .

Так как стороны АВ и ВС основания призмы перпендикулярны ребру ВВ₁ и взаимно перпендикулярны и АВ=ВС=ВВ₁, то призма АВСА₁В₁С₁ – это половина куба с ребром АВ. Окружность второго основания цилиндра проходит через середину А₁В₁. Эта окружность пересекает и другие рёбра куба. И эти точки пересечения окружности второго основания цилиндра и рёбер куба лежит в одной плоскости (плоскость сечения) и равноудалены от центра второго основания цилиндра. Плоскость второго основания цилиндра образует в сечении куба шестиугольник DEFKLM , все вершины которого являются вершинами соответствующих рёбер. Тогда ED =АР= R , ЕВ₁ D , В=90 0 (по условию), B ₁ E = DB ₁=, тогда по теореме Пифагора ED =, R =.

Докажем, что АО перпендикулярно к сечению DEFKLM ,так как является его высотой цилиндра.

РОА , Р=90 0 РА=, РО=.

По теореме Пифагора ОА= (ОА= h =).

SPO, P=90 0 PS= SO

в AOS: AO 2 =75 SO 2 =

AS 2 =AO 2 +SO 2 . AOS – прямоугольный АО SO .

Ответ:

Корникова Т. А. и др. типовые тестовые задания. ЕГЭ – 2005

Задача. Даны призма АВСА₁В₁С₁ и конус. Стороны АВ и ВС основания перпендикулярны ребру ВВ₁ и взаимно перпендикулярны. Вершина конуса располагается в точке А, окружность основания проходит через середину ребра А₁В₁.

Найдите площадь полной поверхности конуса, если ВВ₁=АВ=ВС=8. Найдите объём этого конуса.

. .

Так как по условию дана прямая призма, в которой ВВ₁=АВ=ВС, то эта призма является половиной куба. Вершина куба А является и вершиной конуса, основание которого пересекает А₁В₁ в точке D , следовательно AD – образующая конуса AD =. Сечение куба плоскостью основания конуса – это правильный шестиугольник DEFKLM , т.к. А D , AE , AF , AK , AL , AM – это образующие конуса, вершины D , E , F , K , L , M – равноудалены от основания высоты конуса в точке О, являются серединами рёбер куба. R=ED, EB ₁ D, B ₁ D =B ₁ E=4, ED=4.

AA ₁ D, A ₁ =90 0 , AD=.

AC = (из ОАН, ОН АН, НО=4, АН=4).

Ответ:

В результате проведённого компьютерного эксперимента в работе было выявлено: что в зависимости от точек задающих секущую плоскость в сечении куба могут получиться треугольники (произвольный, равнобедренный и правильный), четырёхугольники (квадрат, прямоугольник, трапеция, ромб, параллелограмм), пятиугольники и шестиугольники. Особое выделены правильный треугольник и шестиугольник, рассмотрены свойства этих многоугольников и задачи с ними связанные располагавшиеся в одном из пособий для подготовки к ЕГЭ по математике.

Выполнение работы расширило мои представления о выполнении построений сечения многогранников плоскостью, дало возможность более глубоко освоить некоторые компьютерные программы способствующие развитию конструктивных навыков, которые позволили разобраться в решении задач по стереометрии, предлагающихся в ЕГЭ по математике.

Видео:Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnlineСкачать

Методы построения сечений многогранников

Разделы: Математика

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
В задачах используются в основном простейшие многогранники.
Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

что значит построить сечение многогранника плоскостью;
как могут располагаться относительно друг друга многогранник и плоскость;
как задается плоскость;
когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

тремя точками;
прямой и точкой;
двумя параллельными прямыми;
двумя пересекающимися прямыми,

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

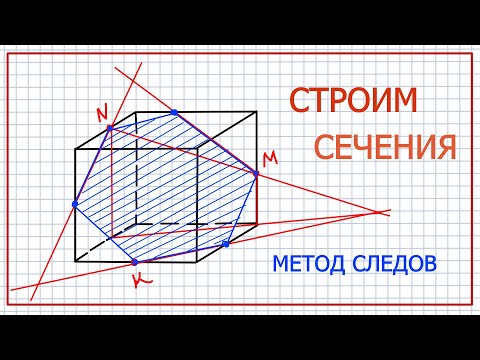
Метод следов.
Метод вспомогательных сечений.
Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:

Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
Погорелова А.В. (Геометрия, 7-11);
Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
Смирновой И.М. (Геометрия, 10-11);
Шарыгина И.Ф. (Геометрия, 10-11).

Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.

В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).

В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.

Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.

Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:

Определение сечения многогранников.
Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).