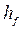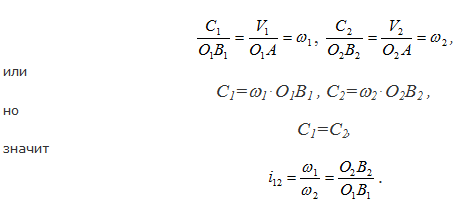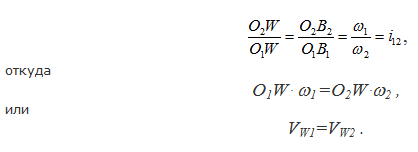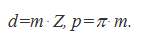Когда совпадают начальные и делительные окружности (7 видео)

Основы теории зубчатого зацепления

Меньшее зубчатое колесо называют шестерней, большее — колесом.

Параметрам шестерни приписывают индекс 1, параметрам колеса — индекс 2 (рис.16.8).

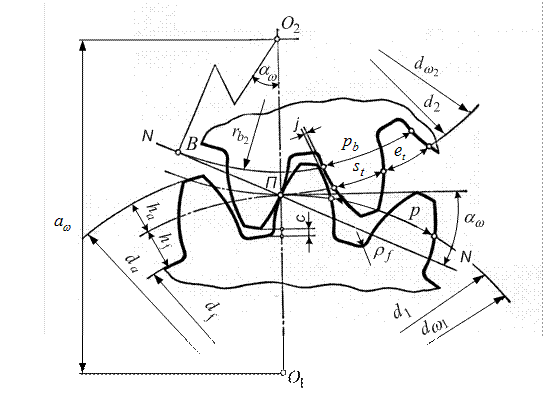
Точка П называется полюсом зацепления. Линия Т-Т — это касательная, проведенная к начальным окружностям. Линия N—N — это нормаль.

Рис. 16.8. Основные геометрические параметры эвольвентного зацепления

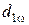
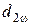
1. Начальные окружности — это окружности диаметром и , которые в процессе зацепления перекатываются одна по другой без скольжения.

При изменении межосевого расстояния 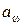меняются и диаметры начальных окружностей.

У отдельно взятого колеса начальной окружности не существует, поэтому ее нельзя принять за базу для определения параметров зубчатой передачи.

2. Делительные окружности — это окружности диаметрами d, по которым обкатывается инструмент при нарезании зубьев (рис. 16.8).

Делительная окружность принадлежит отдельно взятому колесу.

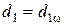
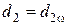
У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают ; . Исключение составляют передачи с угловой коррекцией.

3. Межосевое расстояние

. (16.1)

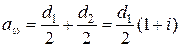
4. Окружной шаг зубьев p — это расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности.

, (16.2)

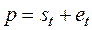
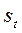
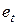
где — толщина зуба по делительной окружности; — ширина впадины по делительной окружности.

Для пары сцепляющихся колес окружной шаг должен быть одинаковым.

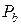
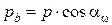
Основной шаг измеряется по основной окружности

, (16.3)

где 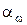— угол зацепления, т. е. угол между нормалью N—N и касательной Т—Т.

5. Окружной модуль зубьев

Модулем зубьев m называется часть диаметра делительной окружности, приходящейся на один зуб.

Полная длина делительной окружности зубчатого колеса:

, (16.4)

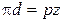
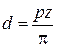
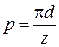
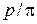
где z — число зубьев; или , число p является трансцендентным, что неудобно при изготовлении или расчете зубчатых колес. Поэтому в качестве основного расчетного параметра принято рациональное число , которое обозначается буквой m (мм) и называется модулем зубьев. Для пары зацепляющихся колес модуль одинаков. Модулем называется часть диаметра делительной окружности, приходящейся на один зуб.

6. Высота головки и ножки зуба

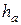
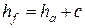
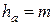
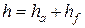
Начальная окружность делит зуб по высоте на головку и ножку

; ; , (16.5)

где с — радиальный зазор.

7. Дугой зацепления s называется путь, проходимый профилем зуба по начальной окружности за время фактического его зацепления.

Для обеспечения непрерывности зацепления:

Коэффициент перекрытия для плавности и непрерывности зацепления должен выполнять условие

. (16.7)

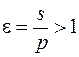
8. Передаточное отношение:

. (16.8)

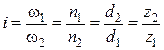
Существует понятие передаточного числа:

. (16.9)

Содержание

Детали машин
Геометрические параметры эвольвентного зацепления
Начальные окружности
Делительная окружность
Окружной шаг зубьев
Основной шаг
Окружная толщина зуба и окружная ширина впадины
Окружной модуль зубьев
Высота головки и ножки зуба
Длина активной линии зацепления
Коэффициент торцового перекрытия
iSopromat.ru
Элементы зубчатого зацепления
📺 Видео

Видео:Модуль шестерни и параметры зубчатого колесаСкачать

Детали машин

Видео:Зубонарезание для чайников за 6 минут. Часть I - теорияСкачать

Геометрические параметры эвольвентного зацепления

Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.

В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:

w – начальной;
b – основной;
a – вершин зубьев;
f – впадин зубьев.

Параметрам, относящимся к делительной окружности, индекс не присваивается.

При обозначении параметров пары зубчатых колес индекс «1» присваивается шестерне, «2» — колесу.

Начальные окружности

Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О₁ и О₂ до полюса П ) при неизменном межосевом расстоянии О₁О₂ тоже остается неизменным.
При изменении межосевого расстояния a_w меняются и диаметры d_w начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.

Межосевое расстояние определяется по формуле:

Делительная окружность

Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.

Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.

У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:

Исключение составляют передачи с угловой модификацией.

Окружной шаг зубьев

Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.

Основной шаг

Этот параметр, обозначаемый p_b , относится к основной окружности. На основании второго и четвертого свойств эвольвенты расстояние по нормали между одноименными сторонами двух соседних зубьев равно шагу p_b .
Из треугольника О₂ВП (см. рис. 1) диаметр основной окружности d_b2 = 2 r_b2 = d₂ cos α_w , откуда основной шаг может быть определен по формуле:

Окружная толщина зуба и окружная ширина впадины

Окружная толщина зуба s_t и окружная ширина впадины e_t по дуге делительной окружности колеса передачи без смещения теоретически равны. Однако при изготовлении зубчатых колес на теоретический размер s_t назначают такое расположение поля допуска, при котором зуб получается тоньше, чем и гарантируется боковой зазор j (рис. 1), необходимый для нормального зацепления. По делительной окружности всегда s_t + e_t = p .

Окружной модуль зубьев

Из определения окружного шага следует, что длина делительной окружности зубчатого колеса πd = pz , где z – число зубьев. Следовательно,

Шаг зубьев p , так же как длина окружности, включает в себя трансцендентное число π , а поэтом шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число p/π , которое называют модулем зубьев , обозначают m и измеряют в миллиметрах:

d = mz или m = d/z .

Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.

Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).

При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.

Высота головки и ножки зуба

Делительная окружность делит зуб по высоте на головку h_a и ножку h_f . Для создания радиального зазора с (см . рис. 1) необходимо

Для передачи без смещения h_a = m .

Длина активной линии зацепления

При вращении зубчатых колес точка зацепления S (см. рис. 1) пары зубьев перемещается по линии зацепления NN . Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S» пересечения линии зацепления с окружностью вершин шестерни.
Отрезок S’S» линии зацепления называют длиной активной линии зацепления и обозначают g_α . Длину g_α легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S» и замеряют g_α .

Коэффициент торцового перекрытия

Коэффициентом торцового перекрытия ε_α называют отношение длины активной линии зацепления к основному шагу:

где z₁ и z₂ – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.

Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.

За период работ пары зубьев точка их зацепления проходит путь, равный по длине g_α (см. рис. 1), а расстояние между профилями соседних зубьев по линии зацепления равно основному шагу p_b . При g_α > p_b необходимое перекрытие зубьев обеспечивается.

По условию непрерывности зацепления должно быть ε_α > 1. С увеличением количества зубьев z увеличивается и коэффициент торцового перекрытия ε_α .

Видео:Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

iSopromat.ru

Основной закон зацепления профилей зубьев колес зубчатых передач гласит: для нормальной безотрывной работы передачи, составленной из двух профилей, входящих в высшую кинематическую пару, необходимо, чтобы нормаль к этим профилям в точке контакта в любой момент времени проходила через мгновенный центр их относительного вращения.

Зубья зубчатых колес составляют высшую пару IV класса, т.е. представляют собой некоторые поверхности, находящиеся в контакте.

Таким образом, профили зубьев – это кривые (а в некоторых случаях прямые) линии.

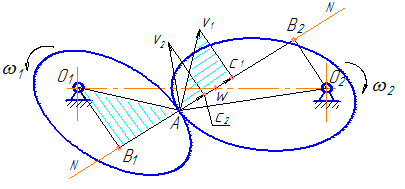
На рисунке 34 показаны два профиля, находящиеся в контакте в точке А. Скорость точки А, принадлежащей первому профилю (V₁), перпендикулярна радиусу О₁А, соответственно, скорость точки А, принадлежащей второму профилю (V₂), перпендикулярна радиусу О₂А.

Рассмотрим проекции этих скоростей на общую нормаль (N-N), проведенную к профилям в точке их контакта (С₁ – проекция скорости V₁ , С₂ – проекция скорости V₂). Могут получиться различные соотношения между значениями этих проекций:

С₂ > С₁ – точка А, принадлежащая второму профилю (А₂), в направлении нормали движется быстрее точки А, принадлежащей первому профилю (А₁). Второй профиль «убегает» от первого, в следующий момент произойдет разрыв кинематической пары (нарушится контакт между звеньями);
С₁ > С₂ – точка А₁ в направлении нормали движется быстрее точки А₂ (положение на рисунке 34 соответствует этому случаю), то есть точка А₁ стремится к внедрению во второй профиль. Если вычертить следующее положение механизма, то первый профиль в области точки А будет накладываться на второй.
В теории зацепления это явление носит название «интерференция профилей». В реальном механизме это приведет к заклиниванию или поломке передачи. Очевидно, что оба этих положения недопустимы – и разрыв кинематической пары, и, тем более, заклинивание и поломка делают передачу неработоспособной;
С₁ = С₂ – условие нормальной безотрывной работы профилей.

Из рисунка 34 видно, что ΔAV₁C₁ подобен ΔO₁AB₁ , и, соответственно, ΔAV₂C₂ подобен ΔO₂AB₂ . Из подобия треугольников можно записать отношение сходственных сторон:

Здесь i₁₂ – передаточное отношение от первого профиля ко второму (это отношение угловой скорости на входе к угловой скорости на выходе).

Из подобия треугольников O₁B₁W и O₂B₂W (W – точка пересечения общей нормали N-N с линией центров O₁O₂) получаем:

V_W1 – скорость точки W, связанной с первым профилем,
V_W2 – скорость точки W, связанной со вторым профилем.

Эти скорости совпадают не только по величине, но и по направлению (V_W1 ⊥ O₁W, V_W2 ⊥ O₂W, т.е. оба вектора перпендикулярны межосевому расстоянию O₁O₂).

Две точки совпадают по своему положению и имеют одинаковые скорости, то есть их относительная скорость равна нулю (V_W1W2=0). Таким образом, точка W является мгновенным центром относительного вращения рассматриваемых профилей.

Исходя из вышеизложенного, можно следующим образом сформулировать условие работоспособности передачи, составленной из двух профилей, входящих в высшую кинематическую пару:

— для нормальной безотрывной работы профилей необходимо, чтобы нормаль к этим профилям в точке контакта в любой момент времени проходила через мгновенный центр их относительного вращения.
Это условие носит название основного закона зацепления.

Профили, удовлетворяющие основному закону зацепления, называются сопряженными, а кривые которыми они описаны являются взаимоогибаемыми кривыми. При работе передачи взаимоогибаемые кривые перекатываются друг по другу со скольжением. Геометрическое место мгновенных центров скоростей, связанных с первым и вторым колесами, являются центроидами.

При работе передачи центроиды касаются в мгновенном центре относительного вращения и перекатываются друг по другу без скольжения. При постоянном передаточном отношении центроиды представляют собой окружности, которые в теории зацепления называются начальными окружностями.

Таким образом, передачи с постоянным передаточным отношением – это передачи с круглыми колесами, которые используются в большинстве случаев практики. В этом случае мгновенный центр при работе передачи не меняет своего положения и называется полюсом зацепления.

Видео:Деление окружностиСкачать

Элементы зубчатого зацепления

Стандартами на зубчатое зацепление вводятся определенные обозначения параметров:

Z – число зубьев колеса;
d – диаметр;
h – высота;
p – шаг (расстояние между одноименными профилями зубьев, измеренное по дуге какой-либо окружности);
S – толщина зуба (также измеряется по дуге окружности);
e – ширина впадины между зубьями;
a – межосевое расстояние.
Вводятся также буквенные индексы, показывающие, к какой окружности относится параметр:
w – начальная окружность;
b (или B) – основная окружность;
a – окружность вершин;
f – окружность впадин;
Y – окружность произвольного радиуса;

Без буквенного индекса – делительная окружность. Делительная окружность – это окружность, на которой шаг (и угол профиля) является стандартным:

Как видно из формул, вносить в стандарт непосредственно значения шага неудобно, т.к. при этом диаметр делительной окружности всегда будет величиной иррациональной (при изготовлении круглых деталей измеряют диаметры, поэтому надо, чтобы именно диаметры имели удобную величину). Поэтому в стандарт вводится величина, характеризующая отношение шага к числу π , которая называется модулем зацепления ( обозначается «m» и представлена в стандарте в миллиметрах).

Таким образом, основные параметры делительной окружности определяются следующими формулами:

Модуль зацепления, с одной стороны обеспечивает условие взаимозаменяемости колес (работать в паре могут любые колеса одного модуля), с другой стороны определяет область применения зубчатых передач (передачи с m
Курсовой проект по ТММ >

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах